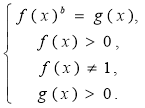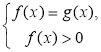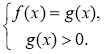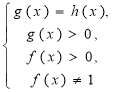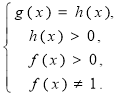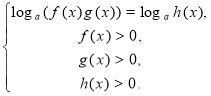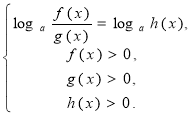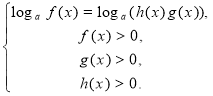Логарифмічні рівняння

 

Львівський техніко-економічний коледж НУ “Львівська політехніка“

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СЦЕНАРІЙ

Відкритого заняття з математики на тему

“Розв’язування

логарифмічних

рівнянь”

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Викладач: Сулик Н.Я.

 

 

 

 

 

 

 

 

 

Львів –2015

 

 

Розглянуто   і   схвалено

       на засіданні циклової комісії

                                                          природничо-математичних

            дисциплін

 

Протокол  №___ від ___________ 2015 р.

   

Голова комісії             Давидова О.В.

 

 

 

Зміст

 

1. Тема і мета заняття          3
2. Організаційна частина          3
3. Актуалізація опорних знань        3
4. Мотивація навчальної діяльності       4
5. План основної частини заняття
   1. Пояснення правил групової роботи та її оцінювання    4
   2.  Формування знань і вмінь         5
   3. Застосування знань і вмінь        5
6. Закріплення нового матеріалу        5
7. Підсумок заняття          6
8. Приклади розв’язування логарифмічних рівнянь і завдання для  індивідуального виконання у першому складі групі.
   1. Додатки 1.1-1.2 – Розв’язування логарифмічних рівнянь за означенням логарифма.                                                                                                                                            7
   2. Додаток 1.3 – Розв’язування логарифмічних рівнянь за методом потенціюванння.                                                                                                                                            8
   3. Додаток 1.4 – Розв’язування логарифмічних рівнянь за методом потенціюванння з використанням властивостей логарифма.                            9
9. Додаток 1.5 – Приклад розв’язування логарифмічних рівнянь за методом переходу до однієї основи для додаткового завдання.                                                        11
10. Додаток 2 – Завдання для самостійної роботи у другому складі групи. 12
11. Додаток 3 – Бланк відповіді        13
12. Додаток 4 – Загальна схема розв’язування логарифмічних рівнянь  14

Тема: «Розв’язування логарифмічних рівнянь»

 

Мета заняття:

навчальна ознайомити студентів із загальною схемою розв’язування логарифмічних рівнянь різних типів; формувати вміння використовувати різні методи розв’язування рівнянь і вибирати раціональніший із них визначаючи тип рівняння.

виховна вдосконалювати навички математичної мови студентів, виховувати вміння працювати в колективі, розвивати зацікавленість до предмету, працелюбність, увагу, пам’ять, сприяти розвитку уміння перемагати над труднощами навчаючись самому і в групі.

 

 

Організаційна частина

Перевірка готовності аудиторії та присутності студентів.

 Парти в аудиторії зсунуті по дві, щоби можна було працювати групами, на кожній парі парт проставлені номери груп 1,2,3,4. Студенти сидять по 4-5 чоловік.

 

Слово привітання. Прошу повідомити хто відсутній на парі?

 

 

Перевірка домашнього завдання

На попередньому занятті ми з вами познайомилися з показниковими рівняннями і навчилися розв’язувати їх використовуючи різні методи.

Чи всі завдання вдалося виконати вдома самостійно?

Які труднощі у вас виникли при виконанні домашнього завдання?

 

Викладач відповідає на запитання, що виникли у студентів під час виконання домашнього завдання або пропонує іншим студентам пояснити необхідне завдання.

 

Актуалізація опорних знань

 

У формі фронтальної бесіди пригадуємо основні поняття, необхідні для розглядуваної теми.

 

1. Що таке рівняння?
2. Що означає розв’язати рівняння?
3. Яке рівняння називається показникових?
4. Як розв’язати найпростіше показникове рівняння?
5. Як пов’язані між собою показникова і логарифмічна функції?
6. Яка область визначення логарифмічної функції?
7. Яка область значень логарифмічної функції?
8. На що треба звертати увагу, при порівнянні показникових та логарифмічних функцій?

 

Мотивація навчальної діяльності
(повідомлення теми, формування мети та основних завдань)

 

Використання рівнянь в повсякденному житті – рідкість. Вони знайшли своє застосування в багатьох галузях господарства і практично в усіх новітніх технологіях.

• Відомо, що, консервуючи овочі, важливо знати кислотність розчину, а знаючи кислотність, можна визначати концентрацію іонів водню. Це можна зробити за допомогою логарифмічних рівнянь, використовуючи логарифм з основою 10.

 

•               Теорія музики : щоби відповісти на питання на скільки частин треба розбити октаву треба визначити раціональне наближення для числа 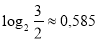. Якщо розкласти це число у неперервний дріб, тоді переконуємося, що найбільше підходить третій дріб 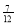, який і зумовлює класичний поділ октави на 12 півтонів.

 

 

План основної частини заняття

 

1. Пояснення правил групової роботи та її оцінювання.

 

На попередніх заняттях ми з вами навчилися працювати у малих групах, з використанням відтворювально-консультативного методу навчання.

 

Сьогодні ми продовжимо працювати у малих групах, а також спробуємо використати принцип «навчаючи – навчаюсь»:

 

1.1. Кожна група отримала один із методів розв’язування логарифмічних рівнянь і приклади його використання.

Вам необхідно розібрати запропонований метод за зразком і розв’язати цим методом два рівняння.

 

1.2. Далі формуємо нові групи, по одному учаснику з кожної із попередніх груп. Студенти вибирають один із варіантів завдань для самостійної роботи і обмінюючись досвідом розв’язують чотири запропоновані рівняння.

 

Отримані відповіді записують у спеціальний бланк (додаток 2).

 

1.3. Оцінка за роботу на занятті складається таким чином: 2 бали робота в І-ій групі, +4 бали робота в ІІ-ій групі, +3 бали правильність виконання роботи іншими учасниками ІІ-ої групи (робота консультанта), +2 бали за виконання додаткового 5-го завдання, +1додатковий бал отримує група, що справилася першою.

 

 

 

2. Формування знань і вмінь у вивченні нових методів розв’язування логарифмічних рівнянь. 

 

• У малих групах по 4-5 чоловік студенти знайомляться із запропонованим методом розв’язування логарифмічних рівнянь і переписують приклади в зошит.

 

Далі кожний учасник групи вибирає і розв’язує два рівняння за розглядуваним методом. (Завдання для роботи у групах додаток 1.1–1.4).

Викладач контролює і при потребі консультує роботу студентів.

Студенти підписують і заповнюють спеціальний бланк відповіді (додаток 2).

 

Результат – розв’язок рівнянь визначає номер нової групи цього учасника, яку формують студенти на наступному етапі роботи. (Якщо у групі є 5 чоловік, тоді студенти, з №5 залишаються на своїх місцях.)

 

• Далі студенти перерозподіляються у нові групи, де отримують завдання, для самостійного виконання. (Студенти міняються місцями.)

 

• Утворилися нові малі групи по 4 чоловіки, в кожній з яких є по одному учаснику, що вивчав різні методи розв’язування логарифмічних рівнянь.

 

3. Застосування знань і вмінь у вивченні нових методів розв’язування логарифмічних рівнянь. 

Студентам пропонується розв’язати 5 логарифмічних рівнянь:

 

• 4 рівняння з використанням різних методів, які розглядалися в попередніх малих групах, і з кожним із яких знайомився один з учасників нової малої групи; студенти консультуються, і допомагають один одному розібратися і з запропонованими завданнями. (Завдання для самостійної роботи Додаток 2).

 

Отримані результати записують у бланк відповіді.

 

• П’яте рівняння додатково пропонується розв’язати за методом, описаним в опорному конспекті.

 

Закріплення нового матеріалу

 

Отже, ви мали можливість познайомитися на занятті з логарифмічними рівняннями і різними методами їх розв’язування, навчитися працювати в групах, консультувати і слухати консультанта.

Прошу назвати основні методи розв’язування логарифмічних рівнянь, з якими ви працювали:

• Означення логарифма;
• Потенціювання обох частин рівняння;
• Використання властивостей логарифма;
• Перетворення основи логарифма.

Загальну схему основних методів прошу вклеїти в зошит (додається кожному).

Підсумок заняття 

Оскільки ви сьогодні працювали і самостійно і групами, то й оцінювання вашої роботи буде комплексним, і залежатиме також від результатів групової роботи.

 

Студенти здають свої бланки відповіді.

 

Результати дізнаєтеся на наступному занятті.

 

Завдання додому (в т.ч. видача завдань для самостійної індивідуальної роботи)

 

[1] §5 ст.37-38 №№ 171,174.

Додаток 1.1

 

Приклади розв’язування логарифмічних рівнянь за означенням логарифма.

 

1. log₂(x–3)=4

   за означенням логарифма маємо: х–3=2⁴;

     х–3=16;

     х=19.

2. log₃(4x+7)=2

  4х+7 = 3²;

  4х=9–7;

  х=2/4=0,5.

Розв’язати самостійно (завдання для групи 1):

1. log₃(5x+4)=2
2. log₅(2x+3)=1
3. log₃(4x+1)=2
4. log₂(5x+6)=4
5. log₄(3x+7)=2
6. log₃(7x+6)=3
7. log₂(3x–4)=3
8. log₄(5x–4)=2
9. log₃(2x–1)=2
10. log₈(x+3)=1

 

 

 

Додаток 1.2

 

Приклади розв’язування логарифмічних рівнянь за означенням логарифма.

 

1. log_х(2х²-3x-4)=2

    Замінимо це рівняння рівносильною системою за схемою 2):

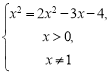
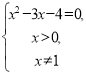
  х=4.

Відповідь: х=4.

При розв’язуванні рівнянь такого виду слід враховувати властивості основи логарифмічної функції, оскільки невідома х міститься не лише під знаком логарифма, а й в його основі.

 

2. log_х+3(2х²–3x–1)=2

 

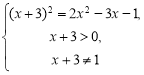
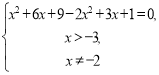
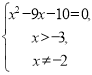
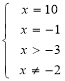х₁=10, х₂= –1.

Відповідь: х₁=10, х₂= –1.

 

Розв’язати самостійно (завдання для групи 2):

1. lоg_х+3(х²+3x+12)=2
2. log_х+1(х²–x+4)=2
3. log_х(х³+x–2)=3
4. log_х+1(х²–3x+11)=2
5. log_х–1(х²+3x–14)=2
6. log_2х+7(х²+4)=1
7. log_х+2(х²+2х+12)=2
8. log_х(х³+3x–12)=3
9. log_х–1(x+11)=2
10. log_5+х(х²+15х)=2

 

 

 

 

Додаток 1.3

 

Приклади розв’язування логарифмічних рівнянь за методом потенціювання.

 

1. log₃(4x–5)= log₃(7+3x).

 Замінимо рівняння рівносильною системою за схемою 3):

.

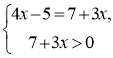
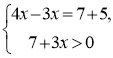
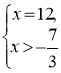Виберемо ті корені, які задовольняють умову:.

Відповідь: х=12.

 

2. log₃(х²–4x–5)= log₃(7–3x).

 Замінимо рівняння рівносильною системою за схемою 3):



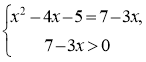
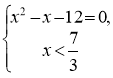
 Розв’яжемо квадратне рівняння:  х²–x–12=0

     х₁=4, х₂= –3.

 Виберемо ті корені, які задовольняють умову:

Відповідь: х=−3.

 

Розв’язати самостійно (завдання для групи 3):

1. lоg₃(3x+5)=lоg₃(2x+6)
2. lоg₂(6x–5)=lоg₂(2x–1)
3. lоg₄(2x–3)=lоg₄(3x–5)
4. lоg₃(2x+5)=lоg₃(4x+1)
5. lоg₂(7x–1)=lоg₂(4x+8)
6. lоg₇(2x+5)=lоg₇(3x+2)
7. lоg₂(x+5)=lоg₂(2x+1)
8. lоg₃(2x–7)=lоg₃(x–3)
9. lоg₂(7x+3)=lоg₂(6x+8)
10. lоg₃(2x+1)=lоg₃(5x–14)

 

Додаток 1.4

 

Приклади розв’язування логарифмічних рівнянь за методом потенціювання з використанням властивостей логарифма.

 

1. lg (x-9)+lg 2= lg (x+5).

    Суму логарифмів замінимо логарифмом добутку виразів:

    lg (2·(x-9))= lg(х+5)

    Замінимо рівняння рівносильною системою, враховуючи ОДЗ:

    Одержимо: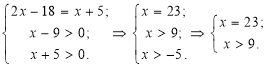 

Відповідь: х=23.

 

2. lg (x-9)+lg (2x-1)=2.

    Зобразимо число 2 у вигляді десяткового логарифма: 2=lg100

    lg (x-9)+lg (2x-1)=lg100

    Суму логарифмів замінимо логарифмом добутку виразів:

    lg (x-9)(2x-1)= lg100

    Замінимо рівняння рівносильною системою, враховуючи ОДЗ:

    Одержимо: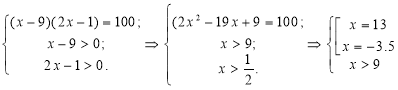 

    Виберемо ті корені, які задовольняють умову:.

 

Відповідь: х=13.

 

Розв’язати самостійно (завдання для групи 4):

1. lg(x+2)+lg3=lg(x+8)
2. lоg₈(x+1)+lоg₈(x+3)=1
3. lоg₂(x+1)+lоg₂(x–1)=lоg₂3
4. lоg₄(x–1)+lоg₄(x+2)=1
5. lоg₃(x–2)+lоg₃5=lоg₃(х+2)
6. lоg₂(x+1)+lоg₂(x–2)=2
7. lоg₂(x+8)=lоg₂(x–1)+2
8. lg(x+6)+lg2=lg(3x+8)
9. lоg₂(5x+7)=3+lоg₂(x–1)
10. lоg₈(x–1)+lоg₈(x–3)=1

Додаток 1.5

 

Приклади розв’язування логарифмічних рівнянь за методом зведення логарифмічного рівняння до однієї основи.

1.

     Зведемо всі логарифми до основи 2: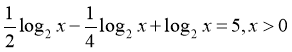      

     Зведемо подібні доданки: ; log₂ x = 4;  x = 2⁴. 

Відповідь: x=16.

 

Розв’язати самостійно:

 

1. log₂ x + 2log₄ x + 3log₈ x=9; 
2. .

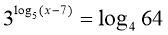Додаток 2

 

 

Розв’язати самостійно, використовуючи раніше описані методи:

 

Варіант 1:

1.         log₅(2x–7)=1
2.         lоg_х+2(х²–6x+14)=2
3.         lоg₃(2x+11)=lоg₃(4x–9)
4.         lоg₂(x+2)=lоg₂3+lоg₂(x–6)

5*. 2lоg₄(4–x)=4–lоg₂(–2–х)

 

 

Варіант 2:

1.         log₂(7x–10)=5
2.         lоg_х+1(х²–3x+6)=2
3.         lоg₄(5x–2)=lоg₄(3x+14)
4.         lоg₂(x–3)+3=lоg₂(3x+1)

5*. lоg₃(4–x)+lоg₉(2–х)²=1

 

 

Варіант 3:

1.         log₃(4x–7)=2
2.         lоg_х+2(х²+5x–7)=2
3.         lоg₄(3x–2)=lоg₄(2x+7)
4.         lоg₅(x+3)+lоg₅2=lоg₅(x+7)

5*. 2lоg₇(x–2)=lоg₇(х–10)²–2

 

 

Варіант 4:

1.         log₆(5x+1)=2
2.         lоg_х–1(х²+6x–15)=2
3.         lоg₂(3x+7)=lоg₂(4x–2)
4.         lоg₃(2x–5)=lоg₃(3–4x)+1

5*. lоg₃x–2lоgх=6

 

Варіант 5:

 

1. log₃(5x+1)=2
2. lоg_х–2(х²+7x–15)=2
3. lоg₅(6x+15)=lоg₅(9x–2)
4. lоg₂(2x–5)=lоg₂(3–4x)+1

5*. lоg₄x–2lоg_0,25х=6

 

 

Додаток 3

 

 

 

Бланк відповіді студента    _______________________________    Група Б12

Робота в І-ій групі		Робота в другій групі Група №          Варіант №					Робота консультанта			Додатковий бал групи	Сумарний бал студента
№1	№2	№1	№2	№3	№4	№5	1-й ст.	2-й ст.	3-й ст.
Впишіть відповіді до рівнянь за номером

 

 

 

 

Додаток 4

 

Логарифмічні рівняння

 

Логарифмічними називають рівняння які містять невідоме під знаком логарифма. Наприклад, log₂(3х-2)=4; lg(x-9)=1; lgx =4.

 

Розв’язування логарифмічних рівнянь ґрунтується на означенні логарифма, властивостях логарифмічної функції та властивостях логарифма.

 

 

Основні методи розв’язування логарифмічних рівнянь:

1) log a  f(x) = b             f(x)= a b     a>0;    a1.

2) log f(x)  g(x) = b    

3) log a  f(x) = log a  g(x)          або

4) log f(x)  g(x) = log f(x)  h(x)    або

5) loga  f(x)+ loga  g(x)=loga  h(x)

6) loga f(x)−loga g(x)=loga h(x)або

7) n log a  f(x) = log a  g(x)          

loga (f(x)g(x))= loga |f(x)|+ loga |g(x)| loga (f(x))2n = 2nloga |f(x)|