Підсумкова контрольна робота
ПІДСУМКОВА КОНТРОЛЬНА РОБОТА З МАТЕМАТИКИ
Варіант 1
1.1. Яка з даних функцій не є лінійною?
А) у=7х+3; Б) у=![]() ; В) у=
; В) у=![]() ; Г) у=
; Г) у=![]() .
.
1.2. Спростити вираз ![]() .
.
А) ctg2α; Б) tg2α; В) 1; Г) 1.
1.3. Знайти корені рівняння sin 4x = –1.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.4. Знайти корінь рівняння ![]() .
.
А) 6; Б) 4; В) 26; Г) 27.
1.5. Розв’язати нерівність ![]() .
.
А) (6;∞); Б) (-∞;6); В) (0;6); Г) (0;6)ᴗ(6;∞).
1.6. З натуральних чисел від 1 до 18 включно учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 18?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.7. Знайти похідну функції ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.8. Обчислити інтеграл ![]() .
.
А) 4; Б) ![]() ; В) 20; Г) 20,5.
; В) 20; Г) 20,5.
1.9. Знайти координати вектора ![]() , якщо
, якщо ![]() і
і ![]() (4;-2;0).
(4;-2;0).
А) ![]() (-2;1;0) ; Б)
(-2;1;0) ; Б) ![]() (-2;-1;0); В)
(-2;-1;0); В) ![]() (2;-1;0); Г)
(2;-1;0); Г) ![]() (2;1;0).
(2;1;0).
1.10. Висота конуса дорівнює 9 см, а його об’єм дорівнює 6 см3. Чому дорівнює площа основи конуса?
А) 2 см2 ; Б) 2 см2; В) 3 см2; Г) 6 см2.
2.1. Установити відповідність між виразами (1–4) та рівними їм степенями з дробовими показниками (А–Д):
1. ![]() А
А ![]()
2. ![]() Б
Б ![]()
3. ![]() В
В ![]()
4. ![]() Г
Г ![]()
Д ![]()
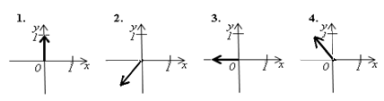 2.2. Установити відповідність між векторами, зображеними на рисунках (1–4) та їхніми можливими координатами (А–Д):
2.2. Установити відповідність між векторами, зображеними на рисунках (1–4) та їхніми можливими координатами (А–Д):
А (–1;0)
Б (0;1)
В (–1;1)
Г (1;–1)
Д (–1;–1)
3.1. Розв’язати рівняння: ![]() .
.
3.2. З точки А до площини α проведено дві похилі АВ і АС, довжини яких 15 см і 20 см відповідно. Знайти відстань від точки А до площини α, якщо проекції похилих на цю площину відносяться як 9:16.
Варіант 2
1.1. Подати у вигляді степеня вираз ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.2. Розв’язати рівняння tg 4x = ![]() .
.
А) ![]() ; В)
; В) ![]() ;
;
Б) ![]() ; Г)
; Г) ![]() .
.
1.3. Знайти корінь рівняння ![]() .
.
А) 1 ; Б) –5 ; В) –3 ; Г) 9.
1.4. Обчислити значення виразу lg 25 + lg 4.
А) 100 ; Б) lg 29 ; В) 2 ; Г)10.
1.5. Розв’язати нерівність 6х![]() .
.
А) [1; ∞); Б) (∞;1]; В) (∞;1]; Г) [1; ∞).
1.6. Знайти похідну функції y=ex sin x.
А) ![]() ex соs x.; В)
ex соs x.; В) ![]() ex (sin x – соs x);
ex (sin x – соs x);
Б) ![]() ex (sin x + соs x); Г)
ex (sin x + соs x); Г) ![]() xex–1 соs x.
xex–1 соs x.
1.7. Вказати первісну функції f(x)=8х3, графік якої проходить через точку А(1;2).
А) F(x)=2x4; Б) F(x)=24x222; В) F(x)=2x41; Г) F(x)=x4+1.
1.8. Скільки чотирицифрових чисел з різними цифрами можна записати, використовуючи цифри 0, 1, 2, 3?
А) 24; Б) 18; В) 20; Г) 16.
 1.9. Дано точки А(1;6;4), В(3;2;5), С(0;1;1), D(2;5;2). Яке з тверджень є правильним?
1.9. Дано точки А(1;6;4), В(3;2;5), С(0;1;1), D(2;5;2). Яке з тверджень є правильним?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
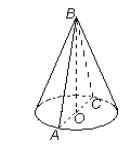
1.10. Висота конуса, зображеного на рисунку, дорівнює 14 см, а кут
при вершині осьового перерізу = 1200. Знайти радіус основи конуса.
А) 14![]() см; Б)
см; Б) ![]() см; В) 7
см; В) 7![]() см; Г) 7 см.
см; Г) 7 см.
2.1. Установити відповідність між відсотками (1–4) та десятковими дробами (А–Д):
1. 0,5% А 0,5
2. 5% Б 5
3. 50% В 0,005
4. 500% Г 50
Д 0,05
2.2. Установити відповідність між кількістю точок, які не лежать в одній площині (1–4) та найбільшою з них кількістю точок (А–Д), які можуть лежати на одній прямій:
1. 6 А 6
2. 8 Б 4
3. 12 В 16
4. 20 Г 10
Д 18
3.1. Яка область визначення функції ![]() .
.
3.2. У кулі на відстані 12 см від її центра проведено переріз, площа якого дорівнює 64 см2. Знайти площу поверхні кулі.
Варіант 3
1.1. Знайти значення виразу 94m ∙ 9–2m при m=![]() .
.
А) 1 ; Б) 81 ; В) 3 ; Г) 9.
1.2. Знайти область визначення функції ![]() ?
?
А) (7;∞); Б) (∞;7)ᴗ(7; ∞); В) [7;∞); Г) (∞;∞).
1.3. Знайти множину значень функції у=sin x –2.
А) [–1;1] ; Б) [–2;0]; В) [–3;0]; Г) [–3;–1].
1.4. Обчислити значення виразу cos 390cos 210 – sin 390 sin 210.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г) 1.
; Г) 1.
1.5. Скоротити дріб 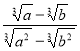 .
.
А) ![]() ; В)
; В) ![]() ;
;
Б) ![]() ; Г)
; Г) ![]() .
.
1.6. Розв’язати нерівність 0,2 х–2 0,008.
А) [5;∞); Б) (–∞;5]; В) (–∞;4]; Г) [4;∞).
1.7. Яка з поданих функцій є первісною функції f(x)=3x ?
А) ![]() ; Б)
; Б) ![]() ; В)
; В)![]() ; Г)
; Г) ![]() .
.
1.8. Гральний кубик підкинули один раз. Яка ймовірність того, що випало число, кратне 3?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г) 1.
; Г) 1.
1.9. Знайти модуль вектора ![]() (–5;1;2).
(–5;1;2).
А) 8 ; Б) 30; В) ![]() ; Г)
; Г) ![]() .
.
1.10. Радіус однієї кулі у 2 рази більший за радіус другої кулі. Чому дорівнює об’єм кулі більшого радіуса, якщо об’єм кулі меншого радіуса дорівнює 1 см3?
А) 8 см3 ; Б) 4 см3; В) 6 см3; Г) 2 см3.
2.1. Установити відповідність між тригонометричними функціями кута β (1–4) та їх значеннями (А–Д), який відповідає точці ![]() одиничного кола:
одиничного кола:
1. sin β А ![]()
2. cos β Б ![]()
3. tg β В ![]()
4. ctg β Г ![]()
Д ![]()
2.2. Установити відповідність між вимірами прямокутного паралелепіпеда (1–4) та довжиною його діагоналі (А–Д):
1. 3 см, 4 см, 5 см А ![]()
2. 3 см, 6 см, 5 см Б ![]()
3. 2 см, 4 см, 7 см В ![]()
4. 3 см, 7 см, 3 см Г ![]()
Д ![]()
3.1. Знайти похідну функції ![]() .
.
3.2. Площа поверхні конуса дорівнює 200 см2, а його твірна дорівнює 17 см. Знайти об’єм конуса.
Варіант 4
1.1. Між якими двома послідовними натуральними числами міститься число![]() .
.
А) 1 і 2; Б) 2 і 3; В) 3 і 4; Г) 4 і 5.
1.2. Відомо, що 0,7m > 0,7n. Порівняйте m і n.
А) m < n ; Б) m > n; В) m = n; Г) m n.
1.3. Яка геометрична фігура не може слугувати графіком деякої функції?
А) пряма ; Б) коло; В) парабола; Г) точка.
1.4. Відомо, що log3 5=а. Чому дорівнює значення виразу log9 25?
А) а2; Б) 2а; В) ![]() ; Г) а.
; Г) а.
1.5. Розв’язати рівняння соs 3x = ![]() .
.
А) ![]() ; В)
; В) ![]() ;
;
Б) ![]() ; Г)
; Г) ![]() .
.
1.6. Знайти кутовий коефіцієнт дотичної до графіка функції ![]() у точці з абсцисою х0=0.
у точці з абсцисою х0=0.
А) 0; Б) 1; В) е; Г) 7.
1.7. Знайти загальний вигляд первісної функції f(x) = 3x2 .
А) 3x3 + C; Б) x3 + C; В) x2 + C; Г) 6x + C.
1.8. У лотереї розігрувалося 16 грошових призів і 20 речових. Усього було випущено 100 лотерейних білетів. Яка ймовірність, придбавши один білет, не виграти жодного призу?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.9. Точка С – середина відрізка АВ, А(2;4;6), С(0;1;10). Знайти координати точки В.
А) В(1;2,5;8); Б) В (–2;–2;14); В) В (–2;–3;4); Г) В (2;6;26).
1.10. Обчислити об’єм правильної трикутної призми, сторона основи якої дорівнює 20 см, а висота дорівнює 9см.
А) 300![]() см3 ; Б) 300 см3; В) 900 см3; Г) 900
см3 ; Б) 300 см3; В) 900 см3; Г) 900![]() см3.
см3.
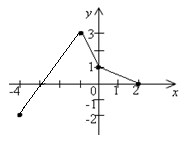 2.1. Установити відповідність між властивостями функції f(x) (1–4), зображеної на рисунку графіком на відрізку [–4;2], та проміжками (А–Д):
2.1. Установити відповідність між властивостями функції f(x) (1–4), зображеної на рисунку графіком на відрізку [–4;2], та проміжками (А–Д):
1. функція f(x) зростає на проміжку А [–4;–3]
2. функція f(x) спадає на проміжку Б [–3;2]
3. функція f(x)≤0 на проміжку В [–4;–1]
4. функція f(x)≥0 на проміжку Г [–2;3]
Д [–1;2]
2.2. Установити відповідність між векторами (1–4) та їх скалярними добутками (А–Д):
1. ![]() (1;5;14) і
(1;5;14) і ![]() (3;4;–1) А 7
(3;4;–1) А 7
2. ![]() (3;0;–4) і
(3;0;–4) і ![]() (5;–7;2) Б 9
(5;–7;2) Б 9
3. ![]() (4;–2;9) і
(4;–2;9) і ![]() (–3;1;4) В –6
(–3;1;4) В –6
4. ![]() (5;–4;–1) і
(5;–4;–1) і ![]() (3;4;5) Г 22
(3;4;5) Г 22
Д 5
3.1. Розв’язати рівняння ![]() .
.
3.2. Об’єм конуса з радіусом основи 6 см дорівнює 96 см3. Обчислити площу бічної поверхні конуса..
Варіант 5
1.1. Спростити вираз ![]() .
.
А) 13; Б) 138![]() ; В) 11; Г) 118
; В) 11; Г) 118![]() .
.
1.2. Яка з наведених функцій є показниковою?
А) ![]() ; Б) у = х4 ; В) у = 4х ; Г)
; Б) у = х4 ; В) у = 4х ; Г)![]() .
.
1.3. Графік якої з наведених функцій проходить через точку А(2;1)?
А) у=lg(x1); Б) y=cos x; В) ![]() ; Г) y=|x+1|.
; Г) y=|x+1|.
1.4. Обчислити значення виразу 2 sin22,50 cos22,50.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.5. Розв’язати рівняння tg 2х = 4.
А)![]() ; Б)
; Б)![]() ; В)
; В)![]() ; Г)
; Г) ![]() .
.
1.6. Знайти похідну функції ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.7. Обчислити інтеграл: ![]() .
.
А) –![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.8. З 4 студентів потрібно вибрати двох для поїздки за кордон. Скільки варіантів вибору цих двох студентів існує?
А) 6 ; Б) 12; В) 15; Г) 18.
1.9. Яка з точок А(7;9;0); В(0;–8;6); С(–4;0;5) належить координатній площині xz?
А) точка А ; В) точка С ;
Б) точка В ; Г) жодна з даних точок.
1.10. Обчислити об’єм правильної трикутної піраміди, сторона основи якої дорівнює 6 см, а висота дорівнює 9см.
А) 12![]() см3; Б) 9
см3; Б) 9![]() см3; В) 27
см3; В) 27![]() см3; Г) 81
см3; Г) 81![]() см3.
см3.
2.1. Установити відповідність між функціями (1–4) та їх областями визначення (А–Д):
-
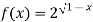 А
А 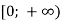
-
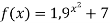 Б
Б 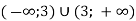
-
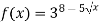 В
В 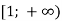
-
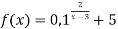 Г
Г 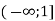
Д ![]()
2.2. Установити відповідність між задачами (1–4) та відповідями до них (А–Д):
1. У куб вписано кулю, радіус якої 3,5. Обчислити об’єм куба. А 96
2. У куб вписано кулю, радіус якої 2. Б 48
Обчислити площу повної поверхні куба. В 24
3. У куб вписано кулю, діаметр якої 6. Обчислити об’єм куба. Г 343
4. У куб вписано кулю, діаметр якої 2. Д 216
Обчислити площу повної поверхні куба.
3.1. Знайти sin α, якщо cos α = –![]() і <α<
і <α<![]() .
.
3.2. Відрізок, що сполучає центр верхньої основи циліндра з точкою кола нижньої основи, дорівнює 6 см. Знайти площу бічної поверхні циліндра, якщо його висота дорівнює діаметру основи.
Варіант 6
1.1. Відомо, що 3х : 3у=81 . Чому дорівнює значення виразу х – у ?
А) 0; Б) 2; В) 3; Г) 4.
1.2. Знайти значення виразу ![]() .
.
А) 3; Б) –3; В) ![]() ; Г) 9.
; Г) 9.
1.3. Яка з даних функцій є зростаючою?
А) у=0,1х; Б) у=10х; В) у=10; Г) у=![]() .
.
1.4. Знайти область визначення функції ![]() .
.
А) (∞;2]ᴗ[3;∞); Б) (∞;2]; В) [3;∞); Г) [2;3].
1.5. Обчислити значення виразу sin 560 cos 340 + cos 560 sin 340.
А) ![]() ; Б)
; Б) ![]() ; В) 1; Г) 0.
; В) 1; Г) 0.
1.6. Знайти похідну функції y=ex – 3x2.
А) ![]() ex – 6x; В)
ex – 6x; В) ![]() ex – x3;
ex – x3;
Б) ![]() xex-1– 6x ; Г)
xex-1– 6x ; Г) ![]() xex-1– x3.
xex-1– x3.
1.7. Обчислити інтеграл: 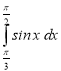 .
.
А) 1,5; Б) 0,5; В) –1,5; Г) –0,5.
1.8. У шухляді лежать чотири картки, на яких написано числа 1, 2, 3 і 5. Яка ймовірність того, що добуток чисел, записаних на двох навмання вийнятих картках, є непарним числом?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.9. Знайти різницю векторів ![]() (2;7;–4) і
(2;7;–4) і ![]() (–1;5;3).
(–1;5;3).
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.10. Обчислити об’єм циліндра, радіус основи якого дорівнює 7 см, а твірна дорівнює 5 см.
А) 35 см3 ; Б) 175 см3; В) 70 см3; Г) 245 см3.
2.1. Установити відповідність між рівняннями (1–4) та їх розв’язками (А–Д):
1. ![]() А Ø
А Ø
2. ![]() Б –1
Б –1
3. ![]() В 3
В 3
4. ![]() Г 8
Г 8
Д 21
2.2. Установити відповідність між парами точок (1–4) та відстанями між цими точками (А–Д):
1. А(1;3;4), В(2;1;2) А 3
2. В(3;5;1), М(0;1;1) Б 13
3. D(–2;3;4), С(6;3;–2) В 5
4. К(1;–2;5), Р(1;10;0) Г 7
Д 10
3.1. Знайти проміжки зростання функції ![]() .
.
3.2. Основа прямої призми ромб з гострим кутом 300. Діагональ бічної грані утворює з площиною основи кут 600. Знайти об’єм призми, якщо її висота дорівнює 6 см.
Варіант 7
1.1. Значення якого з поданих виразів найбільше?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.2. Розв’язати рівняння ![]() .
.
А) 12; Б) 64;64; В)64; Г) коренів немає.
1.3. Розв’язати нерівність 0,4х > 1.
А) (0;∞) ; Б) (–∞;0) ; В) (1;∞) ; Г) (–∞;1).
1.4. Чому дорівнює значення виразу ![]() .
.
А) 4; Б) 5; В) 3; Г) 8.
1.5. Розв’язати рівняння tg х = 0.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.6. Знайти значення похідної функції f(x) = x2 – 5х в точці х0=2.
А) 1; Б) –1; В) –3; Г) 3.
1.7. Обчислити інтеграл 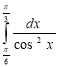 .
.
А) ![]() ; Б) –
; Б) –![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.8. Чому дорівнює ймовірність того, що при киданні грального кубика випаде число, яке більше за 2?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.9. Знайти координати середини відрізка МК, якщо М(20;–18;6), К(–12;–2;4).
А) (8;–20;10); Б) (4;–10;5); В) (–16;–10;5); Г) (8;–10;5).
1.10. Обчислити площу бічної поверхні конуса, радіус основи якого дорівнює 3 см, а твірна у 3 рази більша за радіус.
А) 27 см2 ; Б) 81 см2; В) 12 см2; Г) 30 см2.
2.1 Установити відповідність між функціями (1–4) та проміжками їх зростання (А–Д):
1. ![]() А (–;0]
А (–;0]
2. ![]() Б [0;+)
Б [0;+)
3. ![]() В (–;–3]
В (–;–3]
4. ![]() Г [–3;+)
Г [–3;+)
Д [3;+)
2.2. Сторона куба дорівнює 10 см. Установити відповідність між задачами (1–4) та відповідями до них (А–Д):
1. Знайти площу повної поверхні куба. А 400
2. Знайти об’єм куба. Б 10![]()
3. Обчислити довжину діагоналі куба. В 1000
4. Знайти площу бічної поверхні куба. Г 10![]()
Д 600
3.3. Знайти первісну функції ![]() , графік якої проходить через точку N(9;-8).
, графік якої проходить через точку N(9;-8).
3.4. Точка А знаходиться на відстані 9 см від площини α. Похилі АВ і АС утворюють із площиною α кути 450 і 600 відповідно, а кут між проекціями похилих на площину α дорівнює 1500. Знайти відстань між точками В і С.
Варіант 8
1.1. Спростити вираз ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.2. Знайти значення виразу![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В)![]() ; Г)
; Г) ![]() .
.
1.3. Графіком якої з функцій є гіпербола?
А) у=![]() ; Б) у=
; Б) у=![]() ; В) у=
; В) у=![]() ; Г) у=6х.
; Г) у=6х.
1.4. Областю визначення якої з даних функцій є множина всіх дійсних чисел?
А) у=lg(x+1); Б) у=lg(x21); В) у=lg(x2+1); Г) у=lg x2.
1.5. Розв’язати нерівність ![]() .
.
А) (-∞;3] ; Б) (0;3] ; В) [0;3] ; Г) (-∞;9].
1.6 Знайти похідну функції y=e2x.
А) ![]() 2xe2х-1; Б)
2xe2х-1; Б) ![]()
![]() e2х ; В)
e2х ; В) ![]() e2х; Г)
e2х; Г) ![]() 2e2х.
2e2х.
1.7. Обчислити інтеграл: ![]() .
.
А) 15; Б) 30; В) –15; Г) –30.
1.8. У коробці лежать 18 зелених і 12 блакитних кульок. Яка ймовірність того, що обрана навмання кулька виявиться блакитною?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.9. Знайти координати вектора ![]() , якщо М(10;–4;2) , К(16;2;–5).
, якщо М(10;–4;2) , К(16;2;–5).
А) ![]() (–6;–6;7); В)
(–6;–6;7); В) ![]() (6;6;–7);
(6;6;–7);
Б) ![]() (16;–2;–3); Г)
(16;–2;–3); Г) ![]() (6;–2;–3).
(6;–2;–3).
1.10. Обчислити об’єм піраміди, основою якої є прямокутник зі сторонами 6 см і 10 см, а висота піраміди дорівнює 15 см.
А) 300 см3 ; Б) 900 см3; В) 480 см3; Г) 240 см3.
2.1. Установити відповідність між числами (1–4) та їх середніми арифметичними (А–Д):
1. 34; 67; 23; 68 А 8,5
2. 6,2; 4,6; 32,1 Б 14,3
3. 8,3; 5,2; 4,5; 22; 2,5 В 45,5
4. 4; 98; 34; 46 Г 36,4
Д 48
2.2. Установити відповідність між геометричними тілами (1–4) та формулами для визначення їх об’ємів (А–Д):
1. циліндр А ![]()
2. куля Б ![]()
3. призма В ![]()
4. піраміда Г ![]()
Д ![]()
3.1. Знайти значення х, якщо log 7 х = log 7 2,5 + 4log 7 2 – log 7 10.
3.2. Паралельно осі циліндра проведено переріз, який є квадратом зі стороною 6 см і відтинає від кола основи дугу, градусна міра якої дорівнює 900. Знайти площу бічної поверхні циліндра.


про публікацію авторської розробки
Додати розробку
