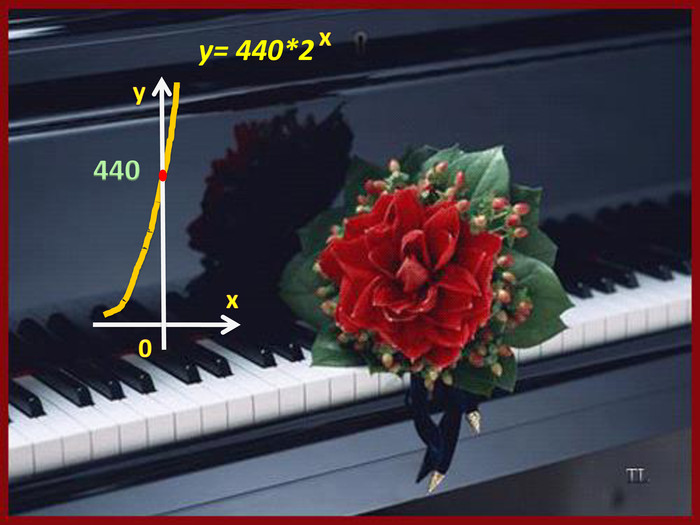
Урок-фрейм"Показникова функція у природі, науці, техніці"

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку: Показникова функція у природі, науці, техніці.

Тип уроку: урок закріплення і удосконалення нових знань, умінь і навичок.

Вид уроку: урок -фрейм.

Навчальна мета:

• навчити учнів застосовувати набуті знання про показникову функцію, зокрема, розглянути приклади застосування показникової функції у економіці, фізиці, біології,  медицині та музиці;
• показати дію закону діалектики – єдності і боротьби протилежностей, об’єднати різноманітні  процеси в природі і техніці.

Розвиваюча:

• розвивати математичну культуру учнів, розширити і поглибити рамки навчальної програми шляхом міжпредметних зв’язків;
• привчити учнів користуватися додатковою літературою, робити висновки і узагальнення.

Виховна:

• виховувати інтерес до математики, наполегливість, самостійність, відповідальність та вимогливість до себе.

Методична мета: Рівнева диференціація на уроках математики.

Міжпредметні зв’язки:

• фізика - тема – „Закони руху в механіці”, „Будова і властивості твердих тіл”, „Реактивний рух”.
• біологія - тема – „Будова клітин прокаріот”.

Забезпечення уроку:  комп’ютер, проектор, таблиці оцінювання доповідачів.

                                           Девіз уроку:

„Недостатньо лише мати добрий розум. Головне – раціонально застосовувати його.”

                             Р. Декарт

Хід уроку

I. Перевірка присутності і готовності учнів до уроку – 1 хв.

II. Актуалізація опорних знань (усне опитування) – 5 хв.

III. Специфіка уроку, його мета – 2 хв.

На сьогоднішньому занятті будуть заслухані повідомлення, підготовлені учнями за матеріалами додаткової літератури.

Показникові  функції зустріча­ються в найрізноманітніших галузях науки – фізиці, хімії, біології, економіці, інформатиці, медицині, лісівництві, картографії, будівництві. Математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточую­чий нас світ, ні забезпечити науково-технічний прогрес.

IV. Застосування набутих знань у практичній діяльності – 33 хв.

1 . Показникові функція в економіці- 8 хв

1. Від складних відсотків до показникової функції (показникова функція в банку) – інформація учня - 3 хв.
2. Задача про приріст населення – 2хв
3. Показникова функція та інформаційний бум  (повідомлення учня) - 2 хв
4. Реклама буклету -1хв

2. Тесова перевірка знань – 5 хв.
3.          Показникова функція в фізиці – 10 хв.

Виступ учнів по питаннях:

1. Чи може одна людина втримати корабель?- 3хв.
2. Задачі про радіоактивний розпад-3хв
3. Визначення температури чайника, який охолоджується в певний момент часу -3 хв.
4. Реклама збірки -1хв

4. Показникова функція в біології та медицині (повідомлення учня)  – 4 хв.

Реклама газети- 1хв.

5. Розування показникових рівнянь (робота в парі). Інтерактивна вправа «Склади алгоритм» - 7хв
6. Показникові функція в музиці - 3хв

V. Підведення підсумків – 4 хв.

1. Висновки:

• аналіз діяльності учнів у процесі всього уроку;
• повідомлення та обґрунтування оцінок.

2. Домашнє завдання:

1. Знайти значення функції 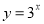, якщо x = 2, x  =  -2, x = 0.
2. Знайти область визначення функції .
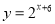3. Побудувати графік функції .

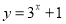І Організаційний етап

 

Те, про що ми будемо говорити на сьогоднішньому уроці, уже відкрито. Але, можливо, щось нове ви відкриєте сьогодні для себе. На попередніх уроках ми ознайомились з показниковою функцією, її графіком та властивостями, розв’язували вправи зі степенями, вчились розв’язувати показникові рівняння. І весь цей час у вас, мабуть, виникало питання : «А навіщо?».

І наш урок повинен стати відповіддю на це запитання.

Урок- фрейм “ Показникова функція у природі, науці, техніці ” - це урок, центром якого є поняття показникової функції, яке сприймає психіка в обмежених рамках простору і часу. Фрейм охоплює все інформаційне оточення даного поняття, правила, формули...

Фрейм (з англійського -  рамка) означає консолідацію різнорідної інформації, що має центром те або інше реальне явище, дію, подію, ситуацію, сприйняту психікою в обмежених рамках простору і часу.

                                           Девіз уроку:

„Недостатньо лише мати добрий розум. Головне – раціонально застосовувати його.”

                             Р. Декарт

ІІ Актуалізація опорних знань

Бліц-опитування (презентація «Урок-фрейм»)

1.              Що означає «експоненціальна функція» (показникова функція).
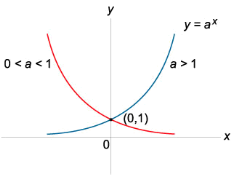
2.              Яка функція називається показниковою ( функція виду у=а^х , де а>0 і а≠1)
3.              Скільки розв’язків має показникове рівняння 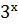=1 (один).
4.              Як розміщено графік показникової функції в системі координат, якщо її основа – відємне число? (не існує такої функції).
5.              В якій точці графік функції y= 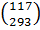^x перетне вісь у?    (0;1)
6.              Назвіть число, яке ставши показником степеня, враз зрівнює всі числа. (нуль).
7.              Чи мають спільну точку графіки функцій 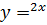та y=(5/2) ^x, якщо так, то назвіть її координати.
8.              За якої умови 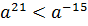      (якщо а<1).
9.              Чому дорівнює значення виразу а^х, якщо x=tg15*ctg15           (a)
10.          Яку властивість показникової функції обов’язково використовують під час розв’язування показникових нерівностей.       (монотонність)
11.  Назвіть функцію, графік якої симетричний графіку функції   y=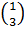^x

 відносно осі ординат.           (y=3^x)

12. Область визначення функції (х є R )
13. Область значення (у>0)

ІІІ.  Мотивація навчальної діяльності.

 Більшість процесів у житті пов’язано із залежністю між величинами. Наприклад, кількість виконаної роботи залежить від її обсягу та складності самої роботи, рівень знань учня від рівня його інтелектуального розвитку вартість покупки від кількості купленого товару і цін. Одна залежність носить випадковий характер, інші постійні.  Розглянемо різноманітні процеси, які проходять в природі.

Готуючись до уроку, ви отримали проблемні питання, щоб відповісти на

 запитання  : «А навіщо?».

Тема уроку : Показникова функція у природі, науці, техніці.

Показникові  функції зустріча­ються в найрізноманітніших галузях науки – фізиці, хімії, біології, економіці, інформатиці, медицині, лісівництві, картографії, будівництві.

 

 IV. Застосування набутих знань у практичній діяльності

А почнемо ми з економістів а точніше з банків, а ще точніше з їх попе­редників — лихварів.

 

1.     І група Показникова функція в економіці

(презентація «Еконміка+показникова функція»)

„Показникова функція в банку”.

Ще за стародавніх часів було широ­ко поширене лихварство — віддавання грошей у позику під відсотки. Селянин у разі неврожаю, ремісник, майно якого знищила пожежа, розо­рений торгівець змушені були йти до лихваря, обіцяючи наступного року повернути суму знач­но більшу, ніж узята в позику. Наприклад, у Дав­ньому Вавилоні лихварі брали по 20 % лихви на рік. При цьому, якщо боржник не міг повернути борг наступного року, йому треба було платити відсотки не тільки з позиченого капіталу, а й з відсотків, що виросли за рік. Тому через 2 роки слід було заплатити не 40 %, а 44 % лихви, адже 1,2² = 1,44. За 5 років сума боргу збільшувалася в 1,2⁵ разів, тобто майже в 2,5 рази, а за 10 – років більш ніж у 6 разів. Зрозуміло, що більшість борж­ників були не в змозі повернути борг і, давно вип­лативши основну суму боргу, були змушені все життя працювати на те, щоб виплатити все зро­стаючі відсотки. Нарешті зубожілі боржники ста­вали рабами хижого лихваря.

У XIV—XV ст. у Західній Європі почали з'явля­тися банки (від фр. banque — лава, контора) — ус­танови, які давали гроші в позику князям та куп­цям, фінансували за великі відсотки далекі манд­рівки та завойовницькі походи. Щоб полегшити розрахунки складних відсотків, склали таблиці, за якими відразу можна було дізнатися, яку суму тре­ба виплатити через t років, якщо була взята сума А₀ під p% річних. Легко підрахувати, що сума, яку треба заплатити, виражається формулою:

А=А₀(1+)^t,

 

Якщо р — стале, то А  є функцією від t. Такі таблиці давали значення показникової функції при різних значеннях основи і натураль­них значеннях п.

Останнє обмеження було не дуже зручним: іноді гроші бралися в борг не на ціле число років, а, наприклад, на 2 чи 6 місяців. Так виникла ідея степеня з дробовим показником. Ця ідея нале­жала ще Архімеду, але вона не була зрозумілою його сучасникам. І лише через 1,5 тисячоліття почали розглядати піднесення чисел до степеня з дробовим показником.

Степінь з ірраціональним показником розгля­нув Ісаак Ньютон в XVII ст. Після цього Йоганн Бернуллі розглянув степінь зі змінним дійсним показником, тобто ввів показникову функцію.

Задача про приріст населення.

Хочу запропонувати вам слідуючу задачу. Визначити кількість населення світу у 2014 році, якщо у 2002 році на землі проживало 6 млрд. осіб. Середньорічний приріст населення становить 2%.

Розв'язання

Для обчислення можна скористатися формулою складних відсотків:

А=А₀(1+)^t,

де А-шукана величина,

А₀-відома кількість населення,

р-середньорічний приріст населення у відсотках,

t-розрахунковий термін (t=2014-2002=12 років)

Дістанемо:

А=6*(1+0,02)¹²=6*1,02¹²≈7,6(млрд. осіб)

Відповідь: 7,6 мільярдів осіб.

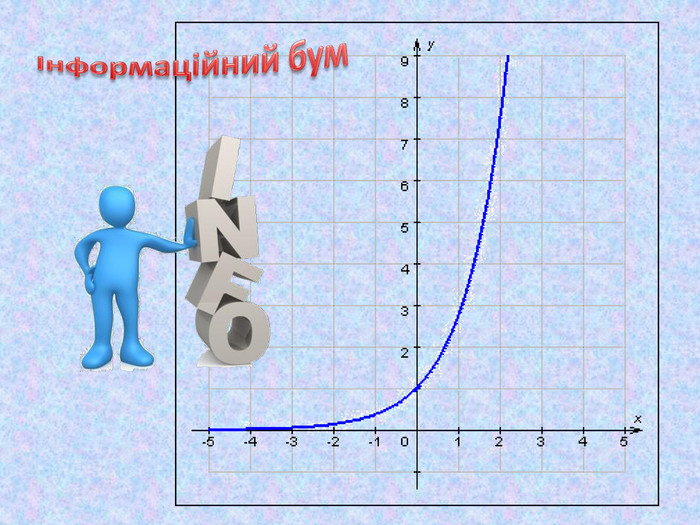
 „Показникова функція та інформаційний бум”.

Нині багато говорять про інформа­ційний бум. Стверджують, що кількість інформації подвоюється кожні десять років. Зобразимо цей процес у вигляді графіка деякої функції.

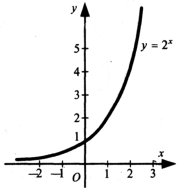
Візьмемо обсяг інформації в де­який початковий рік за 1. Удвічі більший відрізок поставимо над оди­ничною оцінкою, вважаючи, що оцін­ка відповідає першому десятку років. Удвічі більший відрізок відповідає другому десятку років, ще вдвічі більший — третьому і т.д. Обрані нами значення аргументу є елемен­тами арифметичної прогресії: 1, 2, З, ... . У той самий час значення функції зростають за законом геомет­ричної професії: 2, 4, 8, ... . Подиви­мося, який був обсяг інформації до року, прийнятого за початковий. По осі абсцис уліво від початку коорди­нат відкладатимемо значення функції в порядку зменшення — у 2 рази мен­ше з кожним кроком. Сполучимо всі побудовані точки плавною лінією. Перед нами графік показникової функції. Головна особливість графі­ка цієї функції — її крутизна. Показ­никова функція зустрічається в описі процесів, у яких швидкість зміни ве­личини пропорційна до самої величи­ни. (папка «Економісти»)

 

2. Тесова перевірка знань

Тож перевіримо як засвоїли ви попередній потік інформації, чи зростаючою є функція вашої розумової діяльності ( самоперевірка, презентація «Урок - фрейм»)

Завдання: (робота по варіантах)

      І – варіант

          1. Обчислити:

А	Б	В	Г
1	2	4	0

           2. Обчислити :

А	Б	В	Г
1	3	7	5

           3. Спростити вираз: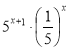                       

А	Б	В	Г
1	5	4	8

 

           4. Визначити х, якщо

А	Б	В	Г
-1	-7	-9	-2

 

  Відповідь:    1757

 

 

      ІІ – варіант

           1. Обчислити:

А	Б	В	Г
1	2	4	0

           2. Обчислити :

А	Б	В	Г
1	3	7	5

           3. Спростити вираз: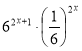                       

А	Б	В	Г
1	6	4	8

           4. Визначити х, якщо

А	Б	В	Г
-1	-7	-9	-6

 

  Відповідь:   1766

 

      ІІІ – варіант

           1. Обчислити: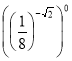

А	Б	В	Г
1	2	4	0

           2. Обчислити :

А	Б	В	Г
1	3	7	5

           3. Спростити вираз: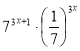                       

А	Б	В	Г
7	6	4	8

 

           4. Визначити х, якщо

А	Б	В	Г
-1	-5	-9	-6

 

  Відповідь:    1775

 

      ІV – варіант

           1. Обчислити: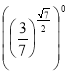

А	Б	В	Г
1	2	4	0

           2. Обчислити :

А	Б	В	Г
1	3	7	5

           3. Спростити вираз: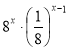                       

А	Б	В	Г
1	6	4	8

           4. Визначити х, якщо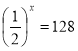

А	Б	В	Г
-1	-7	-9	-6

 

  Відповідь:   1787 

 

      V – варіант

           1. Обчислити:

А	Б	В	Г
1	2	4	0

           2. Обчислити :

А	Б	В	Г
1	3	7	5

           3. Спростити вираз: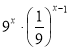                       

А	Б	В	Г
1	9	4	8

 

           4. Визначити х, якщо

А	Б	В	Г
-1	-7	-9	-6

 

  Відповідь: 1791 

 

 

3. Показникова функція в фізиці

 (презентація «Показникова функція + фізика»)

„Чи може людина втримати корабель?” ,як ви гадаєте.

У романі Жуля Верна „Матіас Шандор” виведено образ силача Матіфу, який здійс­нив багато подвигів. Ось один із них.

Готувався спуск на воду корабля. І саме в цей момент до гавані влетіла яхта, яка неминуче врізалася б у корабель, якби з натовпу не вибіг чоловік, який з усієї сили вперся в землю ногами і вчепився в трос, що утримував корабель, щоб затримати спуск. Поблизу стояла гармата. Сміли­вець швидко накинув на неї трос і з нелюдським зусиллям утримував його 10 секунд, поки трос не лопнув. Але цих 10 секунд було досить, щоб яхта проскочила повз корабель — зіткнення не ста­лося. Звичайно, ви здогадалися, що сміливий незнайомець — це Матіфу.

Але чи потрібна нелюдська сила, щоб утрима­ти корабель?

„Чи може людина втримати корабель?”

Згадаємо, як відбувається швартування кораб­ля. З нього кидають канат на берег. Людина, що стоїть на пристані, обмотує кілька разів канат навколо стовпа. Сила тертя між канатом і стов­пом і утримує судно.

Якщо F₀ — прикладена сила, F— сила, що ут­римує корабель, то маємо:

1  виток: F= F₀ • k;

2 витки: F= F₀ •  к²,

3 витки: F= F₀ • k³,

..................................

x квитків: F= F₀ •  k^x;

k залежить від матеріалу, з якого зроблено канат і стовп. Наприклад, коли канат—з конопель, а стовп залізний, то . Тобто, обернувши канат 3 рази, силою 22 Н можна утримувати 40 т.

До речі, це явище ми використовуємо доволі часто, зав'язуючи шнурки на черевиках, вузли­ки на мотузку тощо. Оскільки вузол — це моту­зок, обвитий навколо іншого мотузка, то він тим міцніший, чим більше разів одна частина мотузка сплітається з другою.

         Працюючи над питанням «Застосування показникової функції в фізиці», ми розглянули багато цікавих задач. І щоб наша праця не пропала марно, вирішили випустити збірку «Показникова функція і фізика»

Завдання 1. 26 квітня 2014 виповнюється 28 років аварії на Чорнобильській АС, внаслідок якої територія України була забруднена радіоактивною речовиною. З фізики відомо, що відношення початкової до кінцевої N кількості радіоактивної речовини обчислюється за формулою:

=,

де х-час після аварії,

Т-період напіврозпаду радіоактивної речовини.

Одними з най не безпечніших є атоми радону. Для нього Т≈4 доби.

Задача: Через який час після аварії кількість радіоактивних атомів радону зменшиться у 1024 рази.

Розв'язання:

Задача зводиться до показникового рівняння

; =2¹⁰; =10; х=40

Відповідь 40 діб

 

Завдання  2. Перший міжнародний еталон радію був виготовлений Марією Кюрі в серпні 1911 р. і містив 16,74 мг чистого радію. Яка кількість радію містилася в цьому еталоні в 2013 р., якщо вона обчислюється за формулою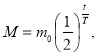

де m _{0 =}16,74 мг, Т = 1600 років і t - час, що минув після 1911. р.?
Рішення. Знайдемо кількість радію в 2013 році:

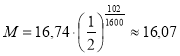мг
Відповідь: 16,07 мг

Завдання 3.   Температура чайника, який  стигне в момент  обчислюється за формулою- . Обчислити через який час температура чайника буде 40˚С.

Рішення :

20·2^0,1τ+80=t·2^0,1τ

t·2^0,1τ - 20·2^0,1τ=80

2^0,1τ (t – 20)=  80

2^0,1τ = 80/(40 - 20)

2^0,1τ = 4

2^0,1τ=2²

0,1τ=2

Τ=20 (хв.)

                    (папка «Фізики»)

 

Наш світ щосекунди змінюється, розглянемо як змінюються популяції організмів в природі.

4. Показникова функція в біології  

                           ( презентація «Біологія + показникові функція»)                        

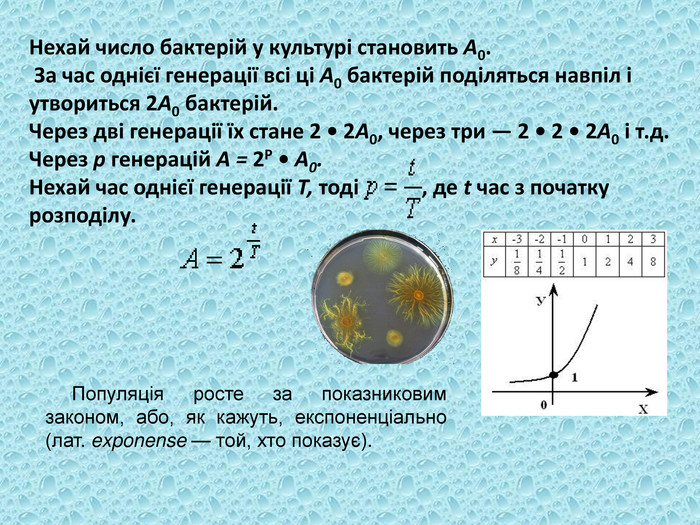
ЗАДАЧА. Нехай число бактерій у культурі становить А₀. За час однієї генерації всі ці А₀ бактерій поділять­ся навпіл і утвориться 2А₀ бактерій. Через дві ге­нерації їх стане 2 • 2А₀, через три — 2 • 2 • 2А₀ і т.д. Через р генерацій А = 2^Р • А₀.

Нехай час однієї генерації Т, тоді , де t час з початку розподілу.   .

Бачимо, що популяція росте за показниковим законом, або, як кажуть, експоненціально (лат. exponense — той, хто показує).

З відкриттям англійським мікробіологом Флемінгом пеніциліну і народженням нової промис­ловості знати кількість грибків, утворених у про­цесі розвитку, стало важливо і можливо при ви­користанні виведеної раніше формули.

ЗАДАЧА. Потомство кімнатних мух за літо тільки від однієї самки може скласти 8 • 10¹⁴. Ці мухи важили б кілька мільйонів тонн, а вибудувані в один ланцюжок, вони склали б відстань, більшу, ніж відстань від Землі до Сонця. Потомство пари мух за 2 роки мало б масу, що перевищує масу земної кулі. І тільки завдяки спільноті тварин і рослин, коли збільшення одного виду тягне за собою зростання кількості його ворогів, встановлюється динамічна рівновага в природі.

Показникова функція в медицині

Коли людина лякається, в кров виділяється адреналін, який потім руйнується, причому швидкість руйнування пропорційна кількості цієї речовини, що ще залишилася в крові.

При діагностиці хвороб нирок часто визнача­ють здатність нирок виводити з крові радіоак­тивні ізотопи, причому їх кількість спадає за по­казниковим законом.

Звичайно, показниковий закон виконується дуже приблизно в біологічних системах, бо ми маємо тут справу з дуже складними системами. (папка «Біологи»)

 

Е. Розв’язування показникових рівнянь (робота в парі).

Інтерактивна вправа «Склади алгоритм»  (презентація «Урок - фрейм»)

Для зниження адреналіну в крові після такого потоку інформації пропоную змінити вид нашої діяльності. Поспілкуйтесь і попрацюйте в парі.

   І пара

             Розв’язати показникові рівняння:

А. Знайти область допустимих значень коренів рівняння	Дорогий друже,
Б. Винести спільний множник за дужки у лівій частині рівняння	Добрий розум,
В. Поділити обидві частини рівняння на 4	робить легким
Г. Перенести невідомі члени рівняння у ліву частину, а відомі – у праву	ти обрав
Д. Записати число 16 у вигляді степеня з основою 2	будь-який
Е. Звести подібні доданки у кожній частині рівняння	хибні дії
Є. Поділити обидві частини рівняння на 64	розв’язання рівняння
Ж.Прирівняти показники степенів обох частин рівняння	спосіб життя

            Відповідь: БВДЖ     Добрий розум, робить легким будь-який спосіб життя.                                             

 

   ІІ пара

             Розв’язати показникові рівняння:

А. Знайти область допустимих значень коренів рівняння	Дорогий друже,
Б. Подати у вигляді добутку двох множників	Більше
В. Винести спільний множник за дужки у лівій частині рівняння	думай
Г. Перенести невідомі члени рівняння у ліву частину, а відомі – у праву	ти обрав
Д. Поділити обидві частини рівняння на 5	і
Е. Звести подібні доданки у кожній частині рівняння	хибні дії
Є. Записати число 64 у вигляді степеня з основою 4	тоді
Ж.Прирівняти показники степенів обох частин рівняння	вирішуй

             Відповідь: БВДЄЖ     Більше думай і тоді вирішуй.

 

 ІІІ пара

           Розв’язати показникові рівняння:

А. Знайти область допустимих значень коренів рівняння	Дорогий друже,
Б. Подати у вигляді добутку двох множників та	Хто думає про науку,
В. Винести спільний множник за дужки у лівій частині рівняння	той любить її, а хто її любить,
Г. Перенести невідомі члени рівняння у ліву частину, а відомі – у праву	ти обрав
Д. Поділити обидві частини рівняння на	той ніколи не перестає вчитися,
Е. Звести подібні доданки у кожній частині рівняння	хибні дії
Є. Записати число 64 у вигляді степеня з основою 4	хоча б зовні він і
Ж.Прирівняти показники степенів обох частин рівняння	здавався бездіяльним

               Відповідь: БВДЄЖ     Хто думає про науку, той любить її, а хто її любить, той ніколи не перестає вчитися, хоча б зовні він і здавався бездіяльним.

  ІV пара

             Розв’язати показникові рівняння:

А. Знайти область допустимих значень коренів рівняння	Дорогий друже,
Б. Подати у вигляді добутку двох множників та	Коли ти твердо
В. Винести спільний множник за дужки у лівій частині рівняння	йдеш шляхом,
Г. Перенести невідомі члени рівняння у ліву частину, а відомі – у праву	ти обрав
Д. Поділити обидві частини рівняння на	яким почав іти, то,
Е. Звести подібні доданки у кожній частині рівняння	хибні дії
Є. Записати число 27 у вигляді степеня з основою 3	на мою думку,
Ж.Прирівняти показники степенів обох частин рівняння	ти щасливий

               Відповідь: БВДЄЖ     Коли ти твердо йдеш шляхом, яким почав іти, то, на           мою думку, ти щасливий.

 

І щоб ви стали ще щасливіші  пропонуємо вам і таку інформацію

6. Показникові функція в музиці 

(презентація «Показникова функція + музика»)

Задача 1.

Висота звука визначається його частотою. Вухо людини здатне сприймати звуки з частотою від 16 до 20 000гц. Відомо, що частота ноти «ля» першої октави – 440гц.Ця частота перевіряється по камертону, і по ній йде настройка піаніно.

Знайти частоти інших нот октави, якщо послідуюча від попередньої відрізняються в  .

Розв’язування. Частоти інших нот пов’язані співвідношенням .

     .

Частота ноти «до»  .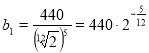

Частота ноти «ре»  .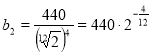

Частота ноти «мі»  .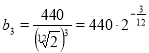

Частота ноти «фа»  .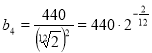

Частота ноти «соль»  .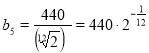

Частота ноти «ля»  .

Частота ноти «сі»  .

Частота ноти «до»  .

b_n= 440*2^n/12    

Послухайте, ви чуєте? Музика . Ми її чуємо  всюди: в поривах вітру, в повітрі, в променях сонця. Вона скрізь. Все, що потрібно, тільки відкритись. Все, що потрібно, тільки слухати.

(папка «Музика + показникова функція»)

V. Підведення підсумків

Вправа «Закінчи речення»

1. Ми сьогодні говорили…
2. Ми сьогодні виконували…
3. Ми сьогодні дізналися…
4. Найбільше зацікавило…

 

Домашнє завдання :

 Повторити властивості показникової функції, властивості степеня.

1.  Знайти значення функції 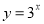, якщо x = 2, x  =  -2, x = 0.
2. Побудувати графік функції .

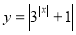 Розглянути способи розв’язування показникових рівнянь

 

РЕФЛЕКСІЯ

Вправа для рефлексії

 Учитель. Розтуліть свою ліву долоню і покладіть на неї той досвід, з яким ви прийшли сьогодні на урок. Відчуйте його значення для вас. А тепер покажіть свою праву долоню і покладіть на неї ту інформацію і той досвід, який ви здобули сьогодні. Відчуйте його цінність для вас.  А тепер з’єднайте долоні, об’єднайте ці досвіди, і нехай вони допоможуть вам успішно здати  зовнішнє незалежне оцінювання. Успіхів вам

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Більшість процесів у житті пов’язано із залежністю між величинами. Наприклад, кількість виконаної роботи залежить від її обсягу та складності самої роботи, рівень знань учня від рівня його інтелектуального розвитку вартість покупки від кількості купленого товару і цін. Одна залежність носить випадковий характер, інші постійні.  Розглянемо різноманітні процеси, які проходять в природі.

У романі Жуля Верна „Матіас Шандор” виведено образ силача Матіфу, який здійс­нив багато подвигів. Ось один із них.

Готувався спуск на воду корабля. І саме в цей момент до гавані влетіла яхта, яка неминуче врізалася б у корабель, якби з натовпу не вибіг чоловік, який з усієї сили вперся в землю ногами і вчепився в трос, що утримував корабель, щоб затримати спуск. Поблизу стояла гармата. Сміли­вець швидко накинув на неї трос і з нелюдським зусиллям утримував його 10 секунд, поки трос не лопнув. Але цих 10 секунд було досить, щоб яхта проскочила повз корабель — зіткнення не ста­лося. Звичайно, ви здогадалися, що сміливий незнайомець — це Матіфу.

Але чи потрібна нелюдська сила, щоб утрима­ти корабель?

„Чи може людина втримати корабель?”

Згадаємо, як відбувається швартування кораб­ля. З нього кидають канат на берег. Людина, що стоїть на пристані, обмотує кілька разів канат навколо стовпа. Сила тертя між канатом і стов­пом і утримує судно.

Якщо F₀ — прикладена сила, F— сила, що ут­римує корабель, то маємо:

1  виток: F= F₀ • k;

2 витки: F= F₀ •  к²,

3 витки: F= F₀ • k³,

..................................

x квитків: F= F₀ •  k^x;

k залежить від матеріалу, з якого зроблено канат і стовп. Наприклад, коли канат—з конопель, а стовп залізний, то . Тобто, обернувши канат 3 рази, силою 22 Н можна утримувати 40 т.

До речі, це явище ми використовуємо доволі часто, зав'язуючи шнурки на черевиках, вузли­ки на мотузку тощо. Оскільки вузол — це моту­зок, обвитий навколо іншого мотузка, то він тим міцніший, чим більше разів одна частина мотузка сплітається з другою.

Зараз  багато морів та океанів  борознять дослідницькі кораблі. У заздалегідь встановлених місцях вони зупиняються і опускають за борт  трос, на кінці якого знаходяться прилади.  Їх опускають на дно, а потім піднімають вгору і записують показники. Але іноді  відбувається неприємна подія -  трос розривається і всі цінні прилади опиняються назавжди на дні моря.

Здавалось, що цієї проблеми можна було б уникнути, якщо зробити трос товщим. Але тут виникає нове ускладнення – верхні частини троса повинні утримувати не тільки прилади, які занурюють, але й нижню частину троса, тому при потовщенні  троса на верхню частину ляже дуже велике навантаження.

Тому доцільно робити нижню частину тросу тоншою, ніж верхню. Виникає питання:  як повинна змінюватись товщина тросу для того, щоб в будь якому перерізі його на 1 см² приходилась одне й те ж саме навантаження?

Досліди цього питання показали, що площа перерізу тросу повинна змінюватись  за законом: , де

S₀ – площа нижнього перерізу,

S – площа перерізу на висоті   х від нижнього перерізу,

γ – питома вага матеріалу, із якого зроблено трос,

Р – вага в воді вантажу, який  опускають.

Такий трос називають тросом рівного опору розриву. Він має найменшу масу, ніж трос постійного перерізу, який розрахований на таке ж навантаження.

 Здавалося б, що спільного між вми­канням і вимиканням струму і падінням з пара­шутом. Але виявляється, що ці процеси відбува­ються за одним законом.

„Падіння з парашутом”.

При падінні тіл у безповітряному просторі їх швидкість рівномірно збільшується. Інакше відбувається падіння в повітрі. Вважає­мо, що сила опору повітря пропорційна швидкості падіння, тобто (знак „мінус” пока­зує, що напрям сили опору повітря направлений вбік, протилежний напряму падіння). Через t секунд після початку падіння швидкість

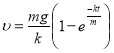, де m – маса парашутиста.

Коли t збільшується, то зменшується і прямує до 0, вираз у дужках прямує до 1, , тобто падіння стане рівномірним;

k залежить від густини повітря, площі поверхні тіла, що падає, тощо.

При падінні тіл у безповітряному просторі швидкість їх безперервно зростає. При падінні тіл в повітрі швидкість падіння теж збільшується, але не може перевершити певної величини

Наприклад, при падінні з парашутом цей кое­фіцієнт доволі великий, і тому швидкість призем­лення парашутиста порівняно мала — 5 м/с. Ясно, що швидкість падіння пушинки буде меншою, ніж швидкість падіння свинцевої кульки, що має ту саму масу, бо пушинка має більшу площу поверхні і тому більше значення k;. Саме тому пушинка так повільно опускається вниз і так легко підхоп­люється потоком повітря. Аристотель у своїх міркуваннях не враховував опору повітря і вважав, що важкі тіла у стільки разів падають швидше за легкі, у скільки разів вони важчі за них. Галілей експериментально заперечив це твердження, ки­даючи кулі з похилої Пізанської башти.

Останнім часом у засобах масової інформації з'явилося багато повідомлень про цю башту і про проекти запобігання її падіння. Ду­маю, що всім буде цікаво дізнатися дещо про неї.

Пізанська башта — не окрема спо­руда, це дзвіниця собору Санта-Марія Маджоре в місті Піза — шедевра світової архітектури, ство­рення його почалося ще в 1063 році. Але не­скінченний потік туристів приваблює саме ця «падаюча вежа», її будівництво розпочали в 1174 році майстри з Інсбрука Вільгельм і Баннано. Побудувавши перший поверх висотою 11 метрів і 2 колонадних кільця, Баннано виявив, що дзвіниця відхилилася на 4 см від вертикалі. Май­стри припинили роботу і зникли з міста. Лише через 100 років знайшовся сміливець, який на­важився продовжити будівництво. Це був архі­тектор Джованні ді Симоні. Але й він, досягши п'ятого поверху, припинив роботу, бо на той час відхилення від вертикалі становило вже 22 см. Ще через 75 років узявся за роботу архітектор Томазо ді Андре. Він завершив будівництво, підняв­ши шостий поверх з похилого боку на 11 см і по­ставивши на восьмому поверсі бронзовий дзвін. І хоч висота башти планувалася 98 м, а остаточна висота була лише 56 м, подолавши 294 сходин­ки, туристи можуть оглядати всю навколишню місцевість і уявляти, що на цьому місці стояв сам Галілео Галілей і виконував свої досліди, про які ми зараз ведемо з вами мову.

Дослідники вважають, що причиною нахилу башти було використання першими майстрами насосів для відкачування води, які були встанов­лені в центрі круглої башти, і вода стікала в один бік — у напрямі річки Арно. Останнім часом ар­хітекторів турбує, що кут нахилу Пізанської баш­ти збільшився, тому існує ризик, що вона — не дай Боже! — може завалитися. У 1994 році вста­новили для підтримки спеціальні свинцеві про­тиваги, в 2001 році провели цілий комплекс профілактичних робіт з укріплення фундаменту, аби зберегти вежу від падіння. Декілька цікавих деталей: у середині 80-х років XX століття відхи­лення від вертикалі досягло 4,22 м, за останні десятиліття воно збільшується в середньому на 1,2 мм за рік. У 1982 році цей процес практично зупинився, але дзвіниця сама трохи повернулася навколо своєї осі на південний захід. Тому зараз непоодинокі виступи спеціалістів за те, щоб „башту залишити в спокої”, бо будь-яке втручан­ня несе для неї загрозу. „Нехай вона сама себе стабілізує”, — кажуть вони. Пізанська башта ва­жить понад 14 т, і якщо її нахил не буде переви­щувати 1 мм на рік, то вона впаде не раніше, ніж через два тисячоліття. 

3акон Ціолковського.

Багато складних задач доводиться розв'язувати в теорії міжпланетних подорожей. Однією з них є задача про визначення кількості палива, необхідного для того, щоб надати ракеті швидкість υ₁, потрібну для досягнення Місяця, Венери, Марса або якоїсь іншої планети. Ця кількість залежить від маси m₀ самої ракети (без палива) і від швидкості υ_о, з якою продукти зго­ряння витікають із сопла ракетного двигуна.

К. Е. Ціолковський розглянув задачу про па­ливо, нехтуючи опором повітря і притяганням Землі.

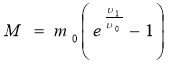
Для ракети масою 1,5 т потрібно за цією фор­мулою 40т пального. Вихід знайшов С. Корольов, запропонувавши багатоступінчасті ракети.

До речі, вам цікаво буде знати, що всі названі четверо генеральних конструкторів ракетно-кос­мічної техніки (С. Корольов, М. Янгель, В. Че-лемей і В. Глушко) — українці, а К. Ціолковсь­кий — прямий нащадок Северина Наливайка; його батько, Едуард Ціолковськлй, що мав по­двійне прізвище Ціолковський-Наливайко, на­родився на Рівненщині, у селі Коростятин, мав родичів у Львові.

 

Розташування планет

Досліджуючи розташування планет сонячної системи навколо Сонця, німецький астроном І.Є. Боде в 1772 склав наступну таблицю:

№	Планета	Відстань (L) до Сонця (в астрономічних одиницях)
1	Меркурій	0,4
2	Венера	0,7
3	Земля	1
4	Марс	1,5
5
6	Юпітер	5,2
7	Сатурн	9,5

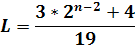До того часу було відкрито тільки шість планет,
тому всі обчислення зупиняються на Сатурні.

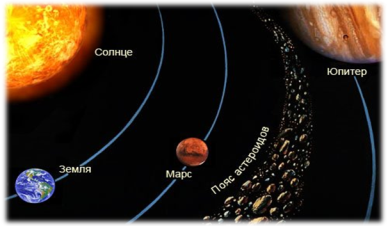Ці обчислення справив І.Є. Боде по наступній формулі:

Дана формула особливо точна для Венери, Землі і Юпітера.
 

Як відомо, між Марсом і Юпітером планети не існує, але якщо
слідувати таблиці Боде, на даній орбіті повинно знаходитися будь-яке космічне тіло. І дійсно, після деяких досліджень вченими
був відкритий пояс астероїдів.
Це було воістину торжеством науки і тріумфом математики!

 

 

Радіоактивний розпад.

Радіоактивний розпад речовини задається формулою  m=m₀(),, де m і m₀ маса радіоактивної речовини у момент часу t і в початковий момент часу t=0; T - період напіврозпаду(проміжок часу, за який первинна кількість речовини зменшується удвічі). Коли радіоактивна речовина розпадається, його кількість зменшується. Через деякий час залишається половина первинної кількості речовини. Чим більше періоду напіврозпаду, тим повільніше розпадається речовина.

Задача .

Період напіврозпаду плутонію Т=140 добам. Який стане маса m плутонію через 10 років, якщо його початкова маса m₀=8г?

  В даній задачі t=10365

 (враховуємо, що в році 365 днів), =.  За формулою радіоактивного розпаду, за допомогою калькулятора  знаходимо

 m=8()1,1345 ^. 10^-7 .

Відповідь. Через 10 років  плутонія залишиться  13 ^. 10^-7 г.

Задача. При радіоактивному розпаді кількість деякої речовини зменшується вдвічі за добу. Скільки речовини залишиться від 250 г через :  а) 1,5 діб; б) 3,5 діб?

Явище радіоактивного розпаду використовується для визначення віку археологічних знахідок, наприклад, визначений зразковий вік Землі                           (близько 5,5 млрд. років).

26 квітня виповнюється 28 років аварії на Чорнобильській АС, внаслідок якої територія України була забруднена радіоактивною речовиною. З фізики відомо, що відношення початкової до кінцевої N кількості радіоактивної речовини обчислюється за формулою:

=,

де х-час після аварії,

Т-період напіврозпаду радіоактивної речовини.

Одними з най не безпечніших є атоми радону. Для нього Т≈4 доби.

Задача: Через який час після аварії кількість радіоактивних атомів радону зменшиться у 1024 рази.

Розв'язання:

Задача зводиться до показникового рівняння

; =2¹⁰; =10; х=40

Відповідь 40 діб

Задача.  Перший міжнародний еталон радію був виготовлений Марією Кюрі в серпні 1911 р. і містив 16,74 мг чистого радію. Яка кількість радію містилася в цьому еталоні в 2013 р., якщо вона обчислюється за формулою 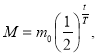де 16,74 мг, Т = 1600 років і t - час, що минув після 1911. р.?
Рішення. Знайдемо кількість радію в 2013 році:

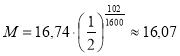мг
Відповідь: 16,07 мг

Задача. Реакція при температурі 50°С протікає за 2 хв. 15 сек. За скільки часу закінчиться ця реакція при температурі 70°С, якщо в даному температурному інтервалі температурний коефіцієнт швидкості реакції дорівнює 3?

Розвязання:

При збільшенні t з 50° до 70° С швидкість реакції у відповідності з правилом Ван-Гоффа зростає :

= γ^(t2-t1)/10

де t₂ = 70° С, t₁=50°C, а υ_t2 и  υ_t1– швидкості реакції за даних температурах.   Звідси

  = 3^(70-50)/10 = 3² = 9

Тобто швидкість реакції збільшиться в 9 раз.

Згідно з визначенням реакції обернено пропорційна t реакції, отже

  ,

де τ час реакції при температурі t₁ і t₂, отже                   

τ _t2 = τ _{t1 *} υ_t1/ υ_t2

враховуючи , що τ _t1= 135 сек., визначаємо t при 70°С:

          τ _t2= 135 * 1/9 = 15 сек.

Відповідь : τ _t2=15 сек.

Наприклад:   Для урану-238 Т = 4,56 млрд. років;                                         для радію-226 Т = 1590 р.;            для цезія-137 Т = 31 р.;                                         для йода-131 Т = 8 суток;                      для радону-222 Т = 3,81 суток.

Зміна температури. Температура Т 100 г піску, нагрітого до 100ºС, зміняються при 0ºС в залежності  від часу  t за формулою:  Т =  100 • 0,8 ^{t .}

Зміна рівня рідини.

Під час витікання рідини  з циліндричної посудини через тонку трубку, розміщену в основі циліндра, висота h рівня  рідини  із зміною часу t  змінюється  по формулі: h=h₀ а^t, де h₀  ─  початковий рівень рідини ; a ─ постійна, яка залежить від діаметра трубки.

 

 

Зміна атмосферного тиску.

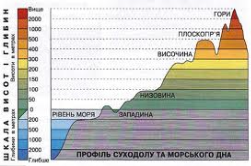Атмосферний тиск змінюється  в залежності  від  висоти h над рівнем моря за законом p = p₀ a^h ,де p ₀ ─ атмосферний  тиск  над  рівнем  моря;   a  ─   постійна величина.

Задача. Залежність тиску атмосфери р (в сантиметрах ртутного стовпа) від вираженої в кілометрах висоти h над рівнем моря виражається формулою. Обчислимо, яким буде атмосферний тиск на вершині Ельбрусу, висота якого 5,6 км?
Розв’язання: Обчислимо атмосферний тиск на вершині Ельбрусу висотою 5,6 км: мм рт. ст.

Коливання маятника

Якщо при коливаннях маятника, гирі, що гойдається на пружині, не нехтувати опором повітря, то амплітуда коливань стає все менше, коливання затухають. Відхилення точки, що здійснює загасаючі коливання, виражається формулою: s=Ae^{-ktsin(хt+х)}. Так як множник е^-kt зменшується з часом, то розмах коливань стає все менше і менше.

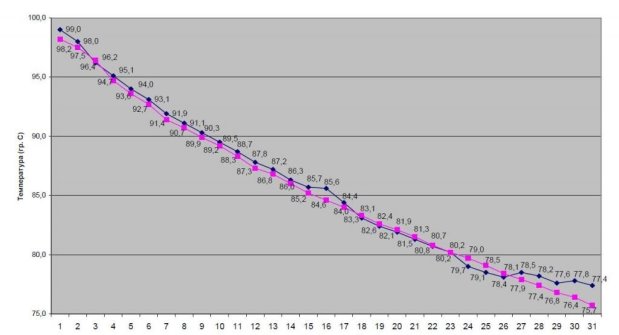
Киплячий чайник.

Усі, напевно, помічали, що якщо зняти киплячий чайник з вогню, то спочатку він швидко остигає, а потім охолодження йде набагато повільніше. Річ у тому, що швидкість охолодження пропорційна різниці між температурою чайника і температурою довкілля. Чим менше стає ця різниця, тим повільніше остигає чайник. Якщо спочатку температура чайника дорівнювала Т₀, а температура повітря Т₁, то через t сeкунд температура Т чайника виразиться формулою:

Т =  (Т₁-Т₀) е^{- кt} + Т₁,

 де до - число, залежне від форми чайника, матеріалу, з якого він зроблений, і кількості води, яка в ньому знаходиться.

Задача. Температура чайника, який  стигне в момент  обчислюється за формулою- . Обчислити через який час температура чайника буде 40˚С.

Рішення :

20·2^0,1τ+80=t·2^0,1τ

t·2^0,1τ - 20·2^0,1τ=80

2^0,1τ (t – 20)=  80

2^0,1τ = 80/(40 - 20)

2^0,1τ = 4

2^0,1τ=2²

0,1τ=2

 Відповідь:  Τ=20 (хв.)

Ми  ще раз пере­коналися, що математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточую­чий нас світ, ні забезпечити науково-технічний прогрес. Як казав великий Ейнштейн : „Природа – це реалізація найпростіших математичних ідей”.

Як бачите, в усіх наведених дослідженнях використовувалася показникова функція.

    Ось деякі з Нобелівських лауреатів, що отримали премію за дослідження в області фізики з використанням показникової функції:

П'єр Кюрі – французький фізик,  лауреат Нобелівської премії з фізики в 1903 році за дослідження явища радіації.

Річардсон Оуен - англійський фізик, лауреат Нобелівської премії з фізики в 1928 році за роботи з вивчення  терміонних явищ, і особливо за відкриття закону, що носить його ім'я.

Ігор Тамм — фізик-теоретик, начальник сектора конструкторського бюро № 11 (Арзамас-16), академік Академії наук СРСР, Нобелівська премія з фізики в 1958 році за дослідження теорії випромінювання Черенкова—Вавилова.

Луїс Альварес - американський фізик та винахідник, дослідник ядерної фізики та космічного випромінювання. Лауреат Нобелівської премії з фізики в 1968 році.

Ганнес Альфвен — шведський фізик і астроном, лауреат Нобелівської премії з фізики 1970 року за внесок у розвиток магнітогідродинаміки.

Роберт Вудро Вільсон, Арно Аллан Пензіасом — американські фізики, лауреати Нобелівської премії з фізики 1978 року «за відкриття мікрохвильового реліктового випромінювання».

Різноманітні застосування показникової (чи її ще називають, експоненціальною) функції надихнули англійського поета Елмера Голила на написання "Оди експоненті", уривок з якої свідчить:

"Нею породжено багато що з того, що "гідно згадки",

Як говорили наші англосакські предки.

 Могутність її породжень

Заздалегідь обумовлено її власною красою і силою,

Бо вони суть фізичне втілення

Абстрактної ідеї є.

Англійські моряки люблять і знають її

Під ім'ям " Гунтер".

Дві шкали Гунтера - ось диво винахідливості.

Експонентою породжена логарифмічна лінійка: у інженера і астронома не було інструменту корисніше, ніж вона.

Навіть витончені мистецтва живляться нею.

Хіба музична гамма не є набір неперових логарифмів?

І таким чином щось абстрактне красиве стало предком одного з найбільших людських досягнень" 

 

 

 

 

 

 

 

Доманівський НВК

«Доманівська ЗОШ І-ІІІ ст №1 –

Центр дитячої та юнацької творчості»