М.В.Наумова " Комбінаторіка"

М.В.Наумова

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                              Тема: Короткі історичні відомості.

                                         Загальні правила комбінаторики.

 

 

                     У багатьох галузях людської діяльності доводиться   

                              зустрічатися з задачами, у яких треба відповістити на запитання: «Скількома способами можна представити, можна зробити, можна вибрати й т.д.?». Відповісти на це питання не завжди легко й просто, тому що не відразу цю кількість способів можна швидко підрахувати, не відразу навіть можна собі представити, а як це взагалі буде відбуватися. Такі задачі вивчає й допомагає вирішувати

комбінаторика - розділ математики, у якому для скінченних множин розглядають різні сполуки (комбінації) елементів.

Цікаво, а звідки з'явилася ця наука й чому, і хто її так назвав?

Якщо хочеш одержати відповідь на це питання прочитай :

 

   Історичні відомості

                                           Термін «комбінаторика» увів Г.Лейбніц в  1666 р. ,                                             термін «сполука комбінація» - Б.Паскаль.

                           Комбінаторні задачі розглядалися ще в стародавності. Так уважають, що  індійські математики вивчали  комбінаторику у зв'язку з її застосуванням у поетиці - науці про структуру римованих рядків , строф, поетичних добутків. Їх, зокрема, цікавив підрахунок кількості можливих об'єднань наголошених і ненаголошених складів строфи, що складається з n складів(2 ст.до н.е.). Однак перші теоретичні дослідження цього розділу математики можна віднести до XVII ст., коли цими питаннями зайнялися відомі французькі математики Б.Паскаль ( 1623-1662) і П.Ферма ( 1601-1665). Ряд комбінаторних задач вирішив Л.Ейлер ( 1707-1783).Займалися питаннями комбінаторики так само И.Ньютон, Н.Тартальі, Я.Бернуллі, М.Штіфель і багато інших відомих учених минулого. Дійсно ж строгою математичною наукою комбінаторика стає в наш час, коли виникла необхідність  користуватися  нею  в хімії, біології, обчислювальній техніці, кібернетиці, економіці.

Загальні правила комбінаторики.

Давайте спробуємо відповістити на запитання: «Скількома способами можна витягти 1 кульку із двох ящиків, якщо в першому ящику 5 кульок, а в другому 7?».

 

Зразок міркування:

 « Я можу взяти кульку з першого ящика. Їх там 5, тоді, якщо їх пронумерувати, то я можу взяти 1-у або 2-у або 3-ю або 4-у або 5-у, тобто способів - 5. Я можу взяти кульку із другого ящика. Їх там 7, тоді, якщо їх пронумерувати, то я можу взяти 1-у або 2-у або 3-ю або 4-у або 5-у або 6-у або 7-у, тобто способів - 7. Із двох ящиків виходить 12 способів». Але адже кульок може бути довільне число, та і ящиків може бути не два, а більше. Та й не кульки можуть бути зовсім. Таким чином, можна розглядати загальне правило:

 Інакше кажучи, сполучник «АБО» означає додавання.

Це так зване правило суми.

Тоді наступна задача, саме так, адже тільки що ми розв'язали задачу по комбінаториці.

Задача №2.

На столі лежать 5 ручок і 4 олівці. Скількома способами можна взяти 1 ручку й 1 олівець?

 

Зразок міркування:

 « Пронумеруємо ручки й олівці. Я можу взяти першу ручку з кожним із чотирьох олівців, це становить чотири способи. Так само можна зробити й із другою ручкою, і з третьою, і із четвертою, і з п'ятою. Тобто загальне число способів буде дорівнювати 5^.4 = 20 ». Але  ручок і олівців може бути довільне число. Таким чином, можна розглядати загальне правило:

 Якщо елемент А можна вибрати n способами, а елемент В  m способами, то « А і В» можна вибрати n^. m способами.

 Інакше кажучи, сполучник «І» означає множення.

                        Це -  правило добутку.

                                              Розв'язати задачу.

                                                         №1.

             У ящику 6 червоних і 5 зелених кубиків. Скількома способами

 можна дістати з нього 1 кубик?

                                                                №2.

            У коробці 5 зошитів в «лінію» і 10 зошитів в «клітку». Скількома способами з її можна взяти один зошит в «лінію» і один зошит в «клітку»?

                                                                   №3.

Скільки існує двозначних чисел, що мають дві парні цифри?

 

 Дай відповідь на питання:

 Чи довідалися ми щось нове на уроці? _______________________________________________________________

Що таке «комбінаторика»?

__________________________________________________________________

Хто ввів цей термін?

__________________________________________________________________

Сформулюй як зрозумів правило суми.

____________________________________________________________________________________________________________________________________

Сформулюй як зрозумів правило добутку.

____________________________________________________________________________________________________________________________________

 

                                                          Завдання до дому.

                      Розв'язати задачі, вивчити конспект.

                                                               №1.

Скільки існує двозначних чисел, що мають дві непарні цифри?

№2.

У ящику 10 червоних і 15 зелених кульок. Скількома способами можна дістати з ящика 1 кульку?

№3.

У  мами Сашка є 5 яблук і 7 груш. Скількома способами мати може дати Сашкові в школу яблуко й грушу?

                                     Тема : Перестановки. Поняття факторіалу.

Давайте довідаємося з яким настроєм ви прийшли на урок.

                                    Перед тобою сонечко, намалюй його личенько у

                                   відповідності з твоїм настроєм.

 

 

 

       А тепер продовжимо нашу подорож по країні Знань. Відкриємо ще одну її таємницю. Для цього нам доведеться відповістити на запитання: «Скільки п'ятизначних чисел можна записати за допомогою цифр 1, 2, 3, 4 і 5?»

За допомогою цифр 1 і 2 можна записати два двозначних числа: 21 і 12.

За допомогою трьох цифр 1, 2 і 3 можна записати тризначні числа: 123, 132, 213, 231, 312, 321.

А скільки ж тоді п'ятизначних чисел можна записати за допомогою цифр 1, 2, 3, 4 і 5? Звичайно, можна зробити, як і попередніх випадках: просто перебрати всі можливі варіанти, а як бути, якщо треба записати десятизначне число? Адже тут ми будемо змушені витратити дуже багато часу, щоб записати всі варіанти, та й нічого не пропустити й не записати двічі. Відповістити на запитання, і допоможе наша тема: «Перестановки».

                                            Це цікаво.

                                               Термін «перестановки» увів Я.Бернуллі в 1713 р.;

                            Знак факторіала був уведений в 1808 році в одному французькому підручнику Х. Крампа; позначення «0! = 1» увів в 1656 році Дж.Валлис в «Арифметиці нескінченних»; за рішенням англійської Академії наук «n!» читали «n захоплення».

Щоб відповістити на поставлене запитання нам довелося перебрати найрізноманітніші варіанти. Інакше кажучи, ми переставляли дані нам

елементи, утворюючи нові сполуки, які відповідали умові задачі. Такі сполуки носять певну назву - перестановки.

Перестановки – це сполуки з n елементів, які відрізняються між собою порядком елементів.

 Позначають перестановки так:  Р_n 

Як же підрахувати кількість перестановок з n елементів? 

         Давайте для того, щоб одержати формулу розглянемо кілька простих випадків. Нехай нам треба підрахувати кількість перестановок з 1 -го елемента, з 2-х, з 3-х, і т.д. елементів.

Якщо n =1, Р₁ = 1;                            

         n = 2, Р₂ = 2; дивися вище:  21 і 12;   

         n = 3, Р₃ = 6; дивися вище: 123, 132, 213, 231, 312, 321;

         n = 4, Р₄ = 24;  1234, 1243, 1324, 1342, 1423, 1432,

                                   2134, 2143, 2341, 2314, 2413, 2431,

                                   3124, 3142, 3214, 3241, 3421, 3412,

                                   4123, 4132, 4213, 4231, 4321, 4312.

        n = 5, Р₅ = ? Якщо міркувати аналогічно  з Р₄ , то зафіксуємо на першому місці цифру 1 і будемо переставляти інші чотири цифри, тобто ми одержимо 24 варіанта; далі – зафіксуємо на першому місці цифру 2 і знову переставляємо

4-ри цифри, які залишилися. І так  з іншими цифрами. У такий спосіб ми одержуємо п'ять рядків, у кожному такому рядку по 24 варіанта, усього 5^.24=120 різних перестановок. Р₅ = 120.

 Аналогічно, Р₆ = 720, Р₇ = 5040 і т.д.

Р_n = 1.2.3.4....^.(n – 1)^.n

Р_n = n!

Читається: « П із эн дорівнює эн факторіал».

Факторіал – це добуток всіх чисел від 1 до n включно.

 

Обчислити:

1. 6!=1 ^.2 ^.3^.4 ^. 5^.6=720;
2. 10!= 1 ^.2 ^.3^.4 ^. 5^.6 ^. 7^.8 ^.9 ^.10 = 3628800;
3. 12!=__________________________________________________________
4. 9! - 5! = _______________________________________________________

____________________________________________________________________________________________________________________________________

5. 5! + 7!=_________________________________________________________

____________________________________________________________________________________________________________________________________

Розв'язати задачі.

№1. Скільки різних шестизначних чисел можна записати, використовуючи цифри 1,2,3,4,5,0, якщо кожна цифра входить у запис числа тільки один раз? (якщо сам не зможеш, переверни сторінку, там є зразок розв'язку)

 

Зразок розв'язання: з даних шести цифр можна записати Р₆=6! шестизначних виразів. Але серед цифр є нуль, виходячи  із цього, треба виключити ті шестизначні вирази, у яких на першому місці записаний нуль, тому що це не буде шестизначним числом. А таких виразів буде Р₅=5!, тому що інші цифри можна переставляти. Отже, за допомогою цифр 1,2,3,4,50 можна записати

Р₆-Р₅ шестизначних чисел.

 Р₆-Р₅=6!-5!= 720 - 120=600.

Відповідь:600 чисел.

№2. Скількома способами можна розставити 7 книг з історії й 4 книги по біології так, щоб всі книги по біології стояли поруч?

(якщо сам не зможеш, переверни сторінку, там є зразок розв'язку)

 

Зразок розв'язку задачі №2: Об'єднаємо умовно всі книги з біології в одну. Тоді в нас буде 8 «книг» і їх можна розмістити Р₈=8! способами на поличці. Книги з біології «усередині» нової книги можна переставляти Р₄=4! способами. Усього, за правилом добутку, у нас вийде Р₈^.Р₄ способів.

Р₈^.Р₄=8!^.4!=40320^.24=967680

Відповідь:967680 способами.

 

Розв'язати задачі.

                                                     №1.

 Скільки різних п'ятизначних чисел можна записати, використовуючи цифри 1,2,3,4,5, якщо кожна цифра входить у запис числа тільки один раз?

 

                                                           №2.

 Скільки різних п'ятизначних чисел можна записати, використовуючи цифри 0,1,2,3,4, якщо кожна цифра входить у запис числа тільки один раз?

 

                                                                    №3.

 Скількома способами можна розставити 4 книги з алгебрі й 3 книги з геометрії так, щоб всі книги по геометрії стояли поруч?

                                                                 №4.

 На книжковій полиці міститься 30 томів енциклопедії. Скількома способами можна розставити їх так, щоб: а) том 1-ий та 2-ий стояли поруч; б) том 3 і 4 не стояли поруч?

 

                                 Щоб перевірити себе, дай відповідь на питання:                                    

 

1.Дай визначення перестановки з n елементів: ___________________________________________________________________________________________________________________________________________________________________________________________________________

2.Яким символом прийнято позначати перестановки?______________

3.Що таке факторіал? ________________________________________________

4.Як позначають факторіал?__________________________________________

5.Яка формула для підрахунку кількості перестановок з n елементів?

 

                                                  Завдання до дому.

Розв'язати задачі.

№1.

Скільки різних семизначних чисел можна записати, використовуючи цифри 1,2,3,4,5,6,7, якщо кожна цифра входить у запис числа тільки один раз?

 

№2.

 Скільки різних дев'ятизначних чисел можна записати, використовуючи цифри 0,1,2,3,4,5,6,7,8, якщо кожна цифра входить у запис числа тільки один раз?

 

№3.

 Скількома способами можна розставити 5 книг по літературі й 4 книги по географії так, щоб всі книги по літературі стояли поруч?

 

 

                                            Тема : Розміщення.

                              Розглянемо множину С={а,в}. Вона складається із двох

                         елементів а і в (до речі, що така множина?) Тоді із множини            

                          С можна утворити дві підмножини ( а це що таке?), які

                           містять  по одному елементу: А={a}, В={в}. Якщо до цієї

                           множини додати ще один елемент с, то С={а,в,с}. І із елементів цієї множини можна утворити три підмножини по одному елементу й шість упорядкованих підмножин, які містять по два елемента: {а},{в},{с},{а,в},{в,с},{а,с},{в,а},{в,с},{с,а}.

 Всі ці підмножини відрізняються друг від друга або елементами, або порядком їхнього запису.

Тоді, якщо задати собі те ж питання, що й при вивченні попередньої теми: а що, якщо множина складається з п'яти елементів?

Звичайно, можна зробити як і попередніх випадках: просто перебрати всі можливі варіанти, а як бути, якщо треба записати десятизначне число? Адже отут доведеться багато часу витратити, щоб записати всі варіанти, та й нічого не пропустити й не записати двічі.

 На що ще треба звернути увагу при цьому - на те, що при складанні підмножин у нас використовувалися не всі елементи даної множини

(згадаємо, що при перестановках використовуються всі елементи). Вирішити цю проблему допоможе наша нова тема: «Розміщення».             

Отже, якщо в нас є множина, що складається з n елементів, а ми використовуємо тільки m з них і при цьому групи елементів відрізняються

 друг від друга

принаймні одним елементом

або

порядком запису елементів

Значить ми одержали розміщення.

Розміщення – це сполуки із n елементів по m, які відрізняються друг від друга або складом елементів, або порядком запису елементів.

 

 Позначають розміщення: А 

 Як же знайти кількість розміщень із n по m.

Нехай ми маємо n елементів. Перший елемент можна вибрати n способами. Другий елемент доводиться вибирати з n-1 елементів, які залишилися, тому другий елемент можна вибрати вже n-1 способом. Тоді за правилом добутку таких наборів із двох елементів можна скласти n ^.( n-1) способами. Третій елемент ми будемо відбирати із числа n-2 елементів, які залишилися. Це можна зробити n-2 способами. Тоді трійки елементів можна утворити    

n ^.( n-1) ^.( n-2) способами, знову використовуючи правило добутку. Аналогічно, набір із чотирьох елементів можна вибрати n ^.( n-1) ^.( n-2) ^.( n-3) і т.д.

Значить із m елементів  можна вибрати n ^.( n-1) ^.( n-2) ^. … ^.( n-n-(m-1)) способами.

 Таким чином,

                                А = n ^.( n-1) ^.( n-2) ^. … ^.( n-n-(m-1)).

Помножимо й розділимо цю формулу на добуток

( n-m)( n-m-1)( n-m-2)…^. 3 ^.2 ^.1

Одержимо:

А = =

Тому

                                        А = n ^.( n-1) ^.( n-2) ^. … ^.( n-n-(m-1)).

або ж

                                            А =

 

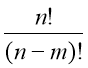
                          Задача №1.

 Розклад на день містить 5 уроків. Визначити кількість можливих розкладів на день при виборі з 11 дисциплін, за умовою, що кожний предмет не повинен бути в розкладі двічі.

Задача №2.

 Скільки різних тризначних  натуральних чисел можна скласти із цифр 1,2,3,4,5 за умови, що в кожне число входить кожна цифра не більше одного разу?

Задача №3.

 Скільки різних тризначних і чотиризначних  натуральних чисел можна скласти із цифр 1,2,3,4,5 за умови, що в кожне число входить кожна цифра не більше одного разу?

 

Задача №4.

Скільки різних тризначних  натуральних чисел можна скласти із цифр 0,1,2,3,4 за умови, що в кожне число входить кожна цифра не більше одного разу?

Задача №5.

Скільки різних натуральних чисел можна скласти із цифр 0,1,2,3,4 за умови, що в кожне число входить кожна цифра не більше одного разу?

 

                         Щоб перевірити себе, дай відповідь на питання:

 1.Дай визначення розміщення з n по m елементів: ___________________________________________________________________________________________________________________________________________________________________________________________________________

2.Яким символом позначають розміщення?______________

3.Що таке факторіал? ________________________________________________

4.Як позначають факторіал?__________________________________________

5.Яка формула для підрахунку кількості розміщення з n по m елементів? ______________________________________________________

                                              Завдання до дому.

Розв'язати задачі.

№1.

Скільки різних шестизначних натуральних  чисел можна записати, використовуючи цифри 1,2,3,4,5,6,7, якщо кожна цифра входить у запис числа тільки один раз?

 

 

№2.

 Скільки існує варіантів розсадити 6 учнів на 12 місцях? 

№3.

 Скількома способами можна присудити золоту, срібну, бронзову медаль у змаганнях, у яких беруть участь 15 спортсменів?

№4.

Скільки різних правильних дробів можна записати за допомогою чисел 3, 5,7,11,13,17,19,23, за умови, що в кожний дріб входить два числа?

                                                          Тема : Сполучення (комбінації).

                    Нехай у нас є коробка  з 4 відділеннями й 2 кульки,

        які в цю коробку треба покласти. Що нас буде цікавити?

                        Звичайно, є в коробці кулька чи ні, а те, у якому

відділенні і яка саме кулька в ньому лежить нас хвилювати не буде. Уявити собі це можна так:

 

Вийшло 6 варіантів. Але, знову таки, це, коли всього 2 кульки й 4 відділення в коробці. А якщо їх буде більше? Наприклад, розглянемо множину А={a,b,c,d}. Для нього можна скласти чотири підмножини по одному елементу; шість підмножин по два елемента; чотири підмножини, які містять по три елемента й одну підмножину, що містить всі чотири елементи. Разом одержуємо 15 різних підмножин. А чим же вони відрізняються? Кожні два з них мають по одному різному елементу.

На що ще треба звернути увагу при цьому - на те, що при складанні підмножин ми використовували не всі елементи даної множини (згадаємо, що при перестановках використовували всі елементи, а в розміщеннях ні).             

Отже, якщо в нас є множина, що складається з n елементів, а ми використовуємо тільки m з них і при цьому групи елементів відрізняються

принаймні одним елементом

то мова йде про   сполучення (комбінації).

Тому сполучення(комбінації ) - це

 

 Позначають сполучення: С 

 У кожному зі сполучень є m різних елементів, з яких можна отримати Р_m перестановок. Сукупність всіх таких вибірок, отриманих шляхом побудови всіх перестановок на базі кожного сполучення, являє собою число розміщень А ,

таким чином

А = С ^. Р_m ,  звідси маємо

                С =

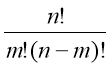
З огляду на те, що 0!=1, маємо

С=1   і  С=1. 

                              

                          Задача №1.

 З 20 працівників треба  вибрати шістьох для роботи на певній ділянці. Скількома способами це можна зробити?

Розв'язання: порядок вибору працівників не має значення, тому мова йде про кількість сполучень із 20 по 6, тобто

С == = =38760.

При розв’язанні цієї задачі ми насамперед звернули увагу на те,

що не важливий порядок відбору робітників, тобто це не розміщення, і не всі робітники будуть задіяні в роботі, тобто це не перестановки. Виходить перш ніж використовувати ту або іншу формулу, треба вибрати про які комбінації мова йде. У цьому нам допоможе алгоритм розв'язання комбінаторних задач.

                              Алгоритм розв'язку задачі (вибір формули).

                                         Чи враховується порядок

                              розміщення елементів?

 

                                            Так                                        Ні

 

 

          Чи всі елементи                                                                    Сполучення

          входять у сполуку?                                                С =

           Так                                        Ні

 

 

Перестановки                                                      Розміщення

        Р_n=n!                                                        А =

Використовуючи цей алгоритм, ми зуміємо набагато швидше розв'язувати задачі й робити при цьому менше помилок.

            Задача №2.

 На тренуваннях прийшли 12 баскетболістів. Скільки може бути утворено тренером різних стартових п'ятірок?

Розв'язання: чи враховується порядок  розміщення елементів?

Ні, тому що при складанні стартової п'ятірки тренера цікавить тільки її склад. Значить мова йде про сполучення (дивися алгоритм).

С = = = =792.

Задача №3.

 Для польоту на Марс необхідно укомплектувати екіпаж космічного корабля таким чином: командир корабля, перший його помічник, другий помічник, два бортінженери й один лікар. Командирська трійка повинна бути відібрана з 25 льотчиків, що готуються до польоту, два бортінженери - із числа 20 фахівців, і лікар - із числа 8 медиків. Скількома способами можна укомплектувати екіпаж дослідницької експедиції?

 Розв'язання:

Перше - при виборі командира і його помічників важливо визначити, який з військових льотчиків краще ніж інші справляється з тими або іншими функціями в управлінні корабля. Значить важливий не тільки склад, але відповідне розміщення людей, дивися алгоритм: чи враховується порядок  розміщення елементів? Так. Але тому що не всі елементи використовують, тому ця трійка може бути укомплектована А = способами.

Друге – обов’язки в бортінженерів приблизно однакові. Вони можуть виконувати їх по черзі. Отже, чи враховується порядок  розміщення елементів? Ні, тому пари бортінженерів може бути укомплектована

З = способами.

Третє – з лікарем. Аналогічно його можна підібрати З = способами.

У силу правила добутку весь екіпаж може бути підібраний

 А. С. З = 20976000 способами.

Задача №3.

 Скількома способами можна вибрати 3 ручки й 2 олівця з 6 різних олівців і 8 різних ручок?

Задача №4.

 Збори з 40 чоловік вибирають голову, секретаря й, разом, трьох членів комісії. Скількома способами це можна зробити?

 

 

                         Щоб перевірити себе, дай відповідь на питання:

 1.Дай визначення сполучень із n по m елементів: ___________________________________________________________________________________________________________________________________________________________________________________________________________

2.Яким символом позначають сполучення?______________

3.Що таке факторіал? ________________________________________________

4.Як позначають факторіал?__________________________________________

5.Яка формула для підрахунку кількості розміщення з n по m елементів? ______________________________________________________

6.Яка формула для підрахунку кількості сполучень  із n по m елементів? ______________________________________________________

6.Яка формула для підрахунку кількості перестановок з n елементів? ______________________________________________________

                                            Завдання до дому.

Розв'язати задачі.

№1.Скільки можна скласти різних нескоротних дробів, чисельником і знаменником яких є числа 2, 3, 5, 7, 11, 13, 17, 19?

№2.На площині обрані 10 точок. Скільки існує трикутників з вершинами в цих точках?

№3. У коробці лежать пронумеровані 6 білих і 8 чорних кульок. З коробки дістали 5 кульок ( без повернення). Скільки існує способів витягти: а) п'ять чорних кульок; б) хоча б одну білу кульку?

                                Тема : Розв'язання задач. Трикутник Паскаля.

                     Давайте довідаємося, з яким настроєм ви прийшли на урок.

                               Перед тобою сонечко, намалюй його личенько відповідно до 

                                твого настрою.

 

 

 

Оціни самостійно свою готовність до уроку.

Всі правила й формули, вивчені до сьогоднішнього уроку я знаю на ______________.

Ці правила й формули я ______________застосовувати при рішенні задач.

Як же вирішити задачу по комбінаториці? Щоб відповісти на це питання,  склади алгоритм розв'язку за допомогою блоків.

Що означають символи на блоках?

За допомогою якої формули розраховують кількість комбінацій?

_______________________________________________________________

Розв'язати задачі:

№1.

Скількома способами можна розмістити на поличці 5 томів одного письменника так, щоб вони не були розташовані один за іншим у послідовності зростання їхніх номерів?

№2.

На площині обрані 12 точок. Скільки існує трикутників з вершинами в цих точках?

№3.

Скільки різних цілих тризначних чисел можна скласти із цифр  1,2,3,4,5,6,7,8,9 так, щоб цифри в числі не повторювалися? 

 

                                               Історична довідка.

                                       Як сказав один з відомих математиків 16 ст. Стевин :

                        «Серед чисел існує така досконалість і згода, що нам треба міркувати дні  й ночі над їхньою дивною закономірністю».

Ще в Древньому Китаї й Древній Греції захоплювалися тим, що складали магічні квадрати із чисел. В 16-17 століттях, коли відбувалося зародження й становлення комбінаторики як науки, до цього знову звернулися вчені й от

про одне із їхніх надбань ви сьогодні й довідаєтеся. Названо воно на честь одного з авторів Блеза Паскаля

                                                            Обчислити:

                                  і  ;   і ;  і  .

                     Про яку формулу-властивість нам тут нагадали?

      Давайте зрівняємо, наприклад, попередньо

       виконавши обчислення.

                     і ;    і ;   і                                                      

Який висновок можна зробити?                                                                    

________________________________________________

Якщо не помітили закономірності, то відповіси на запитання:

Що загального в С ліворуч і праворуч?

Чим вони відрізняються?

Як зв'язані числа верхнього індексу?

А тепер я вам пропоную записати це трохи інакше, обчисливши усно:

 

n=0                                           ____________________________                                         

n=1                                                       ____________________________

 

n=2                                               _____________________________

 

n=3                                                                     _____________________________

 

На що схожий наш запис? __________________________,

який і назвали на честь Паскаля -  _________________ Паскаля, тому що він одержав більшу популярність після робіт цього вченого. Але частково цей _____________________був відомий ще  в 2 столітті до нашої  ери в Індії, до n=8 він приводиться в трактаті «Дзеркало чотирьох елементів» китайського математика Чжу Ши-Цзе 13-14 століття, а в Європі до Паскаля він фігурує в працях Апіана (1527р.) і Штіфеля (1544р.)  А який буде в ньому наступний рядок?

n=4       __________________________

Записати його дуже просто, помітивши, що нижнє число дорівнює сумі двох чисел, які розташовані над ним.

А якщо я запропоную вам записати властивість для n-ой рядка, ви самостійно зможете  його записати в  загальному вигляді?

____________________________________________________________________

 

А тепер звернемося  до алгебри? Вивчали тему «Формули скороченого множення»? А якщо виписати числові коефіцієнти в них, що ми одержимо?

(a+b)⁰=1       1

(a+b)¹=a+b                      1       1 

(a+b)²=a²+2ab+b²                                            1      2       1

Знову з'являється ___________________Паскаля.

Перевіримо для n=3 (розкриваємо дужки на  дошці). Одержали

(a+b)³=_________________________________________

 

 

                                                        Це цікаво.

                         Отож цей ______________________Паскаля допомагає            

                    піднести (а+в) у  будь-який степень, а побачив це Ньютон.     

                     Тому біном Ньютона - це формула  скороченого множення для будь-якого степеня. До речі, про це задовго до Ньютона знав азіатський учений і поет Омар Хайям, ще в 12 столітті. З його  літературною спадщиною ви познайомитеся на уроках літератури, але його докладного опису бінома не збереглося. 

В 1265 р. інший учений Азії Ат-Туси написав книгу, що дійшла до наших днів, в якій наведені формули до n=12 включно.

                                       Дай відповідь на питання:

                 Із чим ми сьогодні познайомилися?

                 Які нові формули одержали?

                 Що нового довідалися?

 

                                              Завдання до дому:

                           Вивчити теоретичні відомості по конспекту, продовжити трикутник Паскаля до n=12.

                                               Тема : Трикутник Паскаля. Біном Ньютона.

                            Давай ненадовго відволічемося від комбінаторики ( а, до речі,

                           ти не забув, що вивчає цей розділ математики? Якщо забув,

                           повернися й повтори.) і згадаємо нашу алгебру. Конкретно

                            теми «Степень» і «Формули скороченого множення».

                                       (а+b)⁰=1;

                                       (а+b)¹=a+b;

                                       (а+b)²=a²+2ab+b²;                                                

                                       (a+b)³=a³+3a²b+3ab²+b³;

 Давайте ми з вами зараз продовжимо обчислення ступенів бінома

( вираження а+b, як і взагалі будь-який двочлен, називається біномом) і знайдемо ще, наприклад, розкладання четвертого й п'ятого ступенів:

(а+b)⁴=(а+b)³(а+b)=____________________________________________________________________________________________________________________________________________________________________________________________

(а+b)⁵=(а+b)⁴(а+b)=________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Підсумок

(а+b)⁴=______________________________________________________________

(а+b)⁵=______________________________________________________________

 Розглядаючи ці формули й порівнюючи коефіцієнти із трикутником Паскаля, можна помітити, що вони _____________________________________.

Це не випадково. Твердження це було доведено, а ми, поки що, змушені будемо прийняти його на віру. Формулу називають біномом Ньютона на честь відомого англійського математика й фізика Ісаака Ньютона.(див. таблицю)

 

 

 

n       коефіцієнти                                                                      коефіцієнти                    n

0          1                                                                                                           1                 0 1          1  1                     (a+b)1=C a+C b;                                             C  C               1 2          1  2   1                (a+b)2=C a2+C ab+C b;                           C C C            2 3          1  3   3  1            (a+b)3=C a3+C a2b+C ab2+C b3         C C C C            3 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -                 (a+b)n = C an+ C an-1b+ C an-2b2+ C an-3b3+…+Cabn-1+Cbn

  Числа C , C ,  C , C ,…,C,Cназивають біноміальними коефіцієнтами.

Для їхнього обчислення, як ти, напевно, уже зрозумів по позначеннях, використовують формулу сполучень.

 Підрахуй у розкладанні бінома Ньютона кількість доданків.

Виходить, що в розкладанні бінома міститься ___________________________

____________________________________________________________________

Всі члени розкладання відносно a і b мають один й той же вимір, рівний показнику степеня бінома. ( Виміром одночлена щодо  змінних a і b називається сума показників степенів даних змінних, які входять до цього одночлену).

Також можна помітити, що показник степеня a, починаючи з n _____________,

а показник ступеня b, починаючи  з 0____________________________________

Розрізняється розкладання бінома й за парністю степеня:

якщо показник n=2k, то середній член розкладання найбільший;

якщо показник n=2k-1, то існують два «середніх» члени розкладання з однаковими найбільшими біноміальними коефіцієнтами.

 Давай зрівняємо коефіцієнти  членів розкладання, рівновіддалених від кінців ряду. Вони між собою ________________________________________.

Це можна записати в загальному вигляді ( спробуй зробити це сам, якщо не виходить переверни сторінку).

________________________________________________________________________________________________________________________________________

 Формула Т_k+1=Ca^n-k b^k  називається формулою загального члена розкладання, тому що, надаючи змінної k цілі значення від 0 до n, ми можемо одержати з її будь-який член розкладання.

 Ще одна цікава властивість: виявляється, сума всіх біноміальних коефіцієнтів розкладання будь-якого ступеня n дорівнює 2ⁿ.

Приклад:

Знайти розкладання (3х-2)⁵.

(3х-2)⁵ = C (3х)⁵ + C (3х)^{4 .} (-2) + C (3х)^{3 .}(-2)² + C (3х)^{2 .} (-2)³ +C (3х)^.(-2)⁴+ +С.(-2)⁵=243х⁵ - 810х⁴ + 1080х³ - 720х² + 240х – 32.

                                   Дай відповідь на питання:

              Із чим ми сьогодні познайомилися?

             Які нові формули одержали?

             Які цікаві властивості має біном Ньютона?

  У загальному виді властивість рівності коефіцієнтів записується так:

                                                         С =С

 

                                                Завдання до дому:

                                       №1.

 Розкласти по формулі бінома Ньютона:

1) ( x-y)⁵;

2) (2x+y)⁴;

3) (3 x-2y)⁶;

4) ( +4)⁵;

5) ( - )⁸;

6) ( +х)⁴.

                                      №2.

Знайти член розкладу ( х- )⁹, який не містить х.

                                      №3.

Знайти п'ятий член розкладу (2х-4у)⁶.

 

                                         Тема : Розв'язок задач.

                                            Настав час застосовувати всі отримані знання на

    практиці. При розв'язанні задач тобі  треба ретельно вибирати

                             тип комбінацій, щоб вибрати потім формулу для розрахунку

                             їхньої кількості. У цьому тобі допоможе  алгоритм розв’язання задач.

                              Алгоритм розв’язання задачі (вибір формули).

                                          Чи враховується порядок

                              розміщення елементів?

 

                                            Так                                        Ні

 

 

          Чи всі елементи                                                                    Сполучення

          входять у сполуку?                                                С =

           Так                                        Ні

 

 

Перестановки                                                      Розміщення

        Р_n=n!                                                        А =

 

 

 

 

 

 

 

 

 

Задачі.

Група А.

№1.

Скількома способами можна скласти список з 15 предметів?

№2.

Скількома способами можна розставити на поличці 5 томів одного автора так, щоб вони не були розставлені в порядку зростання їхніх номерів?

№3.

Скільки кольорів можна одержати, змішуючи основні сім кольорів?

№4.

У ящику знаходяться 6 білих і 8 чорних кульок. З ящика навмання виймають 5 кульок ( без повернення). Скількома способами можна вийняти: а) чотири білих кульки; б) хоча б одну чорну кульку?

№5.

На десяти картках записані цифри 0,1,2,3,...,8,9 ( на кожній картці по одній цифрі). Беруть чотири картки й складають з цифр, записаних на них чотиризначне число. Скільки різних чотиризначних чисел можна одержати в такий спосіб?

№6.

Розклади: а) (2х+5)⁶; б) (3у-4х)⁹.

Група Б.

№1.

Є 10 тюльпанів, 25 білих і 15 жовтих  нарцисів. Скількома способами можна скласти букет, у якому 5 тюльпанів і по 2 нарциси кожного кольору?

№2.

Скільки парних п'ятизначних чисел можна записати за допомогою цифр 2,3,4,5,9?

№3.

Серед 25 чоловік, з них 10 дівчин, розігрують 5 квитків на шоу. Скільки існує способів виграшу цих квитків 2 дівчинами й 3 юнаками?

№4.

Складені розміщення з 10 елементів по 7. Скільки із цих розміщень: а) містять заданий перший елемент; б) не містять заданий перший елемент?

№5.

В автомобілі є 7 місць, включаючи місце водія. Скількома способами 7 чоловік можуть сісти в автомобіль, якщо місце водія можуть зайняти тільки троє з них?

№6.

Знайти х, якщо п'ятий член розкладання ( х-₂)⁶ дорівнює .

Група В.

№1.

Скількома способами із цифр 1,2,3,4,5,6.7,8,9, можна скласти шестизначні числа, у яких цифри не повторюються, але обов'язково присутні в запису цифри 1,2,3?

№2.

З 3 інженерів і 9 економістів повинна бути створена комісія в складі семи чоловік. Скількома способами її можна створити за умови, що до неї обов'язково входить хоча б один інженер?

№3.

З 10 троянд і 8 жоржин треба скласти букет, у якому буде не менше 8 троянд і 7 жоржин. Скількома способами можна скласти такий букет?

№4.

Серед чотирьох гравців у доміно нарівно треба розподілити 28 кісточок доміно. Скількома способами це можна зробити?

№5.

З 10 спортсменів, серед яких 2 велосипедиста, 3 плавця, а інші - легкоатлети, треба скласти команду, у яку б увійшло не менше одного спортсмена кожного виду спорту. Скількома способами це можна зробити, якщо в команді повинно бути 6 спортсменів?

 

№6.

Знайти середній член розкладу (-      )¹⁶.

 

                                       Тема : Розміщення з повтореннями.

                                        Настав час поговорити про випадки, коли

                                        елементи в сполуках повторюються.

                                       Генеральна сукупність із повтореннями – це набір

                                     елементів n різних класів, коли елементи, які належать

 одному класу, вважаються однаковими.

                 ,…,

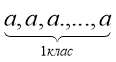
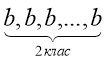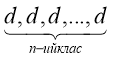
Число елементів у кожному із цих класів необмежене.

 Вибіркою з повтореннями об'єму m будемо називати довільну групу m елементів генеральної сукупності з повтореннями.

Наочно це можна представити як стрічку, складену з n фігурок, цього разу стрічка може бути не тільки строкатої. Незалежно від m вона може бути й одноколірної.

 

- без повторень

 

                                                                                        - з повтореннями.

                                       

Якою мінімальною ознакою може відрізнятися одна така вибірка від іншої вибірки такого ж об'єму? Простіше кажучи: якою мінімальною ознакою можуть відрізнятися візерунки стрічок, побудованих з однакової кількості фігурок? Іншим фарбуванням принаймні одного квадрата або порядком розташування квадратів у лінійному ладі.

Тобто одна вибірка може відрізнятися від інший

або

принаймні одним елементом

або

порядком розташування елементів.

Ці ознаки збігаються з ознаками, по яких одні розміщення відрізняються від інших. Тому вибірки, про які зараз мова йде, називаються

розміщення з повтореннями з елементів n класів по  m.

 

 Позначають розміщення з повтореннями: 

 Як же знайти кількість розміщень із n по m.

Перший елемент згаданих розміщень  можна вибрати n способами: деякий елемент кожного з n класів. Другий елемент вибирається теж n різними способами: знову деякий елемент кожного з n класів. За  правилом добутку розміщення об'єму 2 можна вибрати n ^. n = n²  різними способами. Третій елемент можна вибрати теж n  способами: знову деякий елемент  кожного з n класів. Тоді розміщення об'єму 3 можна вибрати в силу правила добутку n^{2 .} n = n³ . У такий спосіб розміщення об'єму m можна побудувати n^m різними способами.

                                            =n^m

                            Задача №1.

       Автомобільний номер складається із трьох літер і чотирьох цифр.

Знайти кількість всіх можливих номерів, якщо використовують 32 літери російського алфавіту?

Розв'язання: Тому що літери й цифри в номері можуть повторюватися, маємо:

кількість способів набору літер = 32³;

кількість способів набору цифр = 10⁴;

Тоді кількість різних автомобільних номерів за правилом добутку

дорівнює ^.= 32^3. 10⁴=327680000.

Задача №2.

 Скільки чотиризначних чисел можна записати за допомогою цифр 1, 2, 3, 4, 5, 6, 7, 8.9, якщо цифри в записі числа можуть повторюватися?

Задача №3.

 Скільки різних п'ятизначних чисел можна записати цифрами 1, 2, 3, якщо цифри в записі можуть повторюватися?

Задача №4.

 Скільки різних чотиризначних чисел можна записати цифрами 0, 1, 2, якщо цифри в записі можуть повторюватися?

 

 

 

Завдання до дому:

Задача №1.

 Шість школярів здають іспити. Скільки може бути варіантів розподілу оцінок, якщо вони одержали бали високого рівня (10, 11, 12)?

Задача №2.

 У ліфт 9-поверхового будинку зайшли на першому поверсі шість чоловік. Скількома способами вони можуть вийти з ліфта?

 

                           Тема : Сполучення й перестановки з повтореннями.

                                        Із всієї сукупності розміщень із повторенням

 можна виділити групу вибірок з повтореннями, котрі          

 відрізняються друг від друга принаймні одним 

елементом. Це, по-перше, а, по-друге, порядок розташування елементів у ряді випадків не приймається в увагу.

Такі розміщення з повтореннями прийняти називати сполучення з повтореннями.

Сполучення з повтореннями  з n класів  по m називаються такі розміщення з повтореннями з n класів  по m, які відрізняються друг від друга хоча б одним елементом.

 Позначають такі сполучення:  

Для знаходження кількості сполучень із повтореннями використовують формулу:

   =С

Задача №1.

 Скільки різних букетів, що складаються з 9 квіток, можна скласти , якщо в продажі є квіти п'яти сортів?

Розв'язання: з п'яти сортів треба вибрати дев'ять квіток - це значить, перші п'ять квіток будуть різні, а потім вони почнуть повторюватися.

Тому  = = С = =143.

Задача №2.

Скільки різних семизначних чисел можна записати за допомогою трьох одиниць, двох двійок і двох трійок?

Розв'язання: семизначне число за допомогою тільки трьох цифр записати

 не можна, виходить, цифри повинні в запису числа повторюватися. Але одне записане семизначне число в цьому випадку відрізняється від іншого порядком

проходження цифр, отже, мова йде про перестановки,

але не звичайні, а з повтореннями.

Перестановки з повтореннями по k елементів  з n різних  класів   називаються  розміщення з повтореннями об'єму k,  які відрізняються друг від друга тільки порядком розташування елементів, коли від i-го класу в кожній вибірці бере участь k елементів.

 

Позначають такі сполуки: P_{k ,k ,…,k}

Формула для знаходження кількості перестановок з повтореннями має вигляд:

           P_{k ,k ,…,k}=                       ,де k=k₁+k₂+…+k_n...

Тоді  Р_3,2,2= = = 210, де врахували, що 3+2+2=7.

Задача №3.

 Скільки різних «слів», у тому числі й безглуздих, можна одержати, переставляючи літери в слові: а) математика; б) паралелограм; в)однокласники?

Задача №4.

Скількома способами можна скласти набір з 7 тістечок, якщо в продажі  є тістечка 4 сортів?

Задача №5.

У продаж надійшли листівки 12 різних видів. Скількома способами можна утворити набір з 20 листівок? З 10 листівок?

                                              Тема : Практикум по розв'язанню задач.

Ми багато чого довідалися за цей час. Прийшов час для розв'язання комбінаторні задачі, які вимагають всіх наших знань і вмінь. Тому, повторивши  необхідні формули, відправимося уперед.

 

 

Дай відповідь на питання:

1.Що таке перестановки?

2.Дай визначення розміщенням?

3.Що називається сполученнями?

4.Що розуміють під символом n!?

5. Чому дорівнює 0!, 1! ?

6. За якими формулами знаходять кількість перестановок, розміщень, сполучень?

7.Чим відрізняються розміщення від сполучень?

8.Чим відрізняються перестановки від розміщень і сполучень?

9.Як будується кожний наступний ряд у трикутнику Паскаля?

10.Якими властивостями володіють біноміальні коефіцієнти?

11.Чому дорівнює сума всіх біноміальних коефіцієнтів розкладу?

12. Запиши розклад бінома Ньютона.

13.Як записується загальний член розкладу?

14.Як змінюються показники степенів у розкладі бінома?

15.Поясни, що таке розміщення з повтореннями.

16.Що таке перестановки  з повтореннями?

17. Дай визначення, що називається сполученнями з повтореннями.

18. За якими формулами знаходять кількість розміщень із повтореннями? сполучень із повтореннями? перестановок з повтореннями?

19.Пригадай алгоритм розв'язання комбінаторних задач.

Тепер уперед.

Задачі.

№1.

 Із цифр 1, 2, 3, 4, 5 складають різні тризначні й чотиризначні числа. Скільки таких чисел можна скласти, якщо цифри в них не повторюються?

№2.

 Складені розміщення з 10 елементів по 7 елементів. Скільки із цих розміщень: а) містять заданий другий елемент; б) не містять заданий другий елемент?

№3.

 Скільки парних п'ятизначних чисел можна записати за допомогою цифр 2, 3, 4, 5, 7?

№4.

На футбольний турнір треба послати збірну команду в складі: тренер, його помічник, 2 асистента, 20 футболістів, лікар і 2 масажисти. Тренерський склад може бути обраний з 10 фахівців, футболісти - з 25 спортсменів, лікаря можна вибрати одного із трьох, а масажиста - двох з п'яти претендентів. Скількома способами може бути укомплектована така команда?

№5.

 У їдальні в меню є 4 перші блюда, 5 других і 3 третіх. Скількома способами можна вибрати собі обід із трьох блюд так, щоб у ньому було й перше, і друге, і третє?

№6.

 Скількома способами за допомогою цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, можна записати шестизначні числа з різних цифр, у записі яких є цифри 1, 2, 3?

№7.

 На конкурс по заміщенню вакансій у відомій компанії надіслали анкети 10 бухгалтерів і 8 менеджерів. Скількома способами можна прийняти на роботу трьох фахівців так, щоб серед них був хоча б один бухгалтер і хоча б один менеджер?

 

№8.

 На іспиті задається 10 питань, з яких 3 питання по математиці. Скількома способами можна задати ці питання так, щоб питання по математиці не були задані підряд?

№9.

 Дано дві паралельні прямі. На одній обрано 6 точок, на іншій - 8 точок. Скільки існує трикутників з вершинами в цих точках?

№10.

 З 10 різних троянд і 8 різних жоржин треба скласти букет, у якому буде не менше 5 троянд і не менше 3 жоржин. Скількома способами це можна зробити?

Короткі відомості по курсу «Комбінаторика».

1.Комбінаторика - розділ математики, у якому для кінцевих множин розглядають різні сполуки (комбінації) елементів.

2.Правило суми:

Якщо елемент А можна вибрати n способами, а елемент В m способами, то « або А або В» можна вибрати n+m способами.

 Інакше кажучи, сполучник «АБО» означає додавання.

3.Правило добутку:

Якщо елемент А можна вибрати n способами, а елемент В m способами, то «А і В» можна вибрати nm способами.

 Інакше кажучи, сполучник «І» означає множення.

4. Перестановки – це комбінації з n елементів, які відрізняються друг від друга порядком запису елементів.

 Позначають перестановки так:  Р_n 

Р_n = 1^.2^.3^.4^....^.(n – 1)^.n

Р_n = n!

Читається: « П з эн дорівнює эн факторіал».

Факторіал – це добуток всіх чисел від 1 до n включно.

5. Розміщення - це комбінації з n елементів по m, які відрізняються друг від друга або складом елементів, або порядком їхнього  запису.

Позначають розміщення: А А =

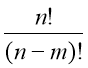
6. Сполучення - це  комбінації з n елементів по m, які відрізняються друг від друга складом елементів.

Позначають розміщення: С             С =

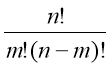
7. Розміщення з повтореннями  з n класів  по m називаються такі розміщення з повтореннями з n класів  по m, які відрізняються друг від друга або 

порядком розташування елементів, або хоча б одним елементом.

 = n^m           

8. Сполучення з повтореннями  з n класів  по m називаються такі розміщення з повтореннями з n класів  по m, які відрізняються друг від друга хоча б одним елементом.              Позначають такі сполучення:              

=С

9.Перестановки з повтореннями по k елементів  з n різних  класів   називаються  розміщення з повтореннями об'єму k,  які відрізняються друг від друга тільки порядком розташування елементів, коли від i-го класу в кожній вибірці бере участь k елементів. Позначають такі сполучення: P_{k ,k ,…,k}

P_{k ,k ,…,k}=,де k=k₁+k₂+…+k_n...

10.Біном Ньютона:

(a+b)ⁿ = C aⁿ+ C an-1b+ C an-2b²+ C an-3b³+…+Cab^n-1+Cbⁿ

11...Алгоритм розв'язання задачі (вибір формули).

                                         Чи враховується порядок

                              розміщення елементів? 

  

                                            Так                                        Ні

 

 

          Чи всі елементи                                                                    Сполучення

          входять у сполуки?                                                З =

           Так                                        Ні

 

 

Перестановки                                                      Розміщення

        Р_n=n!                                                        А =