Мала академія наук України "Теорема Безу"

ЗМІСТ

1.	Вступ
2.	Квадратні рівняння ………………………………………………..		4
	2.1	Розв’язування квадратних рівнянь за допомогою дискримінанту ……………………………………………...	4
	2.2	Пряма та обернена теорема Вієта …………………………	5
3	Теорема Безу та її наслідки ………………………………………		9
	3.1.	Життєвий та творчий шлях Етьєна Безу ………………….	9
	3.2.	Теорема Безу …………………..………….……….……….	10
	3.3.	Наслідки з теореми Безу ………………………..………….	11
	3.4	Приклади застосування теореми Безу …………………….	13
4.	Висновки ………………………………………………………..…		18
	Перелік використаних джерел ………………………..……….…		19

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

Про математику, її історію, особливості, неповторну красу можна говорити нескінченно. Любов до цієї науки стає ще більше, коли побачиш не тільки саму науку, а й тих, хто цілком присвятив себе великій справі і висвітлював в ній шлях далеко вперед.

Творці науки – це люди, що відрізняються винятковою цілеспрямованістю, відданою працею, відповідальністю перед людством за результати своїх досліджень. Творці математики – це люди з дивовижними долями, з сильними характерами, котрі долають труднощі і негаразди.

Важко розв'язувати рівняння третього степеня і вище. Розкладання лівої частини рівняння на множники, якщо права частина дорівнює нулю, – найпоширеніший метод вирішення самих різних рівнянь. Тут немає загальних рецептів. Багато чого залежить від уміння, кмітливості, спостережливості і досвіду.

Але такі рівняння не завжди можна розкласти на множники. Одним з методів, які допомогли вирішувати рівняння високих степенів, є теорема Безу.

Методи вивчення: опрацювання джерел інформації про вклад ученого в розвиток математики, теорема Безу та її наслідки.

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2

КВАДРАТНІ РІВНЯННЯ

2.1 Розв’язування квадратних рівнянь за допомогою дискримінанту

Квадратним рівнянням називається рівняння вигляду

ax² + bx + c = 0 (a0),    (2.1.1)

де х – змінна, a, b, c – деякі числа, причому

Числа a, b, c називають коефіцієнтами квадратного рівняння: а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член.

Якщо , рівняння називається зведеним квадратним рівнянням. Наприклад: x² – 6x + 1 = 0.

Якщо , рівняння називається не зведеним квадратним рівнянням. Наприклад: 3x² – 8x + 15 = 0.

Якщо у квадратному рівнянні хоча б один із коефіцієнтів b або с дорівнює 0, то таке рівняння називається неповним квадратним рівнянням.

Наприклад:  x² + 15 = 0.

Способи розв’язування неповних квадратних рівнянь:

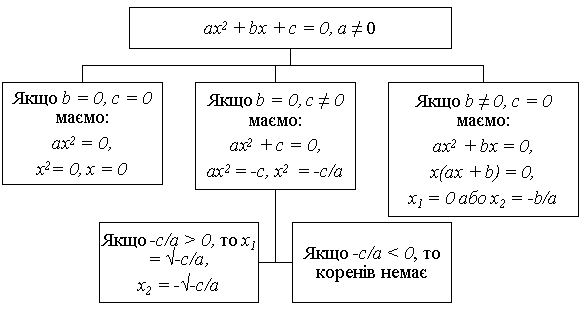
Розглянемо повне квадратне рівняння ax² + bx + c = 0 (a0). Корені даного рівняння знаходять за формулою:

          (2.1.2)

Вираз b² – 4ac називається дискримінантом і позначається літерою D.

1. Якщо D < 0, рівняння не має дійсних коренів.

2. Якщо D = 0,  рівняння має один корінь:

     (2.1.3)

3. Якщо D > 0, рівняння має два корені:

    (2.1.4)

Для квадратних рівнянь із парним другим коефіцієнтом зручніше користуватися формулою:

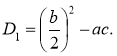    (2.1.5)

Тоді для , маємо

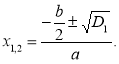     (2.1.6)

Наприклад:

1. Знайти корені квадратного рівняння

• x² – 26x + 120 = 0

D = 26² – 4·120·1 = 676 – 480 = 196 > 0 – рівняння має два корені

,

• 9x² – 12x + 4 = 0.

D = (-12)² – 4·9·4 = 144 – 144 = 0 – рівняння має один корінь

• x² + x + 6 = 0.

D = 1² – 4·6·1 = 1 – 24 = – 23 – рівняння не має дійсних коренів

2.2 Пряма та обернена Теорема Вієта

Теорема Вієта – формули, що виражають коефіцієнти многочлена через його корені. Ці формули зручно використовувати для перевірки правильності знаходження коренів та для задання многочлена з визначеними властивостями.

Теорема Вієта: Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів дорівнює вільному члену.

Доведення теореми:

Нехай х₁ та х₂ – корені зведеного квадратного рівняння x² + px + q = 0, дискримінант якого D = p² – 4q.

Якщо D > 0, то рівняння має два корені:

  та     (2.2.1)

Якщо D = 0, то рівняння має два однакових корені:

      (2.2.2)

Знайдемо суму та добуток коренів:

  (2.2.3)

  (2.2.4)

Отже, ; . Теорему доведено.

Використовуючи теорему Вієта, можна записати відповідні формули і для коренів будь-якого незведеного квадратного рівняння ax² + bx + c = 0 (a0).

Оскільки a0, поділимо обидві частини рівняння на а. Одержимо зведене квадратне рівняння:

     (2.2.5)

Тоді за теоремою Вієта:

;     (2.2.6)

Наприклад:

1. Не розв’язуючи рівняння 3x² – 5x – 7 = 0, знайдіть суму та добуток його коренів.

Розв’язування: Знайдемо дискримінант рівняння, щоб пересвідчитись, що корені існують: D = 5² – 4·3·(-7) > 0 – рівняння має два корені х₁ та х₂. Отже, за теоремою Вієта:

; 

Відповідь: та .

2. Один із коренів рівняння x² + рx – 18 = 0 дорівнює 3. Знайдіть коефіцієнт р та другий корінь рівняння.

Розв’язування: Нехай х₁ = 3 – один із коренів рівняння, а х₂ – другий його корінь. За теоремою Вієта: ;  . Ураховуючи, що х₁ = 3, маємо:

     

Відповідь: , .

Теорема, обернена до теореми Вієта: Якщо деякі два числа m і n такі, що їхня сума дорівнює другому коефіцієнту зведеного квадратного рівняння, узятому з протилежним знаком, а їхній добуток дорівнює його вільному члену, то дані числа є коренями цього зведеного квадратного рівняння x² + px + q = 0.

Доведення оберненої теореми:

За умовою ; . Тому рівняння x² + px + q = 0 можна записати наступним чином:

x² – (m + n)x + mn = 0.

Перевіримо, чи є число m коренем цього рівняння, для цього підставимо в ліву частину рівняння замість змінної х число m. Одержимо:

m ² – (m + n)m + mn = m ² – m² – nm + mn = 0.

Отже, m – корінь цього рівняння.

Аналогічно, підставимо в ліву частину рівняння замість змінної х число n. Одержимо:

n ² – (m + n)n + mn = n ² – n ² – nm + mn = 0,

тобто n – також корінь цього рівняння.

Отже, m і n – корені рівняння x² + px + q = 0, що й треба було довести.

Під час розв'язування треба також враховувати такі висновки з теореми Вієта:

1.  Якщо q < 0, х₁ і х₂ мають різні знаки.
2.  Якщо q > 0, х₁ і х₂ обидва від'ємні чи обидва додатні. Знак суми х₁ і х₂ є протилежним до знаку р.  

Наприклад:

1. Складіть зведене квадратне рівняння, коренями якого є числа -5 та 2.

Розв’язування: Шукане квадратне рівняння має вигляд x² + px + q = 0. За теоремою, оберненої до теореми Вієта:

p = – (х₁ + х₂) = – (–5 + 2) = 3

q = х₁ · х₂ = –5 · 2 = –10.

Отже,  x² + 3x – 10 = 0 – шукане рівняння.

Відповідь: x² + 3x – 10 = 0

2. Розв’яжіть рівняння: х² – 8х – 9 = 0.

За теоремою Вієта: х₁ х₂ = – 9;  х₁ +  х₂ = 8;  9 = 1 ^. 9 = 3 ^. 3. Очевидно, що                  8 = 9 + (-1).

Відповідь: х₁ = -1; х₂ = 9.

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 3

ТЕОРЕМА БЕЗУ ТА ЇЇ ЗАСТОСУВАННЯ

3.1 Життєвий та творчий шлях Етьєна Безу

Етьєн Безу (фр. Etienne Bezout) – французький математик, член Паризької Академії Наук (з 1758 року) народився 31 березня 1730 року в Немурі, Франція. Життя його сім’ї було пов’язане з політикою, його батько і дід служили в якості окружних суддів. Замість того, щоб слідувати їх прикладу, Безу, на якого у ранньому віці вплинув Леонард Ейлер, вибрав кар’єру математика.

У віці 28 років, Безу став членом Паризької Академії Наук. З 1763 року викладав математику в училище гардемаринів, а з 1768 року почав працювати з кандидатами в артилерійські офіцери.

Основні роботи Етьєна Безу відносяться до вищої математики, вони присвячені створенню теорії розв’язання алгебраїчних рівнянь. У теорії розв’язання систем лінійних рівнянь він сприяв виникненню невідомих з систем рівнянь вищих степенів, довів теорему (вперше сформульовану К. Маклореном) про те, що дві криві порядку m і n перетинаються не більше ніж в mn точках.

Багато сучасників захоплювалися Безу, його вмінням просто пояснювати складні питання. Однак знайшлися й такі, що звинувачували його спрощений підхід до дисципліни. Справді, Безу займався розв’язування алгебраїчних рівнянь, пов’язаних з використанням детермінантів, не зупиняючись на теорії методу.

Хоча він провів важливі дослідження в області алгебраїчних рівнянь, Етьєн Безу пам’ятають, перш за все, за його внесок у математичну освіту. У Франції та за її кордоном до 1848 року був дуже популярний його шеститомний «Курс математики», написаний ним в 1764-1769 роках, якраз тоді, коли працював учителем французьких військових. Викладаючи, Безу був переконаний, що для підготовки артилерійських офіцерів краще відмовитись від теоретичного підходу на користь практичного, і в результаті з’явився дуже зрозумілий підручник. Цей підручник свого часу вплинув на викладання математики по обидві сторони Атлантики.

Безу розвинув метод невизначених множників, у елементарній алгебрі його ім’ям названо спосіб розв’язання систем рівнянь, заснованих на цьому методі та одна з основних теорем алгебри.

Безу помер 27 вересня 1783 року в Бас-Логес, Франції, за шість років до Французької революції, революції соціальних, наукових та інтелектуальних знань країни. Але його вплив поширився далеко в наступні століття.

3.2 Теорема Безу

Теорему Безу: Остача від ділення многочлена Pn(x) на двочлен (x-a) дорівнює значенням цього многочлена при x = a.

Нехай Pn(x) – даний многочлен степеня n, двочлен (x-a) – його дільник, Q_n-1(x) – частка від ділення Pn(x) на x – a (многочлен степеня n-1), R – остача від ділення (R не містить змінної x як дільник першого степеня відносно x).

Доведення:

Відповідно до правила ділення многочленів із остачею можна записати:

Pn(x) = (x – а) Q_n-1(x) + R.    (3.2.1)

Звідси при x = a:

Pn(a) = (a – a)Q_n-1(a) + R = 0 · Q_n-1(a) + R = 0 + R = R.       (3.2.2)

Отже, R = Pn(a), тобто остача від ділення многочлена на (x – a) дорівнює значенню цього многочлена при x = a, що й потрібно було довести.

 

 

3.3 Наслідки з теореми Безу

Наслідок 1: Остача від ділення многочлена Pn(x) на двочлен ax + b дорівнює значенню цього многочлена при x = -b/a, тобто R = Pn(-b/a).

Доведення:

Відповідно до правила ділення многочленів:

Pn(x)= (ax + b) · Q_n-1(x) + R.    (3.3.1)

При x= -b/a:

Pn (-b/a) = (a · (-b/a) + b) · Q_n-1(-b/a) + R = (-b + b)·Q_n-1(-b/a) + R = R.

Отже, R = Pn (-b/a), що й потрібно було довести.

Наслідок 2: Якщо число a є коренем многочлена P(x), то цей многочлен ділиться на (x – a) без остачі:

Доведення:

За теоремою Безу остача від ділення многочлена P(x) на x – a дорівнює P(a), а за умовою a є коренем P(x), а це означає, що P(a) = 0, що й потрібно було довести.

З цього наслідку теореми Безу видно, що задача розв’язування рівняння P(x) = 0 рівносильна задачі виділення дільників многочлена P, маючих перший степінь (лінійні дільники).

Наслідок 3: Якщо многочлен P(x) має попарно різні корені a₁, a₂, … ,a_n, то він ділиться на добуток (x – a₁)…(x – a_n) без остачі. 

Доведення:

Проведемо доведення за допомогою математичної індукції за кількістю коренів. При n=1 твердження доведено у наслідку 2. Нехай воно доведено для випадку, коли кількість коренів дорівнює k, це означає, що P(x) ділиться без остачі на (x – a₁)(x – a₂)…(x – a_k), де a₁, a₂,…,a_k – його корені.

Нехай P(x) має k+1 попарно різних коренів. За припущенням індукції a₁, a₂, a_k … , a_k+1, є коренями многочлена, а, отже, многочлен ділиться на добуток (x – a₁)…(x – a_k), звідки виходить, що Р(x) = (x – a₁)…(x – a_k)Q(x).

При цьому a_k+1 – корінь многочлена P(x), тобто P(a_k+1) = 0. Отже, підставляючи замість x – a_k+1, отримуємо правильну рівність:

P(a_k+1) = (a_k+1 – a₁) … (a_k+1 – a_k)Q(a_k+1) = 0.

Але a_k+1 відмінне від чисел a₁, a₂,…,a_k, і тому жоден з чисел a_k+1 – a₁,      ,…, a_k+1 – a_k не дорівнює 0. Отже, нулю дорівнює Q(a_k+1), тобто a_k+1 – корінь многочлена Q(x). А з наслідку 2 виходить, що Q(x) ділиться на x –    – a_k+1 без остачі.

Q(x) = (x – a_k+1)Q₁(x), і тому P(x) = (x – a₁) … (x – a_k)Q(x) =                     = (x – a₁)…(x – a_k)(x – a_k+1)Q₁(x).

Це означає, що P(x) ділиться на (x – a₁) … (x – a_k+1) без остачі.

Отже, доведено, що теорема правильна при k=1, та з її справедливості при n=k випливає, що правильна і при n=k+1. Отже, теорема правильна незалежно від кількості коренів, що й потрібно було довести.

Наслідок 4: Многочлен степеня n має не більш n різних коренів

Доведення:

Скористаємося методом від супротивного: якщо би многочлен Pn(x) степеня n мав би більш, ніж n коренів – n+k (a₁, a₂,…,a_n+k – його корені), тоді за раніше доведеним наслідком 3 він би ділився на добуток                  (x – a₁)…(x – a_n+k), має степінь n+k, що неможливо. Ми отримали протиріччя, отже наше припущення не вірне і многочлен степеня n не може мати більш, ніж n коренів, що й потрібно було довести.

Наслідок 5: Для будь-якого многочлена P(x) і числа a різниця (P(x) – P(a)) ділиться без остачі на двочлен (x – a).

Доведення:

Нехай P(x) – даний многочлен степеня n, a – будь-яке число. Многочлен Pn(x) можна представити у вигляді:

Pn(x) = (x – a)Q_n-1(x) + R, де Q_n-1(x) – многочлен, частка від ділення Pn(x) на (x – a), R – остача від ділення Pn(x) на (x – a). Причому за теоремою Безу: R = Pn(a), тобто Pn(x) = (x – a)Q_n-1(x) + Pn(a).

Звідси Pn(x) – Pn(a) = (x – a)Q_n-1(x), але це і означає ділення без остачі (Pn(x) – Pn(a)) на (x – a), що й потрібно було довести.

Наслідок 6: Число a є коренем многочлена P(x) степеня не нижче першого тоді і тільки тоді, коли P(x) ділиться на (x – a) без залишку.

Доведення:

Щоб довести цю теорему потрібно розглянути необхідність, і достатність сформульованої умови.

Необхідність: Нехай a – корінь многочлена P(x), тоді з наслідку 2 P(x) ділиться на (x – a) без остачі.

Таким чином, подільність P(x) на (x – a) є необхідною умовою для того, щоб a було коренем P(x), так як є наслідком з цього.

Достатність: Нехай многочлен P(x) ділиться без остачі на (x – a), тоді R = 0, де R – остача від ділення P(x) на (x – a), але за теоремою Безу    R = P(a), звідки виходить, що P(a) = 0, а це означає, що a було коренем P(x).

Отже, подільність P(x) на (x – a) є достатньою умовою того, щоб a є коренем P(x).

Подільність P(x) на (x – a) є необхідною і достатньою умовою для того, щоб a було коренем P(x), що й потрібно було довести.

3.4 Приклади застосування теореми Безу

При розв’язуванні рівнянь за допомогою теореми Безу необхідно:

• знайти всі цілі дільники вільного члена;
• з цих дільників знайти хоча б один корінь рівняння (a);
• ліву частину рівняння розділити на (x – a);
• записати в лівій частині рівняння розклад многочлена на множники;
• вирішити отримані рівняння.

Приклад 1: Знайти остачу від ділення многочлена x³ – 3x² + 6x – 5 на двочлен x – 2.

Розв’яжемо рівняння: x – 2 = 0  =>  x = 2

За теоремою Безу: R = f(2) = 2³ – 3·2² + 6·2 – 5 = 8 – 12 + 12 – 5 = 3.

Відповідь: R = 3.

Приклад 2: Знайти остачу від ділення многочлена 32x⁴ – 64x³ + 8х² + 36x + + 4 на двочлен 2x – 1.

Розв’яжемо рівняння: 2x – 1 = 0 => 2x = 1 => x = ¹/₂

За теоремою Безу: R = f(¹/₂) = 32·(¹/₂)⁴ – 64·(¹/₂)³ + 8·(¹/₂)² + 36·¹/₂ + 4 = 2 –    – 8 + 2 + 18 + 4 = 18.

Відповідь: R = 18.

Приклад 3: При якому значенні a многочлен x⁴ + ax³ + 3x² – 4x – 4 ділиться без остачі на двочлен x – 2?

Розв’яжемо рівняння: x – 2 = 0  => x = 2

За теоремою Безу: R = f(2) = 2⁴ + a·2³ + 3·2² – 4·2 – 4 = 8a + 16. Але за умовою R = 0, значить 8a +16 = 0, звідси a = -2 .

Відповідь: a = -2.

Приклад 4: При яких значеннях a і b многочлен ax³ + bx² – 73x + 102 ділиться на тричлен x² – 5x + 6 без остачі?

Розкладемо дільник на множники: x² – 5x + 6 = (x – 2)(x – 3). Оскільки двочлен x-2 і x-3 взаємно прості, то даний многочлен ділиться на x-2 і на    x-3, а це означає, що за теоремою Безу:

R = f (2) = 8a + 4b – 146 + 102 = 8a + 4b – 44 = 0

R = f (3) = 27a + 9b – 219 + 102 = 27a + 9b – 117 = 0

Вирішимо систему рівнянь:

    

Відповідь: a = 2, b = 7.

Приклад 5: Розв’язати рівняння x⁴ + 3x³ – 13x² – 9x + 30 = 0.

Дільники числа 30: ± 1; ± 2, ± 3, ± 5, ± 6, ± 10, ± 15, ± 30.

R = f (1) = 1⁴ + 3·1³ – 13·1² – 9·1 + 30 = 1 + 3 – 13 – 9 + 30 = 12.

R = f (-1) = (-1)⁴ + 3·(-1)³ – 13·(-1)² – 9·(-1) + 30 = 1 – 3 – 13 + 9 + 30 = 24.

R = f (2) = 2⁴ + 3·2³ – 13·2² – 9·2 + 30 = 16 + 24 – 52 – 18 + 30 = 0.

Даний многочлен ділиться на x-2 без остачі:

_ х⁴ + 3x³ – 13x² – 9x + 30 x – 2

   x⁴ – 2x³    x³ + 5x² – 3x – 15

       _  5х³ – 13x²

          5x³ – 10x²

               _ -3x² – 9x

                  -3х² + 6x

                         _ -15x + 30

                            -15х + 30

                                         0

(х – 2) (x³ + 5x² – 3x – 15) = (х – 2)(x + 5)(x² – 3) = 0.

Відповідь: x₁ = 2, x₂ = -5, x_3,4 = ±√3.

Приклад 6:  Розв’язати рівняння x⁶ + x⁵ – 7x⁴ – 5x³ + 16x² + 6x – 12 = 0.

Дільники числа 12: ± 1; ± 2, ± 3, ± 4, ± 6, ± 12.

За теоремою Безу:

R = f (1) = 1⁶ + 1⁵ – 7∙1⁴ – 5∙1³ + 16∙1² + 6∙1 – 12 = 0.

_ x⁶ + x⁵ – 7x⁴ – 5x³ + 16x² + 6x – 12    x – 1

  x⁶ – x⁵                                                    x⁵ + 2x⁴ – 5x³ – 10x² + 6x + 12

       _2х⁵ – 7x⁴

        2 x⁵ – 2x⁴

               _– 5x⁴ – 5x³

                 – 5х⁴ + 5x³

                          _ – 10x³ + 16x²

                             – 10х³ + 10x²

                                          _ 6x² + 6x

                                             6x² – 6x

                                                   _ 12x – 12

                                                      12x – 12

                                                                 0

x⁶ + x⁵ – 7x⁴ – 5x³ + 16x² + 6x – 12 = (x – 1)(x⁵ + 2x⁴ – 5x³ – 10x² + 6x + 12) = = 0

x⁵ + 2x⁴ – 5x³ – 10x² + 6x + 12 = 0

Дільники числа 12: ± 1; ± 2, ± 3, ± 4, ± 6, ± 12.

За теоремою Безу:

R = f (1) = 1 + 2 – 5 – 10 + 6 + 12 = 6.

R = f (-1) = -1 + 2 + 5 – 10 – 6 + 12 = 2.

R = f (2) = 32 + 32 – 40 – 40 + 12 + 12 = 8.

R = f (-2) = -32 + 32 + 40 – 40 – 12 + 12 = 0.

_ x⁵ + 2x⁴ – 5x³ – 10x² + 6x + 12   х + 2

  x⁵ + 2x⁴                                                x⁴ – 5x² + 6

               _ 5x³ – 10x²

                  -5х³ – 10x²

                                      _ 6x + 12

                                         6x + 12

                                                   0

x⁶ + x⁵ – 7x⁴ – 5x³ + 16x² + 6x – 12 = (x – 1)(х + 2)(x⁴ – 5x² + 6) = 0

x⁴ – 5x² + 6 = 0 – біквадратне рівняння, x_1,2 = ±√3, х_3,4 = ±√2.

Відповідь: x_1,2 = ±√3, х_3,4 = ±√2, х₅ = 1, x₆ = -2.

Приклад 7. Розв’язати рівняння x³ – 5x² + 8x – 6 = 0.

Дільники числа 6: ± 1; ± 2, ± 3, ± 6.

За теоремою Безу:

R = f (1) = 1 – 5 + 8 – 6 = -2.

R = f (-1) = -1 – 5 – 8 – 6 = -20.

R = f (2) = 8 – 20 + 16 – 6 = -2.

R = f (-2) = -8 – 20 – 16 – 6 = -50.

R = f (3) = 27 – 45 + 24 – 6 = 0.

_ x³ – 5x² + 8x – 6    x – 3

   x³ – 3x²                  x² – 2x + 2

       _ -2x² + 8x

          -2x² + 6x

                  _ 2x – 6

                     2x – 6

                            0

x³ – 5x² + 8x – 6 = (x – 3) (x² – 2x + 2) = 0

x² – 2x + 2 = 0 – квадратне рівняння, дійсних коренів немає, так як D < 0.

Відповідь: x = 3.

Приклад 8. Розв’язати рівняння 6x³ + 11x² – 3x – 2 = 0.

Дільники числа 2: ± 1; ± 2.

За теоремою Безу:

R = f (1) = 6 + 11 – 3 – 2 = 12.

R = f (-1) = -6 + 11 + 3 – 2 = 6.

R = f (2) = 48 + 44 – 6 – 2 = 84.

R = f (-2) = -48 + 44 + 6 – 2 = 0.

_6x³ + 11x² – 3x – 2   x + 2

  6x³ + 12x²                 6x² – x – 1

           _  -x² – 3x

               -x² – 2x

                    _ -x – 2

                       -x – 2

                              0

6x³ + 11x² – 3x – 2 = (6x² – x – 1) (x +2) = 0

6x² – x – 1 = 0 – квадратне рівняння, x₁ = ½, x₂ = -⅓.

Відповідь: x₁ = ½, x₂ = -⅓, x₃ = -2.

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВОК

Працюючи над темою «Теорема Безу та її наслідки», ми переконались, що вона надзвичайно важлива і актуальна з усіх розділів математики.

Теорема Безу – одна з основних теорем алгебри, названа ім'ям французького вченого Етьєна Безу.

Існує кілька наслідків з теореми, які допомагають при розв’язуванні практичних завдань. З розглянутих прикладів можна зробити висновок, що теорема Безу знаходить застосування при вирішенні завдань, пов'язаних з подільністю многочленів, наприклад, знаходження остачі при діленні многочленів, розкладання многочленів на множники, визначення кратності коренів тощо.

Запропонована робота дозволяє повторити всі основні прийоми розв’язування рівнянь (квадратних, третього степеня і вище), пов'язані із застосуванням теореми Безу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Істер О.С. Алгебра: підруч. для 8-го кл. загальноосвіт. Навч. Закл./О.С. Істер. – Київ: Генеза, 2016. – 272 с.
2. Мерзляк А.Г. Алгебра: підруч. для 8 кл. з поглибленим вивченням математики./А.Г. Мерзляк, В.Б. Полонський, М.С. Якір О.С. – Х: Гімназія, 2016. – 384 с.
3. Мерзляк А.Г., Полонський В.Б., Рябінович Ю.М., Якір М.С. Збірник задач і контрольних робіт з алгебри для 8 класу. – Х.: Гімназія, 2016. – 96 с.
4. Кучевський М. І., Квадратні рівняння. // Математика в школах України. – 2007. –  С. 34-38.
5. Математична енциклопедія, т. 2, під ред. І.М. Виноградова. – М: Радянська енциклопедія, 1979.
6. Перельман,  Я.І. Цікава алгебра. / Я. І. Перельман – М.: Наука, 1976 р.
7. wikipedia.org/wiki …