Урок №1. "Функция у=х^2 и ее график."

Алгебра. 8 класс.

Урок № 1           § 11

Тема:  Функция и ее график.

Цель урока:

Образовательная:  рассмотреть функцию и ее свойства, уметь строить график функции, решать уравнения с использованием графика функции  .

 Развивающая:  развитие вычислительных и графических навыков.

Воспитательная: воспитание прилежности, аккуратности . 

Тип урока: урок усвоения новых знаний и умений

Оборудование: мел, доска, учебник, линейка.

 

Х о д   у р о к а

 

1. Организационный момент.

 

Добрый день! Добрый час!

Как я рада видеть вас.

Прозвенел уже звонок

Начинается урок.

Улыбнулись. Подровнялись.

Друг на друга поглядели

И тихонько дружно сели.

 

2. Мотивация урока.

 

Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя.

Анализ контрольной работы

 

3. Объяснение нового материала

 

 Рассмотрим функцию, заданную формулой у = х². Область её опреде­ления - множество всех чисел.

 Составим таблицу значений функции для некоторых зна­чений аргумента х:

 

 

х	-3	-2,5	-2	-1,5	-1	0	1	1,5	2	2,5	3
у	9	6,25	4	2,25	1	0	1	2,25	4	6,25	9

 

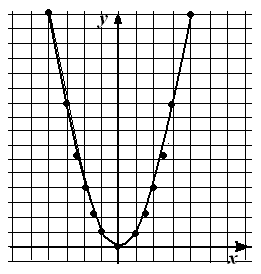
 Нанесём точки, координаты которых приведены в этой таблице.

 

 

            

 

 

 

 

 

 

 

 

 

                -3 -2 -1  0   1  2       4                                        -3 -2 -1  0   1  2       4                                         

 

 

 

   Если на координатной плоскости нане­сти больше точек с координатами  х и у, удовлетворяющих формулу  у = х², то они разместились бы так, как показано на  втором рисунке. Если для каждого действительного значе­ния  х  по формуле     у = х² вычислить соответствующее значе­ние  у  и обозначить точки с такими координатами на коорди­натной плоскости, то получим непрерывную кривую линию, которую называют параболой. Парабола имеет две бесконечных ветви, плавно сходящиеся в одной точке — вершине параболы.

Для функции  у = х² вершиной параболы является точ­ка (0; 0). То есть график функции  у = х²  проходит через начало координат. Поскольку противоположным значениям ар­гумента соответствуют равные значения функции, то её гра­фик симметричен относительно оси у. Построенный график даёт возможность наглядно выра­зить свойства функции   у = х².

  Рассматривая график мы можем сказать, что функция у = х² обладает такими свойствами:

Область определения –               любое  число.

Область значения –                 все неотрицательные числа (у  ≥  0)

Промежутки убывания –           когда  х < 0

Промежутки возрастания –     когда  х > 0

Нули функции (значение аргумента, при котором значение функции равно 0)         –              х=0 

  Для чего надо знать, каков график функции? Подробнее об этом вы узнаете в старших классах. А сейчас обратите внимание на то, что с помощью графиков функций можно решать уравнения, которые иными способами решить слож­но либо невозможно.

  Сколько решений имеет уравнение х² = 9? Прямая (её урав­нение у = 9) пересекает график функции у = х² в двух точках (рис. 3).

 

 

 

 

 

 

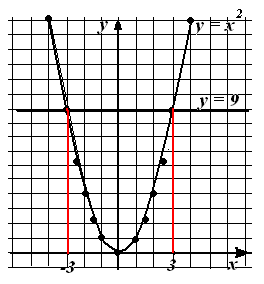
           х² = 9 

         х  = 3  или  х  = - 3

 

 

 

 

 

 

 

 

 

 

  Их абсциссы х = 3 и х = - 3 — решения уравнения.

  Так же можно решить более сложное уравнение  х² – 3х – 4 = 0.

  Сначала представим это уравнение в виде  х² =  3х + 4.

 

 

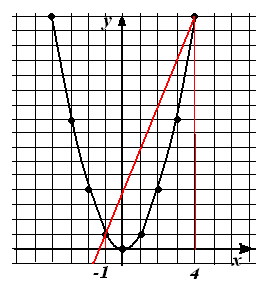
Графики функций

у = х²   и  у = 3х + 4.

пересекаются в точках с

абсциссами  х = -1 и х = 4,

которые в свою очередь являются

решениями  данного уравнения. 

 

 

 

 

 

 

4. Закрепление изученного материала.

    Опираясь на график функции у = х² , весь класс отвечает на вопросы задания № 350.

  Вопрос классу. Как можно определить проходит ли график функции через ту или иную точку?

  После выполнения задания  рассматриваем свойства функции у = - х²

5. Физкультурная пауза.
Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе.
1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3—4 раза.
3. Медленно наклоняйте голову: вперед—влево— вправо -  назад. Повторите 3-4 раза.
4. Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.

 

6. Проблемная ситуация:

  Сколько решений имеет уравнение х² =5, и как их найти? Попробуем ответить на этот вопрос самостоятельно, учащиеся приходят к мысли, что корни они могут найти приближенно.

 

7. Итоги урока. Рефлексия.

  Что мы узнали нового?

 Как называется график функции у = х² ?

 Какими свойствами она обладает?

 

8.  Домашнее задание  § 11,  № 351, 352, на повторение №368