ЛЬВІВСЬКА МІСЬКА РАДА

Департамент гуманітарної політики управління освіти

Відділ освіти Сихівського району

Середня загальноосвітня школа № 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Чого немає у підручниках математики

(розвиток логічного мислення засобами математики)

 

 

 

 

 

 

 

 

ЛЕВ  АЛЛА  ЯРОСЛАВІВНА

вчитель математики

вищої кваліфікаційної категорії,
методист

 

 

 

 

 

 

 

 

 

 

ЛЬВІВ 2017 р.

Анотація

Розвиток у дітей логічного мислення – це одна з важливих задач навчання. Уміння мислити логічно, виконувати умовиводи без наочної опори, зіставляти судження за визначеними правилами – необхідна умова успішного засвоєння навчального матеріалу. В будь-якій задачі закладені великі можливості для розвитку логічного мислення. Нестандартні логічні задачі – відмінний інструмент для такого розвитку. Використання на уроках математики і позаурочних заняттях спеціальних задач і завдань, спрямованих на розвиток логічного мислення, розширює математичний кругозір і дозволяє більш впевнено орієнтуватися в найпростіших закономірностях навколишньої  дійсності й активніше використовувати математичні знання в повсякденному житті.

"Головна задача навчання математиці, причому із самого початку, з першого класу, - учити міркувати, учити мислити", - писав педагог-новатор А.А. Столяр.

Найважливішою задачею математичної освіти є озброєння учнів загальними прийомами мислення, просторової уяви, розвиток здатності розуміти зміст поставленої задачі, уміння логічно міркувати, засвоїти навички алгоритмічного мислення.  Кожному важливо навчитися аналізувати, відрізняти гіпотезу від факту, чітко виражати свої думки, а з іншого боку - розвити уяву й інтуїцію (просторове представлення, здатність передбачати результат і угадати шлях рішення). Саме математика надає сприятливі можливості для виховання волі, працьовитості, наполегливості в подоланні труднощів, завзятості в досягненні цілей.

Зміст

1. Математика для всіх

2. Інтегрований урок з математики та історії «Прості і складені числа» (6 клас)

3. Інтегрований урок з математики і географії «Декарт і його координати» (6 клас)

4. Урок-гра «Веселі дроби» (5 клас)

6. Інтегрований урок з математики і мистецтва «Відношення і пропорції»

7. Вечір математики «Спочатку було слово»

8. Позакласний захід з математики «І жартома і всерйоз»

9. Гра «Я знаю, що нічого не знаю».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МАТЕМАТИКА ДЛЯ ВСІХ

  "Математика для всіх"  - це принцип розвиваючої функції навчання математиці. Відповідно до цього принципу центром системи навчання математиці стає не вивчення основ математичної науки як такий, а пізнання навколишнього світу засобами математики і, як наслідок, адаптація людини до цього світу, до соціалізації особистості.

 Основною метою математичної освіти повинне бути розвиток уміння математично, тобто логічно й усвідомлено, досліджувати явища реального світу. Реалізації цієї мети сприяє розв’язування на уроках математики і в позаурочний час різного роду нестандартних логічних задач. Тому використання вчителем школи цих задач є не тільки бажаним, але навіть необхідним елементом навчання математиці.

Більшість учнів, навіть старшокласників, не опановує початковими прийомами логічного мислення (аналіз, порівняння, синтез, абстрагування й ін.). Роль математики в розвитку логічного мислення винятково велика. Причина настільки виняткової ролі математики в тому, що це найбільш теоретична наука з усіх досліджуваних у школі.

У ній високий рівень абстракції і у ній найбільш природним способом викладу знань є спосіб переходу від абстрактного до конкретного. У шкільному віці одним з ефективних способів розвитку мислення є розв’язування  школярами нестандартних логічних задач, які здатні прищепити інтерес дитини до вивчення «класичної» математики.

У цьому відношенні дуже характерний наступний приклад. Найбільший математик сучасності, творець московської математичної школи, академік Микола Миколайович Лузін, будучи гімназистом, одержував по математиці суцільні двійки. Учитель прямо сказав батькам Н.Н. Лузіна, що їхній син у математиці безнадійний, що він тупий і що навряд чи він зможе учитися в гімназії. Батьки найняли репетитора, за допомогою якого хлопчик ледь-ледь перейшов у наступний клас. Однак репетитор цей виявився людиною розумною і проникливою. Він помітив неймовірну річ: хлопчик не умів вирішувати прості, примітивні задачі, але в нього іноді раптом виходили задачі нестандартні, набагато більш складні і важкі. Він скористався цим і зумів зацікавити математикою цього, здавалося б, бездарного хлопчика. Завдяки такому творчому підходу педагога з хлопчика згодом вийшов учений зі світовим ім'ям, який не тільки багато зробив для математики, але і створивший найбільшу радянську математичну школу.

Розвиток у дітей логічного мислення – це одна з важливих задач навчання. Уміння мислити логічно, виконувати умовиводи без наочної опори, зіставляти судження за визначеними правилами – необхідна умова успішного засвоєння навчального матеріалу. В будь-якій задачі закладені великі можливості для розвитку логічного мислення. Нестандартні логічні задачі – відмінний інструмент для такого розвитку. Використання на уроках математики і позаурочних заняттях спеціальних задач і завдань, спрямованих на розвиток логічного мислення, розширює математичний кругозір і дозволяє більш впевнено орієнтуватися в найпростіших закономірностях навколишньої  дійсності й активніше використовувати математичні знання в повсякденному житті.

"Головна задача навчання математиці, причому із самого початку, з першого класу, - учити міркувати, учити мислити", - писав педагог-новатор А.А. Столяр.

Найважливішою задачею математичної освіти є озброєння учнів загальними прийомами мислення, просторової уяви, розвиток здатності розуміти зміст поставленої задачі, уміння логічно міркувати, засвоїти навички алгоритмічного мислення.  Кожному важливо навчитися аналізувати, відрізняти гіпотезу від факту, чітко виражати свої думки, а з іншого боку - розвити уяву й інтуїцію (просторове представлення, здатність передбачати результат і угадати шлях рішення). Саме математика надає сприятливі можливості для виховання волі, працьовитості, наполегливості в подоланні труднощів, завзятості в досягненні цілей.

Сьогодні математика як жива наука з багатобічними зв'язками, що робить істотний вплив на розвиток інших наук і практики, є базою науково-технічного прогресу і важливим компонентом розвитку особистості. Однієї з основних цілей вивчення математики є формування і розвиток мислення людини, насамперед, абстрактного мислення, здатності до абстрагування й уміння "працювати" з абстрактними, "невловимими" об'єктами. У процесі вивчення математики в найбільш чистому виді може бути сформоване логічне (дедуктивне) мислення, алгоритмічне мислення, багато якостей мислення - такі, як сила і гнучкість, конструктивність і критичність і т.д.

      Позакласна робота з математики – це заняття, які проводяться в позаурочний час, ґрунтуються на принципі добровільної участі, мають на меті підвищення рівня математичного розвитку учнів і цікавості до предмета за рахунок поглиблення і розширення базового змісту програми. Позакласні заняття можна будувати як на матеріалі, лише посередньо пов'язаному зі шкільною програмою, так і на матеріалі, який безпосередньо межує з темами обов'язкової програми, але не дублює цю роботу, а поглиблює і дещо розширює її. Між навчально-виховною роботою, що проводиться на уроках, і позакласною роботою існує тісний взаємозв'язок: навчальні заняття, розвиваючи у учнів інтерес до знань, сприяють розвертанню позакласної роботи, і навпаки, позакласні заняття, що дозволяють учням застосовувати знання на практиці, розширюють і поглиблюють ці знання, підвищують успішність учнів та їх інтерес до навчання. Але позакласна робота не повинна дублювати навчальну роботу, інакше вона перетвориться в звичайні додаткові заняття.

 

 

 

 

 

 

 

 

 

 

 

 

 

Інтегрований урок  з математики  та історії

«Прості і складені числа»

6 клас

Актуалізація опорних знань

Нам приємно, коли до нас приходять гості. Ми їм щиро радіємо, садимо на найпочеснішому місці, намагаємось зацікавити, щоб їм у нас було весело і цікаво. «Гість у дім – радість в нім» - так говорить народна мудрість. Це все приказка, а казка у нас попереду. Отож, починаємо. Жили-були числа. Виникли вони з потреб людини. За допомогою них людина стала рахувати все, що її оточує. Додавала і віднімала, множила і ділила. Числа були сірі, сухі, звичайні, нічим особливим не вирізнялись. Просто виконували свою роботу. І от одного разу числа ожили і заговорили. Надоїло їм бути однаковими і почали вони шукати свої особливості. Виявилось, що не такі вони вже й однакові, не такі вони вже й сірі. Точно так, як у нас, у людей. Зараз ми сидимо на уроці всі ніби однакові учні 6 класу, а після уроків кожен з вас зможе показати чим він відрізняється від інших: одні малюють, інші грають, танцюють, співають. А ще є у нас спортсмени, математики, юні поети. Кожен з вас вже є маленька особистість, зі своїми особливостями, здібностями, нахилами.

Та повернемось до натуральних чисел. Що нам уже про них відомо? Давайте пригадаємо:

1. Які числа називаються натуральними?
2. Що таке натуральний ряд чисел?
3. Назвіть найменше і найбільше натуральне число.
4. На які числа поділяються натуральні за подільністю?
5. Коли кажуть, що число b є дільником числа a?
6. Сформулюйте означення простого числа.
7. Назвіть 5 перших простих чисел.
8. Назвіть 5 перших складених чисел.
9. Чому число 7 просте, а 6 складене? Скільки є простих чисел, а скільки складених?
10. Яке з простих чисел є парним?
11. Які з простих чисел є сусідніми в натуральному ряді.
12. Як ви думаєте, чому немає більше простих чисел-сусідів?
13. А що це за числа-близнята?
14. Знайдіть на форзаці підручника в таблиці простих чисел пари чисел-близнят в останній сотні; в першій сотні.

 

Ну от і добре, це ви вже знаєте. А про інші особливості натуральних чисел ми будемо вивчати на наступних уроках. Як бачите скільки цікавого можна помітити в числах, якщо уважно до них придивлятись і вивчати. Та повернемось до нашої казки.

   Число 28 вирішило запросити до себе в гості своїх менших дільників. Допоможіть назвати хто прийшов у гості до числа 28. Вірно, це 1;2;4;7;14.

Коли всі зібралися, число 28 помітило, що їх небагато. Засумувало і запропонувало, щоб кожен з гостей запросив своїх дільників. Та виявилось. Що нових гостей не буде. Одиниця пояснила (а вона головна, бо з неї все починається), що така особливість дільників усіх чисел.

 ( Дома перевірити для числа 30).

  Щоб заспокоїти число 28 гості з’єдналися  знаком «+». І, о чудо, сума виявилась рівною 28. Одиниця пояснила (а вона головна в нас, як ви вже знаєте), що число, сума дільників якого дорівнює йому самому, називається досконалим. Число 28 поцікавилось, що означає - «досконале». Тоді Одиниця запропонувала звернутись до тлумачного словника. Числа прочитали (читаємо у «Великому тлумачному словнику сучасної української мови»):

«Досконалий – який має потрійний ступінь довершеності, який визначається повнотою позитивних якостей, довершений, повний, абсолютний.»

Число 28 загордилось. Ось яке я, неперевершене. Та Одиниця сказала, що досконалі числа ще є, хоч і зустрічаються дуже рідко. Серед трицифрових чисел є тільки одне, 496 і тільки одне одноцифрове. Що число 496 досконале перевіримо на наступному уроці, коли вивчимо тему, як знайти всі дільники багатоцифрового числа. Одноцифрове досконале пропоную знайти зараз. Вірно, це число 6 =1+2+3.

Число 28 запросило до себе в гості і число 6. Стали поряд. Щоб сфотографуватись. Між ними непомітно втиснулись Нуль і всюдисуща Точка, щоб потрапити в кадр з такими знаменитостями. На фотознімку виявилось ось що  «28.06». Всі помітили, що це схоже на якусь дату. А хто з вас прочитає цю дату і пригадає, що з нею пов’язано?

Так, це 28 червня День Конституції України – Основного Закону нашої держави.

Конституція України прийнята на 5 сесії Верховної Ради України 28 Червня 1996 року. З цим Законом і окремими його положеннями ви будете знайомитись на уроках історії, правознавства. Прочитаємо лише дві статті з цього закону:

Стаття 52. Діти рівні у своїх правах незалежно від походження.

Стаття 53. Кожен має право на освіту.

Та повернемось до чисел. Стали вони вітати дві такі знаменитості, дві такі досконалості серед них. Принесли квіти. Кожне число стільки квіток, скільки воно значить: 1; 2; 4; 7; 14. У букеті, який дарують на свято, повинно бути непарне число квіток. Як можна скласти два букети з цих квітів? Об’єднайте числа між собою, які можуть утворити такі букети .

 Числам сподобалось ходити в гості. Стали вони запрошувати свої дільників.

Завдання. Виясніть скільки гостей-дільників прийде до чисел 17, 15, 14.

   Тільки одне число не дочекалось гостей. Яке? Так , це 1.

   А скільки разів воно побувало в гостях?

   У яких чисел був лише 1 гість?

Ось і казці кінець, а хто слухав і працював – молодець!

Про які особливі числа ми сьогодні дізналися?

Чим же вони особливі?

Чи багато їх?

Як бачимо. Числа не такі вже й безликі, сірі та скучні. Серед них як ви вже помітили, є прості і складені, парні і непарні, числа-сусіди, числа-близнята, досконалі числа. Ще багато нових відкриттів нас чекає попереду. Удосконалюймо свої знання в математиці. У досконалості немає меж.

 

Інтегрований  урок з математики і географії

в 6 класі

“Декарт і його координати”

У математичних пошуках є дуже вдалі

винаходи, здатні принести велику користь,

 задовольняють любов до знань, полегшують

 ремесла і скорочують працю людини.

Рене Декарт

Мета уроку: Систематизувати відомості про координати на площині. Розвивати логічне мислення, уяву. Формувати знання про зв’язок математики з іншими предметами, науками (географією, інформатикою, мореплавством, військовою справою). Виховувати інтерес до праці, до здобування знань.

Обладнання: Прикладна комп’ютерна програма “Gran 1”, карта світу,  модель координатної площини, картки з завданнями, портрет Р.Декарта.

 

ХІД   УРОКУ

 

I. Актуалізація опорних знань.

 Історична довідка. Два учні зачитують коротку інформацію про систему координат на площині.

1-й учень (Математик) Французький математик Оресм у XIV ст. ввів за аналогією до географічних координат координати на площині. Таке нововведення було надзвичайно прогресивним. На його основі виник метод координат, який пов’язав алгебру з геометрією. Геометричне поняття “точка” пов’язане з алгебраїчним поняттям “пара чисел”.

Основна заслуга у введенні координат належить французькому математику Рене Декарту. Тому систему координат називають декартовою. Її ще називають прямокутною, оскільки осі перетинаються під прямим кутом. Осі мають назви : горизонтальна – вісь абсцис, вертикальна – вісь ординат. Щоб знайти координати точки, тобто її місце знаходження на площині – необхідно з даної точки провести перпендикулярні прямі до осей координат і знайти відповідні числові значення спочатку на осі абсцис, потім на осі ординат.

2-й учень (географ) На глобусі і карті роль осей координат замінюють: нульовий або Гринвіцький меридіан - вісь ординат, екватор - вісь абсцис. Східна довгота відповідає додатній частині осі абсцис, західна довгота – від’ємній частині; північна широта відповідає додатній частині осі ординат, південна широта – від’ємній  частині. Координати об’єкту  на карті записуються в градусах з позначкою в якій частині півкулі він знаходиться. Наприклад м. Київ має такі координати.

 Учитель. А як це вміють робити учні на площині і на карті ми зараз побачимо. Домовимось про таку умовність: 10 градусів на карті відповідають 1 одиничному відрізку на координатній площині. До дошки викликаються два учні, які вважають себе кращим географом і кращим математиком класу. Влаштуємо маленький турнір. Один учень показує на карті точку за даними координатами, інший учень показує відповідну їй точку на площині. І навпаки один учень показує точку за її координатами на площині, а інший їй відповідну на карті.

Завдання для географа: 10Пн.ш.30Зх. д.

                                         50Пн.ш.40Сх. д.

Завдання для математика (-5; 4); (-2;-4)

Кожен з учнів називає відповідно в якій частині кулі знаходиться точка чи в якій чверті знаходиться точка.

Учитель. Покажіть на карті м. Львів і назвіть їх координати. Округліть число до десятків і покажіть на координатній площині цю точку.

II.  Практична частина

Учитель. А де ще використовується метод координат?

3-й учень(ерудит). В театральних залах, кінозалах місця для глядачів розміщені у формі першої чверті системи координат. Роль осі абсцис відіграють ряди, а осі ординат місця в рядах. Гра в шахи проходить на дошці в клітку, в якої ряди горизонтальні позначені буквами (вісь абсцис), вертикальні – числами (вісь ординат). Гра  “Морський бій”  також проходить на розлінованому листку схожому на систему координат.

Учитель. В усіх випадках ми маємо справу з визначенням місця знаходження об’єкта на площині. Його задають двома орієнтирами. В кожному разі слід вміти знаходити координати точок, або точки за координатами. В наш час - вік техніки, комп’ютеризації, коли людина підкорює космос, водні простори нашої землі, її надра, вона не може обійтися без  знань математики, інформатики. Ці предмети ми вивчаємо з вами в школі. А от чи відомо вам ще, де крім “Морського бою” чи шахів, використати метод координат?  Комп’ютер тримає в своїй пам’яті великий обсяг різноманітної інформації. Та за допомогою нього можна визначити місце знаходження космічного корабля, бойової ракети, літака в небі, корабля на морі чи в океані. Для цього екран дисплея розбитий на квадрати, довжина сторони якого відповідає сотням, тисячам кілометрів. В цій сітці є дві взаємно перпендикулярні осі. Щоб визначити місце знаходження об’єкта розглядають його як точку на площині, і визначають її координати.

Ми сьогодні побуваємо з вами в ролі диспетчера на аеродромі і прослідкуємо маршрут літака за його координатами. Розділяємось на дві групи. Перша група біля комп’ютера визначатиме маршрут літака за координатами точок, де літак змінював маршрут, а друга група визначатиме за “картою польоту” координати пунктів, в яких літак змінював напрям маршруту. Учням видаються відповідні картки. Потім групи міняються місцями і відповідно змінюються завдання.

Картки-завдання № 1( для комп’ютера) .

Учні знаходять точки на системі координат в програмі „Gran 1” в режимі „Ламана лінія”.

В результаті отримується малюнок, за яким вчитель може зразу дізнатись вірність виконання завдання.

 

1 (0;0)  (-1;1)  (-3;1)  (-2;3)  (-3;3)  (-4;6)  (0;8)  (2;5) (2;11)  (6;10)  (3;9)  (4;5)  (3;0)  (-2;0)  (1;-7)  (3;-8)  (0;-8)  (0;0)

2 (4;7)  (5;8)  (6;8)  (8;9)  (9;9)  (7;8)  (9;8)  (6;7)  (7;6)  (9;6)  (11;5)  (12;3)  (12;2)  (13;3)  (12;1)  (7;1)  (9;2)  (8;3)  (6;1)  (5;1)  (6;2)  (6;3)  (5;6)  (4;6)  (4;7)

Картки-завдання №2

 для визначення координат за готовим малюнком

 

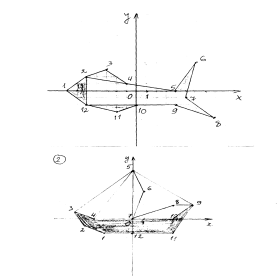
III Контролююча  частина.

Оцінити ваші знання з теми “Координатна площина” допоможе нам комп’ютер за допомогою програмованого тестування.

Тест

1. Раціональні числа – це ...

- цілі, дробові і нуль;

- натуральні числа;

- додатні і від’ємні.

2. Протилежні числа – це числа, які...

- відрізняються знаком;

- знаходяться на одній відстані від нуля;

- мають різні модулі.

3 Додатні числа – це..

- невід’ємні числа;

- числа більші від нуля;

- числа розміщені правіше.

3. Недодатні числа – це..

- числа менші за додатні;

- числа лівіші від нуля;

- числа не більші за нуль.

4. Модуль числа є ...

- число більше за нуль;

- число рівне даному;

- число невід’ємне.

5. Модуль додатного числа є число...

- невід’ємне;

- ціле;

- йому протилежне.

6. Вісь абсцис – це ...

- вертикальна пряма;

- перпендикулярна пряма;

- горизонтальна пряма.

7. Вісь ординат – це...

- вісь Оу;

- вісь Ох;

- вісь ХУ.

8. Якщо точка знаходиться в ІІ чверті, то...

- її координати додатні;

- її абсциса додатна;

- її ординати додатна.

9. Якщо точка знаходиться на осі абсцис, то...

- її ордината рівна нулю;

- її абсциса рівна нулю;

- її координати рівні нулю.

10. Назвати цілі числа, модуль яких менший за 4.

• -4,-3,-2,-1,0,1,2,3,4;
• -3,-2,-1,0,1,2,3;
• 0,1,2,3.

11.Назвати цілі числа, що розміщені між –2,5 і 3,1.

• -2,-1,0,1,2,3;
• -3,-2,-1,0,1,2;
• -2,-1,1,2,3.

В цей час, як частина учнів виконує тестування на комп’ютері, інша частина виконує самостійну роботу в зошитах.

1.Розмістити в порядку спадання числа:

-3,2; 9,4; 0,6; -7,8; -18,6; 0; 19.

2.Записати цілі розв’язки нерівності:

-5 у 6,7.

3. Обчислити :

-14,6 - - 6,8

-6,3:-7.

Розв’язати  рівняння:

х = 6,7;

х+3=7.

В кінці уроку зібрати зошити.

Оцінювання учнів висвітлюється на наступному уроці за результатами всіх видів робіт на уроці.

IV. Підсумок уроку

 

 

 

 

 

Урок-гра  з математики в 5 класі

“Веселі дроби”

Тема: “Дробові числа”

Мета: Закріпити основні вміння і навички читання і запису дробових чисел, порівняння дробів, перетворення в мішане число, додавання і віднімання дробових чисел, знаходження дробу від числа. Формувати вміння застосовувати знання в нестандартних ситуаціях. Прищеплювати інтерес до математики, розвивати кмітливість, спостережливість.

Обладнання: казкові герої Кмітливчик і Заморочок, кодоскоп.

Тип уроку: урок формування вмінь та навичок.

 

ХІД УРОКУ

 

I Актуалізація опорних знань.

До нас на урок завітали два веселих герої Кмітливчик і Заморочок. Вони хочуть погратися з вами. Тому підготували ряд завдань, які ви повинні виконати. Але будьте уважні, бо завдання в них з «заморочками» і хитринками. Покажемо їм, що ми знаємо все, що вивчили про дроби. На початку підготуємось до гри, пригадаємо все, що вивчили.

Правила на уроці. Відповідаємо швидко, чітко, не перебиваємо відповідь товариша, поважаємо один одного. Не засмічуємо мову непотрібними словами. Використовуємо математичну термінологію.

1. Як виникли дробові числа?
2. Чому вони так називаються?
3. Як записуються дробові числа?
4. Що показує чисельник та знаменник дробу?
5. Які дроби називаються правильними, які неправильними? Чому?
6. Як порівнювати дроби?
7. Як додати чи відняти дробові числа?
8. Як перетворити неправильний дріб в мішане число?

     9.Як знайти дріб від числа?

10.Як знайти число за дробом?

II Розв’язування задач (умови частини задач демонструються на кодоскопі, частина сприймається на слух).

Задачки Кмітливчика ідуть з позначкою К, а Заморочка – з позначкою З.

К  Запишіть дріб:

Чотири тисяча других; чотири тисячі других; Чисельник 23, а знаменник на 21 більший; знаменник 42, чисельник на 18 менший; Чисельник 5, знаменник у 12 разів більший; знаменник 72, чисельник у 36 разів менший.

З     Мій зріст км, а маса тони. Ось який я малесенький, спробуйте мене знайти. (Виразити масу і зріст у звичних вимірах).

 К   Знайти дріб, який рівний своєму чисельнику.

       Знайти дріб, який рівний своєму чисельнику.

З   Мені вже надоїло вчитися, тому хочу зробити собі перерву на   доби і з’їсти морозива  ц. Чи не надто багато він хоче? ( Перетворити в звичні міри).

К   Мені видала мама гроші для покупок. Я їх витратив так:   витратив на хліб, – на молоко, – на овочі, – на фрукти. Поміркуйте, на що я витрати грошей найбільше, на що найменше, і чи вистачить мені грошей ще і на морозиво та цукерки для всієї сім’ї?

З  А я хочу з вами погратися. Навіть приз переможцю приготував. Його отримає той хто назве дріб найменший. (Приз отримає учень, який здогадається, що найменшого дробу не існує)

К  Миколка пішов до магазину за покупками. Чи вистачить у нього грошей, якщо на хліб він витратить   всіх грошей, на молоко – , на овочі , на фрукти ? На які продукти він витратить найбільше, а на які найменше?

З Заморочок відправився на гастролі 8 і тижня він провів в Києві, а 3 і тижня в Харкові. Скільки всього тижнів гастролював Заморочко і скільки днів?

К Василько, Петрик, Миколка і Юрчик вирішили погойдатись на гойдалці. Перевірити в кожному випадку хто кого переважить, якщо відомо, що маса Юрчика становить маси Василька, маса Петрика становить маси Василька, маса Миколки становить маси Василька? Випадки можуть бути такі:

Юрчик з Васильком, а Миколка з Петриком;

Юрчик з Миколкою, а Петрик з Васильком;

Юрчик з Петриком, а Миколка з Васильком..

От і закінчився наш урок веселих дробів.  Чи сподобались вам завдання наших друзів Заморочка і Кмітливчика? Надіюсь вони не стомили вас і показали, що не такі вже і страшні ці дроби, якщо з ними дружити.

Домашнє завдання. А додому вам буде завдання скласти казкові, веселі задачі для Заморочка і Кмітливчика з дробами.

 

 

 

 

Узагальнюючий урок з теми

«Відношення і пропорції»

 в 6 класі

Тема:     Узагальнюючий урок з теми “Відношення і пропорції.”.

Мета:    Повторити означення відношення, пропорції; основну властивість пропорції, поняття прямої і оберненої пропорційності. Формувати навички знаходження невідомого члена пропорції, уміння використовувати пропорційність при розв’язуванні текстових задач. Розвивати навички усної лічби, культуру математичного мовлення, бажання пізнавати нове. Прищеплювати інтерес до математики, показати можливості застосовування математика у різних галузях науки, мистецтва, повсякденного життя. Виховувати національну свідомість, гордість за досягнення українців в науці, мистецтві.

Обладнання:   Комп’ютерна презентація із завданнями та ілюстраціями архітектурного мистецтва, живописного мистецтва українських митців та митців світу, струнний музичний інструмент бандура.

 

Хід уроку:

(На екран проектується тема уроку “Порядок і гармонія”  та портрет Піфагора)

I. Мотивація навчання. Ми сьогодні з вами помандруємо до знаменитої давньогрецької школи Піфагора. Учні цієї школи гордо іменували себе піфагорійцями, настільки сильно вони любили і поважали свого учителя. Девізом у цій школі були  “Порядок і гармонія”. Ці слова, а також слова сумірність, узгодженість замінювали сучасний термін пропорція (слова проектуються на екрані). Цей термін появився значно пізніше в математиці і став означати  рівність двох відношень. А  от слова – гармонія,  сумірність, узгодженість – до цього часу побутують в мистецтві, архітектурі (демонструються ілюстрації архітектурних споруд України та країн світу ).

З пропорціями люди пов’язували уявлення про красу, порядок і гармонію, про співзвучність акордів - у музиці.

Піфагор був визначним математиком. Але мало хто знає, що він був також і прекрасним музикантом. Він першим здогадався про залежність між струною і мелодією.  Для цього він створив однострунний інструмент монохорд і провів багато експериментів. Встановив , що чим довша струна, тим звук нижчий, чим коротша – вищий. А чим товща струна, тим звук нижчий, чим тонша – тим вищий (демонструється на струнному інструменті).  Згодом  монохорд Піфагора перетворився в домри, балалайки, гітари, гуслі, бандури, органи, піаніно. За допомогою цих інструментів люди створюють чарівні мелодії, які поліпшують нам настрій.

 Вчення про відношення і пропорції древні греки ще називали музикою. Вони вважали, що чим слабше натягнуто струну, тим нижчий, „товщий” звук вона дає, а чим тугіше натягнуто струну, тим звук вищий (демонструється на струнному інструменті). Але на музичному інструменті не одна, а декілька струн. Щоб усі вони звучали узгоджено, їх довжини повинні перебувати в певному відношенні. Тому вчення про відношення та пропорції у греків було музикою.

 ( Звучить фрагмент української пісні у виконанні учениці на бандурі).

А ось як художники умовно поділили постать людини на пропорційні відрізки (Демонструється на екрані).  Такий умовний поділ допомагає художникам і скульпторам відтворювати людину на полотні і в скульптурі достовірно, правдиво, пропорційно. (На екрані  картини портретного жанру художників України, світу, скульптури). У своїх роботах художники постійно розв’язують математичну задачу про пропорційний поділ.

II Актуалізація опорних знань.

Змагання найрізноманітніші, як розумові так і фізичні дуже полюбляли піфагорійці. Їхній учитель Піфагор навіть був учасником і переможцем на Олімпійських іграх з кулачного бою.

Отже сьогодні як ви зрозуміли ми будемо з вами працювати в школі піфагорійців з пропорціями. А щоб веселіше і цікавіше було повторювати, розв’язувати задачі розділимось на дві команди, які матимуть назви “Порядок” і “Гармонія”. Капітани команд розпочнуть гру ,підготувавши тим самим команду до змагання. Отже, вперед!

1. Конкурс теоретиків.

• Яка рівність називається пропорцією?      1бал
• Як записати пропорцію в буквеному вигляді?    1бал
• Як називаються члени пропорції?       2бали
• Основна властивість пропорції.      2бали
• Як знайти невідомий крайній член пропорції?   3бали
• Як знайти невідомий середній член пропорції?    3бали
• Яка залежність називається оберненою пропорційністю?  4бали
• Яка залежність називається прямою пропорційністю?   4бали

(Учасники по черзі вибирають запитання для супротивника, слухають відповідь і погоджуються з нею або ні. У разі вірної відповіді обох команд вони отримують відповідний бал, якщо один з них помиляється, то отримує бал супротивник).

2. Конкурс “Хто швидше”  (завдання на екрані)

Від кожної команди до дошки виходить один учень і за одну хвилину потрібно підібрати якнайбільше пар відношень, щоб вони утворили пропорцію. Кожна правильна пара приносить бал команді.

1:3   16 :6   8,5:1    1:5   11:18    9:5    63:35    5:15   8: 3    0,3:1,5   2,2 :3,6   17: 2

3. Конкурс “Розв’яжи рівняння” (завдання на екрані)

 Двом учасникам на картках пропонується по дві пропорції на знаходження невідомого члена пропорції.

1 команда

•                  45:18 = 180:X
•                  3,5:6,3=X:0,9

2 команда

•                  75:9= X:27
•                  1,8:1,2=7,2: X

II Розв’язування текстових задач (завдання на екрані)

В школі піфагорійців учні розв’язують найрізноманітніші завдання з різних галузей науки, побуту, мистецтва. Отже і ми спробуємо хоч частинку таких задач розв’язати.

За кожну вірно розв’язану задачу команда отримує 3 бали, за помилку в обчисленнях знімається 1 бал.

Задача 1. Як визначити чи з одного металу виготовлені два бруски, якщо відомо, що маса одного 400 г і об’єм 125см.куб., а другий має масу 820 г і об’єм 225 см.куб.? (пряма пропорційність)

Хвилина  відпочинку. В школі Піфагора велика увага приділялась фізичному розвитку поряд з розумовим. Отже, трішки перепочинемо після розумової праці.(Звучить музика, учні виконують нескладні вправи для відпочинку, релаксації )

Задача 2. Для виготовлення посуду часто використовують сплав під назвою мельхіор. Із мельхіору виготовляють чеканку. Це сплав двох металів – нікелю і міді у відношенні 2:9. Скільки потрібно взяти кожного металу окремо, щоб виготовити 165 кг мельхіору?      (пропорційний поділ)

Задача 3. Бігун подолає дистанцію за 3хв, якщо бігтиме зі швидкістю 40км\год. За скільки він пробіжить цю дистанцію, якщо  збільшить швидкість на 5км\год?    (обернена пропорційність)

Задача 4.  Для натирання паркету  готують спеціальну мастику із крейди, спеціального цементу, оліфи у відношенні 47: 17: 36. Скільки потрібно взяти крейди і оліфи, якщо є 51кг цементу?

( Задачу розв’язати кількома способами, за кожен 2 бали )

III Підведемо підсумки сьогоднішнього уроку – гри. Переможцями стали сильніші в знаннях з математики, сміливіші , наполегливіші та спритніші і дружніші. Бажаю вам подальших успіхів, а всім хороших знань, умінь і навичок, бо без них перемога не можлива.

«Тимчасова невдача краще тимчасової удачі»

                                                    (Піфагор Самоський)

Вечір математики

 «Спочатку було слово»

«Єдина справжня розкіш – це

розкіш людського спілкування»

Екзюпері

Математика – одна з древніх наук, основа всіх наук. Адже це і логіка, і вміння доводити істину, і аналіз, і синтез. За допомогою математики можна дослідити і пояснити явища в природі. Недарма її називають царицею наук.

До чого ж тут «слово» запитаєте ви. А тому, що воно було першим. Воно основа пояснення будь-чого. Математики з часом навчились стисло висловлювати свою думку. Красиво і лаконічно. А спочатку пояснення були досить громіздкими. Та потім довгі пояснення помістились в ємкі слова. Знаючи їх значення, зміст, походження можна  розуміти мову математики.

Хочеться, щоб ви для себе відкрили з іншого боку цю древню науку. Запрошуємо до відкриття. Радійте кожній удачі, кожному маленькому відкриттю. Нехай його до вас уже відкрили, але ж сьогодні це ви зробите для себе. Навчіться знаходити втіху від маленьких перемог над собою і великі успіхи вам забезпечені. Удачі вам!

Напередодні

була оголошена заочна вікторина та пропонувався кросворд. Сьогодні ми розкриємо правильні відповіді і назвемо переможців.

 

Вікторина

 « Чи знаєш ти свій підручник?»

1. Як називається мистецтво розв’язувати рівняння?

(Алгебра)

2. Як записати сучасною мовою алгебри вираз часів Франсуа Вієта1С – 8Q + 16N aequ 40 ?

( x³ – 8x² + 16x = 40 )

3. Що з латинської означає слово «функція»?

(Виконання, звершення)

4. Яка формула скороченого множення звучала в ІІІ ст. до н.е. так: «Якщо пряма лінія як-небудь розсічена, то квадрат на всій прямій дорівнює квадратам на відрізках разом з удвічі взятими прямокутником, що міститься між відрізками» ?

( (a + b)² = a² +2ab + b² )

5. Хто ввів терміни «абсциса, ордината, координати» ?

( Лейбніц )

6. Як в сучасній мові звучить грецький вираз «рахунок камінцями» ?

( Калькулятор )

7. У стародавньому Китаї – «суан-чан», в Японії – «сора бан» а в Росії – «.?.»

(Рахівниця)

8. Як латинською мовою звучить «рух вперед» ?

(Прогресія) 

9. В 9 річному віці майбутній математик Гаусс помітив закономірність, яка властива арифметичній прогресії, коли розв’язував приклад. Що це за приклад?

( 1+2+3+...+98+99+100)

10. Перекладіть на грецьку мову «вимірювання трикутників».

( Тригонометрія)

11. Назвіть три значення слова «дріб».

( Дріб, як число. Барабанний дріб. Дріб для рушниці.)

12. Що в перекладі з грецької означає слово «математика»?

( Наука )

13. Що означає префікс «діа» в словах діагональ, діаметр?

( Через )

Кросворд

 «Видатні математики»

1.               Автор книги  «Начала», яка з 1482 витримала понад 500 видань багатьма мовами світу.

( Евклід)

2.               Український математик, товариш Т.Г.Шеченка та шанувальник його творів.

( Остроградський )

3.               Грецький геометр, в «Арифметиці» якого появилась алгебраїчна символіка, хоч і не зовсім досконала.

( Діофант)

4.               Цей математик встановив, що між довжиною струни і висотою звуку існує прямо пропорційна залежність.

( Піфагор )

5.               На думку цього французького математика, мислення і мова є ознакою душі людської.

(Декарт)

6.               Разом з Ньютоном він блискуче розв’язав теорію нескінченно малих величин, якою займались математики століттями.

( Лейбніц )

7.               Метальні машини, система дзеркал та інші винаходи цього математика наводили жах на римських завойовників під час другої Пунічної війни.

( Архімед )

8.               Німецький астроном і математик, який склав тригонометричні таблиці високої точності.

(Регіомонтан)

9.               Його надгробок прикрашає правильний 17-ти кутник, який він побудував циркулем і лінійкою 19-річним юнаком.

( Гаусс)

10.          «Якщо я бачив далі, ніж інші, то це тому, що я стояв на плечах гігантів».

Кому належать ці слова?

(Ньютон)

11.          За рік він склав екзамени з усіх обов’язкових предметів університету, щоб решту часу присвятити математиці. Хто цей математик?

(Абель)

12.          Його «Рубайят» - класичний твір персько-таджицької поезії. Хто цей математик?

( Омар Хайям)

13.          Він самостійно обчислив висоту єгипетських пірамід за їх тінню, чим немало здивував єгипетського фараона Амадісса.

(Фалес)

14.          Хобі цього математика – розшифровування загадкових, таємних записів. Це допомогло розкрити зміст таємних листів іспанців під час війни Франції з Іспанією.

(Вієт)

15.          Німецький математик Гаусс вивчив російську мову лише для того, щоб вивчати в оригіналі праці цього геніального математика. Хто він?

(Лобачевський)

16.          Твори, що знаєш, роби, що повинен, що буде, те й буде». Хто автор цього математичного твору, за який преміябула збільшена з 3000 до 5000 франків.

( Ковалевська)

17.          Першу орбітальну станцію «Луна-16», що доставила на Землю місячний  ґрунт. Створено на основі теоретичних обґрунтувань цього ученого.

( Келдиш)

 

Завдання

 для гри, яка проводиться у формі брейн - рингу

1.               Хто був автором першого підручника з арифметики на Русі? Ломоносов назвав цей підручник «воротами своєї вченості» ?

 (Магницький )

2.               Сформулюйте твердження протилежне до такого: «Всі прості числа – непарні».

(Деякі прості числа – парні)

3.               Що спільного між геометрією і Шерлоком Холмсом?

(Логічний ланцюжок доведення істини)

4.               Чим відрізняється зображення кута в геометрії від зображення куба на художньому рисунку?

(В геометрії паралельні ребра зображуються паралельними відрізками. А на рисунку художника деякі ребра в уявному продовженні повинні зійтися в одній точці )

5.               Що спільного між цирком і кресленням?

(Цирк, циркуль – коло)

6.               Символом якого числа була квітка лотоса у стародавньому Єгипті і Китаї?

(1000 )

7.               Яке число пов’язує музику і живопис ?

(Сім  основних кольорів, сім  основних нот )

8.               Який квадрат називають круглим?

(Ринг має форму квадрата, але в перекладі це слово означає круг)

9.               Відомо, що 5 в квадраті 25, 10 в квадраті 100. Чому дорівнює кут в квадраті?

 (90 градусів)

10.          Єгиптяни наділяли сторонам прямокутного трикутника властивості чоловіка, дружини і дітей. Яка сторона кому відповідає на вашу думку? Плутарх писав, що єгиптяни порівнювали природу Всесвіту з трикутником.
11.          Замініть речення математичним терміном

•                 Частина січної всередині кола    (Хорда)
•                 Многокутник з найменшою кількістю сторін ( Трикутник)
•                 Хорда, яка приходить через центр кола ( Діаметр )
•                 Рівнобедрений трикутник, у якого бічна сторона дорівнює основі.

(Рівносторонній трикутник )

•                 Два кола нерівних радіусів зі спільним центром

(Концентричні кола)

12.          Я задумала число від 1 до 1000. Спробуйте з десяти запитань, на які треба відповідати «так» чи «ні», відгадати задумане число.
13.          Є 8 монет однієї вартості. Серед них одна – фальшива – легша за решту. Є терези без гирьок. За двома зважуваннями виявити фальшиву монету.

В кінці гри кожній команді дають набір слів розрізаних крилатих висловів і їх авторів. Скласти ці вислови. Бал команді, яка зробить це першою.

Вислови

1. У людей, які засвоїли великі принципи математики , одним органом чуття більше.

Ч. Дарвін

2. Хто не знайомий із законом руху, той не може пізнати природу.

Г.Галілей

 

 

Позакласний захід з математики

„І жартома і всерйоз”

„Предмет математики є настільки

серйозним, що корисно не нехтувати

можливістю зробити його дещо цікавішим”

Блез Паскаль

 

 

Вступ

 М.В.Гоголь вважав, що оця всюдисуща лінь заважає людям стати великими. А в казці Кіплінга за лінощі верблюд був покараний горбом на спині. А в казках ...

Та що ми вас переконуємо. Ви самі все знаєте. Вам про це говорять щодня батьки, вчителі, вихователі. Ми ж хочемо розкрити вам іншу сторону лінощів, їх секрет. Хіба ж можна їх засуджувати? Вони ж  - двигун прогресу! Подумайте тільки – лінощі допомагали людям придумати пилосос, пральну машину, посудомийну машину, калькулятор, та в кінці-кінців – комп’ютер. Розумні люди вважають, що лінощі – це засіб від рутинної безкорисної праці, вони спонукають до думки про полегшення життя.

Ну як, ми вас надихнули? Давайте, думайте, та не переборщіть. Не так давно хитромудрі японці відкрили секрет довголіття клітин мозку. Знаєте що потрібно робити, щоб мозок не старів? Це тільки подумати! Це не просто слова – це керівництво до дії: „ Якщо хочете не зістаритись, не стати склеротиком в розквіті сил – частіше думайте!”

Тримати мозок в робочому стані можна різними способами, та сьогоднішній – найприємніший. Ми пропонуємо гру.

Китайці говорять, що шлях осилює той, хто іде, і кожна велика дорога починається з маленького кроку. Перший крок ви вже зробили – прийшли на гру. А тепер – ламайте голови, ворушіть звивинами, заставляйте працювати мозок  і - перемога забезпечена.

Отже – гра!

Для лінивих і смішливих,

Для розумних і кмітливих,

Для рискових знатаків,

Для усіх, хто загорівсь.

 

Перший тур

„ Заведи дружбу з противником”

(представлення команд)

 

 

 

 

 

 

 

 

Команда 10 класу

 

 

 

 

 

 

 

Команда 11 класу

 

Другий тур „Для лінивих”

(розминка)

1. Коли займаються обчисленнями на птахофермі?

(Восени)

2. Яку геометричну фігуру вивчає покарана дитина?

(Кут)

3. Яка геометрична фігура іноді виникає в коханні?

(Трикутник)

4. Скільки героїв збирали урожай в казці „Ріпка”?

(6)

5. Скільки коштує книжка з казки Андерсена „Дикі лебеді”

(Пів королівства)

6. На скільки основних груп поділяються музичні інструменти?

(5, струнні, клавішні, ударні, мідні духові та дерев’яні духові)

7. Як називається відрізок шляху довжиною 42км195м?

(Марафонський)

8. Який спортивний снаряд складається з двох циліндрів?

( Граната)

9. Пожежник одягає штани за 3с. скільки штанів він може переодягнути за 5хв?

( 50)

 

Третій тур „WWW”

What?  Where?  When?

(Запитання звідусіль)

1. Зазвичай місяць закінчується 30-им або 31 – им числом. В якому місяці є число 28?

(В кожному)

2. Маленький Блез Паскаль сформулював деяку теорему так: „ Три кути таткового капелюха дорівнюють двом кутам стола”. Сформулюйте цю теорему.

(Сума кутів трикутника дорівнює 180 градусів)

3. Ці тіла Аль Хорезмі називав „круглий паралелепіпед, кругла піраміда”. Що це за тіла?

( Циліндр і конус)

4. Яку науку спонукав розлив Нілу?

(Геометрію)

5. Що просіюють через решето в математиці? Як воно називається?

( Прості числа через решето Ератосфена)

6. Метал з якого виливають медалі для почесного третього місця.

( Бронза)

7. Статус мільярда.

(Число)

8. Для циркового акробата – це робочий інструмент, для решти – геометрична фігура.

( Трапеція)

 

Четвертий тур „Для смішливих”

Американці вважають, що сміх надзвичайно корисний і для тіла, і для душі. На їх думку, коли людина сміється, то через горло повітря виривається зі швидкістю 70 миль за годину. В крові починає пульсувати адреналін, з легень виходить вуглекислий газ, очі промиваються сльозами від сміху. А французи відкрили, що 1хв сміху рівноцінна 45хв іншого способу відпочинку. Австрійська спілка боротьби з депресією недавно випустила компакт-диск, який повинен допомагати хворим вилікуватись. Запис сміху на ньому триває 20хв. Простіше кажучи, весь світ згоден із знаменитим польським гумористом Станіславом Єжи Ленцем: Якщо хочеш жити, частіше помирай від сміху”.

Наше наступне завдання для таких реальних або потенціальних довгожителів. Необхідно дотепно закінчити коротке оповідання. Кожна команда висуває свою версію.

1. - Іванку, розбуди свого сусіда, - каже учитель.

    - А чому я? Це ж ...

(... ви його приспали)

2.  – Хлопчику, скільки тобі років?

     - Шість – удома, сім – у школі, і чотири ...

(  ... в транспорті)

3. Професор на лекції: „Через поцілунок партнеру передається 5 млн. мікробів.”

Студент: „ Але ж іншого боку ...”

( ... скільки ж і віддається)

П’ятий тур „ Капітане, посміхнися! ”

(репетитор)

Для капітанів пропонується веселий рахунок. Вони по черзі повторяють за ведучим набір слів, який він їм пропонує. Члени команди противника можуть смішити в цей час капітана. Його завдання, не зважаючи на них, якнайточніше повторювати.

Огірок	Одеколон
Дві дошки	Два дивани
Три трясучі трамваї	Три товсто лобі телепні
Чотири червиві чорнобокі черешні	Чотири чарівні чистенькі чашечки
П’ять першокласних плоских пастеризованих патисонів	П’ять пеліканів плювалися переспілими помаранчами
Шість шикарних „Шкод” шурхотіли шелестіли шинами	Шість шведських шовковистих шоколадних шиншилових шубок
Сім сорок скрекотали серед стада синіх свиней	Сім сильно синіх симетрично складених солодких сливок
Вісім великих волохатих ведмедів весело вигулювалися весняними вулицями	Вісім великих в’ялих волохатих веселих віників викладені віялом
Дев’ять дятлів довбали дубову дровиняку для дивного дикого деркача	Дев’ять довгих диких дивних дійсно дорогих дощок дибали додому
Десять днів дрімав дикобраз, декілька днів ділив делікатесну добру диню	Десять дивакуватих дубів давним-давно двояться для дезорієнтації дебелих дикунів

 

 

 

 

 

 

 

 

 

Шостий тур „Для своїх”

(театр пантоміми)

Один з учасників команди отримує завдання, готується і показує за допомогою жестів і міміки учасникам своєї команди. їх завдання - розгадати терміни.

І команда

1. Радикуліт.

2. Ділення.

3. Пояс для схуднення.

4. Транспортир.

ІІ команда

1. Наркоман.

2. Парабола.

3. Велотренажер.

4. Циркуль.

Сьомий тур„ Математики жартують”

( Домашнє завдання )

 

 

 

 

 

Сценка «На контрольній»

 

Восьмий тур „Як стати розумним”

(Для допитливих)

1. Петро І добре знав аудицію, субстракцію, мультиплікацію і дивізію. В його час це знали далеко не всі і Петро І настійно заставляв вивчати це своїх подвижників. Зараз це знає кожен школяр. як це тепер називається?

( Додавання, віднімання, множення, ділення)

2. Про який древній пристрій нагадує приказка „З того часу багато води збігло”?

( Водяний годинник)

3. В Англії на бенкетах на один із стільців клали плюшевого ведмедика і прибирали, коли розходились гості. Що це за стілець?

( № 13)

4. Бікфордів шнур горить 1хв. Як за допомогою 2х шнурів відміряти 45с.?

( Запалити один з шнурів з обох боків, а другий з одного кінця.

 Коли перший згорить, запалити з другого кінця другий)

Ну от і все, гра закінчилась. Надіємось ви дістали задоволення? І помітьте, що все це без особливих зусиль. Адже на навчання ви затрачаєте дуже мало часу. Поміркуйте. Рік має 365 днів. З них 52 дні - неділі, 10 - святкових днів, канікулярних днів - 100. Отже, відпочинку - 162 дні. Вночі ми не навчаємось – це ще половина року  - 182 дні. От і рахуйте, що залишається для навчання всього близько 20 днів. Щодня по 6 уроків – це лише чверть доби. Тобто, ми отримуємо міцні знання лише 5 днів на рік.

Думайте!

А ми послухаємо журі.

 

 

 

Гра „ Я знаю, що нічого не знаю”

 

 

До участі в грі запрошуються по три представники від 9, 10, 11 класів, які учнями своїх класів визнані сильнішими в точних науках, таких як фізика, математика і інформатика. Хоча про себе вони говорять словами відомого філософа „ Я знаю, що нічого не знаю”. Знайомимось з ними. Кращі знавці (на думку однокласників)

З математики: (прізвища учасників)

З фізики: (прізвища учасників)

 З інформатики: (прізвища учасників)

Поближче з учасниками познайомимось  в ході гри.

 

Правила гри

 А зараз до вашої уваги правила, за якими ми будемо грати. Учасники вже обрали собі теми. Гра буде проходити в чотири етапи. Перед кожним етапом відбірковий тур, в ході якого визначається порядок відповіді. В ході кожного етапу визначається один переможець. Перші три етапи визначать першого математика, фізика, інформатика, а на четвертому етапі визначиться кращий знавець точних наук. Переможець отримує поточну оцінку „12” з кожного предмета сьогоднішньої гри, учасники четвертого туру отримують сертифікат „Рятівний бал”, який можна використати по одному разу (добавити до незадовільної оцінки) з кожного з названих предметів у випадку отримання оцінки, яка не задовольняє під час поточного оцінювання. А всі учасники гри отримують сертифікат „Рятівний бал”, який можна використати лише один раз на одному за вибором з названих предметів.

Жеребкування. Визначаємо, в якому порядку будуть змагатися команди знавців математики, фізики, інформатики.

Перший етап, другий і третій етапи змагаються в порядку черги знавці математики, фізики інформатики.

Відбірковий  тур кожного етапу „Вибираємо доріжку”.

Перед вами три доріжки: зелена - з трьома клітинками, жовта – з двома клітинками, червона – з однією клітинкою. За результатом відбіркового туру перший гравець має право вибрати собі доріжку одну з трьох, другий – одну з двох, третьому, що залишиться. Зелена доріжка передбачає три питання з математики, не дуже важких, жовта доріжка – два питання трохи важчих, а червона – одне, але найважче запитання. За кожне запитання першої доріжки можна отримати по два бали, за запитання другої доріжки по три бали, за запитання третьої доріжки можна отримати одразу 6 балів. В разі набирання однакової кількості балів ставиться додаткове питання, яке визначить переможця кожного туру.

В четвертому турі „Універсальна вікторина” визначається переможець гри. Перед учасникам доріжки з однаковою кількістю клітинок, хто першим дійде до краю доріжки, той -  переможець. Кожна клітинка – запитання, завдання, яке треба розв’язати.

Дорогу може подолати лише той, хто йде. Тож, вперед до перемоги! Бажаю успіху.

Запитання для знайомства з учасниками гри

•                  Чому ти обрав дану тему?
•                  Чому на вашу думку предмети точних наук даються важче, ніж гуманітарні?
•                  Яким іграм ви надаєте перевагу: активним чи інтелектуальним?
•                  Чим ви займаєтесь у вільний від уроків і спец занять час?
•                  Що вам дало навчання в нашій школі?
•                  Чи вважаєте ви, що думка дорослих про комп’ютерні ігри, як про зло для дитячої психіки, правильна?
•                  Фізика і побут – це сумісні речі?
•                  Веселка – це розкладання променів світла на кольорову гамму, чи привід радіти життю?
•                  Якій музиці ви надаєте перевагу: комп’ютерній чи живій?

Тур „Знавці  математики”

Відбірковий тур:

Розмістіть теореми, в порядку вивчення їх у школі.

А) Вієта; Б) Піфагора; В) Фалеса

 

Завдання зеленої доріжки:

1.         Скільки морозива можна перевезти п’ятитонним вантажним автомобілем?
2.         Чи є число 2001 простим?
3.         На чию честь названа прямокутна система координат?

Завдання жовтої доріжки:

1.         Якою цифрою закінчується число 5²⁰⁰⁰ ?
2.         Які числа протягом багатьох століть називали абсурдними, фіктивними, „числами диявола”?

Завдання червоної доріжки:

Хто з математиків довів таку теорему: „Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій стороні кута”?

Додаткові питання:

1.         Квадрат суми двох виразів ...
2.         Означення синуса гострого кута прямокутного трикутника.
3.         Третя ознака рівності трикутників.

Тур „Знавці  інформатики”

Відбірковий тур:

Скільки буде 1+1 в двійковій системі числення?

Завдання зеленої доріжки:

1.                     Який пристрій комп’ютера може давати шкідливу дію на здоров’я людини?
2.                     Як називається „мишка”, яка перевернута догори та закріплена на клавіатурі в ноутбуках?
3.                     Як називається будь-який символ інформації?

Завдання жовтої доріжки:

1.                  У Стародавньому Римі використовувалось багато пристосувань для рахунку – пальці Рур, вузли на мотузку, камінчики в жолобку, позначки на паличці. Одне з цих пристосувань називалось „калькулюс”, від якого проходить слово „калькулятор”. Що називалось цим словом?
2.                  Що несе повідомлення, якщо воно не несе корисної інформації?

Завдання червоної доріжки:

Розташуйте  подані ігрові консолі, починаючи з найдавнішої:

А)X-Box, Б) Play Station 1, В)Dandy,  Г) Sega Mega Drive

 

Додаткові питання:

1.                Умовні знаки, за допомогою яких звертають на щось увагу, оповіщають, передають розпорядження або проводять переговори.
2.                Скільки байт містить слово „життя”?
3.                Від чого слід оберігати дискету крім фізичних ушкоджень?

Тур „Знавці  фізики”

Відбірковий тур:

Систематизувати в порядку зменшення такі одиниці маси: кілограм, грам, тонна, центнер.

Завдання зеленої доріжки:

1.Що вимірюється в паскалях?

2. Де вага тіла більша – на Землі чи на Місяці?

3. чому дорівнює прискорення вільного падіння?

Завдання жовтої доріжки:

1.                     Яку енергію має тіло, що швидко рухається?
2.                     Чому маленька бджола створює своїм жалом великий тиск?

Завдання червоної доріжки:

Чому кістки птаха наповнені не кістковим мозком, а повітрям?

 

Додаткові питання:

1.Де швидкість молекул більша - у воді чи в парі?

2. Як називають величину, яка є мірою інертності тіла?

3. Як називається прилад для вимірювання температури?

Тур „Універсальна вікторина”

1.         В якому місці водоспаду температура води найтепліша?
2.         Чому мокрий одяг тісніший?
3.         Що означає символ WWW?
4.         Назвіть повне ім’я математика, який конструював так звану аналітичну машину?
5.         Економічна діяльність, звітність про яку відсутня.
6.         Який трикутник називається єгипетським?
7.         Що міряли у гривнях в стародавні часи?
8.         Як рухається тіло, кинуте вертикально вгору?
9.         Перша обчислювальна машина.

Підведення підсумків

Нагорода переможців

 

Сертифікат

„ Рятівний Бал ”

 

Виданий________________________________________

 

За участь у грі „ Я знаю, що нічого не знаю”, яка проходила ___________ під час проведення тижня точних наук  у школі.

Пред’явник цього сертифікату має право використати його один раз в цьому навчальному році на одному з уроків математики, фізики чи інформатики в разі отримання оцінки, яка його не задовольняє, і добавити рятівний бал до отриманої оцінки.

 

Ведучий гри:

                               Члени журі:

 

 

 

Сертифікат

„ 12 балів ”

Виданий________________________________________

 

За перемогу у грі „ Я знаю, що нічого не знаю”, яка проходила _________під час проведення тижня точних наук  у школі.

Пред’явник цього сертифікату має право використати його один раз в цьому навчальному році на кожному з уроків математики, фізики і інформатики в разі отримання оцінки, яка його не задовольняє, і замінити її на оцінку „12”.

 

Ведучий гри:

                                Члени журі:

СПИСОК ВИКОРИСТОВАНИХ ДЖЕРЕЛ

 

1. Бевз Г.П. Методика викладання математики: Навч.посібник –К.: Вища школа., 1989. -367с.
2. Бич О.В., Григорєва О.В. Застосування інформаційних технологій при вивченні математики. – Кривий Ріг КДПУ,2003р.
3. Борисова В.О. Міжнародний конкурс-гра „Кенгуру - 2002” // Математика – 2003 - № 7, с.18-20.
4. Борисова В.О. Міжнародний конкурс-гра „Кенгуру - 2002” // Математика – 2003 - № 8, с.7-9.
5. Вітюк О.В. Використання засобів новітніх інформаційних технологій навчання під час розв’язання стереометричних задач на обчисленого характеру. // Математика в школі. - 2000.- №5.
6. Глейзер Г.И. История математики в школе: Пособие для учителей. — М.: Просвещение, 1982.
7. Карпінська І.Н. Нестандартні уроки з математики. – Тернопіль,2000.- 48с.
8. Колосов А. А, Книга для внекласеного чтения по математике в старших классах. — М: Учпедгиз, 1963.
9. Підручна М.В., Янченко Г.М. Дидактичний матеріал для уроків - практикум з математики у 5кл.,6кл.- Тернопіль: Підручники і посібники, 2006-64с.
10. Фридман Л.М., Турецкий Е.М.Как научиться решать задачи.: Кн. для уч-ся ст. классов  сред. шк. – М.: Просвещение,1989.-192с.
11. Янченко Г.М. Сучасні уроки з математики. – Тернопіль, 1991.-26с.