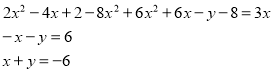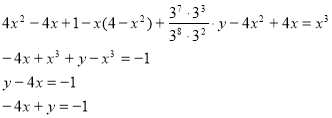Математика в одній задачі. Підготовка до ЗНО
При підготовці до ЗНО кожен учень задається питанням : «Як
швидко повторити курс алгебри чи геометрії 7 або 8 класу, якщо
на черзі ще інші предмети?»
І тут я пропоную учням всього одну задачу:
Геометрія 7 класу в одній задачі:
Для пари паралельних прямих a i b проведено січну с, яка перетинає дані прямі в т. А і D відповідно. З т. С![]() b (т. С≠D) проведена пряма, яка проходить через т. О – середина АD і перетинає а в точці В. У ΔВАО кути відносяться як 1 : 2 : 3. Знайти градусні міри кутів ΔСОD, довжину відрізків ОD і DС, якщо ВА = 14см.
b (т. С≠D) проведена пряма, яка проходить через т. О – середина АD і перетинає а в точці В. У ΔВАО кути відносяться як 1 : 2 : 3. Знайти градусні міри кутів ΔСОD, довжину відрізків ОD і DС, якщо ВА = 14см.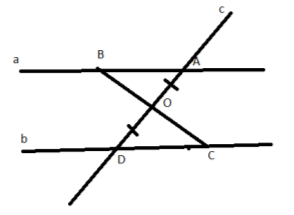
Розв’язання:
- Розглянемо ∆ВАО,
![]() , нехай k= x, тоді
, нехай k= x, тоді ![]() Оскільки сума кутів любого трикутника дорівнює 180°, то маємо рівняння:
Оскільки сума кутів любого трикутника дорівнює 180°, то маємо рівняння:
х + 2х +3х = 180°
6х = 180°
х = 180° : 6
х =30°
Тоді: ![]() .
.
- ОА =ОD – за умовою;
![]() ВОА =
ВОА = ![]() ODC – як вертикальні;
ODC – як вертикальні;
![]() ВАО =
ВАО = ![]() ОDC – як внутрішні односторонні при двох паралельних прямих а і b та січній с.
ОDC – як внутрішні односторонні при двох паралельних прямих а і b та січній с.
Тому ∆ВОА = ∆ОDC за стороною та прилеглими кутами. Як відомо, у рівних трикутників відповідні кути і сторони рівні.
Отже, ВА = DC = 14 см, ![]() В =
В = ![]() С = 30°,
С = 30°, ![]() А =
А = ![]() D =60°,
D =60°, ![]() О = 90°.
О = 90°.
-
Розглянемо ∆ ODC:
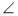 D = 90°,
D = 90°,  С = 30°, DC – гіпотенуза прямокутного трикутника і дорівнює 14 см. Як відомо, в прямокутному трикутнику навпроти кута 30° лежить катет, який дорівнює половині гіпотенузи.
С = 30°, DC – гіпотенуза прямокутного трикутника і дорівнює 14 см. Як відомо, в прямокутному трикутнику навпроти кута 30° лежить катет, який дорівнює половині гіпотенузи.
Отже, ОD = ![]() DC; ОD = 14 : 2 = 7 см.
DC; ОD = 14 : 2 = 7 см.
Підсумок. Задача розв’язана. Які ж основні елементи ми використовували?
-
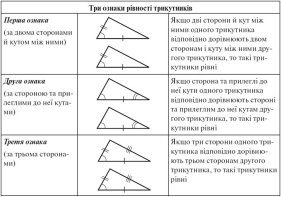 Рівність трикутників. Якщо ви це згадали, то тоді як бонус – всі елементи одного трикутника дорівнюють усім елементам другого трикутника. А також дуже важливим у цієї теми є поняття відповідність сторін і кутів.
Рівність трикутників. Якщо ви це згадали, то тоді як бонус – всі елементи одного трикутника дорівнюють усім елементам другого трикутника. А також дуже важливим у цієї теми є поняття відповідність сторін і кутів.
-
 Використали одну з найважливішу теорему про суму кутів трикутника.
Використали одну з найважливішу теорему про суму кутів трикутника.
- Повторили задачі на пропорційний поділ.
-
 Використали властивість паралельних прямих і січної та утворених куті
Використали властивість паралельних прямих і січної та утворених куті
- Ще використали властивість прямокутного трикутника, у якого один кут дорівнює 30°.

Геометрія 8 класу в одній задачі:
У чотирикутнику АВСD (ВС ││АD), ВС = 8см, а бісектриса кута D попадає у точку В і утворює зі стороною ВС кут 30°, а з бічною стороною АВ - кут 90°. Знайти відстань від точки В до АD, діагональ ВD, площу даного чотирикутника АВСD.
 Розв’язання:
Розв’язання:
Зверніть увагу на умову, тут не говориться про вид чотирикутника. Зробимо аналіз умови. Важко розуміти задачу без малюнка. Проведемо дві паралельні прямі ВС і АD. Ось що ми отримали. Пригадаємо, що тільки у чотирикутника-трапеції дві сторони паралельні.
- Так як ВС ││ АD (за умовою), то чотирикутник АВСD – трапеція.
-
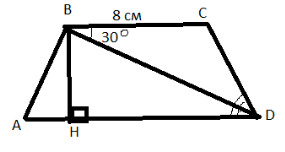 Пригадаємо, що називається відстанню від точки до прямої. Якщо у нас є деяка точка і ми хочемо з неї «попасти» на деяку пряму, то це буде найкоротша відстань. Відстанню в математиці називають довжину перпендикуляра, це є самий короткий шлях. Отже, шукана відстань ВН.
Пригадаємо, що називається відстанню від точки до прямої. Якщо у нас є деяка точка і ми хочемо з неї «попасти» на деяку пряму, то це буде найкоротша відстань. Відстанню в математиці називають довжину перпендикуляра, це є самий короткий шлях. Отже, шукана відстань ВН.
-
Використаємо паралельність прямих ВС і АD, ВD – січна, то
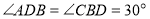 - як внутрішні різносторонні, а так як DВ – бісектриса, то
- як внутрішні різносторонні, а так як DВ – бісектриса, то 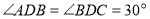 . Ми тепер можемо знайти
. Ми тепер можемо знайти 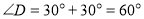 .
.
- Розіб’ємо дану фігуру на менш прості. А що може бути простіше трикутника? ВСD трикутник, у якого кути при основі рівні. Це можливо лише у рівнобедреного трикутника. Бічні сторони прилеглі до рівних кутів. ВС = СD = 8 см.
-
Розглянемо ∆ АВD:
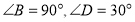 , тоді
, тоді 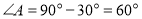 . Нагадую, що в прямокутному трикутнику на два гострих кута припадає 90°.
. Нагадую, що в прямокутному трикутнику на два гострих кута припадає 90°.
У трапеції ![]() , тому трапеція АВСD рівнобічна, АВ = СD =8 см.
, тому трапеція АВСD рівнобічна, АВ = СD =8 см.
-
Розглянемо ∆АВН,
 Н=90°, за тригонометричним співвідношенням маємо:
Н=90°, за тригонометричним співвідношенням маємо:
ВН = 8·sin60° = 8· ![]() см. За т. Піфагора: АН =
см. За т. Піфагора: АН =![]() = 4см.
= 4см.
- За метричним співвідношенням в прямокутному трикутнику АВD маємо:
ВА2 = АН · АD
64 = 4 · АD
АD= 16 см.
-
Розглянемо ∆АВD і ∆АВН,
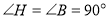 ,
, 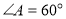 - спільний.
- спільний.
Отже, ∆АВD ~ ∆АВН за двома кутами. Якщо трикутники подібні, то можна скласти пропорцію відповідних сторін:
![]() ,
, ![]() , BD =
, BD = ![]() см.
см.
-
Площу трапеції знайдемо за формулою:
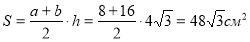 .
.
Підсумок. Які головні теми ми повторили, розв’язавши всього одну задачу?
- Розглядали різні види чотирикутників (паралелограми, прямокутники, ромби, квадрати, трапеції) і встановили потрібний вид чотирикутника.
-
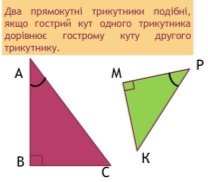 Розібралися з подібними трикутниками.
Розібралися з подібними трикутниками.
- Розглянули пропорційні відрізки у прямокутному трикутнику.
- Пригадали що таке sin, cos, tg, ctg, які використовують лише в прямокутному трикутнику.
Тепер вся геометрія 8 класу у вас в кишені!
Алгебра 7 класу в одній задачі:
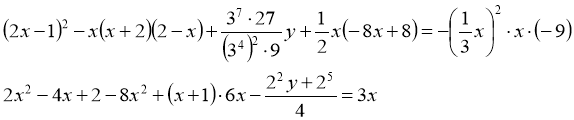
![]()
(1)
(2)
Розв’язати дану систему рівнянь усіма способами.
Спочатку спростимо кожне рівняння. Позначимо їх (1) і (2):
2.
Маємо систему рівнянь:
![]()
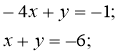
- Розв’яжемо дану систему способом підстановки. Для цього виразимо в першому рівнянні одну змінну через іншу:
![]()
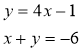 Підставимо вираз
Підставимо вираз ![]() у друге рівняння замість у:
у друге рівняння замість у:
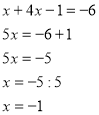
![]()
Відповідь: (-1;-5)
- Розв’яжемо дану систему способом віднімання. Для цього від (1) – (2):
![]()
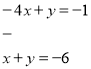
_____________
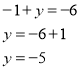
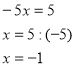 Підставимо знайдено значення х у друге рівняння :
Підставимо знайдено значення х у друге рівняння :
Відповідь: (-1;-5)
3. Для розв'язання системи графічним способом будують графіки всіх рівнянь, які входять в систему. Координати точок перетину є розв'язком цієї системи.
![]()
![]() Графічний спосіб є зручним для знайдення числа розв'язків системи (тобто скільки точок перетину графіків, стільки й розв'язків має система), але не зручний при обчисленні координат точок (тобто значення координат можна отримати лише наближені).
Графічний спосіб є зручним для знайдення числа розв'язків системи (тобто скільки точок перетину графіків, стільки й розв'язків має система), але не зручний при обчисленні координат точок (тобто значення координат можна отримати лише наближені).
Виразимо одну змінну через іншу:
Щоб побудувати графіки лінійних функцій в одній системі координат, нам потрібні координати двох точок, що належать графікам функцій.
Складемо таблицю значень функцій:
|
х |
-1 |
1 |
|
у |
-5 |
3 |
|
х |
-3 |
1 |
|
у |
-3 |
-7 |
Побудуємо графіки лінійних функцій в одній системі координат:
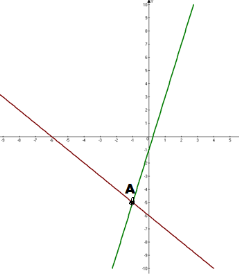
Ці прямі перетинаються в точці А(-1;-5). Координати цієї точки одночасно є розв’язком і першого і другого рівнянь системи:
![]()
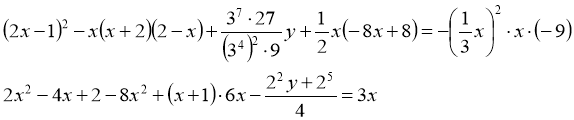
Іноді в задачах просять не розв’язувати систему, а встановити скільки розв’язків має система. Як це зробити не будуючи графіки?
![]()
![]() Кількість розв’язків системи лінійних рівнянь
Кількість розв’язків системи лінійних рівнянь
можна визначити за співвідношенням коефіцієнтів.
Якщо ![]() , то система має безліч розв’язків.
, то система має безліч розв’язків.
Якщо ![]() , то система не має розв’язків.
, то система не має розв’язків.
Якщо ![]() , то система має один розв’язок.
, то система має один розв’язок.
Алгебра 8 + 9 класи в одній задачі:
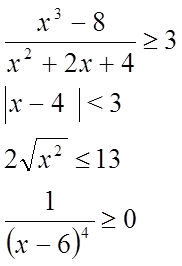
![]()
(1) Позначимо кожну нерівність (1), (2), (3), (4) та розв’яжемо їх окремо.
(2)
(3)
(4)
![]() ДОЗ:
ДОЗ: ![]() ; D = b2 – 4ac = 4 – 16 = -12<0
; D = b2 – 4ac = 4 – 16 = -12<0
Даний тричлен розв’язку не має. При любих значеннях х знаменник ≠ 0.
![]()
- │х - 4│< 3
-3 < х – 4 < 3
-3 + 4 < х < 3 + 4
1 < х < 7
-
2
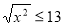
2 │х│≤ 13
│х│≤ 6,5
-6,5 ≤ х ≤ 6,5
4. ![]() , ОДЗ: R, крім х – 6 ≠ 0, х ≠ 6.
, ОДЗ: R, крім х – 6 ≠ 0, х ≠ 6.
![]() Отже, дана система має вигляд:
Отже, дана система має вигляд:
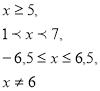
Побудуємо розв’язки кожної нерівності на координатній прямій :
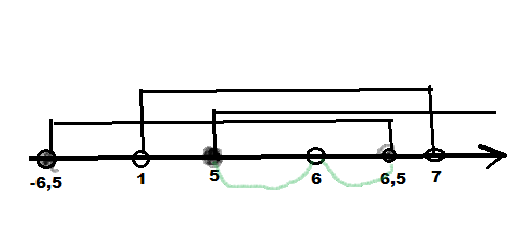
Відповідь: [5; 6) ![]() (6; 6,5).
(6; 6,5).
Якщо все засвоїли, то домашнє завдання:
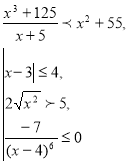


про публікацію авторської розробки
Додати розробку