ВІДДІЛ  ОСВІТИ   ПЕРЕМИШЛЯНСЬКОЇ   РАЙДЕЖАДМІНІСТРАЦІЇ

Методичний кабінет

Дунаївська загальноосвітня школа                   І-ІІІ ступенів

 

 

 

 

 

О. Я. Федак

 

 

АКТИВІЗАЦІЯ НАВЧАЛЬНО - ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ НА УРОКАХ МАТЕМАТИКИ

(З ДОСВІДУ РОБОТИ)

 

 

 

                    Дунаїв - Перемишляни  2015р.

Федак Ольга Ярославівна                Активізація навчально–пізнавальної діяльності на уроках математики.(методичні рекомендації)

Дунаївська ЗОШ І-ІІІ ступенів, 2015- 35ст.

У збірнику розкрито форми і методи активізації пізнавальної діяльності учнів на уроках математики, а також розкрито застосування комп’ютерних технологій використовуючи ППЗ .

 

Матеріали зібрала і упорядкувала вчитель математики Федак О.Я.

 Рецензент: Л.М. Лобод як – методист РМК.

 

 Схвалено та рекомендовано на засіданні методичної ради відділу освіти

Перемишлянської РДА від 23 лютого 2015р., протокол №1

 

Відповідальна за випуск: Тарасюк С.А., завідуюча

                                           методкабінетом

                        відділу освіти Перемишлянської

                                райдержадміністрації.

 

 

 

Комп’ютерна верстка: О.Я.Федак

Друк: 3 примірники.

Електронний варіант

 

 

 

 

 

                                                                                                                                                                    « Але найбільш чарує математика

                                           бездоганною, неспростовною

                                                               логікою своїх глибоко                                                                         продуманих теорій,

                                                       стрункість і витонченість яких                                                                         

дають її любителям велике естетичне  задоволення.                Саме в цій особливості

                                                            математики криється її привабливість»

                                                                                                                                 О.С.Сморжевський

 

В С Т У П

       Визнаною у всьому світі є провідна роль шкільної математичної освіти у системі загальної освіти, її значення для розвитку і виховання молоді, для формування інтелектуального потенціалу суспільства. Математика завжди і у всіх країнах була і є невід’ємним елементом системи загальної освіти. Якість математичної освіти є одним із важливіших факторів економічного і суспільно – політичного розвитку країни.

       Стратегічною метою математичної освіти в загальноосвітній школі є розвиток і саморозвиток школярів шляхом оволодіння математичними знаннями і видами діяльності, забезпечення математичної грамотності особистості для її соціалізації і професіоналізації. У постіндустріальному, інформаційному суспільстві, до якого прямує Україна, інтелектуальний  потенціал його членів складає національне багатство. У такому суспільстві від рівня інтелекту особистості і здатності до саморозвитку залежить успішність її соціалізації і самореалізації.

      Математична освіта робить вагомий внесок у розвиток і саморозвиток інтелекту особистості в цілому. Вона має величезні можливості для формування навичок чіткого і логічного мислення, виразного мовлення.

      Виходячи з принципу розвитку, метою навчання є виховання суб’єкта власного життя, суб’єкта навчання, тобто людини, здатної самостійно знаходити способи розв’язання поставлених перед нею навчальних завдань, здатної до само зміни і саморозвитку.

      Однією з основних проблем навчання є формування в дитини пізнавального інтересу. За допомогою примусу або оцінок неможливо перетворити навчання на захоплюючий процес пізнання. Є чимало дітей, які «бояться математики», упереджено ставляться до цього предмета.

      Зацікавити учнів математикою, показати її могутність і красу, примусити полюбити її – завдання кожного вчителя математики. Він повинен навчити учнів бачити глибину і стрункість логічних міркувань у математиці і тим самим поступово розкрити їм ще один бік краси і сили математики, про який досить образно говорив професор О.С. Сморжевський: «Але найбільш чарує математика бездоганною, неспростовною логікою своїх глибоко продуманих теорій, стрункість і витонченість яких дають  її любителям велике естетичне задоволення. Саме в цій особливості математики криється її привабливість».

      Головним напрямком у викладанні математики є викладання математики як засобу мислення учнів. Методика викладання випливає з того, що є метою навчання, спирається на вікові особливості учнів та на розуміння причин, що гальмують сприйняття відповідного матеріалу.

Своє завдання, як вчителя я розумію насамперед у вихованні учня як активно мислячої особистості, що зможе творчо підійти до матеріалу, який вивчається. Тому я працюю над проблемним питанням “ активізація навчально- пізнавальної діяльності учнів на уроках математики”. Загальний смисл вимоги активної навчально-пізнавальної діяльності учнів полягає в тому, що ця вимога має два аспекти: внутрішній ( психолого-педагогічний) і зовнішній (організаційний).

Внутрішній аспект активної навчальної діяльності школярів полягає в тому, що вона визначається такими компонентами, як інтерес до навчання, ініціативність у навчальній роботі, пізнавальна самостійність, напруження фізичних і розумових сил для розв’язання поставленої пізнавальної задачі. Розвиток цих компонентів і складає необхідну умову організації активної навчально-пізнавальної діяльності учнів.

Зовнішній аспект активної навчальної діяльності школярів полягає в тому, що до цієї діяльності необхідно залучити всіх учнів даного класу і кожного з них.

Ця вимога може бути здійснена тільки з допомогою умілого поєднання фронтальної, групової, індивідуальної роботи учнів, а також за допомогою сучасних засобів індивідуального навчання. такими засобами є дидактичні матеріали з друкованою основою, карточки-інструкції, карточки-зразки, засоби програмованого контролю і т.д. Провідні ідеї мого творчого підходу до праці такі: зацікавлення учнів навчальним матеріалом і процесом оволодіння ним та раціоналізація навчальної діяльності учнів. Реалізую ці ідеї методами: словесним, наочним, практичним проблемним, дослідницьким.

Насамперед звертаю увагу на розвиток пізнавального інтересу учнів. Ця особиста риса школяра проявляється у вигляді допитливості, активності, цілеспрямованості.

Для правильної організації роботи по формуванню в учнів пізнавального інтересу за допомогою прогностичних методів виявляю “за” і “проти”, які впливають на цей процес. Маючи такі дані, будую свою роботу так, щоб знімаючи негативні фактори, цілеспрямовано формувати у школярів пізнавальний інтерес. При цьому намагаюся оптимально поєднувати методи як суб’єктивного характеру, так і об’єктивного. Суб’єктивний шлях організації навчальної діяльності - це методи переконання, пояснення, інформування. Об’єктивний - створення умов, у яких в учня виникли б мотиви до навчальної діяльності, щоб він почав діяти. І тоді, якщо сама ця діяльність викличе в нього інтерес, задоволення, радість, азарт, то можна сподіватися, що в дитини поступово виникне потреба в такій діяльності, а , значить формується стійкий пізнавальний інтерес до неї.

Наприклад, щоби викликати в учнів інтерес до вивчення формул скороченого множення та до їх застосування, організовую                                змагання “Учитель-клас”

       на обчислення значень числових виразів виду 199*201, 252+2*25*5+52, (17+3)(172-17*3+32).

Я виконую обчислення швидко і усно, діти - довго і письмово. Їх зацікавлює ця різниця. У них виникає бажання і самим навчитися так обчислювати, як я.                                                                                                                                                                                                                                                                                    Періодично проводжу математичні диктанти. Вони привчають дітей уважно стежити за мовою вчителя, відразу включатися у виконання завдання, сприяють виробленню певного ритму роботи. Математичні диктанти  застосовую у всіх класах для різних дидактичних цілей, проте є завжди засобом активізації уваги учнів.

Наприклад на уроці геометрії у 7-му класі:

 

Математичний диктант.

Варіант І

1. Закінчіть речення «Сума кутів будь-якого трикутника дорівнює…»
2. Чи існує трикутник з двома прямими кутами?
3. Чи існує трикутник, два кути якого дорівнюють відповідно120 і 80?
4. Один із кутів трикутника тупий. Які два інших кути?
5. Чому дорівнює кут М трикутника МКО, якщо кут К має градусну міру 70 , кут 30? 
6. У трикутнику АВС кут А у два рази більший за кут С, кут В в  три рази більший за кут С. Якого виду трикутник АВС ?     

 Варіант ІІ 

1. Чи існує трикутник, два кути якого дорівнюють відповідно 130 70 ?
2. Чи існує трикутник з двома тупими кутами?
3. Закінчіть речення «Сума кутів будь-якого трикутника дорівнює…2
4. Один із кутів трикутника прямий. Якими є два інші кути?
5. Чому дорівнює кут М трикутника МКО, якщо кут М дорівнює 110 , кут О дорівнює 30 ?
6. У трикутнику АВС кут А на 20 менший від кута В, а кут С на 20 більший за кут В. Якого виду трикутник АВС?                                                                                                                             

Після диктанту  обов’язково робимо корекцію – аналізуємо помилки учнів, спираючись на відповідний навчальний матеріал.

Завжди пам’ятаю, що важливою умовою активізації та підтримування довільної уваги є забезпечення  мотиваційної сторони навчальної діяльності, вироблення позитивного ставлення до того, що пізнається, і до самого процесу пізнання.

Дотримання цієї умови сприяє міцності навичок, що формуються.

З метою активізації уваги часто створюю проблемні та ігрові ситуації тощо.

Знаю, що з метою виховання довільної уваги доцільно застосовувати комп’ютерну програму, яка дає змогу розвантажити вчителя на уроці від другорядних дій, раціональніше спрямувати його зусилля на керування навчальною діяльністю учня, зробити процес сприймання ним, а отже, і засвоєння навчального матеріалу більш ефективним.

Світ змінюється стрімко. Сучасні діти не уявляють свого життя без комп'ютера, хоча використовують його в основному тільки як джерело ігор. Змінюються цілі та завдання сучасної освіти: формування знань і вмінь поступається місцем формування компетентностей. Школи оснащуються комп'ютерною технікою, електронними ресурсами, отримують доступ в Інтернет. Це має сприяти впровадженню в практику роботи сучасних інформаційно-комунікаційних технологій. І все-таки не комп'ютер, а учитель - найбільш важлива складова навчального процесу. Але якщо вчитель не буде розвиватися сам, то є небезпека перетворення комп'ютера в чергове технічний засіб навчання. Компетентностний підхід навряд чи може бути реалізований при традиційних формах і методах навчання. Тільки володіння вчителем сучасними технологіями може сприяти особистісному розвитку учнів.

Основне завдання математики - пошук причинно-наслідкових зв'язків між окремими величинами, тому навчання математики може супроводжуватися організацією проектної та дослідницької діяльності. У цьому випадку комп'ютер - не ТСО і не іграшка, а помічник, що дозволяє зберегти час та сили, джерело нової сучасної інформації. 

Останнім часом значно збільшився випуск програмних засобів, в тому числі і з математики, на CD-дисках. Їх можна умовно розділити на дві групи, що різняться структурою і підходами. Перші - дидактичні ігри, наприклад, "Вчимося вирішувати дробу", "Вчимося вирішувати проблеми", можуть бути використані як на уроках в 5-6 класах, так і в позаурочний діяльності. Веселі анімовані герої, цікава форма подачі матеріалу сприяють безпосередньому запам'ятовуванню і більш якісному засвоєнню знань, дають можливість молодшому підлітку отримати досвід вирішення проблем.  Використання ІКТ в навчанні молодших школярів дозволяє не тільки зробити урок яскравим, нестандартним, але й створює передумови для освоєння способів діяльності.

 Наприклад, найбільше утруднення викликають у школярів 5-6 класів рішення текстових задач. Спільне створення довідника дозволить досягти двох цілей: дати опору учням і отримати досвід систематизації та структуризації матеріалу.  Застосування комп'ютерних технологій навчання в шкільній практиці дає один з шляхів перебудови шкільної освіти.

Відомо, що успішність навчання залежить від відношення дитини до навчання. Позитивне відношення до навчання залежить від мотиву діяльності учня, його інтересу до теми, що вивчається, а також від стійкого інтересу до предмету в цілому. Комп'ютер значно поширив можливості подання навчальної інформації. Застосування кольору, графіки, звуку, сучасних засобів відео техніки дозволяє моделювати різноманітні ситуації і середовища. І це одна з переваг застосування комп'ютерних педагогічних засобів для підвищення інтересу до предмета.

Комп'ютерна підтримка уроків математики в 5-6-их класах, розроблена засобами пакету Power Point. Вона є додатком до уроків, носить навчальний характер і охоплює теми алгебраїчного та геометричного змісту, що вивчаються у 5-6-их класах. Відомо, що основним методом вивчення елементів геометрії в 5-6-их класах є наочно-індуктивний метод. На основі використання цього методу був створений програмний продукт. Він складається зі слайдів і дозволяє подати основні геометричні поняття в цікавій та доступній для школярів формі. У цьому випадку використання комп'ютера з його величезними наочними можливостями є дуже корисним не тільки для школярів, а й для вчителів.

На кожну окрему тему пропонується група слайдів. На першому слайді вказана тема, яка вивчається, наприклад, "Кут", "Коло" і т.д. На наступному слайді школяреві пропонуються завдання, пов'язані з даною темою, і декілька відповідей. Учень може вибрати будь-яку відповідь, яку він вважає правильною. Залежно від того, який варіант відповіді обраний, далі вибирається той чи інший шлях просування школяра у програмі.

На тему "Кут" пропонується група слайдів, створюючи які мали на меті досягти чіткого розуміння учнями таких геометричних понять, як тупий та гострий кути.

Завдання, які пропонуються, мають на меті формування вмінь класифікувати поняття, які задані у графічній формі. Процес виконання завдання такий: розглядаючи кути на екрані, учень знаходить спільні ознаки, потім виключає із запропонованих той кут, який не має спільних ознак з іншими. В залежності від відповіді, програма або пропонує виконати завдання ще раз, або вітає учня і переходить на наступне завдання. Розв'язок подібних задач сприяє формуванню в учнів таких елементів творчої діяльності, як знаходження нової проблеми в знайомій ситуації, визначення структури об'єкту.

Стосовно теми "Многокутник" можна відзначити, що головним у вивченні цієї теми є формування в учнів умінь та навичок розпізнавати види многокутників залежно від кількості їх сторін і кутів.

Школярам можна запропонувати визначити кількість квадратів на малюнку, пропонувати визначити, чим є для прямокутника відрізок. Під час розв'язування таких задач, ми формуємо в учнів здібність до аналітико-синтетичної діяльності, яка знаходить своє виявлення не тільки в умінні відокремлювати елементи того чи іншого об'єкту або поєднувати елементи в єдине ціле, але і в умінні включити його в нові зв'язки, побачити його нові функції.

У наступній темі "Коло" можна досягти чіткого усвідомлення дітьми даної теми і навчити розрізняти всі елементи кола. Школярам  потрібно виявити, чим є для кола даний елемент кола та визначити, чому дорівнює радіус кола, якщо відомий його діаметр. Також можна запропонувати задачу на пошук у рядку фігури, якої бракує. Такі задачі спрямовані на розвиток умінь міркувати послідовно, узагальнювати зображені предмети за ознаками або знаходити відмінності. Учням пропонується розглянути фігури у горизонтальному рядку. З фігур, зображених внизу, потрібно знайти ту, яку треба розташувати зверху на місці фігури, якої бракує. Учні аналізують фігури, які розташовані у горизонтальному рядку, і виявляють закономірності ознак, які повторюються.

Розв'язування таких задач сприяє розвитку в учнів умінь аналізувати, порівнювати, узагальнювати. Опановуючи способи пошуку фігури, якої бракує, діти вже самостійно застосовують їх до розв'язування задач, знаходять свої варіанти розв'язування, виявляючи таку рису творчої діяльності, як альтернативність підходу до розв'язання задач.

      Інформаційні технології відкривають нові можливості в навчанні математики, насамперед це проявляється в тому, що вони стають для учнів засобом пізнавальної діяльності (експериментування з метою перевірки своїх гіпотез, розв’язання задач, порівняння з передбаченнями теорії). Це відповідає головним напрямам оновлення загальноосвітньої школи – діяльнісному підходу, педагогіки співробітництва, які змінюють як роль і місце вчителя в класі, так і характер пізнавальної діяльності учнів.

Педагогічний програмний засіб (ППЗ) «Геометрія, 7 клас» створено згідно з чинною навчальною програмою з математики. Мета ППЗ полягає в активізації пізнавальної діяльності учнів, свідомого засвоєння змісту матеріалу, формування геометричних умінь, просторової уяви, логічного мислення; посиленні пізнавальних і практичних потреб при вивченні геометрії.

Зміст і структуру ППЗ зорієнтовано на розв’язування навчальних завдань через впровадження сучасних педагогічних технологій, у тому числі інтерактивних форм та використання варіативної методики проведення уроків. ППЗ унаочнює як теоретичну, так і практичну частини навчальної програми з геометрії для 7 класу.

Даний ППЗ містить тексти та ілюстрації, відеоматеріали та аудіосупровід, анімаційні фрагменти, завдання для програмованого контролю рівня навчальних досягнень учнів, інтерактивні ресурси тощо.

Разом з цим ППЗ надає можливості для індивідуалізації та диференціації навчання, контролю та самоконтролю рівня навчальних досягнень учнів. Він має інформаційно-довідкову систему для самостійного пошуку учнем необхідної інформації та систему діалогового режиму. Зміст ППЗ узгоджується з підручниками та навчально-методичними посібниками з даного предмета.

Основна мета педагогічного програмного засобу “Бібліотека електронних наочностей “Геометрія, 7-9 класи”– активізувати пізнавальну діяльність учнів, посилити самостійність в опануванні знаннями, вміннями і навичками, мотивацію і інтерес до навчання геометрії і, тим самим, покращити навчальні досягнення учнів.

Одну й ту саму наочність пропонованого ППЗ можна використовувати з різним цільовим призначенням. Залежно від мети і завдань уроку рекомендується використовувати історичні довідки, портрети вчених-математиків, ілюстрації різних практичних ситуацій, які дають змогу обґрунтувати необхідність вивчення того чи іншого геометричного факту.

Актуалізації потрібного для вивчення теми матеріалу сприяє оперативне подання графічно-символьної інформації про раніше вивчені геометричні фігури, операційного змісту потрібних вмінь. Ефективному засвоєнню понять сприяє динамічне унаочнення відповідних геометричних фігур, де виділяються істотні ознаки понять та здійснюється варіація неістотних ознак при збереженні постійними істотних.

Як учитель, що займається навчаючою, виховуючою і розвиваючою діяльністю, намагаюся завжди, коли це можливо, будувати навчально-пізнавальну діяльність учнів за структурою дослідницького методу, за допомогою ППЗ «Геометрія 7-9 класи» починаючи від усвідомлення пізнавальної проблеми і закінчуючи пошуком практичних застосувань одержаних нових знань. Пізнавальні труднощі долаються за допомогою колективного обговорення в класі, спрямованого питаннями, завданнями, коментарями вчителя.

На уроках, де є можливість застосувати мій улюблений дослідницький метод, учні в своїй пізнавальній діяльності за допомогою пакета DG , який є потужним інструментом побудови динамічних геометричних моделей , які називають динамічними рисунками (ДР) проходять такі етапи:

 

1) практична дослідницька робота і висновки про її результати:

2) формування наукового припущення (гіпотези);

3) доведення гіпотези:

4) формування доведеного факту

5) застосування набутих знань у стандартних умовах.

6) застосування набутимх знань у нестандартних умовах.

У здійсненні етапів 1) і 5) приймає участь кожен учень зокрема, а етапи 2), 3), 4) і 6) здійснюються за ініціативою сильніших, кмітливіших учнів.

Дослідницьким методом, наприклад, учні знайомились при вивченні теми «Трикутники» геометрія 7 клас Наприклад:

 

Тема « Перша ознака рівності трикутників»

Завдання

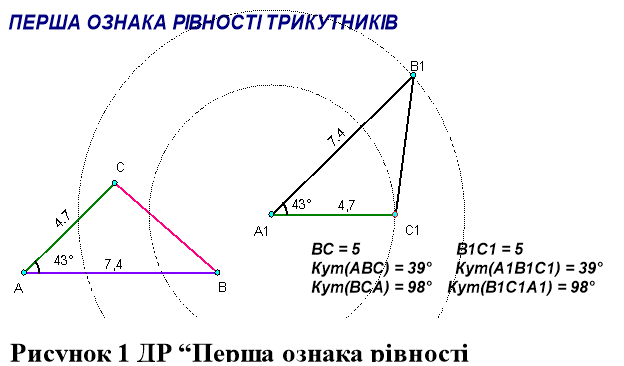Дослідіть за допомогою ДР “Перша ознака рівності трикутників”, чи будуть рівними трикутники ABC і A₁B₁C₁, якщо AB = A₁B₁, AC = A₁C₁, BAC = A₁B₁C₁. (На динамічному рисунку вершини B₁ і C₁ трикутника A₁B₁C₁ лежать на колах з центром A₁, радіуси яких дорівнюють сторонам  AB і AC відповідно. Таким чином, при будь-якому положенні початкових

об’єктів AB = A₁B₁, AC = A₁C₁.)

 

 

Дослідження можна провести за такою схемою:

1. Задайте параметри трикутника ABC, переміщуючи його вершини (при цьому сторони A₁B₁ і A₁C₁ будуть залишатися рівними сторонам AB і AC відповідно).
2. Переміщуючи точку B₁ (або C₁), знайдіть таке її положення, щоб кут A₁B₁C₁ став рівним куту ABC.
3. Порівняйте сторони та кути трикутника ABC з відповідними сторонами та відповідними кутами трикутника A₁B₁C₁ (довжини сторін  BC, B₁C₁ і градусні міри кутів ABC, A₁B₁C₁, BCA і B₁C₁A₁ відображаються на динамічному надписі).
4. Подумайте та перевірте, чи не можуть бути рівними кути A₁B₁C₁ і ABC при іншому положенні точки B₁.
5. Яку гіпотезу можна висунути в результаті ваших спостережень  П ? 
6. Перевірте вашу гіпотезу для трикутника ABC іншої форми та розмірів.
7. Порівняйте вашу гіпотезу з теоремою 3.1 підручника.

Друга ознака рівності трикутників

 

Завдання .1

Дослідіть за допомогою ДР “Друга ознака рівності трикутників”, чи будуть рівними трикутники ABC і A₁B₁C₁, якщо AB = A₁B₁, BAC = B₁A₁C₁, CBA = C₁B₁A₁. (На динамічному рисунку вершина B₁ трикутника A₁B₁C₁ лежать на колі з центром A₁, радіус якого дорівнює стороні  AB. Таким чином, при будь-якому положенні початкових об’єктів AB = A₁B₁. Вершина C₁ лежить на промені A₁D).

Дослідження можна провести за такою схемою:

1. Задайте параметри трикутника ABC, переміщуючи його вершини (при цьому сторони A₁B₁ і AB будуть залишатися рівними).

2. Переміщуючи точку D, знайдіть таке її положення, щоб кут B₁A₁C₁ став рівним куту BAC.

3. Переміщуючи тепер точку C₁ вздовж променя A₁D знайдіть таке її положення, щоб кут C₁B₁A₁став рівним куту CBA.
4. Порівняйте сторони та кути трикутника ABC з відповідними сторонами та відповідними кутами трикутника A₁B₁C₁ (довжини сторін  BC, B₁C₁, AC, A₁C₁  і градусні міри кутів BCA і B₁C₁A₁ відображаються на динамічному надписі).
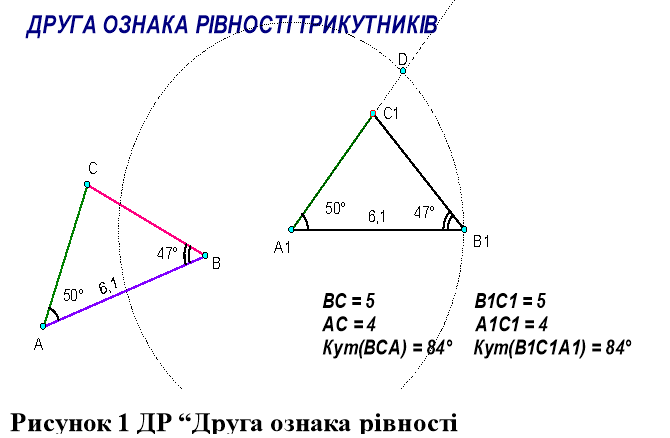5. Подумайте та перевірте, чи не можуть бути рівними кути A₁B₁C₁ і ABC при іншому положенні точки C₁ на промені A₁D.
6. Яку гіпотезу можна висунути в результаті ваших спостережень  П ? 
7. Перевірте вашу гіпотезу для трикутника ABC іншої форми та розмірів.
8. Порівняйте вашу гіпотезу з теоремою 3.2 підручника.

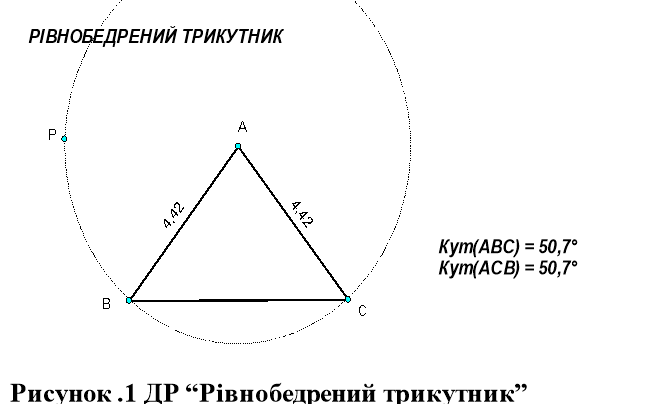
Рівнобедрений трикутник

Трикутник з двома рівними сторонами називається рівнобедреним.

Завдання 1

Дослідіть за допомогою ДР “Рівнобедрений трикутник” властивість кутів при  основі рівнобедреного трикутника. (На динамічному рисунку вершини B і C трикутника ABC лежать на колі з центром A. Таким чином, AB = AC. Переміщуючи точку P або A, ми можемо змінювати радіус кола, а отже, довжину бічної сторони. Переміщуючи точку B або C по колу ми можемо змінювати довжину основи рівнобедреного трикутника ABC.)

ДР “Рівнобедрений трикутник” можна використати для розв’язування рівнобедреного трикутника, тобто для знаходження за деякими заданими елементами трикутника інших його елементів.

 

 

 

Завдання 2

Використовуючи ДР “Рівнобедрений трикутник” розв’яжіть задачі:

9. Дано основу BC і бічну сторону рівнобедреного трикутника ABC. Знайдіть кути трикутника ABC, якщо:
   1. BC = 5, AB = 7;
   2.                    BC = 7, AB = 5;
   3. BC = 5, AC = 5;
   4.                    BC = 7, AC = 7.

2. Дано основу BC і кут при основі рівнобедреного трикутника ABC. Знайдіть два інші кути та бічні сторони трикутника ABC, якщо:
   1. BC = 4,  ABC = 45;
   2.                    BC = 4,  ABC = 60;
   3. BC = 6,  ACB = 30;
   4.                    BC = 8,  ACB = 30.
3. Дано основу BC і кут BAC рівнобедреного трикутника ABC. Знайдіть два інші кути та бічні сторони трикутника ABC, якщо:
   1. BC = 8,   BAC = 90;
   2.                    BC = 12,  BAC = 90;
   3. BC = 9,  BAC = 120;
   4.                    BC = 9,  BAC = 60.
4. Дано бічну сторону і кут при основі рівнобедреного трикутника ABC. Знайдіть основу та два інші кути трикутника ABC, якщо:
   1. AB = 4,  ABC = 45;
   2.                    AB = 10,  ABC = 45;
   3. AC = 6,   ABC = 70;
   4.                    AC = 12,  ACB = 70.
5. Дано бічну сторону і кут при вершині рівнобедреного трикутника ABC.
6. Знайдіть основу та два інші кути трикутника ABC, якщо:
   1. AB = 3,14,  BAC = 120;
   2.                    AB = 8,21,  BAC = 90;
   3. AC = 6,28,  BAC = 60;
   4.                    AC = 12,9,  BAC = 60.     

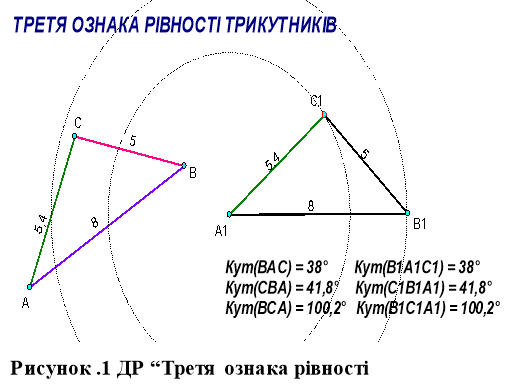
 Третя ознака рівності трикутників

 

Завдання.1

Дослідіть за допомогою ДР “Третя ознака рівності трикутників”, чи будуть рівними трикутники ABC і A₁B₁C₁, якщо AB = A₁B₁, AC = A₁C₁, BC = B₁C₁. (На динамічному рисунку вершини B₁ і C₁ трикутника A₁B₁C₁ лежать на колах з центром A₁, радіуси яких дорівнюють сторонам  AB і AC відповідно. Таким чином, при будь-якому положенні початкових об’єктів AB = A₁B₁, AC = A₁C₁.)

Дослідження можна провести за такою схемою:

10.   Задайте параметри трикутника ABC, переміщуючи його вершини (при цьому сторони A₁B₁ і A₁C₁ будуть залишатися рівними сторонам AB і AC відповідно).
11.   Переміщуючи точку B₁ (або C₁), знайдіть таке її положення, щоб відрізки B₁C₁ і BC стали рівними.
12.   Порівняйте кути трикутника ABC з відповідними кутами трикутника A₁B₁C₁ (градусні міри кутів BCA, CBA, ACB, B₁C₁A₁, C₁B₁A₁ і A₁C₁B₁ відображаються на динамічному надписі).
13.   Перевірте, чи не можуть бути рівними сторони B₁C₁ і BC при іншому положенні точки C₁ на колі (при фіксованому положенні точки B₁).
14.   Яку гіпотезу можна висунути в результаті ваших спостережень  П ? 
15.   Перевірте вашу гіпотезу для трикутника ABC іншої форми та розмірів.
16.   Порівняйте вашу гіпотезу з теоремою 3.6 підручника.

. Корисним тут є і те, що учні, які на кілька хвилин стають дослідниками, мають можливість відчути ту міру людської праці, що була затрачена для добування певних знань. Такі здобуті знання є для них особливо цінними.

На комп'ютерних уроках учні проявили зацікавленість до предмета, добре оволоділи початковими знаннями з геометрії. Процес навчання проходив у невимушеній формі, школярі швидко вирішували поставлені перед ними завдання, не боялися помилитися, були дуже активні, пропонували різноманітні способи розв'язування задач, пробували практично побачити результат. Якщо це не вдавалося, учні шукали нові варіанти, доки не було досягнуто правильного розв'язування задач - все це сприяло формуванню необхідних геометричних понять.

Відзначимо, що застосування даної програми на уроках математики сприяло розвитку пізнавального інтересу учнів, їх розумових здібностей, розвинуло хист до самостійної творчої роботи, що допомагає становленню та розвитку особистості дитини.

 При всіх перевагах дані програмні засоби передбачають наявність у школярів певного досвіду самостійної діяльності. Практика показує, що учневі складно самостійно займатися з диском без спеціальної підготовки. Де цю підготовку отримати? Звичайно, на уроці. Це можливо, якщо вчитель використовує сучасні технології, у тому числі проектну та дослідницьку діяльність. Великі можливості з'являються в старших класах, де математика носить яскраво виражений інтегрований характер. Акцент може бути зроблений на вивчення математичних моделей фізичних, хімічних та інших процесів. Процеси носять динамічний характер, і комп'ютер може бути використаний для проведення навчального експерименту. В якості прикладу наводжу конспекти уроків по темі :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    Алгебра і початки аналізу

                                        Клас: 11

Тема уроку:

"Електронна таблиця Microsoft Excel як засіб дослідження показової функції"

Інтегрований урок інформатика – алгебра і початки аналізу

Клас: 11

Мета уроку: формування умінь застосовувати програмні засоби для дослідження математичних функцій

Завдання:

Побудувати математичну модель "закону органічного зростання";

Досліджувати математичну модель за допомогою програми Microsoft Excel;

Отримати математичну запис "закону органічного зростання".

 

Обладнання: мультимедійний проектор, мультимедійна презентація у програмі Microsoft Power Point, відеофрагмент фільму "Епідемія", роздавальний матеріал, комп'ютерний клас.

 

 

 

 

Хід уроку

Мотивація

З самого народження людина повинна вирішувати якісь проблеми. Перед людством стоять і глобальні проблеми. Про одну з них піде мова на уроці. Демонструється презентація (зміст презентації в кінці конспекту). Здається, що все це було давно і з нами такого не станеться. / Демонструється фрагмент фільму "Епідемія". / Новий вік зустрів нас новими хворобами, які забирають життя багатьох і багатьох людей. Причина епідемій - велика швидкість розмноження вірусів. Звичайно, проблему епідемій на уроці ми не вирішимо, але ми зможемо встановити, на скільки швидко розмножуються віруси, і отримати математичну запис "закону органічного зростання", важливого для вирішення проблеми епідемій.

Постановка навчальної задачі

В результаті наукових досліджень встановлено, що швидкість зростання чисельності живих організмів пропорційна їх чисельності. Знайти "закону органічного зростання".

Створення математичної моделі                                                                                                

Аналіз навчального завдання: виділити основні поняття в задачі; назвати відповідні математичні поняття; записати їх символічно. В результаті з'являється таблиця. Основні елементи завдання              

Математичні поняття  Символічний запис

Чисельність живих організмів

Швидкість їхнього росту

Пропорційність чисельності та швидкості  Залежна мінлива

Похідна

Відношення величин є постійна величина  

Закон органічного росту  Знайти функцію  

У результаті аналізу отримана математична задача:

Дано:

Знайти:  .

Отримано рівняння нового вигляду. Рівняння, що зв'язує невідому функцію і її похідну, називається диференційних.

Іноді спочатку вирішують приватну задачу. Нехай K = 1, тоді задача прийме вигляд:

Дано:

Знайти:  .

Рішення математичної задачі

Переформулюємо задачу: функція та її похідна збігаються або збігаються їх графіки. Серед відомих похідних функцій такої немає. Гіпотеза - чи може показова функція бути рішенням диференціального рівняння? Спочатку згадаємо, що ми знаємо про цю функцію.

Картка для повторення

Заповни пропуски:

а) Функція, задана формулою , де __________, називається _______. D (y )=_____, E (y )=____.

 

б) Графік цієї функції має вигляд:

при 0 <A <1 при A> 0

в) Невідома похідна показової функції. Скористаємося визначенням похідної.

 Уточни проблему: при якому значенні A графіки функцій  і  збігаються?

Комп'ютерний експеримент

Побудувати графіки вказаних функцій при різних значеннях A у програмі Microsoft Excel; підібрати число, при якому графіки практично збігаються. У результаті експерименту отримали. У більш глибоких дослідженнях з'ясували, що це число ірраціональне. Дали спеціальну назву e. Функцію  назвали експонентів.

Результат

Яке відношення Лев Толстой має до числа E?

 "Спосіб запам'ятати E простий: два, сім і двічі Лев Толстой". Ввести в комірку число E, перевірити збіг графіків.

Таким чином, отримали  . В результаті більш глибоких досліджень отримали математичну запис "закону органічного росту"  .

 

Швидкість розмноження вірусів дійсно дуже велика. Розрахуйте кількість вірусів через 10 сек, 1хв, 1час з початку їхнього розмноження в організмі.

Підсумок.

По "закону органічного росту" змінюється не тільки кількість живих організмів, але й населення країни. По "закону органічного убування" відбувається радіоактивний розпад, змінюється тиск повітря з висотою і т. д.

 

Такі різні процеси описані однією моделлю. Це використовується в науці - якщо не можна реально провести експеримент, розглядають подібний процес.

 

Домашнє завдання

Скласти план докази диференціювання показової функції і за бажанням знайти інші подібні процеси.

Зміст презентації для початку уроку

У літописі середніх віків описані страшні картини існування  чуми. У XVI столітті за 50 років чума забрала життя 100млн. чоловік. У XVI столітті в Європі загинула від чуми чверть населення. Від віспи загинуло ще більше людей. У XVI столітті щорічно від віспи вмирало 400 тисяч чоловік. У XVI столітті стала поширюватися холера. У Росії до 1917 року за 59 "холерного" лет занедужало 5,9 млн. чоловік, майже половина з них загинула. Епідемія грипу вбила в 1918 році понад 20 млн. землян. XXI століття - нові епідемії. Як з ними боротися?

 

При всьому багатстві програмних засобів не всі теми курсу математики в них охоплені, та й творчо думаючому учителю рамки запропонованих курсів бувають тісні. Освоєння вчителем комп'ютерної техніки як користувачем дозволяє розширити можливості застосування комп'ютера на уроках математики. Мультимедійні презентації, створені у програмі Power Point (передбачається, що комп'ютер оснащений системою Microsoft Office) можуть супроводжувати весь урок або бути його частиною, можуть бути продуктом проектної, дослідницької діяльності. Наприклад, на тему "Правильні багатогранники" відводиться 1 година, а матеріал дає можливість познайомитися не тільки з історією розвитку математики, але і з деякими науковими гіпотези. Проект з даної теми сприяє підтримці інтересу до математики і дає можливість попрацювати з іншими, крім підручника, джерелами.

 

 

 

 

               Алгебра і початки аналізу

                                Клас: 11

Тема уроку:

"Дослідження функції за графіком похідної"

 

Мета уроку: формування вмінь досліджувати функції за графіком похідної

Завдання:

навчити читати графік похідної функції;

дати можливість учням отримати досвід пере формулювання завдань, відомості їх до стандартних завдань;

Обладнання: мультимедійний проектор, мультимедійна презентація у програмі Microsoft Power Point, роздавальний матеріал.

 

 

Хід уроку

Мотивація

Як може бути задана функція?

Як може бути задана похідна функції?

Демонструється завдання. Проаналізуємо задачу. Що дано? Що потрібно знайти? Як вирішити задачу?

 

Узагальнимо задачу: за графіком похідної отримати інформацію про властивості функції.

 

Повідомляється тема уроку. Ставляться завдання - навчитися читати графік похідної функції і отримати досвід пере формулювання завдання, відомості її до стандартної.

 

Актуалізація

 

Який теоретичний матеріал допомагає в дослідженні функції?

Учні формулюють визначення критичної точки, необхідна умова екстремуму, достатні умови екстремуму і зростання, спадання функції.

Що ми вміємо знаходити за графіком похідної?

На попередньому уроці діти навчилися за графіком похідної знаходити нулі похідної і визначати її знаки. Для повторення учні індивідуально заповнюють картку з подібними завданнями. Фронтальна перевірка. Зворотній зв'язок.

 

Узагальнення знань, отримання опори.

Працюють в парах, вставляють пропущені слова в пропозиції:

 

В точці X 0 похідна дорівнює 0, отже X 0 - ____________________________

На проміжку (A; B) похідна позитивна, отже функція ___________________

На проміжку (A; B) похідна негативна, отже функція ____________________

В точці X 0 похідна змінює знак, отже X 0 - __________________________________

 

В точці X 0 похідна змінює знак з "+" на "-", отже X 0 - ________________________

 

В точці X 0 похідна змінює знак з "-" на "+", отже X 0 - ________________________

 

Перевірка.

Закріплення умінь читати графік

Спираючись на пропозиції, отримані в парній роботі, читають графіки похідної, запропоновані вчителем.

Наприклад, за графіком / ріс1 / знаходимо нуль похідної X = 2, визначаємо знаки похідної: на проміжку  похідна негативна, на проміжку  похідна позитивна. Отже, на проміжку  функція зменшується, а на проміжку  функція зростає. В точці X = 2 похідна змінює знак з - на +, отже 2 - точка мінімуму.

Зручно міркування супроводжувати їх фіксацією рис. 1

на числової осі. - 2 +

Потім читають графік .З'ясовують, що для вирішення завдання цієї інформації недостатньо. Повторяємо геометричний зміст похідної. Рішення задачі. Творче завдання: придумати до графіку демоверсії нове запитання. Учні працюють у четвірку.

 

Контроль

Вибрати з трьох запропонованих завдань найбільш цікаву і вирішити. Фронтальна перевірка

 

Дача домашнього завдання

Вирішити решту завдання.

Рефлексія

Вирішено Чи поставлені завдання? Що ще треба зробити?

Усі дидактичні матеріали демонструються і на екрані.

Безсумнівно, комп'ютер на уроці математики не данина моді. Він робить викладання динамічним, дозволяє реалізувати сучасні особистісно-орієнтовані технології. Вчителю потрібно лише бути відкритим до всього нового, постійно підвищувати свій професійний рівень. А також не варто боятися, що сучасні діти розбираються в техніці краще за нас, навпаки це дозволить втілити в життя технологію співпраці.

 

 

   математика

                                                           5-й клас

Тема уроку:

"РОЗВ’ЯЗУВАННЯ ВПРАВ НА ВСІ ДІЇ З ДЕСЯТКОВИМИ ДРОБАМИ."    

Мета: узагальнити і систематизувати знання учнів з теми; закріпити навички учнів виконувати всі дії над десятковими дробами; розвивати логічне мислення, увагу, інтерес до предмета; формувати навички самоконтролю; виховувати активність.

 

Обладнання: індивідуальні завдання, завдання для груп, фішки.

 

Якщо не висловлено різних думок,

                                                    немає з чого вибрати краще.

Хід уроку

І. Мотивація (до виконання всіх дій над десятковими дробами)

1. Бесіда вчителя з учнями

 

• Чи все ви знаєте про десяткові дроби та дії над ними?

• Чи треба людям уміти виконувати такі дії?

 

2. Оголошення теми і очікуваних результатів

3. Інтерактивна вправа „Мікрофон”

Учитель пропонує відповісти на запитання (за кожну правильну відповідь учень отримує фішку зеленого кольору – 1 бал).

1) Сформулюйте правило віднімання десяткових дробів.

2) Сформулюйте правило віднімання десяткових дробів.

3) Сформулюйте правило множення десяткових дробів.

4) Сформулюйте правло ділення десяткових дробів.

5) Як знайти невідомі:

• доданок;

• зменшуване;

• від’ємник;

• множник;

• ділене, дільник.

 

ІІ. Узагальнення, систематизація і корекція знань, вмінь і навичок учнів

4. Учитель пропонує учням виконати усно вправи (кожна правильна відповідь – фішка – 1 бал):

1) 2,8 + 0,2 

а) 2,82 

б) 3 

в) 2,28 

г) 2,1

2) 3,84 – 2,8 

а) 1,04 

б) 1,4 

в) 1,6 

г) 1,2

3) 25 * 0,4 

а) 1 

б) 0,01 

в) 10 

г) 0,1

4) 0,55 : 0,5 

а) 1,1 

б) 1,01 

в) 0,11 

г) 11

5) 10,2 : 0,1 

а) 1,002 

б) 1,02 

в) 0,102 

г) 102

Підводиться підсумок.

5. Робота в групах

Учням необхідно виконати приклади (відгадавши при цьому зашифроване слово або число) – фішка – 3 бали (червона).

 

Перша група (2,18 + 10,82) * 0,12 – 0,28.

Друга група (41 – 23,4) : 0,4 + 0,25 * 0,84

Третя група (171,9 – 147,4) : 0,05 + 0,48 * 0,16

Завдання учні виконують у зошитах.

6. Вправа „Мозковий штурм”

Учитель пропонує розв’язати задачу. Той учень, який висловлює правильні пропозиції, отримує фішку (1 бал).

Задача.

До свого дня народження Буратіно купив 12 кг шоколадних цукерок по 3,4 сольдо за кілограм, 7,5 кг зефіру по 2,6 сольдо за кілограм і 14 пляшок лимонаду по 1,5 сольдо за пляшку. Скільки грошей залишилось у Буратіно, якщо спочатку в нього було 100 сольдо?

7. Робота в групах (однорівневі)

Перша група х * 12 = 112,8

Друга група 2,7х – 1,3х + 3,6х = 2

Третя група 9,66 : (х + 0,17) = 23

Кожна група робить презентацію розв’язку свого рівняння.

Вправа „Презентація”.

ІІІ. Підсумок уроку

„Рефлексія”.

Девіз: „Кажи не чого вчишся, а чого пізнав?”

Учні відповідають на запитання вчителя:

• Що цікавого було на уроці?

• Що сподобалось найбільше?

V. Консультант кожної групи підводить підсумки роботи кожного учня.

Учитель виставляє оцінки.

VI. Подача домашнього завдання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Геометрія 7 клас

Тема: Суміжні та вертикальні кути

Мета: домогтися свідомого розуміння учнями означення суміжних і                            вертикальних кутів, сформулювати в учнів уміння розпізнавати на готовому рисунку пари суміжни і вертикальних кутів, будувати кути в динамічному рисунку (ДР)

Навчальна мета:

Провести дослідження властивостей суміжних та вертикальних кутів.

Тип уроку: засвоєння нових знань  (навчальне дослідження)

Конструкторська діяльність

Для проведення конструкторської діяльності ви повинні знати означення суміжних та вертикальних кутів.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

ІІІ. Мотивація навчальної діяльності учнів.

      Для створення позитивної навчальної діяльності учнів проводимо дослідження на комп’ютері розв’язуючи такі завдання:

1.Побудуйте три довільні точки А, В, С так, щоб вони не лежали на одній прямій (використайте інструмент Точка)

2.Побудуйте промінь СА (використайте інструмент Промінь)

3.Побудуйте промінь СB .

4.Виміряйте кут АСВ . Запишіть його градусну міру: ________

5.Одержаний результат порівняйте з наведеним на рис.2.1.

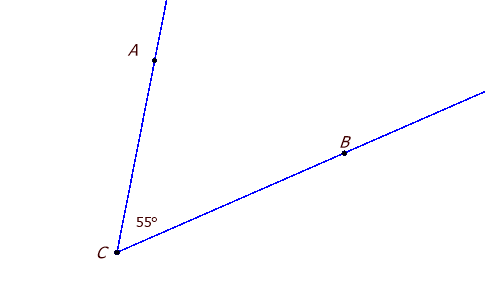Рис. 2. 1

 

 

 

 

 

 

 

 

 

 

 

6.Динамічно змініть положення точки А (або В, С) та, спостерігаючи за зміною градусної міри кута, зробіть так щоб кут АСВ став:

Рис. 2. 2

1. прямим    АСВ  = ______
2. гострим: ­­­_______ < АСВ < _______
3. тупим:   _______ < АСВ <
4. розгорнутим:  АСВ  = ______      

ІY. Формулювання мети і завдань уроку

7.Побудуйте промінь СD (використайте інструмент Промінь)

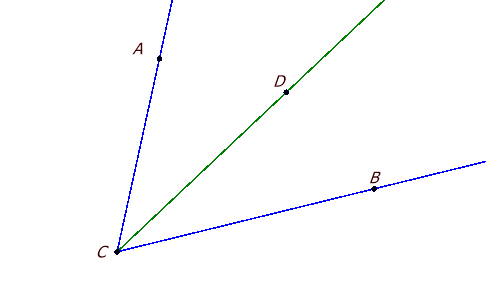
8.Динамічно змініть положення точки А (або В, або С чи D) так, щоб кути ACD та DCB стали суміжними. Проведіть пряму CB та прив’яжіть точку А до неї (команда Пристебнути до фігуриПряма1 рис. 2.4). Динамічно змініть положення точки А. Дослідіть, як вона може переміщуватися: ______________________________________

Рис. 2. 3

9.Вставте пропущені назви сторін кутів у речення:

Кути ACD та DCB – суміжні, якщо ______ спільна сторона кутів, а сторони _____ та _____ є додатковими півпрямими.

 

10.Виміряйте кути , динамічно змініть положення точок В, C, D, та запишіть декілька варіантів вимірювання:

11.

5. ACD = ______, DCB = ________, АСВ = _______
6. ACD = ______, DCB = ________, АСВ = _______
7. ACD = ______, DCB = ________, АСВ = _______

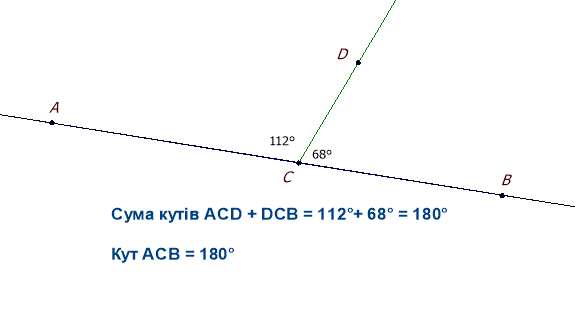
12.Обчисліть суму кутів ACD + DCB та градусну міру кута АСВ: використайте команду Добавити надпис та запишіть в вікні діалогу, застосовуючи, для зручності, калькулятор:

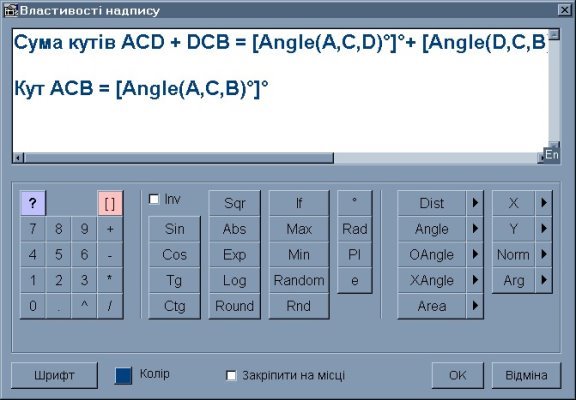
Рис. 2. 4

13.Динамічно змініть положення точок B, C, D. Дослідіть зміни у формулі.

14.Відв’яжіть точку А від прямої (команда Відв’язати точку) та динамічно змініть положення точок B, C, D. Зверніть увагу на зміни у формулі. Знову прив’яжіть точку А  до прямої (див. пункт 8).

Рис. 2. 5 ДК 2. 1

15.Зробіть висновок:

Сума суміжних кутів дорівнює __________

16.Побудуйте промінь СЕ (використайте інструмент Промінь)

17.Виміряйте кути ACE і DCB :

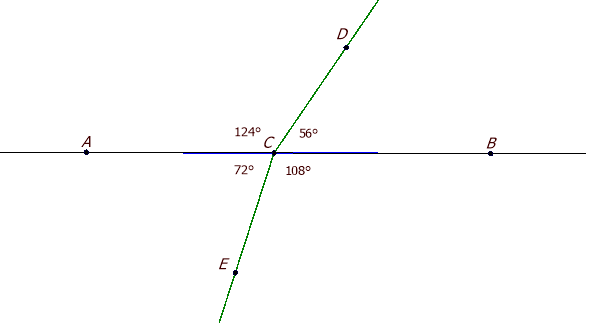
Рис. 2. 6

18.Динамічно змініть положення точки А (або В, або С чи D) так, щоб кути ACЕ та DCB стали вертикальними. Проведіть пряму CВ та прив’яжіть точку E до неї (команда Прив’язати до фігуриПряма2  рис.2.6.).

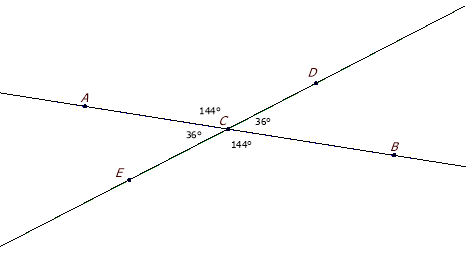
Рис. 2. 7

19.Вставте пропущені назви сторін кутів у речення:

Кути ACE та DCB – вертикальні, якщо сторони другого кута _____ i  _____ є додатковими півпрямими сторін _____ i  _____ першого кута.

20.Змініть положення точок В, C, D, та запишіть декілька варіантів вимірювання:

8. ACЕ = ______, DCB = ________
9. ACЕ = ______, DCB = ________
10. ACЕ = ______, DCB = ________

21.Зробіть висновок:

Вертикальні кути ______________

Y. Засвоєння нових знань

Завдання

1. Побудуйте бісектриси  суміжних кутів  ACD і DCB (використайте інструмент Бісектриса) та дослідіть, який кут утворюється між бісектрисами суміжних кутів.
2. Побудуйте бісектриси вертикальних кутів  ACЕ і DCB  та дослідіть їх властивість.

Письмові завдання

1.Кути 1 і 2 та кути 3 і 4 – дві пари суміжних кутів.

Порівняйте кути 2 і 4, якщо кут 1 більший за кут 3.

2.Визначте вид двох кутів, що утворилися при перетині двох прямих, якщо:

а) один із них на 20 більший за інший;

б) їх сума дорівнює 120 .

YІ . Підсумки уроку

1. Два кути мають спільну сторону. Чи означає що ці кути:
2. а) мають спільну вершину
3. б) ці кути є суміжними.
4. в) їх сума дорівнює 180 ?
5. Чи можуть дві прямі, перетинаючись, утворювати три гострі кути; тільки один тупий кут; чотири прямі кути?

YІІ. Домашнє завдання

 

Знайти:

а) кут ВОС, якщо   ВОД=112,     АОС=138

Вивчити    п. 4.; 5    № 10

ЛІТЕРАТУРА

 

1.л.с. Виговський, Розумовий розвиток дітей в процесі навчання.

М.1995.

2.О.І.Пометун, Л.В. Тироженко. Сучасний урок.

К.Видавництво А.С.К.2004.

3. М.І.Жалдак, О.В. Вітюк . Комп’ютер на уроках геометрії.

К.2004.

4.В.Я.Романюк, Л.І.Дутко. Технології інтерактивного навчання на уроках математики. Львів, Тріада плюс, 2004.

 

 

 

 

 

 

 

 

 

 

 

 

 

                                      

 

                            З М І С Т

                                                                                                   ст.

1.Вступ.                                                                           2

2.Способи активізації навчально–пізнавальної     3    діяльності на уроках математики.

               2.1.Мотивація навчання.                              4

               2.2. Актуалізація опорних знань.                6

               2.3. Інформаційні технології.                       8

3.Висновки.                                                                   17

4.Додатки.                                                                      18

5.Література                                                                  34