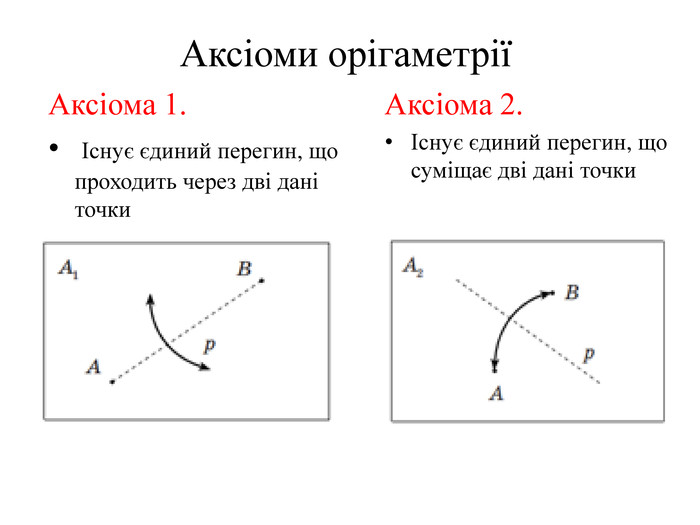
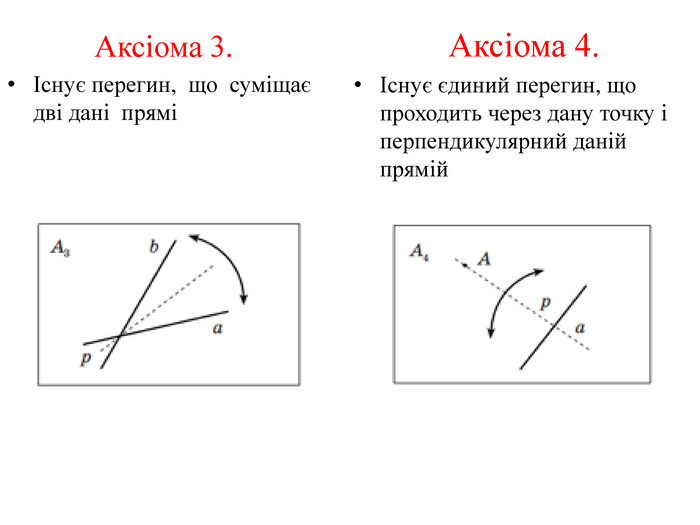
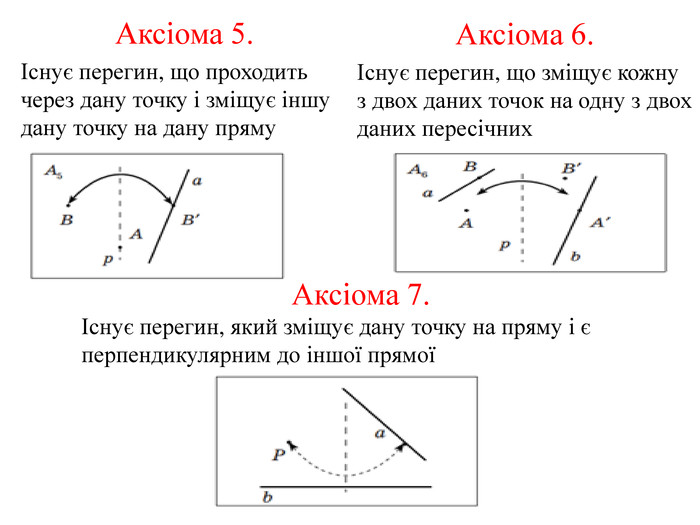
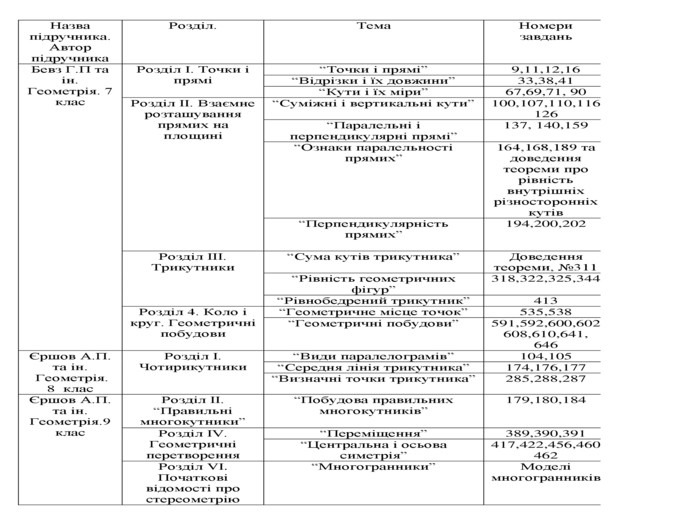
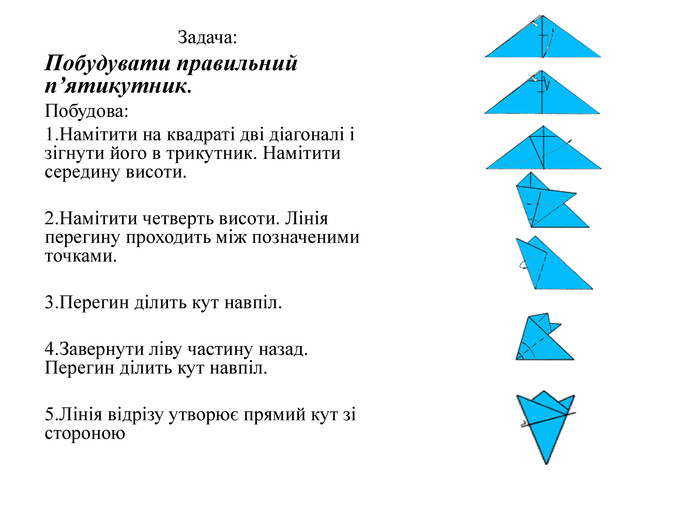
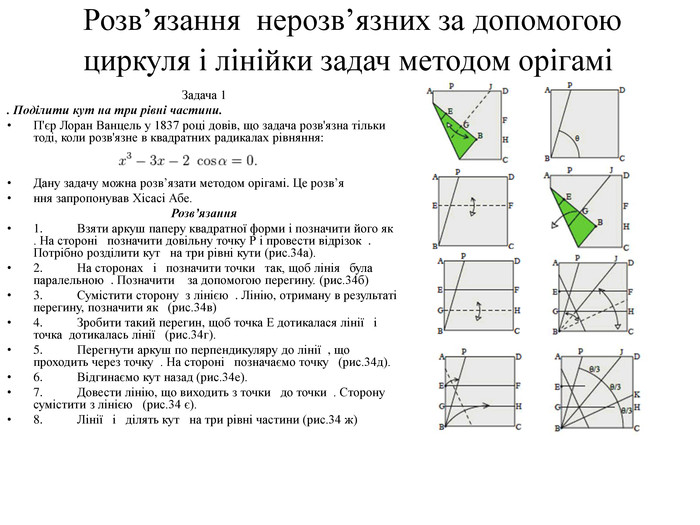
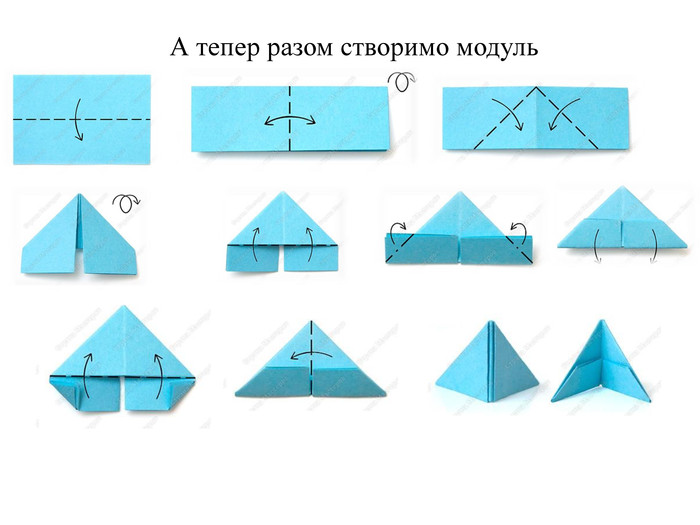
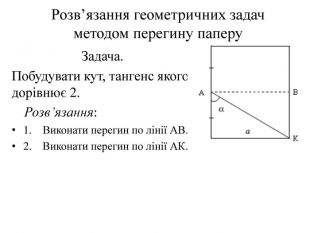
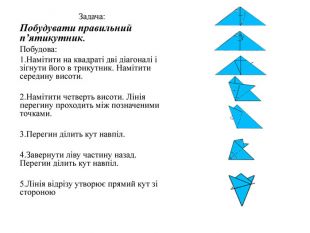
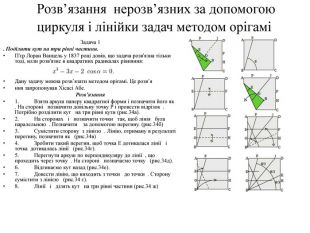
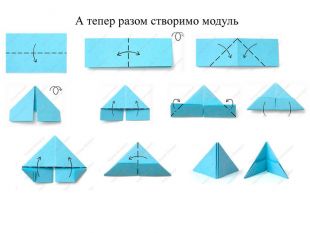
Математика в оригамі
Про матеріал
Структурована інформація про задачі, які вирішуються шляхом оригамі. Дітям буде дуже цікаво, особливо, якщо робити фігурки разом з ними за допомогою модульного оригамі. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Досить цікаво і повчально!


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку