Новий спосіб розв'язування задач при змішуванні речовин - правило "коромисло Івашини".

Порада. Щоб повноцінно ознайомитись з новим способом розв’язування задач – завантажте файл з роботою, бо на сторінці сайту не відтворюються більшість графічних зображень та зрозуміти сутність нового способу неможливо.

В наш час, час швидких технологічних змін дуже поважають та цінують людей, які можуть вирішити проблему, використовуючи різні способи, які здатні в складній ситуації оцінити широко, масштабно задачу та розв’язати її.

В своїй роботі, як вчитель, я завжди націлюю дітей на те, що кожну справу треба доводити до кінця; кожне завдання треба виконувати вірно; із усіх варіантів вирішення проблеми використовувати найкоротший та найпростіший спосіб.

Хімія – це цікава, але не проста наука, з нею можуть потоваришувати не всі люди. Та в мене є мета – зробити так, щоб хімія була зрозумілою більшій кількості людей, ніж зараз.

При розв’язуванні задач завжди є декілька варіантів, щоб знайти рішення. Способи ров’язку не завжди є простими і зрозумілими.

В цій  роботі я хочу всім запропонувати спосіб розв’язування задач пов’язанних з приготуванням розчинів та сплавів з певною масовою часткою розчиненої речовини або металу, зі знаходженням складу сплавів та газових сумішів використовуючи правило, яке назвав «коромисло Івашини». Для цього розв’яжемо декілька задач, використовуючи відомі раніше (стандартні) способи та правило, що було вказано вище. Але спочатку вкажемо величини, що будуть використовуватись при розв’язанні.

m₁ – маса розчину з меншою концентрацією, що буде змішуватись або це може бути маса води, якщо її використовують для приготування нового розчину.

w₁% – масова частка розчиненої речовини у розчині з меншою концентрацією (якщо m₁ – це маса води, то w₁%(р.р.) = 0%).

m₂ – маса розчину з більшою концентрацією, що буде змішуватись або це може бути маса розчиненої речовини, якщо її використовують для підвищення концентрації нового розчину.

w₂% – масова  частка розчиненої речовини у розчині з більшою концентрацією (якщо m₂ – це маса розчиненої речовини, що використовують для підвищення концентрації, то w₂%(р.р.) = 100%).

m₃ – маса утвореного розчину.

w₃% – масова частка розчиненої речовини в утвореному розчині.

А зараз давайте розглянемо алгоритм використання правила «коромисло Івашини»:

1. Будуємо відрізок на якому вказуємо масові частки розчинених речовин обох розчинів, що змішуються:

 

2. В середній частині відрізку вказуємо значення масової частки утвореного розчину:
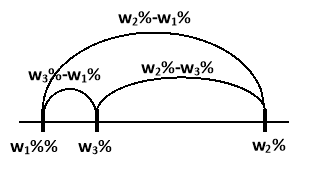3. Визначаємо довжини трьох відрізків:
4. Маси змішуваних розчинів знаходимо за формулами:

 

Задача №1

За одним з рецептів для приготування смачної страви з м’яса необхідно до 1 кг м’яса додати 150 г розчину оцтової кислоти з масовою часткою 18%. Приготуйте необхідну кількість потрібного розчину для замочування 5 кг м’яса. Для цього можна використовувати розчини оцтової кислоти з концентрацією 9% та 60%.

Розв’язання

Спосіб №1 (стандартний)

Як зрозуміло з умови задачі необхідно приготувати 5×150 г = 750 г розчину з масовою часткою оцтової кислоти 18%. Позначемо масу цього розчину - m₃.

Наше завдання визначити маси розчинів з масовими частками оцтової кислоти 9% та 60%, що необхідно взяти для приготування розчину m₃. Позначимо відповідно їх маси m₁ та m₂. Надамо значення розчинам m₁ та m₂: m₁ = x, m₂ = y.

Враховуючи це запишемо:

m₁ + m₂ = m₃, або x + y = 750.

Знаходимо масу оцтової кислоти, що міститься в третьому розчині:

m₃(CH₃COOH) = w₃(CH₃COOH)×m₃ = 0,18×750 = 135 (г)

Відповідно знайдемо маси оцтової кислоти, що містяться в першому та другому розчині:

m₁(CH₃COOH) = w₁(CH₃COOH)×m₁ = 0,09x

m₂(CH₃COOH) = w₂(CH₃COOH)×m₂ = 0,6y

Оскільки

m₁(CH₃COOH) + m₂(CH₃COOH) = m₃(CH₃COOH), то

0,09x + 0,6y = 135

Таким чином можна скласти систему рівнянь з двома невідомими:

x + y = 750

0,09x + 0,6y = 135;

Розв’яжемо її:

x = 750 – y

0,09 (750 - y)+ 0,6y = 135;

0,09 (750 - y)+ 0,6y = 135

67,5 – 0,09y + 0,6y = 135

0,51y = 67,5

y = 132,35

x = 750 – y = 750 – 132,35 = 617,65

Отже m₁ = 617,65 г, m₂ = 132,35 г.

Спосіб №2

При розв’язанні задачі використаємо спосіб «квадрат Пірсона» (правило хреста). Пригадаємо гафічну модель вказаного способу та формулу для розрахунку:

Щоб скористатись правилом хреста величинам m₁ та m₂ надамо значення m₁ = x, а m₂ = 750 - x.

 

Підставляємо значення у формулу

Отже m₁ = 617,65 г, а m₂ = 750 – 617,65 = 132,35 г.

 

 

Спосіб №3

Скористаємось правилом «коромисло Івашини». Знаходимо величини за вказаним вище алгоритмом. Для цього зобразимо відрізок в якому початковим значенням буде масова частка оцтової кислоти розчину з меншою концентрацією, а кінцевим – масова частка оцтової кислоти розчину з більшою концентрацією:

 

 

 

Між цими значеннями вкажемо масову частку оцтової кислоти утвореного розчину:

 

 

 

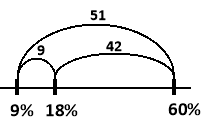Вкажемо довжини утворенних відрізків:

Таким чином вклад першого розчину в утворення третього складає частин, а вклад другого розчину -  частин, тому

Перевага способу №3 полягає в тому, що для розв’язання задачі не треба вводити ніяких змінних, не треба проводити досить складних арифметичних розрахунків в яких діти часто роблять помилки, а також графічна модель «коромисла Івашини» набагато простіша та зрозуміліша, ніж при використанні «квадрату Пірсона».

Задача №2

Яку масу води та розчину натрій хлориду (NaCl) з масовою часткою 30% необхідно взяти для приготування 400 г розчину натрій хлориду з масовою часткою 12%?

Розв’язання

Задачу розв’язуємо використовуючи правило «коромисло Івашини».

m₁ – маса води

m₂ – маса розчину з концентрацією 30%

m₃ – маса розчину, що необхідно приготувати

Врахуємо, що у чистій воді масова частка розчиненої речовини становить 0%.

Складаємо відрізки та знаходимо їх довжини:

 

 

 

 

 

 

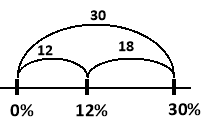
Відповідь: m₁ = 240 г, m₂ = 160 г.

Задача №3

Яку масу розчину калій нітрату з масовою часткою 25% та сухої солі калій нітрату необхідно взяти для приготування 500г розчину з масовою часткою калій нітрату 42%?

Розв’язання

– маса розчину з концентрацією 25%

– маса сухого KNO₃, що необхідно додатково розчинити

– маса розчину з концентрацією 42%

Врахуємо, що в сухій солі масова частка розчиненої речовини 100%

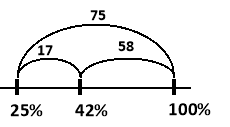Будуємо відрізки та знаходимо їх довжини:

Відповідь: m₁ = 386,67 г, m₂ = 113,33 г.

Задача №4

Скільки сухої солі необхідно дадати до 200 г розчину з масовою часткою солі 15% для підвищення концентрації до 30%?

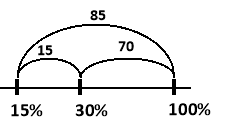Розв’язання

 звідси слідує, що

 

 

Відповідь:

«Коромисло Івашини» також можна використовувати для виконання розрахунків при розчиненні у воді або у розчинах кристалогідратів. Вказаний спосіб дуже спрощує розрахунки. Кристалогідрати – це сухі на дотик речовини, що у своєму складі містять воду, тому до них можна також  відноситись як до розчинів.

Задача №5

Яку масу розчину купрум (ІІ) сульфату (CuSO₄) з масовою часткою 20% та мідного купоросу (CuSO₄5H₂O) необхідо взяти для приготування 400 г розчину купрум (ІІ) сульфату (CuSO₄) з масовою часткою розчиненої речовини 36%?

Розв’язання

Спочатку необхідно знайти масову частку купрум (ІІ) сульфату в мідному купоросі:

Mr(CuSO₄5H₂O) = Mr(CuSO₄) + 5Mr(H₂O) = 160 + 5×18 = 250

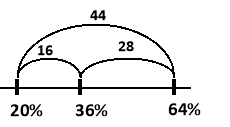
Далі використовуємо правило «коромисло Івашини»:

 

 

 

Відповідь: m₁ = 254,55 г, m₂ = 145,45 г.

Задача №6

Які маси води та залізного купоросу слід узяти для приготування  300г розчину ферум (II) сульфату (FeSO₄) з масовою часткою розчиненої речовини 25%?

Розв’язання

Знаходимо масову частку FeSO₄  в залізному купоросі:

Mr(FeSO₄ 7H₂O) = Mr(FeSO₄)+7Mr(H₂O) = 152+7×18 = 278

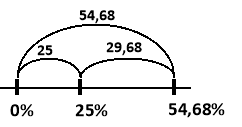
(г)

 

Таким чином необхідно взяти 162,84 г води та 137,16 г залізного купоросу.

Задача №7

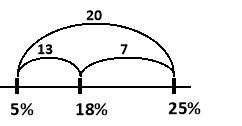Один вид сталі містить 5% нікелю, другий – 25%. Скільки сталі кожного виду треба взяти для одержання 60 т сталі, що містить 18% нікелю? Розв’язання

Таким чином необхідно взяти 21 т сталі з масовою часткою нікелю 5% та 39 т сталі з масовою часткою нікелю 25%.

Задача №8

В хімічну лабораторію для аналізу принесли зразок сплаву золота та міді масою 300 г. Мета аналізу – визначити маси металів у сплаві. Лаборант,  використовуючи мірний циліндр з водою, визначив об’єм шматка сплаву – 24 мл. Допоможіть визначити маси золота та міді якщо (Au) = 19,3 г/мл, а (Cu) = 8,96 г/мл.

Розв’язання

Щоб використовувати правило «коромисло Івашини» для розв’язання задач даного типу необхідно в алгоритм розв’язку внести деякі зміни, а саме:

1. Будуємо відрізок на якому вказуємо значення густин обох металів, що входять до складу сплаву (₁ – густина металу значення якої менше, ₂ – густина металу значення якої більше):

2. В середній частині відрізку вказуємо значення густини сплаву (₃):
3. Визначаємо довжини трьох відрізків:
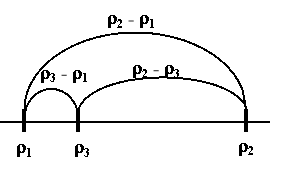4. Знаходимо об’єми металів, що входять до сплаву за формулами:

 

Спочатку знаходимо густину сплаву:

₃(сплаву) = m₃(сплаву)/V₃(сплаву) = 300/24 = 12,5 г/мл

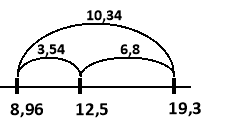Будуємо відрізки на яких вказуємо значення густин (по краям густини металів, всередині – густина сплаву) та знаходимо їх довжини:

Знаходимо об’єми металів:

, а потім маси металів:

m₁ (Cu) = (Cu)×V₁(Cu) = 8,96×15,78 = 141,4 (г)

m₂ (Au) = (Au)×V₂(Au) = 19,3×8,22 = 158,6 (г)

Задача №9

Чи дійсно шматок латуні масою 200 г та об’ємом 23,465 см³ можна віднести до латуні з маркуванням Л80? ((Zn) = 7,133 г/см³, (Cu) = 8,96 г/см³)

Розв’язання

Спочатку знаходимо густину сплаву:

₃(сплаву) = m₃(сплаву)/V₃(сплаву) = 200/23,465 = 8,523 г/мл

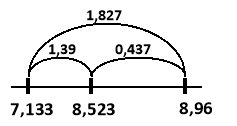Будуємо відрізки на яких вказуємо значення густин (по краям густини металів, всередині – густина сплаву) та знаходимо їх довжини:

Знаходимо об’єми металів:

, а потім маси металів:

m₁ () = (Zu)×V₁(Zu) =7.133× 5.613= 40 (г)

m₂ () = (Cu)×V₂(Cu) = 8,96×17.852= 160 (г)

,

Латунь з маркуванням Л80 якраз і містить 20% цинку та 80% міді.

Задача №10

Середня відносна молекулярна маса газової суміші метану (CH₄) та вуглекислого газу (CO₂) – 24. Який обєм метану та вуглекислого газу міститься в 30 літрах такої суміші?

Розв’язання

Щоб використовувати правило «коромисло Івашини» для розв’язання задач даного типу необхідно в алгоритм розв’язку внести деякі зміни, а саме:

1. Будуємо відрізок на якому вказуємо значення відносних молекулярних мас газів, що входять до складу суміші (Mr₁ – відносна молекулярна маса значення якої менше, Mr₂ – відносна молекулярна маса значення якої більше):
2. В середній частині відрізку вказуємо значення відносної молекулярної маси суміші газів (Mr ₃):
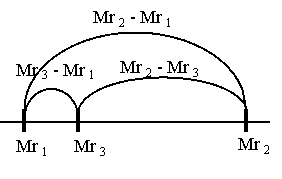3. Визначаємо довжини трьох відрізків:
4. Знаходимо обєми газів, що входять до суміші за формулами:

 

Спочатку знаходимо відносні молекулярні маси CH₄ та CO₂:

Mr(CH₄) = Ar(C) + 4Ar(H) = 12 + 4×1 = 16

Mr(CO₂) = Ar(C) + 2Ar(O) = 12 + 2×16 = 44

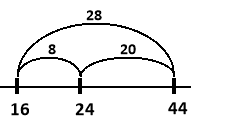Будуємо відрізки на яких вказуємо значення відносних молекулярних мас (по краям метану та вуглекислого газу, всередині – газової суміші) та знаходимо їх довжини:

Знаходимо об’єми газів:

 

Висновок

В заключній частині роботи хотілося б ще раз вказати на переваги використання правила  «коромисло Івашини» перед іншими способами:

• сфера застосування поширюється не тільки для розв’язування задач на суміші, компоненти яких перебувають в рідкому стані, а і на тверді та газоподібні суміші;
• для розв’язування задач введення змінних не потребується або їх використання зводиться до мінімуму;
• не треба проводити складних арифметичних розрахунків;
• графічна модель «коромисла Івашини» набагато простіша та зрозуміліша, ніж при використанні інших моделей.

P.S.

Колеги, якщо когось з вас зацікавив вказаний спосіб розв’язування задач, використовуючи правило «коромисло Івашини» та виникли запитання звертайтесь за електронною адресою igor19701970@ukr.net

Людина, що розуміє сутність задачі і використовує найбільш раціональний спосіб її розв’язку проявляє свою майстерність.

Бажаю успіху та стати справжніми майстрами!

З повагою Івашина Ігор Іванович.