Газета "Математична мозаїка" №№ 1 - 4

Рене Декарт

Рене́ Дека́рт (31 березня 1596 -11 лютого 1650) — французький філософ, фізик, фізіолог, математик, основоположник аналітичної геометрії. У математиці Декарт запровадив Декартову систему координат, дав поняття змінної величини і функції, ввів багато алгебраїчних позначень. У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили. Декарт — автор методу радикального сумніву в філософії, механіцизму у фізиці, передтеча рефлексології.

Цитати Рене Декарта

Прагни перемагати швидше самого себе, ніж долю, і змінювати своє бажання, ніж порядок у світі.

Я мислю — отже існую.

Правильно визначайте слова, і ви позбавите світ від половини непорозумінь.

Всі науки настільки пов’язані між собою, що легше вивчати їх всі відразу, ніж якусь одну із них окремо від інших.

Для того, щоб вдосконалити розум потрібно більше розмірковувати, ніж заучувати.

Мало мати хороший розум, головне — правильно його використовувати.

Це цікаво знати

     Щоб позначити дію множення  використовують знак "х". Його вперше використав у своїх роботах як знак, що означає множення, Оутред, а символ  з'явився в 1698 р. Його ввів німецький математик Готфрід Вільгельм Лейбніц.

     Знак ділення вперше ввів у 1202 р. в своїх роботах Леонардо Пізанський.

     Знаки додавання "+" і віднімання "-" застосовував лейпцизький професор Й. Відман (1489 р.). З початку XVII століття ці знаки набувають повсюдного визнання. За одним з вірогідних припущень знак "+" утворився з останньої літери латинського сполучника et("і")... За іншою версією, знаки "+" і "-"виникли з торговельної практики. Зокрема, виноторговці простими рисочками відзначали кількість мірок проданого з бочки вина. Коли ж якусь кількість мірок доливали, то відповідну кількість рисок перекреслювали.

     Найбільш уживаною і повсюдно поширеною в сучасному світі є, так звана, арабська (а точніше індійська) десяткова позиційна система. Відкриття десяткової позиційної системи відбулося в Індії, приблизно у VI ст. н.е. У VІІІ ст. це відкриття перейняли араби, які в той час володіли "усім світом" (це були часи Арабського Халіфату). Тільки з ХІІ ст. завдяки тим самим арабам десяткова система стала відомою в Європі.

     Цікаво, що нуль - єдине число, якому споруджено пам'ятник. У центрі Будапешта, поблизу одного із мостів, стоїть кам'яна статуя нуля. Напис "о км" на п'єдесталі символізує початок усіх доріг у країні. Зрештою, нуль розкрили як складне поняття, без якого неможливо уявити не тільки сучасну математику, а й популярні метафори: "нуль-ціна", "нуль без палички", "звести до нуля".

Магія чисел

1 x 8 + 1 = 9

12 x 8 + 2 = 98

123 x 8 + 3 = 987

1234 x 8 + 4 = 9876

12345 x 8 + 5 = 98765

123456 x 8 + 6 = 987654

1234567 x 8 + 7 = 9876543

12345678 x 8 + 8 = 98765432

123456789 x 8 + 9 = 987654321

Є таке дивне число: 142 857. Дивіться, при множенні в

ньому тільки міняються місцями цифри:

142 857 х 1 = 142 857

142 857 х 2 = 285 714

142 857 х 3 = 428 571

142 857 х 4 = 571 428

142 857 х 5 = 714 285

142 857 х 6 = 857 142

І тільки при множенні на 7 виходить 999 999.

До речі, 142 + 857 = 999, а 14 + 28 + 57 = 99.

І ще: 142 857 у квадраті буде 20408122449.

20408+122449 = 142 857

Це цікаво:

 111111111 Х 111111111 = 12345678987654321

           Число з давніх часів...

      Мало якому числу з усіх чисел приділяється стільки уваги, скільки приділяється числу π. Деякі навіть вважають його одним з п'яти найважливіших чисел в математиці.

      Число π – це відношення довжини кола до його діаметру. Грецькою літерою π це відношення вперше позначив в 1706 році англійський математик Вільям Джонс, а після того, як в 1737 році це позначення запозичив швейцарський математик Леонард Ейлер, воно стало загальноприйнятим. Для багатьох практичних цілей цілком достатньо використовувати шість знаків числа π (π = 3,14 159). Точне ж значення числа π обчислити неможливо – це ірраціональне число і його не можна написати у вигляді простого дробу. Якщо записувати його у вигляді десяткового дробу, то вона буде нескінченною. Число π можна обчислювати нескінченно, і в нього буде нескінченно багато десяткових знаків. Це не утримує математиків від утомливих спроб обчислити як можна більше десяткових знаків числа π. Більшості людей для роботи достатньо знати наближене значення - 3,14159. У XVIII столітті було точно підраховано 100 десяткових знаків, а в 1973 році два французьких математика вирахували мільйон десяткових знаків.

       Сьогодні Ясумаса Канада з Токійського університету отримав за допомогою комп'ютера більше шести мільярдів десяткових знаків. Важко навіть уявити, навіщо потрібно таке точне значення цього числа, оскількивсього 39 десяткових знаків достатньо для обчислення кола, що оперізує видимий Всесвіт, з похибкою, що не перевищує радіус атома водню. Якщо вимовляти без зупинки його підрахунки, то при швидкості одна цифра в секунду, знадобиться приблизно 200 років.

      Число π з'являється у багатьох формулах фізики, електротехніки, електроніки, теорії ймовірностей тощо. І здається, що подібно до того як немає кінця знаків числа π, так немає кінця і можливостям практичного застосування цього корисного, невловимого числа π.

Це цікаво знати

     Чи знаєте ви, що Шарль Перро, автор «Червоної Шапочки», написав казку «Любов циркуля і лінійки»?

     Чи знаєте ви, що Наполеон Бонапарт писав математичні роботи і один геометричний факт називається «Задача Наполеона»?

     Чи знаєте ви, що одна з кривих ліній називається «Локон Аньєзі» на честь першої у світі жінки-професора математики Марії Гаетани Аньєзі?

     Чи знаєте ви, що квітку гортензію назвали на честь Гортензії Лепот, відомої обчислювальниці, що складала математичні таблиці? Вона привезла цю квітку з Індії.

     Чи знаєте ви, що англійський математик Дж. Сильвестр написав сонет «Небесна муза», який він присвятив першій російській жінці-математику Софії Василівні Ковалевській?

     Чи знаєте ви, що Піфагор був переможцем з кулачного бою на 58-х Олімпійських іграх, які проходили в 548 році до н. е., а потім перемагав ще на декількох Олімпіадах?

     Чи знаєте ви, що знаменитий Фалес був спортивним уболівальником і помер на трибуні олімпійського стадіону під час бою Піфагора?

     Чи знаєте ви, що в 1940 році було надруковано книгу, в якій є 370 різних способів доведення теореми Піфагора, а серед них є доведення, яке запропонував президент США Гарфілд?

     Чи знаєте ви, що Франсуа Вієта майже було відправлено на вогнище за те, що йому пощастило розшифрувати таємне листування іспанського уряду з командуванням своїх військ? Іспанці вважали, що розкриття їхнього шифру людському розуму не під силу і Вієтові допомагав сам Сатана.

     Чи знаєте ви, що аристократи просили французького короля нагородити Рене Декарта, який першим запропонував метод нумерації крісел по рядах і місцях? Але король відповів: «Так, те, що винайшов Декарт, — чудово і гідно нагороди, але дати її філософу?! Ні, це вже занадто!».

Задачі для допитливих.

1. Розділити 10 апельсинів порівну між 12-ма особами, при умові, що різати кожний апельсин можна не більш як на 3 рівні частини.

2.  Собака женеться за кроликом, який знаходиться в 150 футах від неї. Вона робить стрибок на 9 футів щоразу, коли кролик стрибає на 7 футів. Скільки стрибків має зробити собака, щоб наздогнати кролика?

3. Скільки буде десятків, якщо два десятки помножити на два десятки?

4. Ви знаєте, скільки днів в січні? А ось уявіть собі, що місяць січень не закінчився, а триває і сьогодні - 35 січня. На який день лютого припаде це число?

5. Маленька стрілка на циферблаті годинника пересунулася на 45°. Скільки пройшло часу?

6. Електропотяг їде зі сходу на захід зі швидкістю 60 км за годину. У тому самому напрямі — зі сходу на захід — дме вітер, але зі швидкістю 50 км за годину. У якому напрямі відхиляється дим від потяга?

7. Два в квадраті - 4, три в квадраті - 9, чому дорівнює кут в квадраті?

8. Якою цифрою закінчується сума 16•17•18+31•32•33 ?

9. Двоє друзів зібралися поїхати на електричці за місто. Вони домовилися зустрітися в п'ятому вагоні. Проте вони не погодили, в п'ятому вагоні від початку чи від кінця потягу. І один сів в п'ятий вагон від початку, а другий - в п'ятий вагон від кінця. Але вони все-таки зустрілися. Скільки вагонів було в потягу?

Математична мозаїка №3

( Друковане видання математичного гуртка Машинобудівного коледжу СумДУ)

З історії тригонометрії.

Як і багато розділів математики, тригонометрія виникла в древні часи з потреб людей при веденні розрахунків, пов'язаних із земельними роботами (для визначення відстані до недоступних предметів, складання географічних карт і ін.). Ще старогрецькі  учені створили «тригонометрію хорд». Цією тригонометрією користувався в II ст до н.е. в своїх розрахунках старогрецький астроном Гиппарх.

      Довгі роки тригонометрія служила астрономії і розвивалася завдяки ній. У VIII ст. зусиллями математиків Близького і Середнього сходу тригонометрія виділилася з астрономії і стала самостійною математичною дисципліною. До цього часу хорди в тригонометрії були замінені синусами, були введені поняття косинуса і тангенса, а також складені таблиці значень тригонометричних функцій.

Слово «синус» сталося від латинського sinus («перегин»), яке, у свою чергу, походить від арабського слова «брехлива» («тятива лука»). Слово «косинус» – скорочення словосполуки complementi sinus («синус доповнення»), що пояснює той факт, що cos дорівнює синусу кута, доповнюючого кут до /2. Латинське слово  tangens переводиться як «дотична» («дотична до кола»).

Ідея введення тригонометричних понять за допомогою круга одиничного радіусу набула поширення в X-XI вв.

Перша наукова праця, в якій тригонометрія  утвердилась як самостійна гілка математики, була створена в 1462-1464 рр. німецьким астрономом і математиком І. Мюллером, відомим в історії під псевдонімом Региомонтан. Після Региомонтана значний вклад в тригонометрію вніс польський астроном і математик Н.Коперник (1473-1543), що присвятив цій науці два розділи своєї знаменитої праці «О зверненні небесних тіл» (1543).

Пізніше в творах І.Кеплера (1571-1630), Й.Бюрги (1552-1632),  Ф.Вієта (1540-1603) і  інших відомих матема-

тиків зустрічаються складні перетворення тригономет-ричних виразів і виводяться багато формул.

Тригонометрична символіка з роками удоско-налювалася і лише в праці Л.Ейлера в XVIII ст придбала сучасний вигляд, зручний для вирішення обчислювальних завдань.

         Дослідженням тригонометричних функцій практично займалися ще старогрецькі математики, вивчаючи взаємну зміну величин в геометрії і астрономії. Співвідношення між сторонами в прямокутних трикутниках, що за своєю суттю є тригонометричними функціями, розглядувалися вже в III ст до н.е. в роботах Евкліда, Архимеда, Аполонія і інших учених.Вчення про тригонометричні величини отримав розвиток в VIII-XV вв. у країнах Середнього і Ближнього Сходу. Так, в IX ст в Багдаді аль-Хорезми склав перші таблиці синусів. Аль-бузджані в X ст сформулював теорему синусів і з її допомогою побудував таблицю синусів з інтервалом 15’, в якій значення синусів приведені з точністю до 8-го десяткового знаку. Ахмад-аль-беруні в XI ст замість ділення радіусу на частини при визначенні значень синуса і косинуса, зробленого до нього Птоломєєм, зачав використовувати коло одиничного радіусу. У першій половині XV ст Аль-каши створив тригонометричні таблиці з кроком 1’, які подальші 250 років були неперевершеними по точності. За найкрупнішого європейського представника тієї епохи, що вніс вклад до розвитку дослідження тригонометричних функцій, вважається  Региомонтан.

Про властивості періодичності тригонометричних функцій знав ще Ф. Вієт. Швейцарський математик І. Бернуллі (1642-1727) в своїх роботах зачав застосовувати символіку тригонометричних функцій. Проте близьку до прийнятої тепер ввів Л. Ейлер в 1748 р. в своїй роботі «Введення в аналіз нескінченних». У ній він розгледів питання про знаки всіх тригонометричних функцій будь-якого аргументу.

В XVII-XIX вв. тригонометрія поступово увійшла до складу математичного аналізу і почала широко використовуватися в механіці і техніці.

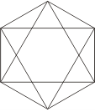
РОЗВ’ЯЖІТЬ:

    1. Полічіть, скільки трикутників у фігурі, яка зображена на малюнку:

2. 2. У пастуха,  який  вів 70  биків,  запитали: "Яку частину биків своєї численної череди ти ведеш?" Він відповів: "Я веду дві третини від третини худоби". Скільки биків було у всій череді?
   3.                                3. Малюк і Карлсон розділили круглий торт двома пер-пендикулярними прямолінійними розрізами на 4 частини. Карлсон узяв собі одну найменшу частину і одну найбільшу, а інші дві віддав Малюкові. Кому з них дісталося не менше половини торта?
   4.         4. У  кодовому замку  є чотири кнопки  з цифрами 1, 2, 3,
   5.   4. Код, який відкриває замок, є чотирицифровим. Яку найменшу кількість разів слід натиснути на кнопки, щоб напевно визначити правильний код? Замок відкривається тільки в тому випадку, коли у правильному порядку натиснуто всі цифри коду. Після неправильного набору коду натиснення  кнопок анулюється.
   6. Яке з наведених тверджень є хибним?

Математична мозаїка №4

( Друковане видання математичного гуртка Машинобудівного коледжу СумДУ)

Джон Непер

(1550—1617)

Закінчив Сент-Ендрюський  університет, куди він вступив в 1563 році. З 1571 року живе в своєму рідному замку в Шотландії. Весь його час було присвячено заняттям богословськими предметами і математикою. За його власними словами, тлумачення пророцтв завжди складало головний предмет його занять, математика ж служила для нього тільки відпочинком.

Тим не менш Непер увійшов в історію як винахідник чудового обчислювального інструмента – таблиці логарифмів. Це відкриття викликало гігантське полегшення праці обчислювача. Крім того, воно призвело до появи нової трансцендентної функції і показало приклад рішення диференціального рівняння.

Лаплас говорив, що Непер своїм винаходом «продовжив життя астрономів», спростивши їх обчислення. Інші захоплення вченого:

• чималу популярність отримав придуманий Непер оригінальний прилад для швидкого множення (палички Непера);
• Непер займався також астрономією, астрологією і богослов'ям. Його тлумачення Апокаліпсиса: «A plaine discovery of the whole revelation of S. John etc.»вийшло в Едінбургу, в 1593 р. Воно написано в математичній формі. Зокрема, 26-а теорема стверджувала, що Папа є Антихрист, 36-а - що згадувана в Апокаліпсисі сарана означає турок і арабів. Кінець світу, як довів автор, повинен мати місце між 1688 і 1700 роками. Книга мала незрівнянно більший успіх, ніж усі наукові твори автора. З'явилося декілька її перекладів за межами Щотландії.

На честь Джона Непера названі логарифмічна безрозмірна одиниця, кратер на Місяці, університет в Единбурзі (Edinburgh Napier University), астероїд 7096 Непер (1992 рік).

Винахід логаріфмічної лінійки

Не варто забувати, що саме за допомогою логарифмічної лінійки людина вперше ступила на Місяць.

Вільям Отред, випускник Ітонської школи й Кембриджського королівського коледжу, пастор церкви в Олсбері в графстві Суррей, був жагучим математиком і із задоволенням викладав улюблений предмет численним учням, з яких не брав ніякої плати.

       Один раз, обговорюючи «механічні обчислення» за допомогою лінійки Гюнтера зі своїм учнем Вільямом Форстером, Отред відзначив недосконалість цього методу. І вчитель продемонстрував свій винахід – кілька концентричних кілець із нанесеними на них логарифмічними шкалами й двома стрілками. Отред говорив, що він «просто зігнув і згорнув шкалу Гюнтера в кільце», і до того ж був упевнений, що «сьогодення мистецтво математики не має потреби в інструментах...», їхнє використання він уважав припустимим тільки після оволодіння цим мистецтвом. Учень настояв на публікації, і в 1632 році Отред написав (на латині), а Форстер перевів на англійський брошуру «Кола пропорцій і горизонтальний інструмент», де була описана логарифмічна лінійка.

Ще один претендент на авторство – лондонський математик Едмунд Уінгейт, що запропонував в 1626 році використовувати дві лінійки Гюнтера, що сковзають відносно один одної. До сучасного стану інструмент довели Роберт Біссакер, що зробив лінійку прямою (1654), Джон Робертсон, що забезпечив її бігунком (1775), і Амеде Маннгейм, який оптимізував розташування шкали і бігунка.

Логарифмічна лінійка значно полегшила складні обчислення для інженерів і вчених. В XX столітті до появи калькуляторів і комп'ютерів логарифмічна лінійка було таким самим символом інженерних спеціальностей, яким для лікарів є фонендоскоп.

Знайдіть помилку

  Нехай a = b.

 Перемножимо обидві частини на a:

a² = ab

Віднімемо від обох частин b²:

a² - b² = ab - b²

Тоді можна розкласти ліву частину і винести за дужки b в правій частині:

(a + b)(a - b) = b(a - b)

Скорочуємо:

a + b = b

Оскільки a = b, то замінюємо a на b:

2b = b

Скорочуємо на b:

Отже:  2 = 1

ВИКЛАДАЧІ ЖАРТУЮТЬ...

     У навчальному закладі викладача  математики заміняє викладач  фізкультури і запитує:

- Діти, скільки буде 5х5?

- 30.

- Ні діти, 5х5 - буде 25, ну 26, ну в крайньому випадку 27, але ніяк не 30.

*****

Викладач:

- Тема сьогоднішнього уроку - "Розв’язок логаричмічних  рівнянь".

Весь клас:

- У-у-у...

Викладач:

- Hу добре, добре, наприкінці трохи потанцюємо і послу-хаємо музику.

*****