Матеріал до уроків "Повторення теми «Рівняння з параметрами» при підготовці до зовнішнього незалежного тестування"
Повторення теми «Рівняння з параметрами» при підготовці до зовнішнього незалежного тестування.
Будь-яке рівняння або нерівність з параметрами можна вирішувати як звичайне рівняння або нерівність доти, поки всі міркування або перетворення, необхідні для вирішення, можна виконувати однозначно. Якщо якесь перетворення не можна виконати однозначно, то рішення необхідно розбити на кілька випадків, щоб в кожному з них відповідь через параметри записувалася однозначно.
Особливості рішень рівнянь з параметрами в порівнянні з рівняннями що не містять параметрів, в основному сходяться до двох:
1. Крім відшукання області D визначення рівняння вказуються також області зміни D1, D2 ... для кожного з параметром а1, а2 відповідно
2. Для будь-якого знайденого кореня вказуються області зміни параметрів а1, а2 при яких даний корінь входить в рішення рівняння.
Зверніть увагу, що для відшукання безлічі значень параметра, при якому існують корені рівняння, необхідно, крім розгляду умов, при яких існує рівняння в залежності від параметрів і умов, що входять в область визначення D рівняння, розглядати також і умови існування коренів.
У деяких випадках умови, яким повинні задовольняти параметри, щоб рівняння існувало, важко вказати при розгляді початкового рівняння і вони визначаються або уточнюються в процесі рішення рівняння.
Повторювати матеріал варто почати з найпростіших і більш зрозумілих квадратних рівнянь.
1. При якому значенні параметра а корені рівняння 3х2 + 2ах − а2 = 0
знаходяться в інтервалі [0; 1]
Стандартно вирішуємо рівняння:
D = 4𝑎2 + 12𝑎2 = 16𝑎2 = (4𝑎)2
Ми бачимо, що х1 и х2 мають різні знаки і не можуть одночасно потрапити в додатний інтервал.
Відповідь: рішення немає.
2. При якому значенні параметра 𝑎 корені рівняння 𝑎х2 + 2х − 𝑎 = 0 знаходяться в інтервалі [1; 2]
Стандартно вирішуємо рівняння: D = 4 + 4𝑎2
Досліджуємо знайдені корені - знаходимо значення параметру, при якому корені рівняння потрапляють в заданий інтервал
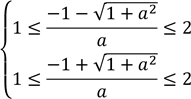
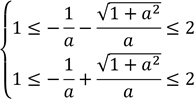
додаємо до першої другу нерівність, отримуємо 
далі 
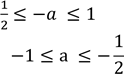
Відповідь: якщо 
то
[1; 2]
3. При якому значенні параметра 
корені рівняння 
будуть рівні?
Якщо дискримінант дорівнює 0, тоді корені будуть рівні
Бачимо, що 
, якщо 
Відповідь: якщо 
, то корені рівняння будуть рівні
4. При якому значенні параметра 
корені рівняння 
будуть дійсними числами?
Поперше відзначимо, так як параметр 
стоїть під знаком логарифму, визначаємо область зміни параметру: 
Якщо дискримінант 
, рівняння матиме дійсні корені. Знаходимо D
4 − 4 log2 𝑎 ≥ 0 ⇔ 4(1 − log2 𝑎) ≥ 0 ⇔ log2 𝑎 ≤ 1 ⇔ 𝑎 ≤ 2 та враховуючи умову 𝑎 > 0 маємо
Відповідь: якщо 𝑎 є (0; 2) то рівняння буде мати два дійсних корені, якщо 𝑎 = 2 то рівняння буде мати один дійсний корінь.
5.При якому значенні параметра 𝑎 корені рівняння х2 − 2𝑎х − 𝑎 + 2 = 0 буде мати два від’ємних кореня?
Щоби знайти відповідь потрібно перерахувати умови, за яким ми будемо шукати корені. Це – додатний дискримінант, щоб було два кореня, та згідно теоремі Вієта доданок (коефіцієнт с наведеного квадратного рівняння) двох від’ємних чисел є додатне число та сума (коефіцієнт b наведеного квадратного рівняння) двох від’ємних чисел є від’ємне число. У нашому рівнянні : 𝑏 = −2𝑎, 𝑐 = −𝑎 + 2
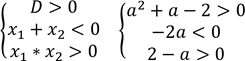𝑥 < −2 або 𝑥 > 1
{ 𝑎 > 0
𝑎 < 2
У відповідь об’єднуємо проміжки та визначаємося
Відповідь: рівняння має два від’ємних кореня, якщо 1 < 𝑎 < 2
Рівняння з модулями
1. Розв’язати рівняння |x+a|=2
По параметру а немає ніяких обмежень, розв’язуємо звичайно:
х+а=2 або х+а=-2 та далі х1=2-а або х2= -2-а
Відповідь: для будь-якого значення а рівняння має два корені х1=2-а або х2= -2-а
2. Розв’язати рівняння |1-x|=а
Параметр а дорівнює модулю, отже 𝑎 ≥ 0 і далі
Згідно означенню модуля: 1-х=а або 1-х=-а , звідки х1=1-а або х2=1+а Відповідь: за умови 𝑎 > 0 рівняння має два розв’язки х1=1-а або х2=1+а, за умовою а=0 рівняння має один розв’язок х1=1
3. Яку кількість розв’язків може мати рівняння |𝑥2 − 8|𝑥| + 12| = 𝑎 в залежності від значення параметру 𝑎.
Будемо шукати рішення графічно.
Побудуємо графіки функцій 𝑦 = |𝑥2 − 8|𝑥|+12| та 𝑦 = 𝑎
Починаємо з побудови графіку 𝑦 = 𝑥2 − 8𝑥 + 12 – вершина параболи має координати (4;-4), корені x1 =2 x2 =6 та перетинає ось у точці y=12
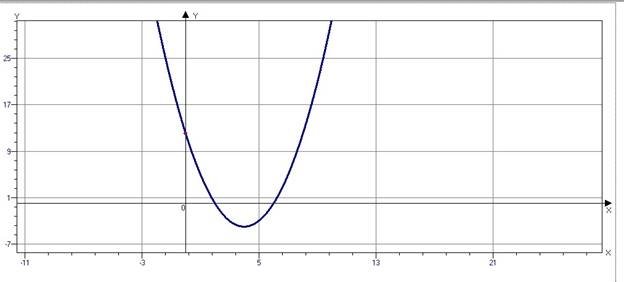
Послідовно перетворюємо графік функції 𝑦 = 𝑥2 − 8|𝑥| + 12 відображаємо симетрично частину графіка для х > 0 відносно осі y
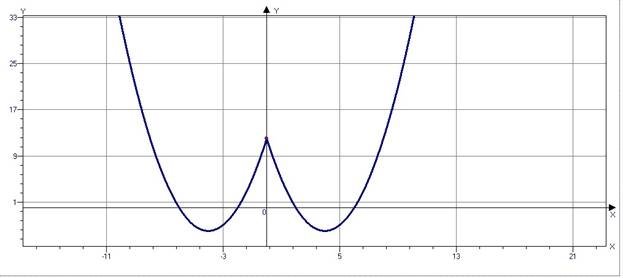
𝑦 = |𝑥2 − 8|𝑥| + 12| відображаємо симетрично частину графіка для y < 0 відносно осі х
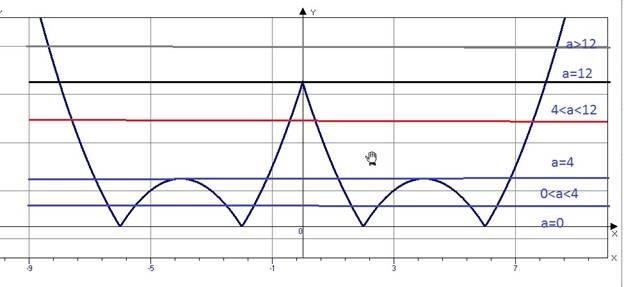
Додаємо різні варіанти розташування прямої та визначаємося з відповіддю
Якщо 𝑎 = 0 та 4 < 𝑎 < 12 то рівняння має 4 рішення;
Якщо 0< 𝑎 < 4 то рівняння має 8 рішень;
Якщо 𝑎 = 4 то рівняння має 6 рішень; Якщо 𝑎 = 12 то рівняння має 3 рішення; Якщо 𝑎 > 12 то рівняння має 2 рішення.
4. При якому значенні параметру 𝑎 рівняння має один розв’язок
𝑥|𝑥 − 2𝑎| − 3𝑎 + 2 = 0
Визначаємо область допустимих значень для параметру 𝑎, 𝑎 ∈ 𝑅
Якщо записати 𝑥|𝑥 − 2𝑎| = 3𝑎 − 2 , тоді будемо розв’язувати це рівняння за допомогою графіків 𝑦 = 𝑥|𝑥 − 2𝑎| та 𝑦 == 3𝑎 − 2
Розбиваємо рішення на дві частини: враховуючи означення модуля
𝑦 = 𝑥2 − 2𝑎х має вершину у точці 𝑥0 = 𝑎, 𝑦0 = −𝑎2, нуліx1 = 0 𝑥2 = 2𝑎
𝑦 = −𝑥2 + 2𝑎х має вершину у точці 𝑥0 = −𝑎, 𝑦0 = 𝑎2,нуліx1 = 0 𝑥2 = −2𝑎 та виконуємо побудову графіку
З урахуванням знаку 𝑎 маємо:
𝑎 ≥ 0
1) { 𝑥 ≥ 2𝑎 𝑦 = 𝑥2 − 2𝑎х
⌊𝑥 < 2𝑎 𝑦 = −𝑥2 + 2𝑎х
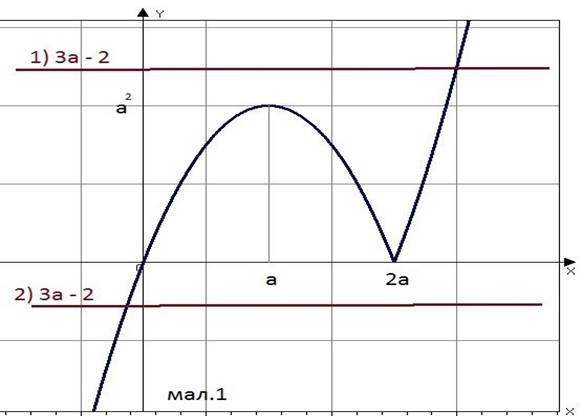
Бачимо на малюнку , що можемо мати єдиний корінь за умови
Нерівність 𝑎2 − 3𝑎 + 2 < 0 виконується, якщо 1 < a < 2 та маємо, що перша система має цей розв’язок.
Розв’язок другої системи 
2) Так само розглядаємо й умову a < 0
𝑎 < 0
{ 𝑥 ≥ 2𝑎 𝑦 = 𝑥2 − 2𝑎х
⌊𝑥 < 2𝑎 𝑦 = −𝑥2 + 2𝑎х
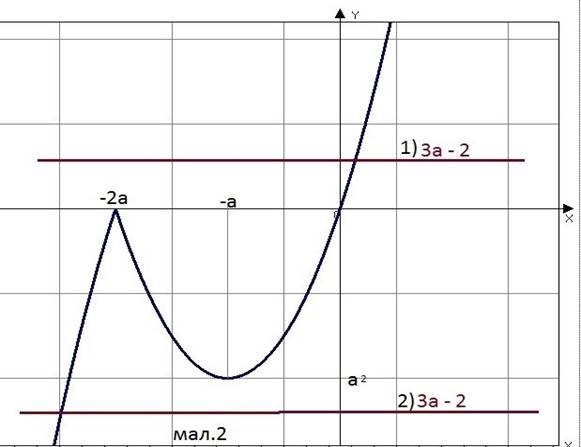
Маємо єдине рішення, якщо
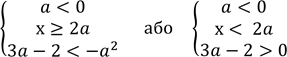
Перша система:
𝑎2 + 3𝑎 − 2 < 0
D = 0 якщо 
,
Рішення цієї нерівності 
та з урахуванням умови, що
𝑎 < 0 система має розв’язок 
Друга система має несумісні умови та розв’язку не має.
Отже, об’єднуємо проміжки та отримуємо остаточну відповідь:
Рівняння буде мати один корінь, якщо параметр 
Ірраціональні рівняння з параметрами.
1. При якому значенні параметра 𝑎 рівняння має дійсні корені
√𝑥2 − (5𝑎 − 4)𝑥 − 12 = 𝑥 + 2 ?
Визначаємо область допустимих значень для 𝑥 : 𝑥 ≥ −2
Визначаємо область допустимих значень для параметру 𝑎
𝑥2 − (5𝑎 − 4)𝑥 − 12 ≥ 0
𝐷 = (5𝑎 − 4)2 − 4 ∗ (−12) = 25𝑎2 − 40𝑎 + 48 + 16 = 25𝑎2 − 40𝑎 + 64 ≥ 0
Досліджуємо, 𝐷(𝑎) = 400 − 1600 < 0
Отже, квадратична нерівність 𝑥2 − (5𝑎 − 4)𝑥 − 12 ≥ 0 виконується для будь-якого 𝑎
Розв’язуємо наше рівняння, знаходимо корінь
√𝑥2 − (5𝑎 − 4)𝑥 − 12 = 𝑥 + 2
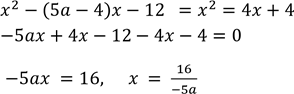
Визначаємося з 𝑎, за умови : 𝑥 ≥ −2
маємо: 𝑎 < 0 або 𝑎 ≥ 1,6
Відповідь: якщо 𝑎 < 0 або 𝑎 ≥ 1,6 рівняння має один корінь 
,
2. Розв’язати рівняння 
Умови існування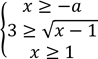 
або 
Знаходимо корінь 
У цьому місці маємо додаткове обмеження по 𝑎:
8 − 𝑎 ≥ 0 або 𝑎 ≤ 8
Далі 36(𝑥 − 1) = 64 − 16𝑎 + 𝑎2 та маємо 
Перевіряємо умови
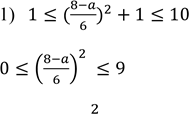
ця умова виконується завжди,
Умова 2) 
𝑎2 − 16𝑎 + 64 + 36 + 36𝑎 ≥ 0
𝑎2 + 20𝑎 + 100 ≥ 0
(𝑎 − 10)2 ≥ 0 виконується для будь-якого значення параметру 𝑎
Умова 3) 𝑎 ≤ 8
Об’єднуємо умови та записуємо відповідь:
Рівняння має один корінь 
, якщо −10 ≤ 𝑎 ≤ 8
Та немає коренів, якщо 𝑎 ≤ −10 або 𝑎 ≥ 8
Цікаві раціональні рівняння з параметрами:
1. Розв’язати рівняння з параметром
Умови 𝑎 ≠ 0 та 𝑥 ≠ 0
4 3 3 2 2 2 2
Перетворимо та далі
𝑥4 + 𝑏3𝑎3 − 𝑏𝑎2𝑥2 − 𝑏2𝑎𝑥2 = 0 – біквадратне рівняння
Нехай 
𝑡2 − (𝑏𝑎2 + 𝑏2𝑎)𝑡+𝑏3𝑎3 = 0
𝐷 = (𝑏𝑎2 + 𝑏2𝑎)2 − 4𝑏3𝑎3 = 𝑎2𝑏2(𝑏 + 𝑎)2 − 4𝑏3𝑎3
= 𝑎2𝑏2(𝑏2 + 2𝑎𝑏 + 𝑎2 − 4𝑎𝑏) = 𝑎2𝑏2(𝑏2 − 2𝑎𝑏 + 𝑎2)
= 𝑎2𝑏2(𝑏 − 𝑎)2 = (𝑎𝑏(𝑎 − 𝑏))2
Знаходимо 
𝑡1 = 𝑏2𝑎 звідки 
𝑡2 = 𝑎2𝑏 звідки 
Зараз повертаємося назад к області допустимих значень та перевіряємо виконання 𝑥 ≠ 0. Отже, відповідь
, якщо 𝑎 > 0 та 𝑏 ≠ 0 або 𝑥 = ±ab, якщо 𝑏 > 0 та 𝑎 ≠ 0
2. Розв’язати рівняння з параметром
Область допустимих значень x ≠ −3
Розглянемо варіанти
1) p = −1 немає коренів
2) Визначимося, при якому значенні параметру 
у правій частині можна призвести скорочення на займенник, це 
, виконуємо 
Та
отримуємо 
x=2p+5
Маємо один розв’язок при 
3) 
виконуємо стандартні дії для рішення раціонального рівняння
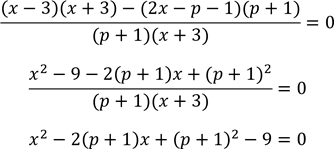
та 
Відповідь: якщо 
, то ріввняння немає коренів, при 
маємо
один розв’язок 
, при 
та
два корені 
та
Робота учителя математики приватної школи
«Привилегия» м.Маріуполь
ВАЛЕНТИНИ Вікторівни
Абрамової
про публікацію авторської розробки
Додати розробку