Презентація "Рівняння дотичної"

Тема уроку: Рівняння дотичної.

ху0y = f (x) х0f(x0)M0 Задача про дотичну до графіка функції.y = k x + b З курсу геометрії 9 класу відомо,що рівняння невертикальної прямої має вигляд: y = kx + b. Використовуючи геометричнийзміст похідної, маємо: k = fʹ(х0). Тоді рівняння дотичної можемозаписати в такому вигляді:y = fʹ(х0)x + b. Оскільки пряма проходить через точку M0 (х0; f(х0)), то їїкоординати задовольняють рівняння прямої. Отже, будемо мати: f(х0) = fʹ(х0)х0 + b.

Звідки виражаємо b: b = f(х0) - fʹ(х0) х0. Підставимо значення b в рівняння дотичної:у = fʹ(х0) x + f(х0) - fʹ(х0) х0,у = fʹ(х0)(x - х0) + f(х0) – рівняння дотичної, проведеної дографіка функції з абсцисою х0.

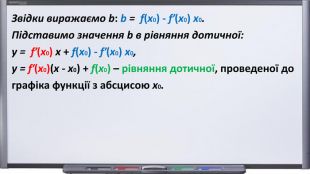
Приклад [ЗНО 2018]. Задано функцію f(х) = х2 – 3х – 4. Знайдіть значення х = х0, за якого похідна функції f дорівнює 1. Запишітьрівняння дотичної, проведеної до графіка функції f у точці з абсцисою х0. Розв’язування.у = fʹ(х0)(x - х0) + f(х0). fʹ(х0) = (х0 2 – 3х0 – 4 ) ʹ = 2х0 –3; 2х0 – 3 = 1, х0 = 2. f(х0) = х0 2 – 3х0 – 4 = 4 – 6 - 4 = - 6. Підставимо отримані значення в рівняння дотичної:у = fʹ(х0)(x - х0) + f(х0); у = 1(x - 2) + (- 6) = х – 8. Відповідь: у = х – 8.

Приклад. Складіть рівняння дотичної до графіка функції f(х) = х2 + 3х – 5, яка паралельна прямій у = 7х - 2. Розв’язування.у = fʹ(х0)(x - х0) + f(х0). Оскільки дотична паралельна прямій у = 7х - 2, то k = fʹ(х0) = 7. Знайдемо абсцису точки, в якій проведено дотичну, до графіка заданої функції. fʹ(х0) = (х0 2 + 3х0 – 5 ) ʹ = 2х0 + 3; 2х0 + 3 = 7, х0 = 2. f(х0) = х0 2 + 3х0 – 5 = 4 + 6 - 5 = 5. Підставимо отримані значення в рівняння дотичної:у = fʹ(х0)(x - х0) + f(х0); у = 7(x - 2) + 5 = 7х - 9. Відповідь: у = 7х – 9.

Приклад. Складіть рівняння дотичної до графіка функції f(х) = - х2 + 3, яка проходить через точку С(1; 3). Розв’язування.у = fʹ(х0)(x - х0) + f(х0).fʹ(х0) = (- х0 2 + 3) ʹ = - 2х0; f(х0) = - х0 2 + 3. Підставимо отримані вирази в рівняння дотичної:у = - 2х0(x - х0) + (- х0 2 + 3). Оскільки дотична проходитьчерез т. С(1; 3), то її координати задовольняють рівняннядотичної. Маємо: 3 = - 2х0(1 - х0) + (- х0 2 + 3). Звідки х0 = 0 або х0 = 2. Тоді у = 3 або у = - 4х + 7. Відповідь: у = 3 або у = - 4х + 7.

Розв’язуємо самостйно:§ 7, п.46 № 46.1(1), № 46.3(1), № 46.7, № 46.10(1), № 46.31.

Домашня робота:§ 7, п. 46 № 46.2(1), № 46.4(1), № 46.8, № 46.11(1), № 46.32.

4 Здобувайте знання дистанційно із задоволенням!Бережіть себе!Мийте руки!Слухайте маму!

4 Презентація створена вчителем математики. Житомирського міського ліцею №1 ЖМРПанським Володимиром Анатолійовичем2021