Матеріали для проведення факультативних занять з математики у 9 класі
В даній розробці зібрано і систематизовано як теоретичний матеріал так і приклади розв'язання задач з тем, які планується розглядати на факультативних заняттях з математики.
Матеріали
для проведення
факультативних занять
з математики
у 9 класі
Підготувала
вчитель математики
загальноосвітньої школи
І – ІІ ступеня смт Шацьк
Гуж Марія Михайлівна
ЗМІСТ
|
І. |
Історія математики |
1 |
|
|
|
1. |
Основні етапи розвитку математики. Історія розвитку поняття функції. Історія розвитку сучасних розділів математики: комбінаторики, теорії ймовірностей, математичної статистики, топології, фрактальної геометрії й фрактального аналізу. Розвиток математики в Україні. |
1 |
|
|
2. |
Розв’язування історичних задач |
37 |
|
II. |
Математична мозаїка |
40 |
|
|
|
1. |
Послідовність Фібоначчі. Сніжинка Коха. Килим Серпинського. Геометрія орнаментів і паркетів. Паркети і сітки з чотирикутників |
40 |
|
|
2. |
Три визначні задачі давнини. Розв'язування олімпіадних задач. |
53 |
|
IV. |
Нерівності |
63 |
|
|
|
1. |
Раціональні нерівності зі змінною. Метод інтервалів. |
63 |
|
|
2. |
Ірраціональні нерівності. |
73 |
|
|
3. |
Нерівності, що містять змінну під знаком модуля. |
81 |
|
|
4. |
Нерівності з параметрами. |
83 |
|
|
5. |
Доведення нерівностей. |
89 |
|
V. |
Системи рівнянь і нерівностей |
98 |
|
|
|
1. |
Детермінанти (визначники), їх обчислення. Системи лінійних рівнянь. Перші уявлення про лінійне програмування. |
98 |
|
|
2. |
Системи симетричних рівнянь. Системи діофантових рівнянь. |
104 |
|
|
3. |
Системи ірраціональних рівнянь і основні методи їх розв'язування. |
112 |
|
VI. |
Функції |
117 |
|
|
|
1. |
Поняття функції. Побудова графіків функцій. Лінійні перетворення функцій та їх графіків. |
117 |
|
|
2. |
Побудова графіків функцій, що містять знак модуля. |
127 |
|
|
3. |
Графічне розв'язування рівнянь, нерівностей та їх систем. |
128 |
|
|
4. |
Побудова графіків рівнянь з модулями. |
132 |
|
|
5. |
Графічне розв'язування рівнянь та систем рівнянь, що містять параметри |
135 |
|
VII. |
Метод математичної індукції |
139 |
|
|
|
1. |
Індукція і дедукція. Повна і неповна індукція. Недостатність неповної індукції. Принцип математичної індукції. Метод математичної індукції |
139 |
|
|
2. |
Принцип математичної індукції. Приклади доведень методом математичної індукції. |
141 |
|
VII. |
Комбінаторика |
154 |
|
|
|
1. |
Предмет комбінаторики. Комбінаторні правила множення, додавання і доповнення. Перестановки, розміщення, комбінації. Трикутник Паскаля. Біном Ньютона. |
154 |
|
|
2. |
Комбінаторні вирази та їх перетворення. Доведення комбінаторних тотожностей. Розв'язування комбінаторних рівнянь. Розв'язування комбінаторних задач. |
162 |
|
VIII. |
Подібність та інверсія |
167 |
|
|
|
1. |
Симетрія подібності навколо нас. Перетворення подібності, його властивості. Означення і властивості перетворення подібності. Подібність фігур |
167 |
|
|
2. |
Гомотетія, її властивості. Ознаки гомотетії. Означення і задання гомотетії. Властивості гомотетії. Три попарно гомотетичні фігури. |
171 |
|
|
3. |
Застосування подібності у процесі розв'язування задач. |
176 |
|
|
4. |
Інверсія, її властивості. Побудова образів фігур при інверсії |
184 |
|
|
5. |
Поняття інверсії. Властивості інверсії. Інверсія точки. Інверсія прямої і кола. Основна властивість інверсії. Координатні формули інверсії. |
184 |
|
|
6. |
Застосування інверсії у процесі розв'язування задач. |
193 |
|
IX. |
Цікаві теореми геометрії |
197 |
|
|
|
1. |
Різні доведення теореми Піфагора. Узагальнення теореми Піфагора. |
197 |
|
|
2. |
Теорема Чеви, Менелая та Птолемея. Застосування теорем у розв’язанні задач. |
202 |
|
|
3. |
Теорема Дезарга. Теореми Паскаля і Бріаншона. |
222 |
|
X. |
Розв’язування задач підвищеної складності |
228 |
|
І.І. Історія математики
1. Основні етапи розвитку математики.
В історії математики традиційно виділяються декілька етапів розвитку математичних знань:
1. Формування поняття геометричної фігури і числа як ідеалізації реальних об'єктів і безлічі однорідних об'єктів. Виникнення лічби і вимірювання, які дозволили порівнювати різні числа, довжини, площі і об'єми.
2. Винайдення арифметичних операцій. Накопичення емпіричним шляхом (методом проб і помилок) знань про властивості арифметичних дій, про способи вимірювання площ і об’ємів простих фігур і тіл. В цьому напрямі далеко просунулися вавілонські, китайські і індійські математики давнини.
3. Поява в стародавній Греції дедуктивної математичної системи, що показала, як отримувати нові математичні істини на основі вже існуючих. Вінцем досягнень старогрецької математики стали «Начала» Евкліда, що відігравали роль стандарту математичної освіти протягом двох тисячоліть.
4. Математики країн Ісламу не тільки зберегли античні досягнення, але і змогли здійснити їх синтез з відкриттями індійських математиків, які в теорії чисел просунулися далі за греків.
5. В XVI—XVIII століттях відроджується і йде далеко уперед європейська математика. Її концептуальною основою в цей період була упевненість в тому, що математичні моделі є свого роду ідеальним скелетом Всесвіту, і тому відкриття математичних істин є одночасно відкриттям нових властивостей реального світу. Головним успіхом на цьому шляху стала розробка математичних моделей залежності (функція) і прискореного руху (аналіз нескінченно малих). Всі природні науки були перебудовані на базі нововідкритих математичних моделей, і це привело до колосального їх прогресу.
6. В XIX—XX століттях стає зрозуміло, що взаємовідношення математики і реальності далеко не таке просте, як раніше здавалося. Не існує загальновизнаної відповіді на свого роду «основне питання філософії математики»: знайти причину «незбагненної ефективності математики в природничих науках». В цьому, і не тільки в цьому, відношенні математики розділилися на безліч дискутуючих шкіл. Виділилося декілька небезпечних тенденцій: надмірно вузька спеціалізація, ізоляція від практичних задач і ін. В той же час потужність математики і її престиж, підтриманий ефективністю застосування, високі як ніколи раніше.
Крім великого історичного інтересу аналіз еволюції математики представляє величезну важливість для розвитку філософії і методології математики. Нерідко знання історії сприяє і прогресу конкретних математичних дисциплін; наприклад, стародавня китайська задача (теорема) про остачі сформувала цілий розділ теорії чисел.
Виникнення арифметики і геометрії
Математика в системі людських знань є розділом, що займається такими поняттями, як кількість, структура, співвідношення і т. п. Розвиток математики почався із створення практичного мистецтва рахунку і вимірювання ліній, площ і об’ємів.
Поняття про натуральні числа формувалося поступово і ускладнювалося невмінням первісної людини відділяти числову абстракцію від її конкретного уявлення. Внаслідок цього рахунок довгий час залишався тільки речовинним — використовувалися пальці, камінчики, помітки і т. п. Археолог Б. А. Фролов обгрунтовує існування рахунку вже в ранньому палеоліті.
З розповсюдженням рахунку на більші кількості з'явилася ідея користуватися не тільки одиницями, але і, так би мовити, пакетами одиниць, що містять, наприклад, 10 об'єктів. Ця ідея негайно відобразилася в мові, а потім і в писемності.
Для запам'ятовування результатів в рахунку використовували карби, вузлики і т. п. З винаходом писемності стали використовувати букви або особливі значки для скороченого зображення великих чисел. При такому кодуванні звичайно відтворювався той же принцип нумерації, що і в мові.
Назви чисел від двох (zwei, two, duo, deux, dvi, два.) до десяти, а також десятків і числа 100 в індоевропейських мовах схожі. Це говорить про те, що поняття абстрактного числа з'явилося дуже давно, ще до розділення цих мов. При утворенні чисел у більшості народів число 10 займає особливе положення, так що зрозуміло, що рахунок по пальцях був широко поширений. Звідси походить поширена десяткова система числення. Хоча є і виключення: 80 по-французьки quatre-vingt (тобто 4 двадцятки), а 90 — quatre-vingt-dix (4*20+10); це вживання сходить до рахунку по пальцях рук і ніг. Аналогічно утворюються числа датської, осетинської, абхазької мов. Ще зрозуміліше з лічбою двадцятками в грузинській мові. Шумери і ацтеки, судячи з мови, спочатку рахували п'ятірками.
Є і більш екзотичні варіанти. Вавілоняни в рахунках використовували шестидесяткову систему. А тубільці островів Торресова протоки — двійкову:
Урапун (1); Окоза (2); Окоза-Урапун (3); Окоза-Окоза (4) Окоза-Окоза-Урапун (5); Окоза-Окоза-Окоза(6)
Коли поняття абстрактного числа остаточно затвердилося, наступним кроком стали операції з числами. Натуральне число — це ідеалізація кінцевої множини однорідних, стійких і неподільних предметів (людей, овець, днів і т. п.). Для лічби важливо мати математичні моделі таких найважливіших подій, як об'єднання таких множин в одне або, навпаки, відділення частини множини. Так з'явилися операції додавання і віднімання. Множення для натуральних чисел з'явилося в якості, так би мовити, пакетного додавання. Властивості і взаємозв'язок операцій відкривалися поступово.
Інша важлива практична дія — розділення на частини — з часом абстрагувалося в четверту арифметичну операцію — ділення. Ділити на 10 частин складно, тому десяткові дроби, зручні в складних обчисленнях, з'явилися порівняно пізно. Перші дроби звичайно мали знаменником 2, 3, 4, 8 або 12. Наприклад, у римлян стандартним дробом була унція (1/12). Середньовічні грошові і мірні системи несуть на собі явний відбиток стародавніх недесяткових систем: 1 англійський пенс = 1/12 шилінга, 1 дюйм = 1/12 фута, 1 фут = 1/3 і т. д.
Майже в той же час, що і числа, людина абстрагувала плоскі і просторові форми. Вони звичайно одержували назви схожих з ними реальних предметів: наприклад, у греків «ромбос» означає дзига, «трапедсіон» — столик (трапеція) «сфера» — м'яч.
Теорія вимірювань з'явилася значно пізніше, і нерідко містила помилки: характерним прикладом є помилкове вчення про рівність площ фігур при рівності їх периметрів, і навпаки. Це недивно: вимірювальним інструментом була мірна мотузка з вузлами або помітками, так що виміряти периметр можна було без праці, а для визначення площі в загальному випадку ні інструментів, ні математичних методів не було. Вимірювання служили найважливішим застосуванням дробових чисел і джерелом розвитку їх теорії.
Єгипет
Найдавніші давньоєгипетські математичні тексти відносяться до початку II тисячоліття до н. е. Математика тоді використовувалася в астрономії, мореплавстві, землемірстві, при будівництві будинків, дамб, каналів і військових укріплень. Грошових розрахунків, як і самих грошей, в Єгипті не було. Єгиптяни писали на папірусі, який зберігається погано, і тому в даний час знань про математику Єгипту істотно менше ніж про математику Вавілону або Греції. Ймовірно, вона була розвинута краще, ніж можна уявити, виходячи з документів що дійшли до нас, підтверджується, що грецькі математики вчилися у єгиптян.
Основні джерела, що збереглися: папірус Ахмеса, він же папірус Рінда (84 математичні задачі), і московський папірус Голенищева (25 задач), обидва з Середнього царства, часу розквіту давньоєгипетської культури. Автори тексту нам невідомі.
Всі задачі з папірусу Ахмеса (записаний біля 1650 року до н. е.) мають прикладний характер і пов'язані з практикою будівництва, розмежування земельних наділів і т. п. Задачі згруповані не за методами, а за тематикою. Переважно це задачі на знаходження площ трикутника, чотирикутників і круга, різноманітні дії з цілими числами і пропорційний поділ, знаходження відношень, піднесення до різні степенів, визначення середнього арифметичного, арифметичесні прогресії, розв’язання рівнянь першого і другого степеня з одним невідомим.
Повністю відсутні будь-які пояснення або доведення. Шуканий результат або дається прямо, або приводиться короткий алгоритм його обчислення.
Такий спосіб викладу, типовий для науки країн стародавнього Сходу, наводить на роздуми про те, що математика там розвивалася шляхом індуктивних узагальнень і припущень, не створюючи ніякої загальної теорії. Проте, в папірусі є цілий ряд свідчень того, що математика в Давньому Єгипті тих літ мала або принаймні починала набувати теоретичного характеру. Так, єгипетські математики уміли добувати корені і підносити до степеня, розв’язувати рівняння, були знайомі з арифметичною і геометричною прогресією і навіть володіли початками алгебри: при розв’язанні рівнянь спеціальний ієрогліф «купа» позначав невідоме.
В області геометрії єгиптяни знали точні формули для площі прямокутника, трикутника і трапеції. Площа круга обчислювалася, виходячи з припущення П = 3,1605 (похибка менше 1 %).
Єгиптяни знали точні формули для об'єму паралелепіпеда і різних циліндрових тіл, а також піраміди і зрізаної піраміди.
Про більш ранній період розвитку математики в Єгипті відомостей немає ніяких. Про більш пізній, аж до епохи элінізму — теж. Після того, як запанував Птолемей починається надзвичайно плідний синтез єгипетської і грецької культур.
Вавілон
Вавілоняни писали клинописними значками на глиняних табличках, які в чималій кількості дійшли до наших днів (більше 500 тис., з них близько 400 пов'язані з математикою). Тому ми маємо досить повне уявлення про математичні досягнення вчених Вавілонської держави. Зазначимо, що коріння культури вавілонян було в значній мірі успадковане від шумероі — клинописний лист, рахункова методика і т. п.
Вавілонську рахункову техніку набагато краще вивчено ніж египетську, а коло вирішуваних задачі істотно ширше. Є задачі на розв’язування рівнянь другого степеня геометричні прогресії. При розв’язуванні використовувалися, середнє арифметичне, відсотки. Методи роботи з прогресіями глибші, ніж у египтян. Лінійні і квадратні рівняння розв'язувалися ще в епоху Хамурапі; при цьому використовувалася геометрична термінологія (вираз ab називався площею, abc — об'ємом, і т. д.). Багато значків для одночленів були шумерськими, з чого можна зробити висновок про давнину цих алгоритмів; ці значки використовувалися, як буквені позначення невідомих в нашій алгебрі. Зустрічаються також кубичні рівняння і системи лінійних рівнянь. Вінцем планіметрії була теорема Піфагора, відома ще в епоху Хамурапі.
Шумери і вавілоняни використовували 60-кову позиційну систему числення, увіковічнену в нашому поділі круга на 360°, години на 60 хвилин і хвилини на 60 секунд. Для множення використовувався громіздкий комплект таблиць. Для обчислення квадратних коренів вавілоняни винайшли ітераційний процес: нове наближення виходило з попереднього по формулі метода Ньютона: an + 1 = 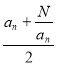
В геометрії розглядалися ті ж фігури, що і в Египті, плюс сегмент круга і зрізаний конус. В ранніх документах вважають П = 3; пізніше зустрічається наближення 25/8 = 3,125. Вавілоняни вміли обчислювати площі правильних многокутників; мабуть, їм був знайомий принцип подібності. Для площі неправильних чотирикутників використовувалася та ж наближена формула, що і в Египті.
Все ж таки багата теоретична основа математики Вавілону не мала цілісного характеру і зводилася до набору розрізнених прийомів, позбавлених доказової бази. Систематичний доказовий підхід в математиці з'явився тільки у греків.
Математика в давньому Китаї
Цифри в стародавньому Китаї позначалися спеціальними ієрогліфами, які з'явилися в II тисячолітті до н. э., і зображення їх остаточно сформувалось до III століття до н. э. Ці ієрогліфи застосовуються і в даний час. Китайський спосіб запису чисел спочатку був мультиплікативним. Наприклад, запис числа 1946, використовуючи замість ієрогліфів римські цифри, можна умовно представити як 1М9С4Х6. Проте на практиці розрахунки виконувалися на рахунковій дошці, де запис чисел був іншим — позиційної, як в Індії, і, на відміну від вавілонян, десяткової.
Обчислення проводилися на спеціальній рахунковій дошці суаньпань, за принципом користування аналогічної російській рахівниці. Нуль спочатку позначався порожнім місцем, спеціальний ієрогліф з'явився близько XII століття н. э. Для запам'ятовування таблиці множення існувала спеціальна пісня, яку учні заучували напам'ять.
Найзмістовніший математичний твір стародавнього Китаю — «Математика в дев’яти книгах».
Китайцям було відоме багато чого, у тому числі: вся базова арифметика (включаючи знаходження найбільшого спільного дільника і найменшого спільного кратного), дії з дробами, пропорції, від’ємні числа, площі і об'єми основних фігур і тіл, теорема Піфагора і алгоритм підбору піфагорових трійок, розв’язання квадратних рівнянь. Був навіть розроблений метод фан-чэн для розв’язання систем довільного числа лінійних рівнянь — аналог класичного європейського методу Гауса. Чисельно розв'язувалися рівняння будь-якого степеня — способом тянь-юань, що нагадує метод Руффіні-Горнера для знаходження коренів многочлена.
Стародавня Греція
Математика в сучасному розумінні цього слова народилася в Греції. В країнах-сучасниках Еллади математика використовувалася або для щоденних потреб (підрахунки, вимірювання), або, навпаки, для магічних ритуалів, що мали на меті з'ясувати волю богів. Математичної теорії в повному розумінні цього слова не було, робота обмежувалася зведенням до емпіричних правил, часто неточних або навіть помилкових.
Греки підійшли до справи з другого боку.
По-перше піфагорійська школа висунула тезу «Числа керують світом». Або, як сформулювали цю ж думку два тисячоліття опісля: «Природа розмовляє з нами на мові математики» (Галілей). Це означало, що істини математики є у відомому значенні істини реального буття.
По-друге, для відкриття таких істин піфагорійці розробили закінчену методологію. Спочатку вони склали список первинних, інтуїтивно очевидних математичних істин (аксіоми, постулати). Потім за допомогою логічних міркувань (правила яких також поступово уніфікувалися) з цих істин виводилися нові твердження, які також зобов'язані бути істинними. Так з'явилася дедуктивна математика.
Греки перевірили справедливість цієї тези в багатьох галузях: астрономія, оптика, музика, геометрія, пізніше — механіка. Усюди були відзначені вражаючі успіхи: математична модель володіла незаперечною пророкуючою силою.
Спроба піфагорійців покласти в основу світової гармонії цілі числа (і їх відношення) була поставлена під сумнів після того, як були знайдені ірраціональні числа. Платонівська школа (IV ст.. до н. е.) вибрала інший, геометричну основу математики (Евдокс Книдський). На цьому шляху були досягнуті найбільші успіхи античної математики (Евклід, Архімед, Аполоній Пергський і інші).
Грецька математика вражає перш за все багатством змісту. Багато учених Нового часу відзначали, що мотиви своїх відкриттів черпнули у стародавніх. Початки аналізу помітні у Архімеда, корені алгебри — у Діофанта, аналітична геометрія — у Аполлонія і т. д. Але головне не в цьому. Два досягнення грецької математики далеко пережили своїх творців.
Перше — греки побудували математику як цілісну науку з власною методологією, заснованою на чітко сформульованих законах логіки (гарантуючих істинність висновків за умови, що істинні передумови).
Друге — вони проголосили, що закони природи зрозумілі для людського розуму, і математичні моделі — ключ до їх пізнання.
В цих двох узагальненнях старогрецька математика цілком споріднена сучасній.
Індійська нумерація (спосіб запису чисел) спочатку була вишуканою. В санскриті були знаки для запису чисел до 1050. Для цифр спочатку використовувалася система Сиро-Фінікії, а з VI століття до н. е. — написання «брахми», з окремими знаками для цифр 1-9. Дещо видозмінившись, ці значки сталі сучасними цифрами, які ми називаємо арабськими, а самі араби — індійськими.
Біля 500 року н. е. невідомий нам великий індійський математик винайшов нову систему запису чисел — десяткову позиційну систему. В ній виконання арифметичних дій виявилося набагато простіше, ніж в старих, з незграбними буквеними кодами, як у греків, або шестидесяткових, як у вавілонян. Надалі індійці використовували рахункові дошки, пристосовані до позиційного запису. Вони розробили повні алгоритми всіх арифметичних операцій, включаючи добування квадратних і кубічних коренів.
До V—VI століть відносяться праці Аріабхати, видатного індійського математика і астронома. В його праці «Аріабхатіам» зустрічається безліч розв’язань розрахункових задач. В VII столітті працював інший відомий індійський математик і астроном Брахмагупта. Починаючи з Брахмагупти, індійські математики вільно поводяться з від’ємними числами, потрактувавши їх як борг.
Найбільшого успіху середньовічні індійські математики досягли в області теорії чисел і числових методів. Індійці далеко просунулися в алгебрі; їх символіка багатша, ніж у Діофанта, хоча дещо громіздка (засмічена словами). Геометрія викликала у індійців менший інтерес. Дведення теорем складалися з креслення і слова «дивися». Формули для площ і об'ємів, а також тригонометрію вони, швидше за все, успадковували від греків.
Математика ісламського середньовіччя
Математика Сходу, на відміну від грецької, завжди носила більш практичний характер. Відповідно найбільше значення мали обчислювальні і вимірювальні аспекти. Основними областями застосування математики були торгівля, будівництво, географія, астрономія і астрологія, механіка, оптика.
В IX ст. жив і — син зороастрійського жерця, якого назвали за це аль-Маджусі (маг). Вивчивши індійські і грецькі знання, він написав книгу «Про індійський рахунок», сприяючий популяризації позиційної системи у всьому Халіфаті, аж до Іспанії. В XII столітті ця книга перекладається на латинську, від імені її автора походить наше слово «алгоритм» (вперше в наближеному значенні використано Лейбнецем). Інший твір ал-Хорезмі «Коротка книжка про обчислення аль-джабра і аль-мукабали», зробив великий вплив на європейську науку і породив ще один сучасний термін «алгебра».
Ісламські математики приділяли багато уваги не тільки алгебрі, але також геометрії і тригонометрії (в основному для астрономічних обчислень). Насир ад-Дін ат-Тусі (ст..) і Ал-Каші (XV ст..) опублікували відомі роботи в цих областях.
В цілому можна сказати, що математикам країн ісламу у ряді випадків вдалося підняти напівемпіричні індійські розробки на високий теоретичний рівень і тим самим розширити їх потужність. Хоча цим синтезом справа в більшості випадків і обмежилася. Багато математиків віртуозно володіли класичними методами, проте нових результатів отримано небагато.
Середньовіччя, IV—XV століття
В V столітті настав кінець Західної Римської імперії, і територія Західної Європи надовго опинилася в полі нескінченних битв із завойовниками і розбійниками (гунни, готи, венгри, и, нормани і т. п.). Розвиток науки припинився. Потреба в математиці обмежується арифметикою і розрахунком календаря церковних свят, причому арифметика вивчається за стародавнім підручником Нікомаха Геразського в скороченому перекладі Боеція на латинськиу.
Серед небагатьох високоосвічених людей можна відзначити ірландця Бемду Достопочтенного (він займався календарем пасхаліями, хронологією, теорією рахунку на пальцях) і ченця Герберта, з 999 року — римського папу під ім'ям Сильвестр II, покровителя наук; йому приписують авторство декількох праць по астрономії і математиці.
Стабілізація і відновлення європейської культури починається з XI ст. З'являються перші університети (Салерно, Болонья). Розширюється викладання математики: в традиційний квадривіум входили арифметика, геометрія, астрономія і музика.
Перше знайомство європейських учених з античними відкриттями відбувалося в Іспанії. В XII ст.. там перекладаються (з грецької і арабської на латинську) основні праці великих греків і їх ісламських учнів. З XIV ст.. головним місцем наукового обміну стає Візантія. Особливо охоче перекладалися і видавалися «Начала» Евкліда; поступово вони обростали коментарями місцевих геометрів.
В кінці XII століття на базі декількох монастирських шкіл був створений Парижський університет, де навчалися тисячі студентів зі всіх кінців Європи; майже одночасно виникають Оксфорд і Кембридж в Британії. Інтерес до науки росте, і один з проявів цього — зміна числової системи. Довгий час в Європі застосовувалися римські цифри. В XII—XIII століттях публікуються перші в Європі праці по десятковій позиційній системі запису чисел (спочатку переклади і, потім власне керівництво), і починається її застосування. З XIV століття індо-арабські цифри починають витісняти римські навіть на могильних плитах. Тільки в астрономії ще довго застосовувалася шестидесяткова вавілонська арифметика.
Першим відомим математиком середньовічної Європи став в XIII ст.. Леонардо Пізанській, відомий під прізвиськом Фібоначчі. Основна його праця: «Книга абака» (1202 рік, друге перероблене видання — 1228 рік). Абаком Леонардо називав арифметичні обчислення. Фібоначчі був добре знайомий (за арабськими перекладами) досягнень стародавніх і систематизував значну їх частину в своїй книзі. Його виклад по повноті і глибині відразу став вищим за всі античні і ісламські прототипи, і довгий час був неперевершеним. Ця книга зробила величезний вплив на розповсюдження математичних знань, популярність індійських цифр і десяткової системи в Європі.
В книжках «Арифметика» і «Про дані числа» Іордана Неморарія вбачаються зачатки символічної алгебри, що до певного часу не відділилася від геометрії.
В цей же час Роберт Гросетест і Роджер Бекон закликають до створення експериментальної науки, яка на математичній мові зможе описати природні явища.
В XIV столітті університети з'являються майже у всіх великих містах (Прага, Краків, Вєна, Гейдельберг, Лейпціг, Базель і ін.).
Філософи з Оксфордського Мертон-коледжу, що жили в XIV столітті і що входили до групи так званих оксфордських калькуляторів, розвивали логіко-математичне вчення про посилення і ослаблення якостей. Інший варіант цього ж вчення розвивав в Сорбонні Миколай Орем. Він ввів зображення залежності за допомогою графіка, досліджував збіжність рядів. В працях по алгебрі він розглядав дробові показники степенів.
Відомий німецький математик і астроном XV ст.. Іоганн Мюллер став широко відомий під ім'ям Регіонмонтан — латинізованою назвою його рідного міста Кенігсберг. Він надрукував першу в Європі працю, спеціально присвячений тригонометрії. В порівнянні з арабськими джерелами новою, але треба особливо відзначити систематичність і повноту викладу.
Лука Пачолі, найбільший алгебрист XV століття, друг Леонардо да Вінчі, подав зрозумілий (хоч не дуже зручний) нарис символіки алгебри.
XVI століття
XVI ст.. стало переломним для європейської математики. Повністю засвоївши досягнення попередників, вона декількома могутніми ривками вирвалася далеко уперед.
Першим великим досягненням стало відкриття загального методу розв’язання рівнянь третього і четвертого степеня. Італійські математики дель Ферро, Тарталья і Феррарі розв'язали проблему, з якою декілька століть не могли справитися кращі математики світу. При цьому виявилося, що в розв’язанні іноді з'являлися «неможливі корені» з від’ємних чисел. Після аналізу ситуації європейські математики назвали ці корені «уявними числами» і винайшли правила поводження з ними, що приводять до правильного результату. Так в математику вперше ввійшли комплексні числа.
Найважливіший крок до нової математики зробив француз Франсуа Вієт. Він остаточно сформулював символічну метамову арифметики — буквену алгебру. З її появою відкрилася можливість проведення досліджень небаченої раніше глибини і спільності. В своїй книзі «Введення в аналітичне мистецтво» Вієт показав приклади потужності нового методу, знайшовши знамениті формули Вієта. Символіка Вієта ще не була схожа на прийняту нині, сучасний її варіант пізніше запропонував Декарт.
Третє велике відкриття XVI століття — винахід логарифмів. Складні розрахунки спростилися у багато разів, а математика отримала нову некласичну функцію з широкою областю застосування.
В 1585 році фламандець Симон Стевін видає книгу «Десята» про правила дій з десятковими дробами, після чого десяткова система бере остаточну перемогу і в області дробових чисел. Стевін також проголосив повну рівноправність раціональних і ірраціональних чисел, а також (з деякими обмовками) і від’ємних чисел.
Одночасно росте престиж математики, удосталь з'являється безліч практичних задач, що вимагають рішення — в артилерії, мореплаванні, будівництві, промисловості, гідравліці, астрономії, картографії, оптиці і ін. І, на відміну від античності, вчені Відродження не цуралися таких задач. Чистих математиків-теоретиків фактично не було. З'являються перші Академії наук. В XVI—XVII століттях роль університетської науки падає, з'являється безліч учених-непрофесіоналів: Стевін — військовий інженер, Вієт і Ферма — юристи Дезарг і Рен — архітектори Лейбніц — урядовець, Непер, Декарт Паскаль — приватні особи.
XVII століття
В XVII ст.. швидкий розвиток математики продовжується, і до кінця століття вигляд науки корінним чином міняється.
Рене Декарт виправляє стратегічну помилку античних математиків і відновлює розуміння алгебри числа (замість геометричного). Більш того, він указує спосіб перекладу геометричних пропозицій на мову алгебри (з допомогою системи координат), після чого дослідження стає набагато ефективно. Так народилася аналітична геометрія. Декарт розглянув безліч прикладів, що ілюструють величезну потужність нового методу, і отримав чимало результатів, невідомих стародавнім. Особливо слід зазначити розроблену їм математичну символіку, близьку до сучасної.
Аналітичний метод Декарта негайно узяли на озброєння Валіс, Ферма і багато інших відомих математиків.
Пьєр Ферма Гюйгенс і Якоб Бернуллі відкривають новий розділ математики, якому призначено велике майбутнє — теорію ймовірності. Якоб Бернуллі формулює першу версію закону великих чисел.
І, нарешті, з'являється не дуже чітка, але глибока ідея — аналіз довільних кривих за допомогою розкладання їх на нескінченно малі відрізки прямих. Першою реалізацією цієї ідеї був багато в чому недосконалий метод неподільних, і вже з його допомогою було зроблено безліч нових відкриттів. В кінці XVII століття ідея неподільних була істотно розширена Ньютоном і Лейбніцом, і з'явився виключно могутній інструмент дослідження — математичний аналіз. Цей математичний напрям став основним в наступному XVIII ст..
Теорія від’ємних чисел все ще знаходилася у стадії становлення. Жваво обговорювалася, наприклад, дивна пропорція 1 : (-1) = (-1) : 1 — в ній перший член зліва більший від другого, а справа — навпаки, і виходить, що більше рівно меншому («парадокс Арно»).
Комплексні числа вважалися фіктивними, правила дій з ними не були остаточно відпрацьовані. Більш того, було незрозуміло, чи все «уявні числа» можна записати у вигляді a + bi або, скажімо, при добуванні деякого кореня можуть з'явитися уявності, що не зводяться до цієї форми (так вважав навіть Лейбніц). Тільки в XVIII столітті Даламбер і Ейлер встановили, що комплексні числа замкнуті щодо всіх операцій, включаючи добування кореня будь-якого степеня.
В другій половині XVII століття з'являється наукова періодика, ще не спеціалізована по видах наук. Початок поклали Лондон і Париж, але особливо важливу роль зіграв журнал Acta Eruditorum (1682, Лейпціг, на латинській мові). Французська Академія наук видає свої записки (Memoires) з 1699 року. Виходили ці журнали рідко, і листування продовжувало залишатися незамінним засобом розповсюдження інформації.
XVIII століття
XVIII ст.. в математиці можна стисло охарактеризувати як століття аналізу, який став головним об'єктом доповнення зусиль математиків. Сприяючи бурхливому розвитку природних наук, аналіз, у свою чергу, прогресував сам, одержуючи від них все більш і більш складні задачі. На стику цього обміну ідеями народилася математична фізика.
Критика методу нескінченно малих за погану обгрунтованість швидко замовкла під тиском тріумфальних успіхів нового підходу. В науці, дякуючи Ньютону, панувала механіка — всі інші взаємодії вважалися вторинними, слідствами механічних процесів. Розвиток аналізу і механіки відбувалися в тісному переплетенні; першим це об'єднання здійснив Ейлер, який видалив з ньютонівської механіки архаїчні конструкції і підвів під динаміку аналітичний фундамент (1736). З цієї миті механіка стала прикладним розділом аналізу. Процес завершив Лагранж, чия «Аналітична механіка» демонстративно не містить жодного креслення. Одночасно аналіз алгебраїзувався і остаточно (починаючи з Ейлера) відділився від геометрії і механіки.
Головним методом пізнання природи стає складання і розв’язання диференціальних рівнянь. Потім настає черга динаміки твердого тіла, потім — рідини і газу.
Теорія тяжіння Ньютона спочатку зустрічала з труднощами під час опису руху Місяця, проте роботи Клеро, Ейлера і Лапласа ясно показали, що ніяких додаткових сил, окрім ньютонівських, в небесній механіці неіснує.
Аналіз розповсюджується на комплексну область. Аналітиче дослідження більшості функцій проблем не викликало, і були знайдені несподівані зв'язки між стандартними функціями (формула Ейлера). Труднощі зустрілися для комплексного логарифму, але Ейлер їх успішно подолав. Були введені конформні відображення, висловлено гіпотезу про єдиність аналітичного доповнення. Комплексні функції знайшли навіть застосування в прикладних науках — гідродинаміці, теорії коливань (Даламбер, Ейлер).
Далеко пішли вперед теорія і техніка інтегрування. Входять в широке вживання кратні інтеграли (Ейлер, Лагранж), причому не тільки в декартових координатах. Посилено вивчається теорія диференціальних рівнянь, як загальних, так і в часткових похідних. Математики проявляють виняткову винахідливість при розв’язанні диференціальних рівнянь в часткових похідних, для кожної задачі знаходивши свої методи розв’язання.
В кінці XVIII століття було започато загальну теорію потенціала (Лагранж, Лаплас, Лежандр). Для тяжіння потенціал ввів Лагранж (1773, термін запропонував Грін в 1828 році). Незабаром Лаплас знайшов зв'язок потенціалу з рівнянням Лапласа і ввів важливий тип ортогональних сферичних функцій.
Виникають багатообіцяюче варіаційне численння і варіаційні принципи фізики (Ейлер, Лагранж).
Лідером математиків XVIII століття був Ейлер, чий винятковий талант наклав відбиток на все основні математичні досягнення сторіччя. Саме він зробив з аналізу досконалий інструмент дослідження. Ейлер істотно збагатив різновид функцій, розробив техніку інтеграції, далеко просунув практично всі області математики. Наряду з Мопертюї він сформулював принцип найменшої дії як вищий і універсальний закон природи.
В теорії чисел остаточно легалізували уявні числа, хоча повна теорія їх ще не створена. Доведена (ще не цілком строго) основна теорема алгебри. Ейлер розробив теорію подільності цілих чисел і теорію порівнянь (вирахувань), завершену Гаусом. Ейлер ввів поняття первісного кореня, довів його існування для будь-кого простого числа і знайшов кількість первісних коренів. Він і Лагранж опублікували загальну теорію ланцюгових дробів, і з їх допомогою розв’язали немало задач діофантового аналізу. Ейлер також знайшов, що у ряді задач теорії чисел можна застосувати аналітичні методи.
Стрімко розвивається лінійна алгебра. Перший опис загального розв’язання лінійних систем описав в 1750 році Габриель Крамер. Близьку до сучасної символіку і глибокий аналіз визначників виклав Олександр Теофіл Вандермонд (1735—1796). Лаплас в 1772 році дав розкладання визначника по мінорам. Теорія визначників швидко знайшла безліч застосувань в астрономії і механіці (вікове рівняння), при рішенні систем алгебри, дослідженні форм і т. д.
В алгебрі назрівають нові ідеї, що завершилися вже в XIX столітті теорією Галуа і абстрактними структурами. Лагранж при дослідженні рівнянь п'ятого степеня і підходить до теорії Галуа (1770), з'ясувавши, що «істинна метафізика рівнянь — теорія підстановок».
В геометрії з'являються нові розділи: диференціальна геометрія кривих і поверхонь нарисна геометрія (Монж), проективна геометрія (Лазар Карно).
Теорія ймовірності перестає бути екзотикою і доводить свою корисність в найнесподіваніших областях людської діяльності. Де Муавр і Даниїл Бернуллі відкривають нормальний расподіл. Виникають теорія вірогідності помилок і наукова статистика. Класичний етап розвитку теорії вірогідності завершили роботи Лапласа. Проте додатки її до фізики тоді ще майже були відсутні (не рахуючи теорії помилок).
Центрами математичних досліджень стають Академії наук, здебільшого державні. Значення університетів невелике (виключаючи країни, де академій ще немає), фізико-математичні факультети все ще відсутні. Провідну роль відіграє Парижська академія. Англійська школа після Ньютона відоособлюється і на ціле століття знижує науковий рівень; число відомих математиків в Англії XVIII століття невелике — де Муавр (французький емігрант-гугенот) Котс, Тейлор, Маклорен, Стирлінг.
Математики стають професіоналами, любителі майже зникають з сцени.
В кінці XVIII століття з'являються спеціалізовані математичні журнали, збільшується інтерес до історії науки. Виходить двотомна «Історія математики» Монтюкла (посмертно перевидана і доповнена до 4 томів). Розширюється видання науково-популярної літератури.
XIX століття
Незаперечна ефективність застосування математики в природознавстві підштовхувала учених до думки, що математика, так би мовити, вбудована у всесвіт, є його ідеальною основою. Іншими словами, пізнання в математиці є частина пізнання реального світу. Багато учених XVII—XVIII століть в цьому і не сумнівалися. Але в XIX столітті еволюційний розвиток математики був порушений, цей, що здавався непохитним, теза була поставлена під сумнів.
Неевклідова геометрія
В геометрії, алгебрі, аналізі з'являються численні нестандартні структури з незвичайними властивостями: неевклідова і багатовимірна геометрія кватерніони, скінченні поля, некомутативні группи і т. п.
Об'єктами математичного дослідження все більше стають нечислові об'єкти: події, предикати, множини, абстрактні структури вектори, тензори, матриці, функції, багатолінійні форми і т. д.
Виникає і одержує широкий розвиток математична логіка, у зв'язку з чим з'явилася спокуса пов'язати саме з нею основу математики.
Георг Кантор вводить в математику гранично абстрактну теорію множин, а заразом поняття актуальної нескінченності довільного масштабу. В кінці століття при спробі обгрунтувати фундамент математики на основі теорії множин були знайдені суперечності, які примусили задуматися над непростими питаннями: що означає «існування» і «істинність» в математиці?
В цілому в XIX столітті роль і престиж математики в науці і економіці помітно ростуть. Відповідно росте і її державна підтримка. Математика знов стає по перевазі університетською наукою. З'являються перші математичні суспільства: Лондонське, Американське, Французське, Московське, а також об’єднання в Палермо і Единбурзі.
Розглянемо коротко розвиток основних областей математики в XIX столітті.
Геометрія
Якщо XVIII століття було століттям аналізу, то XIX століття по перевазі стало століттям геометрії. Швидко розвиваються створені в кінці XVIII століття нарисна геометрія (Монж, Ламберт) і відроджена проективна геометрія (Монж Понселе, Лазар Карно). З'являються нові розділи: векторне числення и векторний анализ, геометрия Лобачевского, багатовимірна ріманова геометрія, теорія груп преотворень. Відбувається інтенсивна алгебраїзація геометрії — в неї проникають методи теорії груп, в кінці століття — топологія, виникає алгебраїчна геометрія.
Диференціальна геометрія отримала могутній поштовх після виходу надзвичайно змістовної праці Гауса «Загальні дослідження про криві поверхні» (1822), де вперше були явно визначені метрика (перша квадратична форма) і пов'язана з нею внутрішня геометрія поверхні. Дослідження продовжила паризька школа. В 1847 році Френе і Серре опублікували відомі формули Френе для диференціальних атрибутів кривої.
Найбільшим досягненням стало введення поняття вектора і векторного поля. Спочатку вектори ввів У. Гамільтон у зв'язку з своїми кватерніонами (як їх тривимірну уявну частину). У Гамільтона вже з'явився скалярний і векторний добуток. Понад те, Гамільтон ввів диференціальний оператор («набла») і багато інших понять векторного аналізу, у тому числі визначення вектор-функції і добутку.
Компактність і інваріантність векторної символіки, використаної в перших працях Максвела, зацікавили фізиків; незабаром вийшли «Елементи векторного аналізу» Гіббса (1880-і роки), а потім Хевісайд (1903) додав векторному численню сучасний вигляд.
Проективна геометрія після півтора століть забуття знов привернула увагу — спочатку Монжа, потім його учнів — Понселе і Лазара Карно. Карно сформулював «принцип безперервності», який дозволяє відразу розповсюдити деякі властивості початкової фігури на фігури, отримані з неї безперервним перетворенням (1801—1806). Дещо пізніше Понселе ясно визначив проективну геометрію як науку про проективні властивості фігур і дав систематичний виклад її змісту (1815). У Понселе вже повністю легалізовані нескінченно видалені точки (навіть уявні).
З кінця 1820-х років формується школа проективних геометрів в Німеччині (Мебіус, Плюккер, Гессе, Штейнер і інші). В Англії ряд робіт опублікував Кели. При цьому стали використовуватися і аналітичні методи, особливо після відкриття Мебіусом однорідних проективних координат, включаючи і нескінченно видалену точку. У Франції роботи Понселе продовжив Мішель Шаль.
Великий вплив на розвиток математики мала знаменита мова Рімана (1854) «Про гіпотези, що лежать в підставі геометрії». Ріман визначив загальне поняття n-вимірного образу і його метрику у вигляді довільної позитивно визначеної квадратичної форми. Далі Ріман узагальнив теорію поверхонь Гауса на багатовимірний випадок; при цьому з'являються знаменитий ріманів тензор кривизни і інші поняття рімановой геометрії. Існування неевклидової метрики, за Ріманом, може пояснюватися або дискретністю простору, або якимись фізичними силами зв'язку. В кінці століття Г. Річчі завершує класичний тензорний аналіз.
В другій половині XIX століття нарешті привертає загальну увагу геометрія Лобачевського. Той факт, що навіть у класичної геометрії існує альтернатива, справив величезне враження на весь науковий світ. Він також стимулював переоцінку багатьох стереотипів, що встановились, в математиці і фізиці.
Ще один переломний момент розвитку геометрії наступив в 1872 році, коли Фелікс Клейн виступив з своєю «Ерлангенською програмою». Він класифікував геометричні науки за групами перетворень , що використовуються, — обертання, афінні, проективні, загальні безперервні і т. п. Кожний розділ геометрії вивчає інваріанти відповідної групи перетворень. Клейн розглянув також найважливіше поняття ізоморфізму (структурної тотожності), який називав «перенесенням». Тим самим був намічений новий етап алгебраїзації геометрії, другої після Декарта.
В 1872—1875 роках Каміл Жордан опублікував ряд робіт по аналітичній геометрії n-вимірного простору (кривих і поверхонь), а в кінці століття він запропонував загальну теорію.
В самому кінці століття народжується топологія, спочатку під назвою analysis situs. Топологічні методи фактично у ряді робіт використовували Ейлер, Гаус, Ріман, Жордан і ін. Цілком явно предмет нової науки описує Фелікс Клейн в своїй «Ерлангенській програмі». Грунтовно комбінаторна топологія оформилася в роботах Пуанкаре (1895—1902).
Математичний аналіз
Аналіз в XIX столітті розвивався шляхом швидкої, але мирної еволюції.
Найістотнішою зміною стало створення фундаменту аналізу (Коші, потім Вейерштрасса). Дякуючи Коші містичне поняття актуального нескінченно малого зникло з математики (хоча у фізиці воно використовується дотепер). Були поставлені під сумнів дії з рядами, що розходяться. Коші побудував фундамент аналізу на основі теорії границь, близької до ньютонівського розуміння, і його підхід став загальноприйнятим; аналіз став менш алгебраїчним, але більш надійним. Проте до уточнень Вейерштрасса багато забобонів ще зберігалися: наприклад, Коші вірив, що безперервна функція завжди диференціальна, а сума ряду з безперервних функцій безперервна.
Широкий розвиток отримала теорія аналітичних функцій комплексного змінного, над якою працювали Лаплас, Коші Абель, Ліувіль, Якобі, Вейерштрасс і інші. Значно розширився сам клас спеціальних функцій, особливо комплексних. Головні зусилля були направлені на теорію абелевих функцій, які не цілком виправдали покладені на них надії, але сприяли збагаченню аналітичного інструментарію і створенню в XX столітті більш загальних теорій.
Численні прикладні задачі діяльно стимулювали теорію диференціальних рівнянь, що переросла в опотужну і плідну математичну дисципліну.
До кінця століття відбувається деяка геометризація аналізу — з'являються векторний аналіз, тензорний аналіз, досліджується нескінченновимірні функціональні простори (Банаховий простір, Гільбертовий простір). Компактний інваріантний запис диференціальних рівнянь набагато зручніший і наочніший, ніж громіздкий координатний запис.
Алгебра і теорія чисел
Намічені у Ейлера аналітичні методи допомогли розв'язати чимало важких проблем теорії чисел (Гаус, Діріхле і інші). Гаус дав перший бездоганний доказ основної теореми алгебри. Жозеф Ліувіль довів існування нескінченної кількості трансцендентних чисел (1844, докладніше в 1851), дав достатню ознаку трансцендентності і побудував приклади таких чисел у вигляді суми ряду. В 1873 році Шарль Ерміт публікує доказ трансцендентної числа Ейлера e, а в 1882 році Ліндеман застосував аналогічний метод і до числа П.
У. Гамільтон відкрив дивний некомутативний світ кватерніонів.
Виникла геометрична теорія чисел (Мінковський).
Еваріст Галуа, що випередив свій час, представив глибокий аналіз розв’язання рівнянь довільних степенів. Ключовими поняттями дослідження виявляються властивості алгебри пов'язаних з рівнянням групи підстановок і полів розширення. Галуа завершив роботи Абеля, що довів, що рівняння ступеня вище 4-й нерозв’язні в радикалах.
У міру засвоєння ідей Галуа, з другої половини століття, швидко розвивається абстрактна алгебра. Жозеф Ліувілль публікує і коментує роботи Галуа. В 1850-і роки Кели вводить поняття абстрактної группи. Термін «група» стає загальноприйнятим і проникає практично у всі області математики, а в XX столітті — у фізику і кристалографію.
Формується поняття лінійного простору (Грасман і Келі 1843—1844). В 1858 році Келі публікує загальну теорію матриць, визначає операції над ними. До 1870 року доведені всі базові теореми лінійної алгебри, включаючи зведення до жорданової нормальної форми.
В 1871 році Дедекінд вводить поняття кільца, модуля і ідеала. Він і Кронекер створюють загальну теорію подільності.
В кінці XIX століття в математику входять групи Ли.
Теорія ймовірності
На перше місце виходять теорія помилок, статистика і фізичні додатки. Цим займалися Гаус, Пуассон, Коші. Була виявлена важливість нормального розподілу як граничного в багатьох реальних ситуаціях.
У всіх розвинутих країнах виникають статистичні департаменти/суспільства. Завдяки роботам Карла Пірсона виникає математична статистика з перевіркою гіпотез і оцінкою параметрів.
Все ж таки математичні основи теорії ймовірності в XIX столітті ще не були створені, і Гільберт на початку XX століття відніс цю дисципліну до прикладної фізики.
Математична логіка
Після невдачі проекту «Універсальної характеристики» Лейбніца пройшло півтора століття, перш ніж спроба створити алгебру логіки повторилася. Але повторилася вона на новій основі: концепція безлічі істинності дозволила побудувати математичну логіку як теорію класів, з теоретико-множинними операціями. Піонерами сталі британські математики Август (Огюстес) де Морган і Джордж Буль.
В роботі «Формальна логіка» (1847) де Морган описав поняття універсуму і символи для логічних операторів, записав відомі «закони де Моргана». Пізніше він ввів загальне поняття математичного відношення і операцій над відношеннями.
Джордж Буль незалежно розробив свій, більш вдалий, варіант теорії. В своїх роботах 1847—1854 років він заклав основи сучасної математичної логіки і описав алгебру логіки (булеву алгебру). З'явилися перші логічні рівняння, введено поняття розкладання логічної формули.
Уільям Стенлі Джевонс продовжив систему Буля і навіть побудував «логічну машину», здатну вирішувати логічні задачі. В 1877 році Ернест Шредер сформулював логічний принцип подвійності. Далі Готлоб Фреге побудував обчислення висловлювань. Чарльз Пірс в кінці XIX століття виклав загальну теорію відносин і пропозиційних функцій, а також ввів квантори. Сучасний варіант символіки запропонував. Після цього все було готово для розробки в школі Гільберта теорії доведень.
Обгрунтовування математики
До початку XIX століття відносно строге логічне (дедуктивне) обгрунтування мала тільки евклідова геометрія, хоча строгість її вже тоді справедливо вважалася недостатньою. Властивості нових об'єктів (наприклад комплексних чисел, нескінченно малих і т. д.) просто вважалися в цілому такими ж, як у об'єктів вже відомих; якщо ж така екстраполяція була неможлива, властивості підбиралися досвідченим шляхом.
Побудова фундаменту математики почалася з аналізу. В 1821 році Коші опублікував «аналіз Алгебри», де чітко визначив основні поняття на основі концепції границь. Все ж таки він зробив ряд помилок, наприклад, почленно інтегрував і диференціював ряди, не доводячи допустимість таких операцій. Завершив фундамент аналізу Вейєрштрасс, який з'ясував роль важливого поняття рівномірної неперервності. Одночасно Вейерштрасс (1860-і роки) і Дедекінд (1870-і) дали обгрунтовування теорії чисел.
1837 рік: Уільям Гамільтон будує модель комплексних чисел як пара речовинних.
В 1870-і роки були легалізовані неевклидові геометрії. Їх моделі на базі евклідового простору довели, що вони так само несуперечливі, як і геометрія Евкліда.
1879 рік: Фреге публікує систему аксіом математичної логіки.
1888 рік: Дедекінд пропонує нарис системи аксіом для натуральних чисел. Роком пізніше закінчену систему аксіом запропонував.
1899 рік: виходять в світ «Підстави геометрії» Гільберта.
У результаті до кінця століття майже вся математика була побудована на базі строгої аксіоматики. Несуперечливість основних розділів математики (окрім арифметики) була строго доведена (точніше кажучи, зведена до несуперечності арифметики). Аксіоматичний фундамент для теорії ймовірності і теорії множин з'явився пізніше, в XX столітті.
Теорія множин і антиномії
В 1873 році Георг Кантор ввів поняття довільної числової множини, а потім і загальне поняття множини — найабстрактнішого поняття в математиці. З допомогою взаємно-однозначних відтворень він ввів поняття рівно потужності множин, потім визначив порівняння потужностей на більшо-менший і, нарешті, класифікував множини по величині їх потужності.
Ієрархію потужностей Кантор розглядав як продовження ієрархії (порядку) цілих чисел. Тим самим в математику була введена актуальна нескінченність — поняття, якого колишні математики старанно уникали.
На перших порах теорія множин зустріла у багатьох математиків доброзичливий прийом. Вона допомогла узагальнити жорданівську теорію мір, успішно використовувалася в теорії інтегралу Лебега і багато ким розглядалася як основа майбутньої аксіоматики всієї математики. Проте наступні події показали, що звична логіка не годиться при дослідженні нескінченності, а інтуїція не завжди допомагає зробити правильний вибір.
Перша суперечність виявилася при розгляді найбільшої множини — безліч всіх множин (1895). Його довелося виключити з математики як недопустиме. Проте з'явилися і інші суперечності (антиномії).
Анрі Пуанкаре, який спочатку прийняв теорію множин і навіть використав в своїх дослідженнях, пізніше рішуче відкинув її і назвав «важкою хворобою математики». Проте інша група математиків, включаючи Бертрана Рассела, Гільберта і Адамара, виступили в захист «канторизму».[
Положення ускладнювало відкриття «аксіомы вибору» (1904, Цермело), яка, виявляється, неусвідомлено застосовувалася в багатьох математичних доведеннях (наприклад, в теорії дійсних чисел). Ця аксіома оголошує існуючою множину, про склад якої ніщо не відоме, і цю обставину ряд математиків порахувало абсолютно неприйнятним, тим більше що деякі наслідки аксіоми вибору суперечили інтуїції (парадокс Банаха — Тарського і ін.).
На початку XX століття вдалося влаштувати варіант теорії множин, вільний від знайдених раніше суперечностей (теорія класів), так що більшість математиків прийняла теорію множин. Проте тої єдності математиків більше неіснувало, частина наукових шкіл стала розвивати альтернативні погляди на обгрунтовування математики.
В 1701 році імператорським указом була відкрита в Сухаревій башні математично-навигаційна школа, де викладав Л. Ф. Магницький. За дорученням Петра I він написав (на церковно-слов'янському) відомий підручник арифметики (1703), а пізніше видавав навігаційні і логарифмічні таблиці. Підручник Магницького для того часу був виключно добротним і змістовним. Автор ретельно відібрав все краще, що було в існуючих тоді підручниках, і виклав матеріал ясно, з численними прикладами і поясненнями.
Могутнім поштовхом до розвитку російської науки послужили реформи М. М. Сперанського. На початку XIX століття було створене Міністерство народної просвіти, почали організовуватись навчальні округи, і гімназії стали відкриватися у всіх великих містах Росії. При цьому зміст курсу математики був досить великим — алгебра, тригонометрія, додатки до фізики і ін.
В XIX ст.. молода російська математика вже мала вчених світового рівня.
Першим з них став Михайло Васильович Остроградський. Як і більшість російських математиків до нього, він розробляв переважно прикладні задачі аналізу. В його працях досліджується розповсюдження тепла хвильове рівняння, теорія пружності, електромагнетизм. Займався також теорією чисел. Академік п'яти світових академій. Важливі прикладні роботи виконав Віктор Якович Буняковський — надзвичайно різносторонній математик, винахідник, визнаний авторитет по теорії чисел і теорії ймовірностей, автор фундаментальної праці «Підстави математичної теорії вірогідності».
Фундаментальними питаннями математики в Росії першої половини XIX століття зайнявся тільки Микола Іванович Лобачевський, який виступив проти догмату евклідовості простору. Він побудував геометрію Лобачевського і глибоко досліджував її незвичайні властивості. Лобачевській настільки випередив свій час, що був оцінений по заслугах тільки через багато років після смерті. Декілька важливих відкриттів загального характеру зробила Софія Ковалевська.
В другій половині XIX століття російська математика, при загальному прикладному нахилі, публікує чимало фундаментальних результатів. Пафнутій Львович Чебишов, математик-універсал, зробив безліч відкриттів в самих різних, далеких один від одного, областях математики — теорії чисел, теорії вірогідності, теорії наближення функцій. Андрій Андрійович Марков відомий першокласними роботами по теорії вірогідності, отримав видатні результати і в інших областях — теорії чисел і математичному аналізі. До кінця XIX століття формуються дві активні вітчизняні математичні школи — московська і петербурзька.
XXстоліття: основні досягнення
Престиж професії математика став в XX сторіччі помітно вище. Математика розвивалася експоненціально, і неможливо скільки-небудь повно перерахувати зроблені відкриття, але деякі найсерйозніші досягнення згадані нижче.
В 1900 році Давид Гільберт на Міжнародному конгресі математиків представив список з 23 нерозв’язаних математичних задач. Ці проблеми охопили безліч областей математики і сформували центр зусиль математиків XX століття. Сьогодні десять проблем із списку вирішено, сім частково вирішені, і дві проблеми все ще відкрито. Що залишилися чотири, сформульовані дуже узагальнено, щоб мало сенс говорити про їх вирішення.
В школі Гільберта з'явився функціональний аналіз, що незабаром знайшов безпосереднє застосування в квантовій фізиці.
На початку століття Эммі Нетер і Ван дер Варден завершили побудову основ абстрактної алгебри, структури якої пронизують всю математику. Лебег і Борель узагальнили жорданову теорію міри; на її основі був побудований інтеграл Лебега.
Загальна топологія стрімко розвивається і знаходить застосування в самих різних областях математики.
Герман Мінковський в 1907 році розгромив геометричну модель кінематики спеціальною теорією відносності, пізніше вона послужила основою для Загальної теорії відносності.
В 1910-х роках Рамануджан сформулював більш ніж 3000 теорем, включаючи властивості функції розкладу числа і її асимптотичних оцінок. Він також отримав важливі результати в області дослідження гама-функції, модулярних форм, розбіжних рядів, гіпергеометричних рядів і теорії простих чисел.
В 1931 році Курт Гедель опублікував дві свої теореми про неповноту, які встановили обмеженість математичної логіки. Це поклало кінець задуму Давида Гільберта створити повну і несуперечливу систему основ математики. Дещо раніше (починаючи з 1915 року) Левенгейм и Сколем знайшли ще один бентежний факт: ніяка аксіоматична система не може бути категорична. Іншими словами, як би ретельно ми не формулювали систему аксіом, завжди знайдеться інтерпретація, абсолютно не схожа на ту, заради якої ця система проектувалася. Ця обставина також підриває віру в універсальність аксіоматичного підходу.
В 1933 році Колмогоров завершив (загальновизнану тепер) аксіоматику теорії ймовірності.
В 1960-х роках Абрахам Робинсон опублікував виклад нестандартного аналізу — альтернативного підходу до обгрунтовування математичесного аналізу на основі актуальних нескінченно малих.
В 1963 році Пол Коен довів, що континіум-гіпотеза Кантора недоказова (в звичайній аксіоматиці теорії множин).
Масовий інтерес викликали фрактали, відкриті Бенуа Мандельбротом (1975).
В другій половині XX століття, у зв'язку з появою комп'ютерів, відбулася істотна переорієнтація математичних зусиль. Значно виросла роль таких розділів, як числові методи, теорія оптимізації, спілкування з дуже великими базами даних, імітація штучного розуму, кодування звукових і відеоданих і т. п. Виникли нові науки — кібернетика і інформатика.
Багато старих проблем отримали вирішення при використанні сучасних методів. Вольфганг Хакен і Кеннет Апель за допомогою комп'ютера вирішили проблему чотирьох кольорів (1976). Эндрю Уайлс, працюючи один в своєму офісі протягом багатьох літ, довів останню теорему Ферма в 1995 році.
Серед найвидатніших математиків XX століття можна назвати (крім вже згаданих) такі імена:
Павло Сергійович Олександров — топологія.
Стефан Банах — функціональний аналіз, теорія множин.
Лейтзен Егберт Ян Брауер — аналіз, топологія, теорія множин філософія математики.
Норберт Вінер — творець кібернетики.
Ізраїль Мойсеєвич Гельфанд — функціональний аналіз, топологія алгебра, математична фізика і ін.
Жан Дьєдоне — функціональний аналіз, топологія алгебраїчна геометрія.
Герман Вейль — алгебра, аналіз, теорія чисел математична логіка, математична фізика і ін.
Анрі Картан — аналіз, топологія.
Джон фон Нейман — математична логіка і теорія комп'ютерів, математична фізика, теорія множин інформатика, економіка, теорія ігр і ін.
Альфред Тарский — математична логіка.
Альфред Норт Уайтхед — математична логіка.
Фелікс Хаусдорф — топологія, теорія множин, функціональний аналіз, теорія чисел.
Олександр Якович Хінчин — теория ймовірності.
Алонзо Черч — інформатика, математична логіка.
Клод Элвуд Шеннон — інформатика, кібернетика.
Ернст Цермело — математична логіка, теорія множин.
Особливий розвиток в XX столітті отримали нові області математики; окрім компьютерних потреб, це пов'язано із запитами теорії керування, квантової фізики і інших прикладних дисциплін.
2. Історія розвитку поняття функції.
Поняття функції має давню історію. Перші кроки на довгому шляху творення загального поняття функції зробили математики Стародавнього Вавилону. Вони склали таблиці обернених значень чисел, їх квадратів і кубів, сум квадратів і кубів чисел. У сучасному розумінні це були таблиці значень функцій у = ![]() , у = х2, у = х3, у = х2 + х3. З їх допомогою можна розв'язувати і обернені задачі. Складали вони і таблиці значень функцій двох змінних, наприклад таблиці додавання та множення.
, у = х2, у = х3, у = х2 + х3. З їх допомогою можна розв'язувати і обернені задачі. Складали вони і таблиці значень функцій двох змінних, наприклад таблиці додавання та множення.
Математики Стародавньої Греції розв'язали деякі задачі на найбільше та найменше значення, відкрили співвідношення між довжинами хорд і діаметрів. Грецькі астрономи заклали основи нової галузі математики — тригонометрії. Вони склали таблиці залежності між довжинами хорд та мірами дуг, що їх стягують. По суті, це вже були таблиці значень функції ![]() . Згодом математики досліджували і багато інших функціональних залежностей. Хоч самого поняття функції не вводили. Навіть у працях Р. Декарта, П. Ферма, І. Ньютона і Г. Лейбніца поняття функції носило по суті інтуїтивний характер і пов'язувалося або з геометричними, або з механічними уявленнями. Шлях до першого означення функції проклав Р. Декарт, ввівши поняття змінної величини.
. Згодом математики досліджували і багато інших функціональних залежностей. Хоч самого поняття функції не вводили. Навіть у працях Р. Декарта, П. Ферма, І. Ньютона і Г. Лейбніца поняття функції носило по суті інтуїтивний характер і пов'язувалося або з геометричними, або з механічними уявленнями. Шлях до першого означення функції проклав Р. Декарт, ввівши поняття змінної величини.
Наприкінці ХVІІ століття Г. Лейбніц та його учні почали застосовувати термін «функція». Спочатку його використовували в дуже вузькому розумінні, пов’язуючи лише з геометричними образами. Йшлося про відрізки дотичних до кривих, їх проекції на осі координат та про інші лінії, які виконують для даної фігури деяку функцію (від латинського «функтус» виконувати). Таким чином, поняття функції ще не було звільнено від геометричної форми.
Лише в 1718 р. Й. Бернуллі (учень і співробітник Г. Лейбніца) сформулював означення функції, вільне від геометричної мови: «Функцією змінної величини називається кількість, утворена яким-завгодно способом з цієї змінної величини і сталих». Відхід від геометричних образів знаменував нову епоху у вивченні функцій. Означення Й. Бернуллі спиралося не лише на роботи Лейбніца та його школи, але й на дослідження І. Ньютона, який вивчив багато різних функціональних залежностей та їх властивостей. Замість слова «функція» І. Ньютон використовував термін «ордината» Він зводив вивчення геометричних та фізичних залежностей до вивчення цих «ординат», а самі «ординати» описував різноманітними аналітичними виразами.
Щоб означення функції, дане Й. Бернуллі, стало повноцінним, потрібно було домовитися, які способи задання функцій можна вважати допустимими. Звичайно, вважали, що допускаються функції, задані виразами, в які входять числа, букви, знаки арифметичних дій, піднесення до степеня з цілим показником та добування коренів, а також позначення тригонометричних, обернених тригонометричних, показникових, логарифмічних функцій, Такі функції називали елементарними. Л. Ейлер у своєму підручнику «Введення в аналіз нескінченних» (1748) дещо уточнив означення Й. Бернуллі: «Коли деякі кількості залежать від інших у такий спосіб, що за зміни останніх і самі вони підлягають зміні, то перші називаються функціями других». В одній із праць він навіть розглядав графік функції як криву, яка накреслена «вільним потягом руки». Праці Л. Ейлера відіграли важливу роль у звільненні математичного аналізу від мови геометрії та механіки. В них вперше теорія тригонометричних функцій була викладена без звернення до геометрії, а показникова та логарифмічна функції стали рівноправними з алгебраїчними. Він наголошував, що математичний аналіз є наука про функції, що «весь аналіз нескінченно малих обертається навколо змінних кількостей та їх функцій».
У зв'язку з таким поглядом Ейлера на функцію між ним та його сучасниками, зокрема французом Ж. Д'Аламбером, виникла полеміка навколо можливості аналітичного вираження довільної кривої і про те, яке із двох означень (крива або формула) слід вважати загальнішим. Виникла також суперечка про те, чи можна одну функцію задавати декількома аналітичними виразами. Роз'яснення вніс французький математик Ж.Фур'є. У поданих ним у Паризьку академію наук у 1807 і 1811 р. мемуарах з теорії розповсюдження тепла в твердому тілі було наведено перші приклади функцій, заданих на різних ділянках різними аналітичними виразами. З праць Ж. Фур'є випливало, що будь-яку криву незалежно від того, із скількох і яких різнорідних частин вона складається, можна подати у вигляді єдиного аналітичного виразу, і що існують також перервні криві, які можна записати аналітичним виразом. Висновки Ж. Фур'є обґрунтував у своїй книзі «Курс алгебраїчного аналізу» (1821) французький математик О. Коші.
М. Лобачевський, розвиваючи ейлерове означення функції, у праці «Про зникання тригонометричних рядків» (1834) писав: «Загальне означення вимагає, щоб функцією від х називати число, яке дається для кожного х і разом з х поступово змінюється. Значення функції може бути дане або аналітичним виразом, або умовою, яка дає засіб випробовувати всі числа і вибирати одне з них; або, нарешті, залежність може існувати і залишатися невідомою ...»
Аналогічну точку зору на поняття функції ще раніше висловив також чеський математик Б. Больцано.
У 1837 р. німецький математик П. Діріхле сформулював таке означення: «у є функцією змінної х(на відрізку a ![]() х
х ![]() b), якщо кожному значенню х (з цього відрізка) відповідає певне значення у, причому не має значення, яким чином встановлена ця відповідність — аналітичною формулою, графіком, таблицею або навіть просто словами».
b), якщо кожному значенню х (з цього відрізка) відповідає певне значення у, причому не має значення, яким чином встановлена ця відповідність — аналітичною формулою, графіком, таблицею або навіть просто словами».
Прикладом, що відповідає цьому загальному означенню, може бути так звана «функція Діріхле»:
![]() 1 для будь-якого раціонального значення х,
1 для будь-якого раціонального значення х,
![]() =
=
0 для будь-якого ірраціонального значення х.
Ця функція задана словесно. Вона відіграє відому роль в аналізі. Аналітично її можна задати лише за допомогою досить складної формули.
Отже, приблизно в середині XIX ст. після довготривалої боротьби думок поняття функції звільнилося від аналітичного виразу чи математичної формули. Головний акцент в новому загальному означенні поняття функції робився на відповідності.
У другій половині XIX ст. після створення теорії множин в означення функції, крім ідеї відповідності, включено ще й ідею множини: «Якщо кожному елементу х множини А поставлено у відповідність деякий певний елемент у множини В, то кажуть, що на множині А задана функція у = f (х), або що множина А відображається на множину В». Таке означення функції можна застосовувати не лише до величин і чисел, але і до інших математичних об'єктів, наприклад до геометричних фігур. Однак математичний аналіз обмежувався дослідженням тільки числових функцій, тобто таких, область визначення і множина значень яких — множини числові. Тобто він продовжував ґрунтуватися на означенні П. Діріхле.
Але вже з початку XX ст. виникла необхідність подальшого розширення поняття функції в іншому напрямі. Особливо гострою вона стала після видання в 1930 р. книги англійського фізика П. Дірака «Основи квантової механіки», в якій розглядалась так звана дельта-функція, яка виходила далеко за межі класичного означення функції.
За означенням П. Дірака, дельта-функція — це функція у = ![]() (х), яка дорівнює нулю для всіх х, -
(х), яка дорівнює нулю для всіх х, -![]() < х < +
< х < +![]() , крім х = 0, а для х = 0 перетворюється у нескінченність.
, крім х = 0, а для х = 0 перетворюється у нескінченність.
У зв'язку з цим у 30-40-х pp. XX ст. радянський математик М. Гюнтер та інші вчені видали праці, в яких розглядали не функції точки, а «функції області», що краще відповідало фізичній сутності досліджуваних явищ. У загальному вигляді поняття узагальненої функції ввів француз Л. Шварц.
У 1936 р. С. Соболєв розглянув частинний випадок узагальненої функції, який включав і дельта-функцію, і застосовував створену теорію до розв’язування низки задач математичної фізики. Важливий внесок у розвиток теорії узагальнених функцій зробили І. Гельфанд, Г. Шилов і інші.
3. Історія розвитку сучасних розділів математики: комбінаторики, теорії ймовірностей, математичної статистики, топології, фрактальної геометрії й фрактального аналізу. Розвиток математики в Україні.
Історія розвитку комбінаторики
Комбінаторика — розділ математики, присвячений розв'язуванню задач вибору і розміщення елементів деякої скінченної множини за допомогою заданих правил. Кожне таке правило визначає спосіб побудови комбінаторної конфігурації — деякої конструкції з елементів заданої множини. Найпростішим прикладом комбінаторних конфігурацій є сполуки: комбінації, розміщення і перестановки.
Комбінаторика вивчає питання існування комбінаторних конфігурацій, алгоритми їх побудови, оптимізації таких алгоритмів, а також розв'язування комбінаторних задач, зокрема визначення кількості конфігурацій даного класу.
Виникнення основних понять і розвиток комбінаторики відбувалися паралельно з розвитком інших розділів математики: арифметики, алгебри, теорії чисел, теорії ймовірностей. Саме#слово «комбінаторика» походить від латинського «combina», що означає сполучати, зв'язувати.
Окремі комбінаторні задачі деякі спеціалісти розв'язували ще до нашої ери. Математики Стародавнього Сходу знали формулу, яка виражала число комбінацій через біноміальні коефіцієнти, а також формулу бінома Ньютона з натуральним показником. Велика увага приділялася вивченню магічних квадратів, які широко використовувалися з магічними цілями. Вивченням комбінацій та перестановок ще в X ст. до н.е. займалися китайські математики. Вони знали і використовували правило знаходження біноміальних коефіцієнтів у розкладі (a+b)n , п є N.
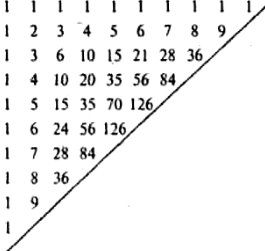
Деякі елементи комбінаторики зустрічалися у працях індійських математиків II ст. до н.е. Інтерес до комбінаторики в Стародавній Індії визначається широким застосуванням там правил ведійського віршоскладання. Для створення віршів різних розмірів (6, 8, 9, 11, 12 складів) необхідно було врахувати не тільки кількість складів, але й довжину голосних звуків у кожній складовій групі. У трактаті «Чхандах-сутра» Пінгали (200 р. до н.е.) описувався метод знаходження числа комбінацій з «складів, які беруться по 1, 2, 3,...., n складів одночасно. Цей метод називався «меру-простара» і описувався у такий спосіб: «Після побудови квадрата на вершині, нижче будуються ще два квадрати так, щоб половина кожного розташовувалась під кожною з двох сторін. Потім побудуємо три квадрати, ще нижче — чотири квадрати; процес повторюється до тих пір, поки потрібна піраміда не буде отримана. В першому квадраті запишемо одиницю; в кожному з двох квадратів другої лінії знову розташуємо по одиниці. У третій лінії одиницю розташуємо в кожному з двох крайніх квадратів. У середньому квадраті цієї лінії треба розмістити суму чисел ближчих двох квадратів, розташованих вище. В четвертій лінії одиницю розташуємо в кожному з двох крайніх квадратів, у кожному з сусідніх квадратів розташуємо суму чисел ближчих двох квадратів, написаних вище, тобто 3. Таким самим способом продовжуємо заповнювати всі квадрати. Тоді друга лінія дає число комбінацій з короткого та довгого звуків, які утворюють один склад; третя дає те саме для двох складів, четверта — для трьох складів і т. д.»
|
|
|
1 |
|
|
|||||||
|
|
|
1 |
1 |
|
|
||||||
|
|
|
1 |
2 |
1 |
|
|
|||||
|
|
|
1 |
3 |
3 |
1 |
|
|
||||
|
|
1 |
4 |
6 |
4 |
1 |
|
|||||
|
1 |
5 |
10 |
10 |
5 |
1 |
||||||
Як бачимо, метод «меру-простару» дає спосіб визначення біноміальних коефіцієнтів, який використовувався для розв'язування комбінаторних задач. Згодом таке розташування чисел назвали трикутником Паскаля, хоча індійські математики знали його майже на 1000 років раніше, ніж Паскаль. Індійські математики в II ст. до н. е. не тільки вміли обчислювати значення С![]() , а й знали співвідношення:
, а й знали співвідношення:
С![]() + С
+ С![]() + С
+ С![]() + … + С
+ … + С![]() = 2n.
= 2n.
Окремі правила і задачі з комбінаторики містилися у віршах Магавіри, Шрідхари, Бхаскари II, Нарайани. Зокрема, у Магавіри словесно подавалося правило знаходження числа комбінацій:
С![]() =
= ![]() .
.
Автор ілюстрував його трьома прикладами. Наведемо один з них: «О друже, скажи скільки різних намистин можна отримати з діамантів, сапфірів, смарагдів, коралів і перлин?»
Невеликий розділ, присвячений сполукам, міститься в «Патіганіті» Шрідхари. Він складається з двох правил і одної задачі. Перше правило — це формула для знаходження числа комбінацій із п елементів, взятих по 1, 2, 3,.., т,..., п елементів, яка подається у вигляді:
![]() .
.
Для ілюстрації цього правила Шрідхара наводить приклад: «Кухар готує різні страви з шести смаковими відтінками: гострий, гіркий, терпкий, кислий, солоний, солодкий. Друже, вкажи число всіх різновидів». Розв'язання подає таке. «Запишемо по черзі числа від 1 до 6, а саме: 6|5|4|3|2|1 — а потім запишемо їх від 1 до 6, а саме: 1|2|3|4|5|6.
Розділимо числа першого ряду на відповідні числа другого ряду, отримаємо:
6|5|4|3|2|1
1|2|3|4|5|6 .
Спочатку маємо ![]() = 6, це число страв з одним смаковим відтінком: гострий, гіркий, терпкий, кислий, солоний, солодкий. Потім маємо
= 6, це число страв з одним смаковим відтінком: гострий, гіркий, терпкий, кислий, солоний, солодкий. Потім маємо ![]() = 15, це число страв з двома смаковими відтінками: гостро-гіркий, гостро-терпкий і т.д. Потім маємо 15
= 15, це число страв з двома смаковими відтінками: гостро-гіркий, гостро-терпкий і т.д. Потім маємо 15![]() = 20, це число страв з трьома смаковими відтінками: гостро- гірко-терпкий, гостро-гірко-кислий і т. д. Потім маємо 20
= 20, це число страв з трьома смаковими відтінками: гостро- гірко-терпкий, гостро-гірко-кислий і т. д. Потім маємо 20![]() = 15, це число страв з чотирма смаковими відтінками: гостро-гірко-терпко-кислий і т. д. Потім 15 •
= 15, це число страв з чотирма смаковими відтінками: гостро-гірко-терпко-кислий і т. д. Потім 15 •![]() = 6, це число страв з п'ятьма смаковими відтінками: гостро-гірко-терпко-кисло-солоний. Потім 6
= 6, це число страв з п'ятьма смаковими відтінками: гостро-гірко-терпко-кисло-солоний. Потім 6![]() = 1, це число страв із шістьома смаковими відтінками: гостро-гірко-терпко-кисло-солоно-солодкий. Отже, маємо 6; 15; 20; 15; 6; 1 комбінацій. їх сума 63». Значення С
= 1, це число страв із шістьома смаковими відтінками: гостро-гірко-терпко-кисло-солоно-солодкий. Отже, маємо 6; 15; 20; 15; 6; 1 комбінацій. їх сума 63». Значення С![]() не розглядали. Йшлося про формулу
не розглядали. Йшлося про формулу
С![]() + С
+ С![]() + … + С
+ … + С![]() = 2n – 1.
= 2n – 1.
В Європі на початок XVII ст. накопичилось чимало знань з комбінаторики, які стосувалися: властивостей фігурних чисел, побудови магічних квадратів, властивостей біноміальних коефіцієнтів (П. Апіа, М. Штіфель, Н. Тарталья, П. Епігон, А. Такке та інші).
Значний внесок у систематизацію елементарних відомостей з комбінаторики зробили Б. Паскаль і П. Ферма. Зокрема, Б. Паскаль у праці «Трактат про арифметичний трикутник» (1665) описав прийом побудови коефіцієнтів розкладу (a+b)n для різних показників степеня. Всі коефіцієнти Паскаль розташував у вигляді трикутника, принцип побудови якого полягав у наступному:
1) у горизонтальному рядку записувались один за одним деяка кількість одиниць;
2) у наступному рядку під кожним з чисел першого записували суму цього числа з усіма, які знаходяться від нього зліва;
3) чисел у кожному наступному рядку на одне менше, ніж у попередньому. Числа, які розташовані на основах рівнобедрених трикутників, дають коефіцієнти різних степенів бінома.
Н арис. підкреслено коефіцієнти для розкладів:
(a + b)2 – (1; 2; 1)
(a + b)5 – (1; 5; 10; 5; 1)
(a + b)9 – (1;9; 36; 84; 126; 84; 36; 9; 1)
Арифметичний трикутник Паскаля, що розглядається, давав можливість записати вираз будь-якого степеня бінома з натуральним показником. Розклад бінома для загального випадку (a+b)т , n є R, запропонував уперше І. Ньютон.
Він показав, як утворюються коефіцієнти розкладу множенням за допомогою формули:
(a + b)n = an + nbn-1 + ![]() +
+ ![]() + … +
+ … + ![]() + … (*)
+ … (*)
Застосовуючи цю формулу для натурального п, у правій частині рівності завжди отримують скінченну кількість членів, а саме: n+1 — коефіцієнти яких співпадають з відповідною n-ою стороною трикутника Паскаля. Основна заслуга I. Ньютона полягала в тому, що він поширив формулу бінома на випадок довільного дійсного n. У випадку дробових і від'ємних показників кількість членів розкладу бінома завжди нескінченна, тобто зводиться до нескінченних рядів.
I. Ньютон вперше став систематично застосовувати відмінні від натуральних показники бінома. Поширення формули (*) на дійсні показники мало велике значення для подальшого розвитку математики. Саме тому формулу (*) і для натурального п називають біномом Ньютона.
Як наукова дисципліна комбінаторика сформувалася лише у другій половині XVII ст. її наукове обґрунтування дав І. Лейбніц у праці «Міркування про комбінаторне мистецтво» (Dissertatio de art combinatorial», 1666 p.), звідки й отримала назву ця галузь математики.
І. Лейбніц багаторазово повертався до ідеї комбінаторного мистецтва. Його він розумів досить широко, зокрема, як складову будь-якого дослідження, будь-якого творчого акту, що передбачає спочатку аналіз (поділ цілого на частини), а потім синтез (об'єднання частин у ціле). Близько 1700 року І. Лейбніц удосконалив комбінаторну символіку за допомогою розвинутої системи індексів.
У 1713 р. Я. Бернуллі опублікував твір «Мистецтво припущень», в якому з достатньою повнотою виклав відомі на той час комбінаторні факти. Твір складався з 4-х частин, друга з них присвячувалася комбінаториці і містила формули:
• для числа перестановок з п елементів;
• для числа комбінацій (без повторень і з повтореннями);
• для числа розміщень.
В цьому творі Я. Бернуллі створив комбінаторику як основний для того часу апарат розв'язування теоретико-ймовірнісних задач. Тут він довів важливий частинний випадок закону великих чисел (теорема Бернуллі). Розглядаючи суми, що мають вигляд ![]()
![]() , він відкрив числа, які пізніше назвали його ім'ям.
, він відкрив числа, які пізніше назвали його ім'ям.
Твір Я. Бернуллі перевищив роботи його попередників математичністю, простотою методівта чіткістю викладання. Автор використовував найпростіші і наочні методи, супроводжуючи їх чисельними таблицями і прикладами. Протягом XVII ст. твір Я. Бернуллі «Мистецтво припущень» користувався популярністю не лише як серйозний науковий трактат, але і як навчально-довідкове видання.
Великий внесок у розвиток комбінаторних методів зробив Л. Ейлер. У його роботах, присвячених розбиттю натуральних чисел на доданки, покладено початок одному з основних методів перерахунку комбінаторних комбінацій.
Майже до кінця XVIII ст. суттєвого удосконалення загальної теорії комбінаторики не відбувалося. Основні зусилля математиків цього часу зосереджувалися на розв'язуванні конкретних комбінаторних задач. У кінці 70-х років XVIII ст. в Німеччині сформувалась багаточисельна комбінаторна школа, засновником і керівником якої був К. Гінденбург. Він започаткував і довгий час видавав «Збірник комбінаторно-аналітичних задач». Вчені, що належали до цієї школи (Г. Ешенбах, X. Крамп, Й. Пфафф, Г. Роте), намагалися побудувати загальну теорію комбінаторики, використовуючи нескінченні ряди. З цією метою вони вивчили велику кількість їх перетворень: множення, ділення, піднесення до степеня тощо. Через 50 років ця школа вичерпала можливості існуючих методів і розпалася.
Новий розвиток комбінаторика отримала в середині XX ст. у зв'язку з бурхливим розвитком кібернетики, дискретної математики, теорії планування, теорії інформації та широким використанням електронно-обчислювальної техніки. В цей період активізувався інтерес і до класичних комбінаторних задач.
Класичні комбінаторні задачі — це задачі переважно розважального змісту на зразок головоломок, які зводяться до вибору і розташування елементів скінченної множини.
Одна з таких задач зустрічалася ще в міфах Стародавнього Сходу — побудова магічного квадрата, тобто розташування перших п2 натуральних чисел у квадраті n х n так, щоб усі суми рядочків, стовпчиків і діагоналей дорівнювали одному й тому самому числу. Наприклад.
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
Комбінаторними задачами цікавився Л. Ейлер. Це, зокрема, задача про кенігсберзькі мости та задача про 36 офіцерів. Остання полягає в тому, щоб вказане число офіцерів 6 різних військових звань із 6 різних полків потрібно так розташувати в комірках квадрата6x6 (каре), щоб кожна колона і кожна шеренга містили одночасно одного і тільки одного офіцера кожного рангу і кожного полку.
У 1847 Т. Кіркман поставив і розв'язав задачу про 15 школярок. Вони повинні були гуляти щоденно п'ятьма групами по три в кожній групі. При цьому необхідно було так скласти розклад для їх прогулянок, щоб кожна школярка протягом семи днів змогла точно один раз попасти в одну групу з кожною з інших.
Все ж до XX ст. комбінаторним задачам не надавали серйозного значення, а сприймали як математичну розвагу. А у XX ст. комбінаторика піддалась потужному процесу алгебраїзації завдяки роботам Дж. Рота, а пізніше Р. Стенлі. Вивчення ними частково впорядкованих множин, властивостей функцій Мебіуса, абстрактних властивостей лінійної залежності, з'ясування їх ролі для розв'язування комбінаторних задач сприяли збагаченню комбінаторних методів дослідження і подальшої інтеграції комбінаторики в сучасну математику, особливо в теорію ймовірностей.
Виникнення та розвиток теорії ймовірностей
Предметом дослідження теорії ймовірностей є випадкові події. Тому цю науку інколи називають «наукою про випадкове».
Теорія ймовірностей — математична наука, яка вивчає закономірності у випадкових явищах незалежно від їх конкретної природи і дає методи кількісної оцінки впливу випадкових факторів на різні явища.
В історії розвитку теорії ймовірностей можна виділити кілька періодів.
Передісторія теорії ймовірностей. У цей період, початок якого губиться в сивій давнині, ставилися і досліджувалися елементарні задачі, які стосувалися імовірнісних понять. Ще в Стародавньому Китаї, Ірані та Римі були відомі факти стійкості частот випадкових подій, пов'язаних з демографічними даними й даними про постачання великих міст. Думка про те, що закони природи проявляються через масу випадкових подій, викладена в поемі Лукреція Кара «Про природу речей» (98—95 р. до н. е.). Уявлення про ймовірності мали й інші античні філософи, зокрема Демокрiт і Платон.
Значну роль у розвитку інтересу до випадкових подій внесли азартні ігри і стрільба. Аналіз задач, пов'язаних з підрахунком шансів в азартних іграх (в яких виграш залежить не від уміння гравця, а від випадку), сприяв створенню підґрунтя для формування нової математичної теорії. Особливо сприятливою у цьому відношенні була гра в кості, оскільки дослідження можливих випадків для кожного з гравців у ній обмежувалося досить простими й наочними математичними моделями. Особливості гри в кості покладено в основу математичних творів відомих італійських математиків XVI ст.: Д. Кардано «Книга про гру в кості» і Г. Галілея «Про випадання очок під час гри у кості» та ін. У цих працях, а також у творах Л. Пачіолі «Зведений виклад арифметики, геометрії, вчення пpo пропорції і пропорціональність» і Н. Тарталья «Загальний трактат про число та міру» вже робиться спроба виділити нове поняття — відношення шансів, розв'язуються задачі, у яких розглядається добуток незалежних подій, висловлюються деякі міркування щодо закону великих чисел.
Виникнення теорії ймовірностей також пов'язано із запитами азартних ігор. Азартні ігри в ту пору були досить поширені головним чином серед знаті, феодалів і дворян. Один із представників французької знаті, азартний гравець кавалер де Мере написав Б. Паскалю лист, в якому просив відповісти на кілька запитань, що виникли в нього у зв'язку з грою в кості, зокрема на таке, що відбувається частіше під час підкидання грального кубика чотири рази — невипадання шістки або її поява?
Розв'язання цієї задачі приводить до наступних результатів:
1) у разі підкидання кубика 4 рази можуть відбутися всього 64 = 1296 різних випадків;
2) шістка жодного разу не з'явиться в 54= 625 випадках і, отже, з'явиться
хоча б раз у 1296 - 625 = 671 випадках. Таким чином, ймовірність того, що шістка з'явиться хоча б один раз ![]() більше ніж ймовірність невипадання шістки жодного разу
більше ніж ймовірність невипадання шістки жодного разу ![]() .
.
Розв'язання досить складних задач, з якими зверталися зацікавлені особи до Б. Паскаля, П. Ферма, X. Гюйгенса, сприяло розробці основних понять і загальних принципів теорії ймовірностей, у тому разі й правил дій над ними. Вважається, що навіть зародження теорії ймовірностей відбувалося у процесі листування Б. Паскаля і П. Ферма. Наведемо окремі частини листа Б. Паскаля до П. Ферма від 28 листопада 1654 р.
«Більшість людей вважають: якщо вони про щось не мають повного знання (а ми ніколи не маємо повного знання), то вони взагалі нічого про це не знають. Я ж упевнений, що такий погляд глибоко помилковий. Часткове знання є теж знання, і неповна впевненість певною мірою дає деяке значення, особливо коли мені відома міра цієї впевненості. Хто-не-будь може запитати: А чи можна виміряти міру впевненості числом?» Звичайно, відповім я: особа, що грає в азартні ігри, обґрунтовує свою впевненість саме цим. Коли гравець кидає гральну кістку, він наперед не знає, яка саме кількість очок випаде. Але дещо він усе ж знає.
Наприклад те, що всі шість чисел — 1, 2, 3, 4, 5, 6 — мають однакову частку успіху. Якщо ми домовимось прийняти можливість виникнення достовірного за одиницю, то можливість випадання шістки, так само як
і кожного з решти п'яти чисел, виразиться дробом ![]() .
.
...Якщо шанси наставання деякої події і того, що вона не настане, точно збігаються (як, наприклад, у разі кидання монети шанси випадання орла і решки), то я кажу, що міра впевненості в наставанні цієї події становить ![]() тобто вона точно дорівнює мірі впевненості в тому, що ця подія не настане.
тобто вона точно дорівнює мірі впевненості в тому, що ця подія не настане.
... Зауважимо відразу, що міру можливості (впевненості) події я назвав ймовірністю. Я багато розмірковував над вибором відповідного слова і нарешті саме його вважаю найвиразнішим. На мою думку, воно повністю відповідає звичайному слововживанню».
У листуванні Б. Паскаля і П. Ферма зустрічалось і таке важливе поняття, як «математичне сподівання», яке потім широко застосовував X. Гюйгенс для розв'язування різноманітних задач. Б. Паскаль, П. Ферма і X. Гюйгенс у своїх працях використовували теореми додавання і множення ймовірностей, поняття залежних та незалежних подій, математичного сподівання тощо. Перший трактат з теорії ймовірностей написав X. Гюйгенс і видав його в 1657 р. під назвою «De ratiociniis in ludo aleae» («Про розрахунки в азартних іграх»).
Наступний період у розвитку теорії ймовірностей починається з праці Я. Бернуллі «Мистецтво припущення», опублікованій посмертно в 1713 р. Книга складалася з чотирьох частин, присвячених таким питанням: аналіз ідей X. Гюйгенса; вчення про перестановки і комбінації; застосування комбінаторики до гри в кості; застосування отриманих результатів до громадянських, моральних і економічних питань (остання частина залишилася незавершеною). Основним результатом усієї книги була «теорема Бернуллі» — одне з важливіших тверджень теорії ймовірностей, яка є окремим випадком закону великих чисел. Завдяки цій теоремі теорія ймовірностей вийшла за межі питань азартних ігор і стала застосовуватися в багатьох галузях життя і діяльності людини. Наприклад, довголітні спостереження показали, що на кожні 1000 народжень припадає 511 хлопчиків і 489 дівчаток. У питаннях демографії важливе значення має ймовірність народження хлопчика, точне значення якої невідоме. На підставі теореми Бернуллі користуються наближеним її значенням — 0,511.
Продовженням результатів Я. Бернуллі стали роботи М. Бернуллі «Досвід застосування мистецтва припущень до правових питань» (1709), А. Муавра «Вчення про випадок» (1718), Т. Байєса «Досвід розв'язання однієї задачі вчення про випадок» (1763), Д. Бернуллі «Досвід нової теорії міри випадку» (1730) та інші.
Значний вклад у розвиток теорії ймовірностей належить французькому математику П. Лапласу. В окремих мемуарах він настільки розвинув теорію ймовірностей, що в 1812 р. об'єднав усе зроблене ним і його попередниками в монументальне дослідження «Аналітична теорія ймовірностей». Ця книга стала провідною в галузі теорії ймовірностей аж до робіт П. Чебишова. В ній наводилося класичне означення ймовірності подій, яке фактично застосовував ще Д. Кардано і вводили явно Я. Бернуллі і А. Муавр як відношення кількості сприятливих випадків до загальної кількості рівноможливих випадків. П. Лаплас подавав також означення математичного і морального сподівання, теореми додавання і множення ймовірностей незалежних подій, кілька теорем про умовні ймовірносні події. Ще він доводив граничні теореми Муавра — Лапласа про збіжність біноміального розподілу до нормального, користуючись при цьому формулою Маклорена — Ейлера.
Граничні теореми він застосовував до розв'язування задач про урни, в процесі чого вперше ввів в теорію ймовірностей диференціальні рівняння в частинних похідних. П. Лаплас висловлював думку, що граничні теореми є математичним апаратом для дослідження статистичної значущості результатів спостережень і пізнання демографічних законів; він сподівався, що дія цих теорем забезпечить торжество «вічних принципів розуму, справедливості і гуманності». П. Лаплас також докладно розглянув азартні ігри, геометричну ймовірність, теорему Бернуллі та її зв'язок з нормальним розподілом ймовірностей, теорію найменших квадратів тощо. Тільки після праць П. Лапласа стало можливим широке застосування науково обгрунтованих методів у теорії ймовірностей. Більш того, багато пізніших результатів, нібито відкритих іншими математиками, можна знайти у працях П. Лапласа.
Помітний внесок у розвиток теорії ймовірностей XIX ст. зробили також К. Гаусс, С. Пуассон, О. Коші. Зокрема, в роботах Гаусса набула стрункого і зручного до застосування вигляду теорія помилок. Тому нормальний розподіл спочатку в астрономів і природодослідників, а пізніше й у математиків стали називати законом Гаусса, хоча вперше нормальний розподіл розглядався ще А. Муавром, задовго до народження К. Гаусса і широко використовувався П. Лапласом.
Основними здобутками цього періоду, що продовжувався до середини XIX ст., були: побудова основ аналітичних методів у теорії ймовірностей, виведення нормального закону розподілу, доведення граничних теорем, існування різних уявлень про ймовірність (геометрична ймовірність, статистична ймовірність) тощо.
Дослідження з теорії ймовірностей французьких математиків досить швидко стали відомими в Росії і отримали тут новий розвиток. Автором першої роботи з теорії ймовірностей російською мовою був А. Павловський — ректор Харківського університету, учитель М. Остроградського. В 1821 р. у Харкові він опублікував науково-популярну брошуру «О вероятности».
Велику роль у розповсюдженні ідей теорії ймовірностей та математичної статистики в Росії та Україні відіграли видатні українські математики В. Буняковський та М. Остроградський.
В. Буняковський першим в Росії приділив велику увагу прикладним питанням теорії ймовірностей, які він висвітлив майже у двадцяти роботах. У фундаментальній праці «Основи математичної теорії ймовірностей» (1846) В. Буняковський дав оригінальний виклад цієї науки і її застосувань до страхування, демографії, ощадних і пенсійних кас, до визначення похибок спостережень тощо. Крім цього, він провів велику роботу з формування відповідної російської термінології, яка залишилася майже незмінною до наших часів.
Праці М. Остроградського з теорії ймовірностей присвячені розв'язуванню важливих практичних задач. Перша праця (1834) присвячена обчисленню ймовірностей помилок судових трибуналів. Найбільша праця «Про одне питання теорії ймовірностей» (1846) сприяла полегшенню перевірки товарів, які поставлялися армії, і поклала початок статистичним методам бракування. В статті «Про страхування»(1847) дається означення математичного сподівання, яке ілюструється прикладами лотерей і розрахунками страхових платежів. Він пояснював: «Вы, например, взяли лотерейный билет, разумеется, недаром: он чего-нибудь стоит, с ним выкупили надежду на выиграш. Но не дорого ли вы заплатили? Не худо бы знать, чего она стоит? В объявленях о лотереях, публикуемых в газетах, всегда пропускается одно весьма важное обстоятельство, без которого нет средства оценить надежду на выиграш. Вы обыкновенно читаете: «Лотерея состоит из стольких-то отличного качества выиграшей, билеты по такой-то цене можно получить в таком-то месте». Никогда не упоминается о числе всех билетов, а без этого числа вы не имеете средства вычислить вероятность выиграша. Таким образом, вы платите за надежды на выиграш, не зная ее цены, и всегда платите слишком дорого».
Коротка стаття, написана в тому ж році, «Игра в кости» (1847) присвячена роз'ясненню того, що всі лотереї та азартні ігри — не вигідні публіці, але приносять значний, досить легкий і гарантований прибуток їх улаштувальникам. М. Остроградський застерігає: «Такой-то, говорите вы, получил первую ставку и вдруг приобрел состояние, — почему такая же ставка не достанется и мне? Вы невольно сравниваете себя с выигравшими и не хотите подумать, что гораздо естественнее поместить себя в число проигравших, потому что их несравненно более».
Усі ці праці написані російською мовою, опубліковані в доступних широкому загалу періодичних виданнях і носять повчальний характер.
Як вважає Б. Гнєденко, захоплення теорією ймовірностей у першій чверті ХІХст. призвело до появи великої кількості праць, пов'язаних із застосуванням цієї теорії до різних проблем природничих наук та суспільного життя. Багато з цих застосувань давалися без обгрунтувань і сприймалися математиками як «математичні скандали». Тому це захоплення скоро змінилося розчаруванням і повним скептицизмом щодо застосувань теорії ймовірностей до наукового пізнання світу. Подальший розвиток теорії ймовірностей потребував уточнення основних її положень. Потрібно було встановити предмет теорії ймовірностей, область її застосувань, вивчити та підсилити її специфічні методи досліджень. Велику роботу в цьому напрямі провів видатний російський математик П. Чебишов (1821-1894).
П. Чебишов зробив помітний внесок до багатьох розділів математики, зокрема й до теорії ймовірностей, де він узагальнив закон великих чисел, довів центральну граничну теорему для суми незалежних випадкових величин та багато інших результатів.
У 25-літньому віці Чебишов написав першу свою працю — «Досвід елементарного аналізу теорії ймовірностей» (1845), яку в 1846 р. захистив як магістерську дисертацію. Всього він опублікував чотири праці з теорії ймовірностей, але вони мали велике значення для подальшого розвитку цієї дисципліни. Зокрема, у праці «Про середні величини» (1867) він надзвичайно просто й елементарно довів закон великих чисел у загальній формі. Його курс теорії ймовірностей, прочитаний у Петербурзькому університеті, відрізнявся чіткістю формулювань та обґрунтованістю тверджень.
З іменем П. Чебишова пов'язується математизація теорії ймовірності. Незважаючи на те що в XIX ст. теорія ймовірностей із зібрання цікавих і різноманітних задач почала перетворюватися на математичну теорію з чітко окресленою проблематикою, вважається, що на цьому етапі вона ще не стала логічно завершеною математичною дисципліною. Навіть Д. Гільберт у доповіді на Міжнародному конгресі математиків у Парижі (1900) відніс теорію ймовірностей до фізичних наук. Заслуга П. Чебишова полягала в тому, що він фактично включив вчення про випадкові події у більш широке вчення про випадкові величини, зробивши останні об'єктом вивчення теорії ймовірностей.
На думку А. Колмогорова, П. Чебишов створив російську математичну школу, яка стала найкращою у світі з багатьох розділів математики, зокрема і з теорії ймовірностей. Серед найвідоміших учнів П. Чебишова слід назвати А. Маркова та О. Ляпунова, які стали видатними математиками саме завдяки своїм дослідженням у теорії ймовірностей.
Закон великих чисел Чебишова поширили на неперервні випадкові величини професор Новоросійського університету 1. Слешинський («К теории способа наименьших квадратов» 1892) і професор Харківського університету М.Тихомандрицький («Курс теории вероятностей» 1898).
Розвиток теорії ймовірностей у кінці XIX на початку XX ст. призвів до необхідності уточнення і перегляду її логічних основ, насамперед — самого поняття ймовірності. Наприкінці XIX ст. французький математик Ж. Бертран (1822-1900) навів ряд парадоксів, пов'язаних з теорією ймовірностей, а А. Пуанкаре узагальнив ці парадокси, які підкреслювали нечіткість та неточність деяких означень понять теорії ймовірностей. Зробити необхідні уточнення стало можливим за допомогою аксіоматичного методу.
Перші роботи в цьому напрямі виконали С. Бернштейн, Р. Мізес, Е. Борель, А. Колмогоров й О. Хінчин.
Спочатку Е. Борель вказав на ідеї, що пов'язують теорію ймовірностей з метричною теорією функцій дійсної змінної. Трохи згодом О. Хінчин, Є. Слуцький, П. Леві, А. Ломницький та ін. широко розвинули ці ідеї, що виявилися дуже плідними для розвитку науки. Зауважимо, зокрема, що саме на цьому шляху вдалося знайти остаточне розв'язання класичних задач, поставлених ще П. Чебишовим. Ідеї метричної теорії функцій, а згодом і функціонального аналізу дозволили значно розширити зміст теорії ймовірностей. До тридцятих років XX ст. відноситься створення основ теорії стохастичних (ймовірнісних, випадкових) процесів, яка тепер стала основним напрямом досліджень у теорії ймовірностей.
Професор Харківського університету С. Бернштейн ще в 1917 р. надрукував працю «Досвід аксіоматичного обґрунтування теорії ймовірностей», а у 1927 р. — книгу «Теорія ймовірностей», в якій виклав власну аксіоматику теорії ймовірностей. Ця книга вважається однією з найкращих серед творів світової літератури з теорії ймовірностей.
Вирішальним етапом розвитку теорії ймовірностей стали праці А. Колмогорова. В 1931 р. він опублікував німецькою мовою фундаментальну статтю « Про аналітичні методи в теорії ймовірностей», а в 1933 в Берліні німецькою і в 1936 в Москві російською вийшла у світ його славнозвісна монографія «Основні поняття теорії ймовірностей». Цією роботою завершився етап побудови теорії ймовірностей як цілісної математичної теорії. Завдяки аксіоматиці теорія ймовірностей стала абстрактно-дедуктивною математичною дисципліною, тісно пов'язаною з іншими математичними дисциплінами. Після публікації цієї монографії А. Колмогорова визнали у всьому світі як одного з найвідоміших математиків XX ст.
Сучасний розвиток теорії ймовірностей характеризується загальним піднесенням її авторитету, а також розширенням кола її практичних застосувань. У США, Франції, Швеції, Італії, Японії, Великобританії, Польщі, Угорщині, Росії, Україні й інших країнах світу є чимало вчених, що збагачують теорію ймовірностей важливими результатами.
Розвиток математичної статистики
Теорія ймовірностей і математична статистика виникли в середині XVII століття в результаті розвитку суспільства і товарно-грошових відносин.
Свою роль у цьому процесі відіграли й азартні ігри, вони послужили простими моделями для виявлення закономірностей у появі випадкових подій. Крім того, розвиток математичної статистики був обумовлений необхідністю обробляти дані, які зібралися до того часу в області керування державою: демографії, охороні здоров’я, торгівлі й інших галузях господарської діяльності.
Можна перелічити досить довгий список імен великих учених, які додали свого внеску у розвиток математичної статистики: П. Ферма (1601–1665) і Б. Паскаль (1623–1662), Я. Бернуллі (1654–1705) і П. Лаплас (1749–1827), К. Гаусс (1777–1855) і С. Пуассон (1781–1840), Т. Байєс (1701–1761) та ін. Ці імена мають бути вже відомі читачам з назв часто застосовуваних статистичних процедур, тестів і розподілів.
Першим, хто вдало об’єднав методи антропології і соціальної статистики з досягненнями в області теорії ймовірностей і математичної статистики, був бельгійський статистик Л. Кетле (1796–1874).
З його робіт випливало, що задача статистики полягає не лише у збиранні і класифікації даних, а й у їхньому аналізі з метою відкриття закономірностей. Л. Кетле одним з перших показав, що випадковості, які спостерігаються в живій природі, внаслідок їхньої повторюваності виявляють певну тенденцію, яку можна описати мовою математики. Л. Кетле заклав і основи біометрії.
Створення ж математичного апарату цієї науки належить англійській школі статистиків XIX століття, на чолі якої стояли Ф. Гальтон і К. Пірсон. Розроблені Ф. Гальтоном (1822–1911) і К. Пірсоном (1857–1936) біометричні методи увійшли в золотий фонд математичної статистики.
Пірсон запровадив у біометрії такі поняття, як середнє квадратичне відхилення і варіацію, йому належить розробка методу моментів, критерію згоди ![]() 2, він увів термін «нормальний розподіл», який зараз загальноприйнятий у багатьох країнах. (Відомо ще багато варіантів назви цього розподілу, наприклад, лапласів розподіл, гауссів розподіл, розподіл Гаусса-Лапласа, розподіл Лапласа-Гаусса.
2, він увів термін «нормальний розподіл», який зараз загальноприйнятий у багатьох країнах. (Відомо ще багато варіантів назви цього розподілу, наприклад, лапласів розподіл, гауссів розподіл, розподіл Гаусса-Лапласа, розподіл Лапласа-Гаусса.
Як апроксимація до біноміального розподілу він розглядався Муавром ще в 1733 р., однак Муавр не вивчав його властивостей.) К. Пірсон удосконалив запропоновані Гальтоном методи кореляції і регресії. Термін «регресія» був введений Ф. Гальтоном у 1886 р. Гальтон встановив, що в середньому сини високих батьків мають не такий великий зріст, а сини батьків з невеликим зростом вище за своїх батьків. Це було інтерпретовано ним як «регресія до посередності». Помилки в міркуваннях Гальтона були роз’яснені пізніше, приміром, Браунлі.
Однак вчені не відразу оцінили переваги, які давало використання математичної статистики в природознавстві. Положення дещо змінилося на краще, коли була обґрунтована теорія малих вибірок.
Піонером у цій області був учень Пірсона В. Госсет, який опублікував у журналі «Біометрика» свою статтю під псевдонімом Стьюдент (звідси – критерій Стьюдента). Вважається, що цінність роботи Стьюдента полягала не у значних числових змінах під час розрахунку тестової статистики. Багато вчених задовго до Стьюдента використовували співвідношення, яке тепер має його ім’я, але без урахування обсягу вибірок (числа ступенів свободи) і співвідносили отриманий результат з таблицями стандартного нормального розподілу (аналог критерію Стьюдента для нескінченного числа ступенів свободи), користуючись при цьому різними застереженнями під час інтерпретації результатів.
Цінність роботи Стьюдента полягає в усвідомленні того, що треба брати до уваги «капризи» малих вибірок, причому не тільки в тій задачі, з якої починав Стьюдент, але й у всіх подібних. Крім того, він розробив таблиці, які можна використовувати для визначення довірчих інтервалів і перевірки критеріїв значимості навіть на основі дуже малих вибірок, що дає можливість вирішення багатьох статистичних задач.
Подальший розвиток теорія малих вибірок одержала у працях Р. Фішера (1890–1962), основне місце в його роботі займали питання планування експерименту. Фішер запропонував цілий ряд нових термінів і понять, розглянув фундаментальні принципи статистичних висновків, показав, що планування експериментів і обробка їхніх результатів – дві нерозривно пов’язані задачі статистики.
Не можна не відзначити той величезний внесок, що зробили в розвиток теорії ймовірностей і математичної статистики російські вчені: О.Я. Хінчін (1894–1959), О.І. Хотимський (1892–1939), Б.С. Ястремський (1877–1962), В.І. Романовський (1879–1954), А.А. Ляпунов (1911–1973), А.Н. Колмогоров та його школа і багато інших.
У сучасній статистичній науці існує розподіл на дві основні школи: найбільш численна класична школа – послідовники Фішера і його учнів, а також суб’єктивістська, чи байєсівська школа.
Хоча на рівні прикладної статистики результати, одержані в рамках цих різних наукових шкіл, досить добре погоджуються, з широкого кола теоретичних і філософських питань ці два напрямки часто розходяться, пропонуючи різні підходи до вирішення задач.
Стисло основну розбіжність у підходах можна було б охарактеризувати в такий спосіб: прихильники класичного підходу єдино можливою вважають частотну інтерпретацію імовірності (тому такий підхід називають ще «frequentist school»), суть їхнього підходу полягає в тому, що вони починають вирішення задачі з вибору моделі і перевіряють, чи може дана модель «пояснити» отримані (чи ще більш «екстремальні») дані. Відмінність байєсівського підходу полягає в тому, що до того, як будуть отримані дані, статистик розглядає ступінь своєї довіри до різних можливих моделей і представляє їх у вигляді ймовірностей (апріорні імовірності). Як тільки дані отримані, теорема Байєса дозволяє розрахувати нову множину ймовірностей, що являють собою переглянуті ступені довіри до можливих моделей на основі отриманих даних (апостеріорні імовірності). Оцінка апріорних ймовірностей є суб’єктивною, тому даний підхід і називається суб’єктивістським.
Нині статистична наука продовжує розвиватися. Так, у 90-і роки XX століття була зроблена величезна методологічна робота, яка має безпосереднє відношення до статистичного аналізу. Цікаві роботи вчених-статистиків стосувалися питань метааналізу, перехресного дизайну, досліджень біоеквівалентності, послідовного дизайну вимірювань, що повторюються, тощо.
Досить важко дати вичерпне визначення статистики як дисципліни. Найбільш вдалим можна вважати таке визначення: «наука, що вивчає методи збирання й інтерпретації числових даних».
Таким чином, головна мета статистики – одержання осмислених висновків з неузгоджених (що підлягають розкиду) даних.
Мовою математики, величина будь-якої ознаки, що варіює, є змінною випадковою величиною, а її конкретні значення прийнято називати варіантами.
Взагалі словом «ефект» незалежно від його медичного змісту ми називатимемо будь-які прояви дії досліджуваного, які обрані дослідником для демонстрації його ефективності, безпеки тощо.
Статистику ще часто називають наукою прийняття розумних рішень в умовах невизначеності. При цьому двом категоріям задач статистики приділяють особливу увагу: статистичне оцінювання і перевірка статистичних гіпотез. Перша задача поділяється на точкове та інтервальне оцінювання параметрів розподілу.
Взагалі статистичні задачі з’являються тоді, коли необхідно дати найкращі, у певному розумінні відповіді за обмеженою кількістю спостережень. Якби кількість спостережень не була обмеженою, можна було б точно визначити параметри розподілів і порівняти їх, при цьому ніякої статистичної задачі не було б. Якщо в ході досліджень ми могли б вивчити всі об’єкти сукупності, які нас цікавлять, то можна було б сказати, що ми маємо справу із суцільним вивченням генеральної сукупності.
Насправді обстежувати всі об’єкти сукупності вдається рідко, зазвичай доводиться вивчати лише вибірку, сподіваючись, що ця вибірка досить добре показує властивості досліджуваної сукупності.
При цьому також виникають важливі статистичні задачі: випадковий відбір варіантів з генеральної сукупності і репрезентативності вибірки, а також визначення необхідного обсягу вибірки для формування статистично значимого висновку за результатами проведених досліджень.
Усі статистичні методи виходять з припущення, що дані вилучені із сукупності випадково. А це означає, що імовірність виявитися обраним для всіх членів сукупності має бути однакова.
Наступна важлива математична задача – визначення необхідного обсягу вибірки. Під «необхідним» розуміють мінімально можливу кількість пацієнтів, включених у дослідження, що при обраному дизайні дозволяє установити наявність статистично значимих розбіжностей між порівнюваними методами.
На жаль, про важливість вирішення цієї задачі згадують, як правило, коли дослідження вже закінчені і починається процес статистичної обробки отриманих результатів. Ця проблема дуже важлива.
При плануванні досліджень дуже важливо сформулювати його мету. Якщо метою проведеного дослідження є встановлення розбіжностей (чи переваг), математично дане питання вирішується зазвичай за допомогою перевірки статистичного критерію (чи тесту). Застосовані для цього процедури пов’язані з формулюванням статистичних гіпотез. Іноді для вирішення цієї задачі застосовують і метод довірчих інтервалів.
Статистична гіпотеза – це твердження, помилкове заперечення якого хотілося б уникнути. Як правило, в області клінічних досліджень прийнято формулювати так звану нульову гіпотезу (Н0) таким чином, щоб це твердження бажано було б відкинути (наприклад, немає розбіжностей в ефекті в порівнювальних методах).
Не можна забувати, що нульовій гіпотезі відповідає альтернативна гіпотеза– це висновок, до якого хотілося б прийти в результаті дослідження (наприклад, ефекти порівнювальних методів різні). З процедурами перевірки гіпотез тісно пов’язані поняття помилки I і II роду.
Так, помилка I роду – можливість помилково відхилити нульову гіпотезу, тобто знайти розходження там, де їх немає. Прийнятна для даного експерименту імовірність помилки I роду називається рівнем значимості а. Помилка II роду виникає тоді, коли ми приймаємо нульову гіпотезу, а вона невірна, іншими словами, не знаходимо існуючу розбіжність. Імовірність знайти наявні розходження, тобто чутливість, чи потужність критерію, дорівнює 1 (за інших рівних умов цей критерій має перевагу, у якого імовірність помилки II роду менше, відповідно чутливість більше).
Крім того, для оцінки справедливості Н0 важливий показник, що зазвичай позначається літерою р і називається р-значенням. Він оцінює імовірність того, що значення критерію виявиться не менше критичного значення за умови справедливості нульової гіпотези (тобто за відсутності розбіжностей між порівнювальними групами).
Говорячи про дизайн дослідження, зазвичай мають на увазі його основні компоненти: встановлення порядку проведення дослідження чи плану, визначення обраних методів і ступеня сліпоти, оцінку необхідної кількості пацієнтів, що включаються.
Найбільш часто зустрічаються такі варіанти планів дослідження: перехресний план, план латинських квадратів, мультиперехресний план, план паралельних груп, блокові плани, план «гра на лідера», послідовний план.
Історія розвитку топології
Топологія — найбільш абстрактна галузь сучасної математики, яка вивчає ідеї неперервності. Предметом топології є дослідження властивостей фігур та їх взаємного розташування, які зберігаються при гомеоморфізмі. Центральне поняття топології — гомеоморфізм — не потребує для свого означення ніяких класичних геометричних понять, таких, як відстань, прямолінійність, гладкість тощо, а тільки передбачає, що точки досліджуваної фігури знаходяться в деякому відношенні близькості.
Ввівши поняття топологічного простору множини довільних елементів, які характеризуються відношенням «нескінченної близькості», топологію можна означити як науку, яка вивчає властивості типологічних просторів, що не змінюються при гомеоморфізмі.
Гомеоморфізм — це таке перетворення, за якого виконуються дві умови:
1) кожна точка однієї фігури переводиться в одну і тільки в одну точку іншої фігури;
2) точка М, яка нескінченно наближується до деякої фіксованої точки К однієї з фігур, переводиться в точку М' іншої фігури, яка також нескінченно наближується до точки К’, відповідної т. К.
Наприклад, гомеоморфним будуть куб, сфера, еліпсоїд. Не гомеоморфним — відрізок і коло, коло і лемніската (вісімка), поверхні кулі і тора.
Ідея вивчення топологічних властивостей фігур вперше зустрічається влисті І. Лейбніца до Х. Гюйгенса від 1679р. В ньому Г.Лейбніц пропонує використовувати геометричний чи лінійний аналіз для вивчення властивостей фігур, пов'язаних не з їх розмірами, а з їх положенням. Від Г. Лейбніца бере початок попередня назва топології — analysis situs (аналіз положення).
Термін «геометрія положення» застосовував Л. Ейлер, розглядаючи задачу про кенігсберзькі мости. Використовував цей термін і топологічно розумів його К. Гаусс. У 1833 р. він так писав щодо цього: «Про геометрію положення (geomctria situs), яку передчував Г. Лейбніц і на яку деякі геометри (Ейлер, Вандермонт) кидали лише слабкий погляд, ми через півтораста років знаємо трохи більше, ніж нічого». К. Гаусс створив кілька нотаток, присвячених питанням топології, але він не публікував їх (як і нотатки з неевклідової геометрії), а лише інколи повідомляв про свої ідеї в листах до друзів.
Суттєву роль у створенні топології відіграли розв'язання Ейлером задачі про сім кенігсберзьких мостів і різні узагальнення теореми про многогранники (В + Г- Р = 2, де В - кількість вершин, Г — кількість граней, Р — кількість ребер опуклого многогранника). Ця теорема справедлива не тільки для опуклих многогранників, але й не для всіх.
Виключення з теореми Ейлера вперше помітив С Люільє, розглядаючи мінералогічну колекцію кристалів, серед яких були непрозорі кубічні кристали сірнистого свинцю, включені в середину прозорих кристалів польового шпату. їх вигляд наштовхнув ученого на думку, що для многогранника з порожниною теорема Ейлера неправильна. Якщо уявити собі куб зі скла, всередині якого розташовано куб із заліза, то для кожного з кубів В + Г - Р = 2. Отже, для куба з кубічною порожниною будемо мати В + Г - Р = 4. С. Люільє помітив також, що теорема Ейлера неправильна і для многогранників на зразок «картинної рами», топологічно еквівалентних тору, — для них В + Г - Р = 0, — і для многогранників з кільцевими гранями («куб, на верхню грань якого припаяно інший куб»), для нього В + Г - Р = 3. У 1813 р. у дослідженні «Мемуари про поліедрометрію» він опублікував свої результати, вказавши, що для многогранників, які мають р наскрізних отворів, має місце загальніше співвідношення: В + Г- Р = 2 - 2р. Люільє гадав, що знайшов усі винятки з теореми Л. Ейлера. Однак у 1832 р. німецький математик Гессель знайшов нові винятки — це «многогранники-близнюки», які спаяні уздовж загального ребра або мають загальну вершину.
Теорема Ейлера про многогранники і його розв'язання задачі про сім кенігсберзьких мостів стали першими паростками нової науки, яка сьогодні відома під назвою топологія.
Термін «топологія» вперше з'явився у праці німецького математика й фізика Й. Лістінга «Попередні дослідження з топології» (1847) Й. Ліс-тінг сам створив цей термін з грецьких слів ![]() — місце і
— місце і ![]() - вчення, і пропонував замінити ним термін І. Лейбніца «geometria situs». Як аргумент з цього приводу він висловлював такі думки:
- вчення, і пропонував замінити ним термін І. Лейбніца «geometria situs». Як аргумент з цього приводу він висловлював такі думки:
• слово «геометрія» нагадує про вимірювання, яке не відіграє жодної ролі в топології;
• термін І. Лейбніца «geometria de position» вже застосовується для позначення проективної геометрії.
У роботі «Попередні дослідження з топології» Й. Лістінг розкрив зміст нової галузі математики: « Під топологією будемо розуміти вчення про модальні відношення просторових образів або про закони зв'язності взаємного положення і слідування точок, ліній, поверхонь, тіл та їх частин чи сукупностей в просторі, незалежно від відношень мір і величин». («Модальними» Й. Лістінг називав властивості фігур, які зберігаються під час неперервних перетворень.)
Основними об'єктами дослідження Й. Лістінга були лінійні комплекси, тобто довільні прямі чи криві лінії або сукупності ліній. У 1862 р. Лістінг публікує роботу «Перетин просторових комплексів, або узагальнення теореми Ейлера про многогранники», в якій подає класифікацію комплексів, доводить низку теорем про просторові комплекси, одна з яких є узагальненням теореми Ейлера про многогранники і перенесенням її на простороні комплекси, гомеоморфні сфери; а також описує односторонню поверхню (лист Мебіуса).
Незалежно під Й. Лістінга і майже одночасно з ним вивченням топологічних властивої гей фігур займався А. Мебіус. Він вперше описав «Лист Мебіуса» (найпростішу односторонню поверхню) та його властивості у праці, поданій ним у І861 р. на конкурс до Паризької академії наук. Новизна ідей та їх поганий мовний виклад не дозволили журі правильно оцінити роботу Мебіуса, і вона не була удостоєна премії.
Зміст цієї роботи га інші результати своїх досліджень він виклав пізніше у статтях «Теорія елементарної спорідненості» (1863) і «Про визначення об'єму поліедра» (1865). У першій статті А. Мебіус розкрив зміст поняття «спорідненість» (як взаємнооднозначне і взаємнонеперервне перетворення), промів класифікацію гомеоморфних між собою поверхонь («уніони», «біноми», «терміони» і т.д.), довів теореми Ейлера і Люільє. У другій і гатті ввів поняття орієнтації многогранника і поверхні. Як приклад і зорієнтованої поверхні навів «лист Мебіуса» і з його допомогою побудувіш приклади «неорієнтованих многогранників», для яких несправодіїииі теореми Ейлера і Люільє і для яких не можливо визначити об'єм.
У 1840 р. А. Мебіус сформулював без доведення ще одну цікаву теорему топології «теорему про чотири фарби». її формулювання дуже просте: на сфері достатньо чотирьох фарб для правильного розфарбовування будь-якої географічної карги (будь-які дві країни зі спільним кордоном не можуть бути іафарбовані в один колір). У 1879 р. А. Кемпе опублікував доведення цієї теореми, яке визнали видатні математиками того часу. Таким чином, теорема Мебіуса вважалась строго доведенною більш десяти років, поки у 1890 році Хівуд не знайшов помилки в доведенні Кемпе.
У 1976 р. американські вчені К. Аннель і В. Хакен отримали перше розв'язання проблеми чотирьох фарб з допомогою обчислювальної машини. Вони проаналізували майже 2000 різних типів карт, і серед них машина не знайшла жодного, карту з якого не можна було б розфарбувати в чотири кольори. Це стало підставою до того, щоб оголосити про остаточне доведення теореми про чотири фарби за допомогою швидкодіючих цифрових обчислювальних машин.
Розвиток топології 50-80-х роках XIX ст. пов'язується з іменем Г. Рімана. Основні ідеї топології Г. Ріман виклав у докторській дисертації «Основи загальної теорії функцій комплексної змінної» (1851). Він користувався терміном Г. Лейбніца «analysis situs» (аналіз положення) і трактував його як частину вчення про величини, що неперервно змінюються, в якому змінні величини вивчаються зовсім незалежно від числових співвідношень, а лише з точки зору просторових співвідношень взаємного розташування і зв'язності.
Завдяки авторитету Г. Рімана термін «analysis situs» протягом більш ніж 50 років використовувався як назва галузі математики, яка зараз називається топологією. Ріман вперше ввів поняття однозв'язних і бага-тозв'язних поверхонь, роду поверхні та ін. Він вивчав перетворення, які допускають розтяг, стиск, згин і кручення. Саме він став засновником топологічної теорії двовимірних поверхонь.
Істотний внесок у розв'язання багатьох задач топології зробив М. Жордан. У роботі «Про деформацію поверхні» (1866) він поширив поставлену Гауссом задачу про знаходження необхідних умов накладання двох гнучких поверхонь одна на іншу без складок і розривів на поверхні, які розтягаються. М. Жордану належить також відома теорема про ге, що замкнута неперервна плоска крива розділяє площину на дві області, внутрішню і зовнішню, причому внутрішня область завжди включає круг скінченного радіуса.
Розділ «Analysis situs» міститься в «Ерлагенській програмі» Ф. Клейна. Автор характеризує його як такий, де «знаходять те, що залишається незмінним підчас перетворень, складених з нескінченно малих деформацій».
У «Замітках про зв'язність поверхонь» (1874) Ф. Клейн доводить, що проективна площина гомеоморфна листу Мебіуса, склеєному з кругом.
У своєму курсі лекцій «Про теорію Г. Рімана алгебраїчних функцій і їх інтегралів» (1882) Клейн помістив спеціальний розділ «Класифікація замкнутих поверхонь за числом р». Він увів поняття нормальної поверхні — еталону, якому гомеоморфні усі поверхні з різними числами р: «Сфера і тор будуть служити нормальними поверхнями для р = 0 і р = 1. Для більших значень р (в якості нормальних поверхонь) можна розглядати сферу з р ручками». В цій роботі означається і так звана пляшка Клейна — одностороння поверхня, про яку, як пише Клейн, «можна скласти собі уявлення, якщо вивернути шматок каучукової трубки і примусити його перетнутися з самим собою у такий спосіб, щоб у разі з'єднання кінців його зовнішня сторона з'єдналася б із внутрішньою».
Відомості про топологію можна знайти також у працях К. Веєрштрасса і Г. Кантора. їх дослідження сприяли виникненню теоретико-множинної топології. Обґрунтування цього напряму в топології зробив Ф. Хаусдорф. Він перший дав загальне означення абстрактно-топологічного простору. Пізніше свої означення запропонували польський математик К. Куратовський і радянський математик П. Александров.
Другий напрям у топології, який називають комбінаторною чи алгебраїчною топологією, поклали початок у 90-х роках минулого століття роботи А. І Іуанкаре.
Об'єднання комбінаторного і теоретико-множинних напрямів топології вперше здійснив Л. Врауср у процесі вивчення поняття розмірності. В 1911 р. він розв'язав одну з перших і найважчих задач я-вимірної топології, довівши неможливість взаємно однозначного і взаємно неперервного відображення один па одного евклідових просторів неоднакового числа вимірювань. Ось чому взаємне відображення куба на квадрат не може бути вза( мно неперервним, оскільки, згідно з теоремою Брауера, куб, який мас три виміри, не гомоморфний квадрату з його двома вимірами. Праці А. І Іуанкаре і Л. Бауера з топології продовжив і розвинув американський вчений Д. Александер. У 1915 році він довів топологічну інваріантність чисел Бетті, а в 1923 р. — так звану основну теорему двоїстості. Теорема двоїстості Александера стала відправним пунктом для одного з найбільших геометричних відкриттів XX ст. — загального закону двоїстості, який сформулював і довів у 1932 р. академік Л. Понтрягін.
Чимало зробили для розвитку топології і радянські математики П. Урисон (побудував загальну теорію розмірності і прочитав в МГУ в 1921/1922 навчальному році перший у СРСР курс топології) і академік П. Александров, який почав свої топологічні дослідження разом з Урисоном і став головою радянської топологічної школи. Застосовуючи методи топології, радянські математики Л. Люстерник і Л. Шнірельман повністю розв'язали в 1929 р. поставлену ще в 1908 р. А.Пуанкаре задачу про три геодезичні лінії. Важливі результати в топології отримали також В. Болтянський, А. Колмогоров, М. Постніков, К. Ситніков та ін.
Історія розвитку теорії фракталів
Все, що створено людиною, обмежено площинами. Коли зустрічається об’єкт у природі, то спочатку можна побачити, що описати його форму можна лише наближено й допоможуть в цьому фрактали. Де закінчуються правильні форми Евклідової геометрії, там зустрічаються фрактали.
Фракта́л (лат. fractus — подрібнений, дробовий) – нерегулярна, самоподібна структура. У широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є подібними до неї самої.
Об'єкти, які тепер називаються фракталами, досліджувались задовго до того, як їм було дано таку назву. В етноматематиці, наприклад в роботах Рона Еглаша "Африканські Фрактали", задокументовано поширені фрактальні геометричні фігури в мистецтві тубільців. У 1525 році німецький митець Альбрехт Дюрер опублікував свою працю “Керівництво Художника”, один із розділів якої має назву "Черепичні шаблони, утворені пентагонами". Пентагон Дюрера багато в чому є схожим на килим Серпінського, але замість квадратів використовуються п'ятикутники. Джексон Поллок (американський експресіоніст 50-тих років) малював об'єкти, дуже схожі на фрактали.
Ідею "рекурсивної самоподібності" було висунуто філософом Лейбніцом, який також розробив багато з деталей цієї ідеї. У 1872 Карл Веєрштрасс знайшов приклад функції з неінтуітивною особливістю, скрізь неперервної, але ніде недиференційованої — графік цієї функції тепер називався б фракталом. У 1904 Хельга Фон Кох, незадоволений занадто абстрактним та аналітичним означенням Веєрштрасса, розробив більш геометричне означення схожої функції, яка тепер має назву сніжинки Коха. Ідею самоподібних кривих, котрі складаються із частин, схожих на ціле, було далі розвинено Полем П'єром Леві, який у своїй роботі "Криві та поверхні на площині та у просторі", виданій 1938 року, описав нову фрактальну криву, відому тепер як Крива Леві (мал. а, б, в).
а) б) в)
Ґеорг Кантор навів приклади підмножин дійсних чисел із незвичними властивостями — ці множини Кантора тепер також визнаються як фрактали.
Ітераційні функції на комплексній площині досліджувались в кінці XIX та на початку XX століття Анрі Пуанкаре, Феліксом Кляйном, П'єром Фату та Ґастоном Жюліа. Проте за браком сучасної комп'ютерної графіки у них забракло засобів відобразити красу багатьох із відкритих ними об'єктів.
У 1975 році Мандельброт використав слово фрактал як назву для об'єктів, розмірність Хаусдорфа яких є більшою за топологічну розмірність, наприклад Крива Хильберта (мал.а,б,в,г).
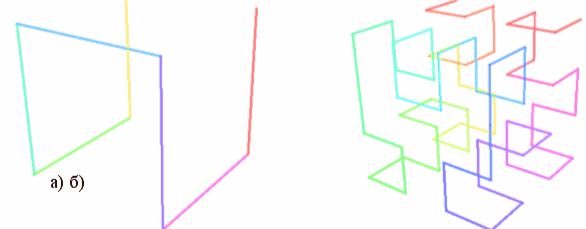

Одним із тих, хто найближче підійшов до результатів, отриманих Б. Мандельбротом, був французький математик Г. Жуліа. У віці 25 років, він видав свій шедевр на 199 сторінках про ітерації раціональних функцій. Ця робота одержала Гран Прі Академії наук, а її автор став відомим у всіх математичних центрах того часу. Дослідження ітерацій функцій комплексної змінної Г. Жуліа проводив разом зі французьким математиком П. Фату. У 1917-1919 pp. вони отримали основні результати, пов'язані з ітерацією функцій комплексної змінної. Цей факт став вражаючим прикладом математичного дослідження, який на багато десятиліть випередив час (вчені могли лише приблизно уявити, як виглядають досліджувані ними об'єкти).
Хоча роботи Г. Жуліа були відомі й активно пропагувалися у 20-х роках XX ст. (у Берліні в 1925 р. було організовано семінари для їх вивчення, участь у яких взяли багато відомих математиків), з часом їх забули, оскільки дослідження подібних фрактальних множин потребували введення загальної теорії міри. Ідея ця висловлювалася ще Г. Кантором і А. Пуанкаре. У 1902 р. запровадив поняття вимірної функції і створив теорію міри А. Лебег, але вона виявилася слабко застосовною для побудови і дослідження фрактальних множин. Розвинув цю ідею німецький математик Ф. Хаусдорф у роботі «Dimension und aueeres Мав (1919), яка вважається першоджерелом з теорії фрактальних множин. Ф. Хаусдорф працював над створенням теорії топологічних і метричних просторів. У 1919 він увів поняття метричної розмірності, яка може бути й дробовою, і навів приклади множин дробової («фрактальної» розмірності). Ідеї Ф. Хаусдорфа, що не опублікував більше жодної роботи в цьому напрямі, були узагальнені і розвинуті далі в публікаціях А. Безиковича. У такий спосіб з'явилося поняття «розмірність Хаусдорфа-Безиковича».
Таким чином, теорія фрактальних множин грунтується на дослідженнях багатьох математиків. У працях Б. Мандельброта використані наукові результати інших учених, які працювали в період 1875-1925 років у тій самій області (Пуанкаре, Фату, Жуліа, Кантор, Хаусдорф, Безикович і ін.). Але тільки в наш час вдалося об'єднати їхні роботи в єдину систему завдяки фундаментальним комп'ютерним експериментам.
У 1982 Б. Мандельброт опублікував роботу «Фрактальна геометрія природи», в якій уперше відмітив фрактальну природу нашого світу:
«Чому геометрію часто називають холодною і сухою? Одна з причин полягає в її нездатності описати форму хмари, гори, дерева або берега моря. Хмари — це не сфери, гори — не конуси, лінії берега — це не кола, і кора не є гладкою, і блискавка не поширюється по прямій. Природа демонструє нам не просто більш високий ступінь, а зовсім інший рівень складності. Число різноманітних масштабів довжин у структурах завжди нескінченно. Існування цих структур кидає нам виклик у вигляді важкої задачі вивчений тих форм, що Евклід відкинув як безформенні, — задачі дослідження морфології аморфного». І математики одержали новий світ геометричних об'єктів. Світ фрактальної геометрії.
Прикладом фрактальних об'єктів є множини Жуліа та Мандельброта.


та множина Мандельброта (а,б,в,г,д).



а)![]() б)
б)![]() в)
в)![]()
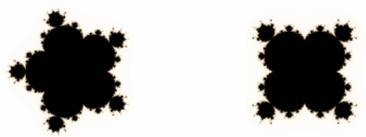
г) ![]() д)
д) ![]()
Про відкриття множини Мандельброта його автор повідомив такі факти. В 1978-1979 роках його зацікавили фрактали інваріантні відносно нелінійних перетворень, Спочатку він з помічником досліджували об'єкт, розглянутий уперше А. Пуанкаре в 1880-х роках — «граничну множину групи Клейна». Згодом їх зацікавила дещо інша задача. На площині задано декілька кіл. Необхідно описати структуру множини, інваріантної за звичайних інверсій щодо будь-якого з цих кіл. Іншими словами, довільно взята початкова точка піддається нескінченному ланцюжку інверсій щодо заданих кіл, і завдання полягає в тому, щоб описати фігуру, до якої нескінченний ланцюжок інверсій «притягає» цю початкову точку. Таку конструкцію вдалося відшукати, а зараз вона здається майже очевидною. Потім вони стали будувати приклади фігур, відомих як «множини Жуліа». Тобто через 35 років відіграли головну роль у відродженні теорії ітерацій.
У 1981 році вийшла книга Д. Хатчинсона «Фрактали і самоподібність», а в 1985 р. М. Барнслі, провідний дослідник фірми Georgia Tech, опублікував свою роботу, в якій увів у математику поняття системи іте-руючих функцій (IFS) та довів, що з їх допомогою можна уявити будь-яке зображення.
Слід зазначити, що незалежно і раніше за Б. Мандельброта «множину Мандельброта» виявили, описали чи спостерігали на дисплеї свого комп'ютера інші математики: Р. Брукс, Дж. Мательські, Дж. Хаббард, Ф. Кочмен, Ф. Рисе. Про це зазначив у «Математичному інформаторі» С. Кранц. Виникла пропозиція вважати їх співавторами відкриття. Щодо цього Б. Мандельброт заперечував у такий спосіб: самі по собі означення або навіть побудови нічого не значать, якщо ви не змогли сказати, чому це важливо, і переконати в цій важливості інших. Тому його претензії на назву множини цілком обґрунтовані.
Після опублікування Б. Мандельбротом результатів своїх досліджень у науці почався дійсний «фрактальний бум». З'ясувалося, що фрактали є чудовим апаратом моделювання і дослідження різноманітних природних явищ. Фрактали широко використовуються у математиці, фізиці, біології, геофізичній гідродинаміці, метеорології, генній інженерії, інформатиці тощо. Крім того, фрактали — галузь мистецтва, коли за допомогою найпростіших формул і алгоритмів утворюються картини надзвичайної краси і складності.
Види фракталів та методи їх створення
Існують три поширені методи створення (генерування) фракталів:
Перший метод — ітераційні функції, які будуються відповідно до фіксованого правила геометричних заміщень, в результаті яких утворюються геометричні фрактали, наприклад: сніжинка Коха.
А також множина Кантора, килим Серпінського, трикутник Серпінського, крива Пєано, крива Коха, крива дракона, Т-Квадрат та губка Менгера є прикладами геометричних фракталів.
Другий метод — рекурентні відношення, це фрактали, що визначаються рекурентним відношенням у кожній точці простору (такому як площина комплексних чисел). Отримані таким методом фрактали називають алгебраїчними.
Прикладами алгебраїчних фракталів є множина Мандельброта, палаючий корабель та фрактал Ляпунова.
Третій метод — випадкові процеси, це фрактали, що генеруються з використанням стохастичних, а не детермінованих процесів, наприклад: фрактальні ландшафти (мал.6 а,б,в,г,д), траєкторія Леві та броунівське дерево.
Типи самоподібності у фракталах
Розрізняють три типи самоподібності у фракталах:
Точна самоподібність — це найсильніший тип самоподібності; фрактал виглядає однаково при різних збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, часто виявляється точна самоподібність.
Майже самоподібність — слабка форма самоподібності; фрактал виглядає приблизно (але не точно) самоподібним при різних збільшеннях. Майже самоподібні фрактали містять малі копії цілого фракталу у перекручених та вироджених формах. Фрактали, згенеровані з використанням рекурентних відношень, зазвичай є майже (але не точно) самоподібними.
Статистична самоподібність — це найслабкіша форма самоподібності; фрактал має чисельні або статистичні міри, що зберігаються при збільшенні. Найприйнятніші означення "фракталів" просто містять в собі деякий вид статистичної самоподібності (розмірність фракталу, саме по собі, є чисельною мірою, що зберігається при збільшенні). Ймовірнісні фрактали є прикладами фракталів, які є статистично, але не майже й не точно самоподібними.
Розмірність фракталів
У евклідової геометрії є поняття розмірності: розмірність крапки — нуль, відрізка та кола — одиниця, круга і сфери — два, кулі — три. З одновимірними об'єктами ми пов'язуємо поняття довжини, з двовимірними - площі і так далі. Але як можна уявити собі множину з розмірністю 3/2? Мабуть, для цього потрібно щось проміжне між довжиною і площею, і якщо довжину умовно назвати 1-мірою, а площа - 2-мірою, то потрібна (3/2) -міра.
У 1919 році Ф. Хаусдорф дійсно визначив таку а-міру і на цій основі кожній множині в евклідовому просторі підставив число, назване їм метричною розмірністю. Він же навів перші приклади множин з дробовою розмірністю. Виявилось, що дробову розмірність мають канторова множина, крива Коха і інші екзотичні об'єкти, до недавнього часу маловідомі за межами математики.
Оскільки фрактал складається з нескінченного числа елементів, що повторюються, неможливо точно виміряти його довжину. Це означає, що чим точнішим інструментом ми будемо його вимірювати, тим більшою виявиться його довжина. Тоді як гладка евклідова лінія заповнює в точності одновимірний простір, фрактальна лінія виходить за межі одновимірного простору, вторгаючись у двовимірне. Таким чином, фрактальна розмірність кривої Коха знаходитиметься між 1 і 2. Найдивовижнішим виявляється те, що й багато природних об'єктів володіють ніби дробовою розмірністю, хоча, відверто кажучи, для природних об'єктів таку розмірність обчислити неможливо. Правильніше сказати, що в певних діапазонах спостереження природні об'єкти, що виникли в результаті довгої дифузії й абсорбції, схожі на фрактальні множини. Наприклад, розмірність узбережжя лежить між 1,01 і 1,6, а кровоносної системи людини — між 3,4 і 3,6
3. Розв’язування історичних задач
1. Дії над алгебраїчними виразами. Тотожності. Розкладання многочленів на множники. Алгебраїчні дроби.
А) Перевірити наступні тотожності, що містяться в геометричній формі в ІІ книзі «Начал» Евкліда:
1. 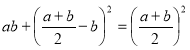 .
.
2. (2a + b)b + a2 = (a + b)2.
3. (a + b)2 + a2 = 2(a + b)a + b2.
4. 4(a + b)a + b2 = [(a + b) + a]2.
5. a2 + b2 = 2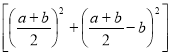 .
.
6. (2a + b)2 + b2 = 2[a2 + (a + b)2].
Б) Перевірити дії з дробами, що були викладені в «Арифметиці» Діофанта:
1. ![]() .
.
2. ![]() +
+ ![]() +
+ ![]() =
=  .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
В) Виконати наступні дії з дробами, які були опубліковані в «Арифметиці» М. Штифеля:
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. ![]() .
.
Г) Скоротити дроби з «Всезагальної арифметики» Ньютона:
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
Д) Перевірити наступні тотожності з «Універсальної арифметики» Ейлера:
1. (р2 - q2) (r2 + b2) = (pr + qs)2 + (ps - qr)2 = (pr – qs)2 + (ps + qr)2.
2. (p2 + q2)2 = ( p2 – q2)2 + (2pq)2 .
3. (p2 + q2)3 = ( p3 – 3pq2)2 + (2p2q – q3)2 .
4. (p2 + q2)4 = ( p4 – 6p2q2 + q4) + (4p3q – 4pq3)2.
2. Лінійні рівняння. Системи лінійних рівнянь
А) З «Московського папіруса».
1. х - ![]() х = 20.
х = 20.
2. (1 + ![]() )х + 4 = 10.
)х + 4 = 10.
3. 2х + х = 9.
Б) З «папіруса Ахмеса»
1. х + ![]() х = 21.
х = 21.
2. (х + ![]() х) -
х) - ![]() ( х +
( х + ![]() х) = 10.
х) = 10.
3. х + ![]() х +
х + ![]() х = 10.
х = 10.
4. х + ![]() х +
х + ![]() х +
х + ![]() х = 37.
х = 37.
5. 3х + ![]() х +
х + ![]() .
. ![]() х +
х + ![]() х = 1.
х = 1.
В) З «Арифметики» Діофанта.
1. ![]() = 3.
= 3.
2. ![]() = 6.
= 6.
3. (b + x) a = ![]() .
.
4. x + y = a, x – 3y = b.
5. x + y = a, ![]() = d.
= d.
6. ![]() = 2,
= 2, ![]() = 3.
= 3.
Г) З алгебри арабського математика і астронома ал-Караджі (X—XI ст.)
1. х + у = 10, ![]() = 1
= 1![]() .
.
2. х + у = 2у, у + 1 = 3х.
3. х + ![]() = 3у, у +
= 3у, у + ![]() = 2х.
= 2х.
Задача Герона Олександрійського.
«Басейн місткістю в 12 кубічних одиниць одержує воду через дві труби, з яких одна дає в кожну годину кубічну одиницю, а інша щогодини - чотири кубичні одиниці. За скільки часу наповниться басейн при спільній дії обох труб?»
Дві задачі Бхаскари.
«З безлічі чистих квіток лотоса були принесені в жертву: Шиві —третю частину цієї множини, Вішну — п'яту і Сонцю — шосту; четверту частину отримав. Бхавані, а решту шість квіток отримав шанований вчитель. Скільки було квіток?»
Хтось сказав другові: «Дай мені 100 рупій, і я буду вдвічі багатшим від тебе». Друг відповів: «Дай ти мені тільки 10, і я стану в 6 разів багатшим за тебе». Скільки було у кожного рупій?
Старовинна задача: «Летіло стадо гусей, назустріч їм летить один гусак і говорить: «Здрастуйте, сто гусей!» Ті йому відповідають: «Ні, нас не сто гусей! Якби нас було ще стільки, скільки є, та ще половина, та четвертина, та ще ти, гусак, з нами, тоді нас би було рівне сто гусей». Скільки їх було?
Задача Бехаеддина.
«Знайти число, яке збільшивши двома третинами самого себе і одиницею дає 10».
З книги «Косс» Адама Pізе (XVI ст.)
«Троє виграли деяку суму грошей. На частку першого припало 1/4 цієї суми, на частку другого 1/7, а на частку третього 17 флорінів.На скільки деким був виграш?»
З книги «Косс» К. Рудольфа (XVI ст.)
«Хтось погодився працювати з умовою отримати в кінці року одяг і 10 флорінів. Але коли минуло 7 місяців припинив роботу і при розрахунку отримав одяг і 2 флоріни. Скільки коштував одяг?»
З «Курсу математики» французького автора Ж. Озанама (ХVІІ ст..)
«Троє хочуть купити будинок за 24 000 ліврів. Вони домовились, що перший дасть половину, другий – третину, а третій – решту. Скільки заплатить кожний?»
З «Всезагальної арифметики» Ньютона.
Дехто хоче розділити між бідними гроші. Якщо у нього було б на 8 динаріїв більше, то він міг би дати кожному по три, та він роздасть тільки по два і у нього лишиться три. Скільки було бідняків?
З «Арифметики» Л. Магницького
«Дехто прийшов на ринок і купив іграшок для малих дітей: за першу іграшку заплатив 1/5 частину своїх грошей, за другу 3/7 остачі від першої покупки, за третю іграшку заплатив 3/5 остачі від другої покупки; а приїхавши додому порахував здачі в гаманці 1 руб. 92 коп., питається, скільки в гаманці було грошей і скільки коштує кожна іграшка?»
З трактату «Математика в дев’яти книгах»
Купляють спільну річ. Якщо кожна людина заплатить по 8, то залишок дорівнюватиме 3. Якщо кожна людина заплатить по 7, то недостача дорівнюватиме 4. Питається: яка кількість людей і яка ціна покупки.
Маємо 5 горобців і 6 ластівок, їх зважили на терезах. Маса всіх горобців більша за масу всіх ластівок. Якщо перемістити 1 ластівку і 1 горобця, то вага буде однаковою. Усі горобці і ластівки разом важать 1 цзинь. Питається, важить ластівка і горобець?»
З «Бахшалійського рукопису»
Знайти число, яке від додавання5 або віднімання 11 перетворюється в повний квадрат.
А) З «Книги абака» Фібоначчі.
1.![]()
![]() .
.
2. ![]() .
.
Б) З книги Регіомонтана (ХV ст..)
1. 10х = х2 +![]() .
.
2. у + ![]() = 25.
= 25.
3. 10х – 60 + ![]() = 80.
= 80.
В) З «Науки про числа в трьох частинах» Миколи Шюке (ХV ст..)
1. 3х2 + 12 = 30х.
2. 144 + х2 = 36х.
Г) Системи рівнянь з «Арифметики» Діофанта.
![]()
![]() 1. х + у = 20, 2. х + у = 20,
1. х + у = 20, 2. х + у = 20,
![]() х2 + у2 = 208. х2 - у2 = 80.
х2 + у2 = 208. х2 - у2 = 80.
![]() 3. х = 3у, 4. х = 3у,
3. х = 3у, 4. х = 3у,
х2 + у2 = 5(х + у). х2 + у2 = 10(х - у).
![]()
![]() 5. х = 3у, 6. х = 3у,
5. х = 3у, 6. х = 3у,
х2 - у2 = 12(х - у). у2 = 6х.
![]()
![]() 7. х = 3у, 8. х – у = 2,
7. х = 3у, 8. х – у = 2,
У2 = 6(х - у). х2 - у2 = (х - у) + 20.
Д) З «Алгебри» аль-Хорезмі.
![]()
![]() 1. х + у = 10, 2. х + у = 10,
1. х + у = 10, 2. х + у = 10,
ху = 21. х2 + у2 = 40.
![]()
![]() 3. х + у = 10, 4. х + у = 10,
3. х + у = 10, 4. х + у = 10,
х2 - у2 = (х - у) + 54. х2 = 4ху.
![]()
![]() 5. х + у = 10, 6. х + у = 10,
5. х + у = 10, 6. х + у = 10,
(х + у)2 = 2![]() х2.
х2. ![]() .
.
![]()
![]() 7. х + у = 10, 8. х + у = 10,
7. х + у = 10, 8. х + у = 10,
у2 = 81х. ху : |у - х| = 5![]() .
.
Е) З «Алгебри» ал-Караджи (ХІ ст..)
![]() 1. х =
1. х = ![]() у,
у,
ху + х + у = 62.
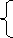 х + у = 10,
х + у = 10,
ху = 4х + 5.
![]()
![]() Є) З «Книги абака» Л. Фібоначчі.
Є) З «Книги абака» Л. Фібоначчі.
1. ху – у = 42, 2. ху + у = 40,
х – у = 2. х – у = 2.
![]()
![]() 3. х + у = 10, 4. х + у = 10,
3. х + у = 10, 4. х + у = 10,
![]() .
. ![]() (х – у) = 24.
(х – у) = 24.
![]()
![]() Ж) З книги «Косс» К. Рудольфа.
Ж) З книги «Косс» К. Рудольфа.
1. (х + у)(х2 + у2) = 539 200, 2. ху + х + у = 573,
(х – у)(х2 – у2) = 78 400. х2 + у2 – х – у = 1716.
Математична мозаїка
Послідовність Фібоначчі.
У XIII столітті італійський математик Фібоначчі розв’язував таку задачу:
Фермер годує кроликів. Кожен кролик народжує одного кролика коли йому стає 2 місяці, а потім дає потомство в 1 кролик кожен місяць. Скільки кроликів буде у фермера через n місяців, якщо спочатку у нього був лише один (вважаємо, що кролики не гинуть і кожен народжений дає потомство за вище описаною схемою)?
Очевидно, що першого та другого місяця у фермера залишається один кролик, оскільки потомства ще немає. На третій місяць буде два кролика, оскільки перший через два місяці народить другого кролика. На четвертий місяць перший кролик дасть ще одного, а другий кролик потомства не дасть, оскільки йому ще тільки один місяць. Отже на четвертий місяць буде три кролики.
Можна помітити, що кількість кроликів після n – го місяця дорівнює кількості кроликів, які були у n – 1 місяці плюс кількість народжених кроликів. Останніх буде стільки, скільки є кроликів що дають потомство, або дорівнює кількості кроликів, яким вже виповнилося 2 місяці (тобто кількості кроликів після n – 2 місяця).
Якщо через Fn позначити кількість кроликів після n - го місяця, то має місце наступне рекурентне співвідношення:
Fn = Fn-1 + Fn-2, F1 = F2 = 1
Покладемо F0 = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... ,
Зображення, яке ілюструє послідовність Фібоначчі.
Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — числова послідовність Fn, задана рекурентним співвідношенням другого порядку
![]()
![]()
і т.д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях - комбінаторних, числових, геометричних.
Суцвіття соняшника з 34 спіралями в один бік і 55 в інший
В природі числа Фібоначчі часто зустрічаються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: ![]() повного оберту в ліщини,
повного оберту в ліщини, ![]() - у дуба,
- у дуба, ![]() - у тополі і груші,
- у тополі і груші, ![]() - у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.
- у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.
Числа Фібоначчі щільно пов'язані з золотим перетином ![]() Формула Біне виражає за допомогою φ значення Fn в явному вигляді як функцію від n:
Формула Біне виражає за допомогою φ значення Fn в явному вигляді як функцію від n:
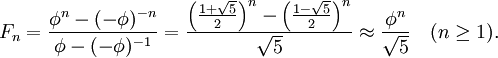
При цьому ![]() і
і ![]() є коренями квадратного рівняння
є коренями квадратного рівняння ![]() .
.
Оскільки − 1 < 1 − φ < 0, знаходимо, що при ![]() Тому з формули Біне випливає, що для всіх натуральних n, Fn є найближчим до
Тому з формули Біне випливає, що для всіх натуральних n, Fn є найближчим до ![]() цілим числом,
цілим числом,  . Зокрема, справедлива асимптотика
. Зокрема, справедлива асимптотика ![]()
Найбільший спільний дільник двох чисел Фібоначчі дорівнює числу Фібоначчі з індексом рівним найбільшому спільному дільнику індексів, тобто: ![]() . В наслідок цього:
. В наслідок цього:
Fm ділиться Fn тоді й тільки тоді, коли m ділиться на n (за виключенням n = 2);
кожне третє число Фібоначчі парне (F3 = 2, F6 = 8, F9 = 34);
кожне четверте ділиться на три (F4 = 3, F8 = 21, F12 = 144);
кожне п'ятнадцяте закінчується нулем (F15 = 610);
два сусідніх числа Фібоначчі взаємно прості;
Fm може бути простим тільки для простих m (за єдиним виключенням m = 4, що пов'язано з F2 = 1). Зворотнє твердження невірно: ![]() хоча 19 — просте число. На даний момент невідомо, чи існує нескінченно багато простих чисел Фібоначчі.
хоча 19 — просте число. На даний момент невідомо, чи існує нескінченно багато простих чисел Фібоначчі.
Використовуючи те саме рекурентне співвідношення, що і на початку, у вигляді Fn = Fn + 2 − Fn + 1, можливо поширити визначення чисел Фібоначчі і на від'ємні індекси:
![]() Неважко переконатися, що F − n = ( − 1)n + 1Fn, тобто одержуємо таку саму послідовність з перемежуючимися знаками.
Неважко переконатися, що F − n = ( − 1)n + 1Fn, тобто одержуємо таку саму послідовність з перемежуючимися знаками.
Знаходження сум.
Суми біноміальних коефіцієнтів на діагоналях трикутника Паскаля є числами Фібоначчі з огляду на формулу
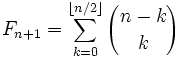 .
.
У 1964 р. J. H. E. Cohn довів, що єдиними точними квадратами серед чисел Фібоначчі є F0 = 0,F1 = F2 = 1 і F12 = 144 = 122.
Множина чисел Фібоначчі співпадає з множиною додатних значення наступного полінома двох змінних
P(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
де ![]() — цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.
— цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.
Сніжинка Коха.
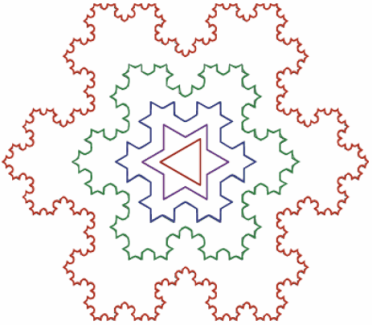
Зобразимо ще один фрактал, який називається сніжинкою Коха. Цей красивий об'єкт теж є результатом нескінченного «дроблення» і добудов.
1-й крок. Побудуємо довільний рів-носторонній трикутник.
2-й крок. Розділимо кожну зі сторін трикутника на 3 рівних частини і замінимо середню частину на дві лінії такої самої довжини, але такі, що лежать зовні трикутника і мають спільну вершину.

3-й крок. Повторимо аналогічні дії з кожною зі сторін утвореної зірки.
Дістанемо фігуру, яку математики називають сніжинкою Коха.

Продовжуючи процес далі, будемо збільшувати кількість сторін многокутника.
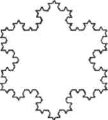
Задача.
Нехай периметр початкового трикутника під час побудови сніжинки Коха дорівнює 9. Чому дорівнюють периметри фігур після кожного кроку? У скільки разів збільшується периметр фігури порівняно з попередньою? Скільки аналогічних кроків (ітерацій) необхідно зробити, щоб отримати периметр не більший, ніж 100? Якщо вважати, що процес зображення сніжинки Коха нескінченний, то чи матиме границю значення периметра? Що станеться з площею сніжинки Коха?
Розв'язання
Периметр початкового трикутника — 9, периметр фігури після 1-го кроку (ітерації) — 12, після 2-го — 16, після 3-го - 21,3(3).
Як бачимо, кожного разу периметр фігури збільшується в ![]() раза порівняно з попередньою фігурою. Це означає, що периметр не має границі.
раза порівняно з попередньою фігурою. Це означає, що периметр не має границі.
Необхідно зробити 8 ітерацій, щоб отримати фігуру, периметр якої приблизно дорівнює 89 (це найближче до 100 число). Після наступної ітерації периметр дорівнює 119.
Площа, на відміну від периметра, має границю. Це легко довести, коли уявити, що початковий трикутник було вписано в коло. На кожному етапі сніжинка Коха залишається в цьому колі, а тому площа сніжинки не більша за площу круга.
Відповісти на запитання, як змінюється площа сніжинки Коха, можна, заповнивши таблицю.
Таблиця
|
№ ітерації |
Площа одного трикутника |
Кількість трикутників |
Площа, яка додасться |
Загальна площа |
|
1 |
9 |
3 |
27 |
108 |
|
2 |
1 |
12 |
12 |
120 |
|
3 |
|
48 |
5,33 |
125,33 |
|
4 |
|
192 |
2,37 |
127,7 |
|
5 |
|
728 |
1,05 |
128,75 |
|
6 |
|
3072 |
0,4682 |
129,21 |
|
7 |
|
12 288 |
0,2081 |
129,43 |
|
|
|
|
|
|
|
8 |
|
49 152 |
0,0924 |
129,522 |
|
|
|
|
|
З наведеної таблиці бачимо, що площа після кожного кроку зростає (для знаходження площі трикутників користуємося формулою S = ![]() ), але зростання стає меншим зі збільшенням номера ітерації.
), але зростання стає меншим зі збільшенням номера ітерації.
Крім того, площа утворює спадну геометричну прогресію зі знаменником ![]() . Отже, площа сніжинки Коха після n-го кроку дорівнює
. Отже, площа сніжинки Коха після n-го кроку дорівнює
81 + ![]() .
.
Це число наближається до 129,6.
Килим Серпинського.
Зобразимо фрактал, що називається трикутником Серпінського.
1-й крок. Зобразимо довільний рівносторонній трикутник. Сполучимо середини його сторін.
Скільки і яких саме трикутників отримали?
Зафарбуємо трикутник, що утворився всередині даного.
2-й крок. Повторимо дії, описані в 1-му кроці, з кожним із трьох незафарбованих трикутників.
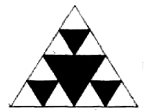
3-й крок. Повторимо дії, описані в 1-му та 2-му кроках, з кожним із незафарбованих трикутників.

У результаті таких дій мають бути зафарбованими 1 великий, 3 середніх і 9 малих трикутників.
Такі дії можна продовжувати нескінченно.

Розглянемо інші фрактали.
Побудуємо губку Серпінського.
1-й крок. Довільний куб розділимо на 27 рівних кубиків і відкинемо центральний кубик і 6 сусідніх.
2-й крок. Кожний із кубиків, що залишився, знову розділимо на 27 кубиків і відкинемо центральний кубик і 6 сусідніх.
Повторюючи аналогічні дії, отримаємо губку Серпінського.

Щоб переконатися, що фрактали є геометричними фігурами, накреслимо криву Пеано.
1-й крок. Побудуємо довільний квадрат ABCD і виділимо ламану, що складається з однієї ланки — сторони АВ квадрата ABCD.
2-й крок. На стороні АВ побудуємо прямокутник ACDB зі стороною АС =
= ![]() АВ і виділимо ламану ACDB, тобто таку ламану, що складається з усіх добудованих відрізків, крім ламаної, виділеної на попередньому кроці.
АВ і виділимо ламану ACDB, тобто таку ламану, що складається з усіх добудованих відрізків, крім ламаної, виділеної на попередньому кроці.
3-й крок. Поділимо відрізок CD точкою Р навпіл і на чотирьох утворених відрізках AC, CP, PD і DB однакової довжини, не виходячи за межі квадрата ABCD, побудуємо прямокутники, другі розміри яких дорівнюють ![]() АС. Виділимо ті відрізки, які є сторонами побудованих прямокутників, але крім тих їх частин, що виділені в попередньому кроці і належать тільки одному з побудованих прямокутників.
АС. Виділимо ті відрізки, які є сторонами побудованих прямокутників, але крім тих їх частин, що виділені в попередньому кроці і належать тільки одному з побудованих прямокутників.
4-й крок і наступні кроки виконуються аналогічно, тобто відрізки, що є більшими сторонами побудованих і залишених сторін прямокутникш ділимо навпіл. На одержаних відрізках як на сторонах, не виходячи за межі прямокутника ABCD, знову будуємо прямокутники. Виділяємо ті відрізки, які є сторонами побудованих прямокутників, але крім тих їх частин, що виділені в попередньому кроці і належать тільки одному з побудованих прямокутників.
У результаті утвориться лінія, що називається кривою Пеано.
Учням можна запропонувати придумати інший, але аналогічний спосіб побудови замкненої кривої без самоперетинів, а потім означити утворену геометричну фігуру.
Зобразимо фрактал, який називається Канторовою досконалою множиною.
1-й крок. Побудуємо довільний відрізок [0; 1], поділимо його на 3 рівні частини і відкинемо середню.
2-й крок. Кожний із двох відрізків, що залишилися, знову поділимо на З рівні частини і відкинемо середні.
Продовжуючи процес поділу і відкидаючи середні частини, отримаємо Канторову досконалу множину. (Точки, що відкидаються, на малюнку чорного кольору.)
![]()
Чи ознайомлені ви з послідовністю чисел, яка носить ім'я французького математика Блеза Паскаля? Числа цієї послідовності вписано в трикутник, який називається трикутником Паскаля.
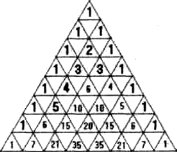
Знайдіть закономірність, за якою вписано числа.
Зафарбуємо парні трикутники в трикутнику Паскаля і отримаємо трикутник Серпінського.

Задача 1.
Розглянемо трикутник Серпінського.
Яка частина трикутника залишилася незафарбованою після 1-го кроку? Яка частина трикутника не буде зафарбованою після 2-го кроку? Яка частина трикутника залишиться незафарбованою після 4-го кроку? Яка частина трикутника не буде зафарбованою після n-го кроку?
Розв'язання
Після 1-го кроку залишиться незафарбованою ![]() трикутника, після 2-го -
трикутника, після 2-го - ![]() , після 3-го -
, після 3-го - ![]() після 4-го —
після 4-го —![]() трикутника.
трикутника.
За неповною індукцією можна припустити, що кожного наступного кроку площа не зафарбованої частини трикутника множиться на ![]() . Тому після n-го кроку не зафарбована площа дорівнюватиме (
. Тому після n-го кроку не зафарбована площа дорівнюватиме (![]() )n.
)n.
Задача 2.
Чи є самоподібним трикутник Серпінського? Скільки є копій початкового трикутника, для яких відношення сторони початкового трикутника до внутрішнього дорівнює 2 : 1; 4 : 1; 8 : 1?
Розв'язання
Зовнішній периметр трикутника Серпінського дорівнює периметру рівностороннього трикутника, всередині якого — нескінченна кількість рівносторонніх трикутників. Усі вони подібні великому зовнішньому трикутнику. Це означає, що трикутник Серпінського є самоподібним.
Існує 3 копії початкового трикутника зі стороною, у 2 рази меншою від сторони початкового трикутника, 9 — зі стороною, в 4 рази меншою від сторони початкового трикутника, 27 — зі стороною, у 8 раз меншою від сторони початкового трикутника, тобто після я-го кроку відношення сторони копії початкового трикутника до сторони самого початкового трикутника дорівнює 2n, а кількість копій — 3n.
Геометрія орнаментів і паркетів.
Паркет (або мозаїка) — нескінченна множина многокутників, що покриває площину без пропусків і перекриттів.
Деякі означення паркету не обмежуються многокутниками. У цьому випадку паркетом називається покриття площини без пропусків і перекриттів заданими фігурами (в окремому випадку — многокутниками, правильними або неправильними, опуклими або неопуклими). У такому випадку навіть для паркету із многокутників може не дотримуватися вимога: два многокутники повинні мати спільну вершину, спільну сторону або зовсім не мати спільної точки. Крім того, з'являється безліч різноманітного паркету, що складається не з многокутників, а з криволінійних фігур.
Паркет з правильних многокутників
Якщо площину розбити на рівні квадрати, то вийде найпростіший паркет. Два квадрати у цьому паркеті мають спільну сторону або спільну вершину, або зовсім не мають спільної точки. Такий же простий паркет складений з правильних трикутників або шестикутників.


Паркетом називатимемо таке покриття площини правильними многокутниками, при якому два многокутники мають спільну сторону або спільну вершину, або зовсім не мають спільної точки.
Красивий паркет можна скласти із правильних шестикутників, квадратів і рівносторонніх трикутників.
 Паркет справляє приємне враження, якщо він симетричний.
Паркет справляє приємне враження, якщо він симетричний.
Паркети із довільних многокутників


Паркети із фігурок тварин

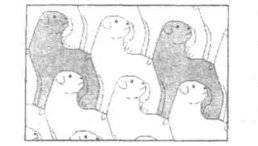

Паркети і сітки з чотирикутників
Якими рівними чотирикутниками можна замостити площину без щілин і накладань, як підлогу паркетинами? Будь-якими.
Нехай маємо довільний чотирикутник ABCD .
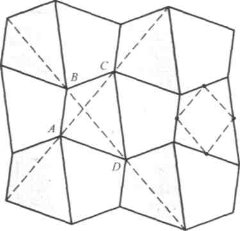
Перенесемо його на вектори п![]() , де n є Z . Одержимо нескінченну послідовність рівних чотирикутників, кожний із яких зі своїм сусіднім має тільки одну спільну точку. Одна діагональ кожного з них лежить на прямій АС, а інші — на паралельних прямих. Якщо утворену таким способом нескінченну послідовність рівних чотирикутників перенести на вектори т
, де n є Z . Одержимо нескінченну послідовність рівних чотирикутників, кожний із яких зі своїм сусіднім має тільки одну спільну точку. Одна діагональ кожного з них лежить на прямій АС, а інші — на паралельних прямих. Якщо утворену таким способом нескінченну послідовність рівних чотирикутників перенести на вектори т ![]() , де т є Z , то вся площина виявиться покритою такими рівними чотирикутниками (на малюнку вони заштриховані). Неважко довести, що і кожний незаштрихований чотирикутник дорівнює заштрихованому, оскільки будь-які два з них, які мають спільну сторону, симетричні відносно середини цієї сторони.
, де т є Z , то вся площина виявиться покритою такими рівними чотирикутниками (на малюнку вони заштриховані). Неважко довести, що і кожний незаштрихований чотирикутник дорівнює заштрихованому, оскільки будь-які два з них, які мають спільну сторону, симетричні відносно середини цієї сторони.
Відзначимо важливі властивості такого замощення площини рівними чотирикутниками. Будь-який заштрихований (незаштрихований) чотирикутник одним паралельним перенесенням можна відобразити на будь-який інший заштрихований (незаштрихований) чотирикутник. А одним поворотом на 180° можна будь-який заштрихований чотирикутник відобразити на незаштрихований і навпаки. 1 під час кожного з таких геометричних перетворень уся нескінченна сітка відображається на себе. Середина кожної сторони кожного чотирикутника цієї сітки — центр симетрії, відносно кожного з яких уся сітка відображається на себе. Усі ці центри симетрії рівномірно покривають всю площину так, що кожні чотири сусідні центри симетрії є вершинами паралелограма.

На малюнку показано, як можна замостити площину рівними опуклими чотирикутниками. Рівними неопуклими чотирикутниками також можна замостити площину.
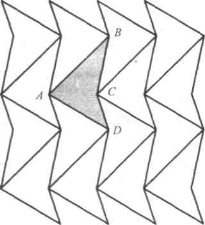
Будь-якими рівними чотирикутниками можна замостити площину.
Замощення періодично повторюються в напрямах АС і BD і в безлічі інших напрямів. Для будь-яких пар цілих значень п і т перенесення сітки з таких рівних чотирикутників на вектор п![]() + т
+ т ![]() відображає цю сітку на себе.
відображає цю сітку на себе.
Замощення площини рівними чотирикутниками (чи іншими плоскими фігурами) мають багато цікавих і важливих властивостей. Тут ми розглянемо тільки одну: звернемо увагу на розташування середніх ліній чотирикутників на такому замощенні. Оскільки середина кожної сторони кожного чотирикутника нескінченної регулярної сітки є центром її симетрії, то дві середні лінії сусідніх чотирикутників симетричні одна одній, тобто лежать на одній прямій (мал.)
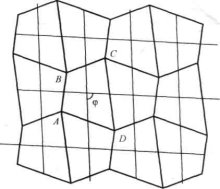
Середні лінії усіх чотирикутників нескінченної регулярної сітки розбивають всю площину на рівні паралелограми. Площа такого паралелограма дорівнює площі чотирикутника ABCD. А нерівні сторони такого паралелограма і кут між ними — це ж середні лінії чотирикутника ABCD і кут між ними. Отже, площа чотирикутника дорівнює добутку його середніх ліній і синуса кута між ними.
Накладання однієї регулярної сітки на другу дозволяє порівняно легко розв'язувати задачі на розрізання. Це питання розглянемо далі, а тут звернемо ще увагу на покриття площини нерівними фігурами, зокрема квадратами.
Розглянемо два квадрати ABCD і AB1C1D1, які мають тільки одну спільну точку А. Точки О і О1 — їх центри.
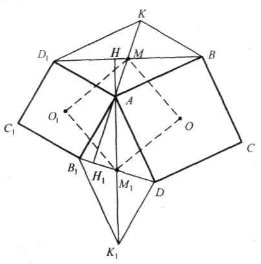
Позначимо точки К і К1, такі, що чотирикутники ABKD1 і AB1K1D — паралелограми. Ці паралелограми рівні, оскільки їхні сторони дорівнюють сторонам квадратів ABCD і AB1C1D1, а кути B1AD і АВК рівні, бо кожен з них у сумі з кутом BAD1 дає 180°. Отже, якщо паралелограм ABKD1 повернути навколо точки 0 на 90°, то він суміститься з паралелограмом AB1K1D . При цьому діагоналі А К і ВD1 займуть положення DB1 і АК1 відповідно. Із сказаного випливають такі властивості розглядуваної конфігурації:
1) трикутники ABD1 і AB1D рівновеликі;
2) медіана AM трикутника ABD1 і висота АН1 трикутника AB1D лежать на одній прямій, як і медіана АМ1 трикутника AB1D і висота АН трикутника ABD1;
3) 2АМ = B1D , 2АМ1 = BD1;
4) оскільки ОМ = ОM1, ОМ ![]() ОM1, і О1М = О1M1, О1М
ОM1, і О1М = О1M1, О1М ![]() О1M1, то чотирикутник MOM1O1 — квадрат;
О1M1, то чотирикутник MOM1O1 — квадрат;
5) точки Н, М, О, M1 , H1 і О1 лежать на одному колі (MM1, — діаметр кола, що проходить через М,О, M1, і О1, а з точок H і H1 цей діаметр видно під прямими кутами);
6) чотирикутник КСК1С1 — квадрат (як гомотетичний квадрату MOM1O1, відносно точки А), КС = 2MO;
7) відрізки BB1 і DD1 рівні та перпендикулярні (вони рівні та паралельні відрізкам СК1 і С1K1).
Майже всі перераховані властивості залишаються правильними, коли один із розглядуваних квадратів прилягає чи накладається на інший.
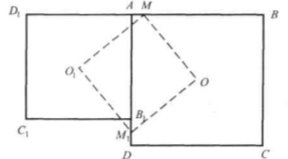
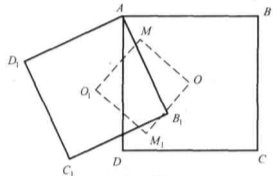
Три визначні задачі давнини.
- Подвоєння куба
Про виникнення задачі подвоєння куба збереглася така легенда: «... під час епідемії чуми послали афіняни в Дельфи запитати оракула, що їм зробити, щоб чума припинилася. Бог відповів їм: подвоїти вівтар і принести на ньому жертви. А оскільки вівтар був кубічної форми, вони понакладали на нього ще один такий же куб, намагаючись таким чином виконати веління оракула. Коли ж чума після цього не припинилася, відправилися вони до Платона і запитали, що ж тепер робити. Той відповідав: «Сердиться на вас бог за незнання геометрії», — і пояснив, що слід було мати на увазі тут не просте подвоєння, але знайти якесь середнє пропорційне і провести подвоєння з його допомогою; і як тільки вони це зробили, чума негайно ж скінчилася». Ця легенда порівняно пізня; в ній багато що спотворено: задачею подвоєння куба займався ще Гіппократ Хіоський, що жив до Платона. Але ця легенда збереглась в кількох джерелах. В ній багато цікавого: для стародавніх греків зовсім не чужою була думка, що боги можуть гніватися за незнання геометрії.
Для практики точне розв’язання задачі подвоєння куба було не потрібне, але математиків вона зацікавила. Гіппократ Хіоський переформулював задачу приблизно так: «За даними відрізками а і 2а побудувати такі відрізки х і у, що а : х = х : у = у : 2а». Насправді, тоді:
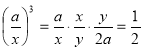
Тобто х3 = 2а2. Це переформулювання було суттєвим. Алгебра виникла набагато пізніше, і старогрецькі математики добуток двох відрізків подавали як прямокутник; для додавання двох добутків відрізків доводилося перетворювати прямокутники в рівновеликі їм прямокутники із спільною стороною, щоб їх можна було прикладати один до одного: добуток трьох відрізків доводилося розглядати вже як паралелепіпед. Перетворювати паралелепіпеди б було дуже складно, а зауваження Гіппократа дозволяло працювати з відношеннями відрізків. Надалі всі розв’язували задачу саме у формулюванні Гіппократа, причому, як правило, в загальному вигляді: відрізок 2а замінювали на довільний відрізок b і будували такі відрізки х і у, що а : х = х : у =у : b '. В цьому випадку

тобто х = ![]() і у =
і у = ![]() . Розв’язання цієї задачі дозволяло також для прямокутного паралелепіпеда будувати ребро куба, об'єм якого дорівнює об'єму паралелепіпеда (із цього слідує, що в одному старогрецькому тексті мовиться: «Після цього ми зможемо взагалі будь-який заданий обмежений паралелограмами об'єм перетворювати на куб...»; цей текст Евдема Родоського, друга і учня Арістотеля, дає пряму вказівку на інтерес математиків до задачі перетворення паралелепіпеда в куб). Пояснимо, як за ребрами прямокутного паралелепіпеда р, q і r можна побудувати ребро потрібного куба. За даними сторонами р і q прямокутника будувати сторону а квадрата, площа якого дорівнює площі прямокутника, уміли вже на найранішому етапі розвитку старогрецької математики. Зрозуміло також, що якщо а =
. Розв’язання цієї задачі дозволяло також для прямокутного паралелепіпеда будувати ребро куба, об'єм якого дорівнює об'єму паралелепіпеда (із цього слідує, що в одному старогрецькому тексті мовиться: «Після цього ми зможемо взагалі будь-який заданий обмежений паралелограмами об'єм перетворювати на куб...»; цей текст Евдема Родоського, друга і учня Арістотеля, дає пряму вказівку на інтерес математиків до задачі перетворення паралелепіпеда в куб). Пояснимо, як за ребрами прямокутного паралелепіпеда р, q і r можна побудувати ребро потрібного куба. За даними сторонами р і q прямокутника будувати сторону а квадрата, площа якого дорівнює площі прямокутника, уміли вже на найранішому етапі розвитку старогрецької математики. Зрозуміло також, що якщо а = ![]() і b = r, то
і b = r, то ![]() =
= ![]() .
.
З різних причин давньогрецькі математики при побудовах циркулю і лінійці віддавали перевагу над всіма іншими інструментами. Тут, потрібно зробити уточнення. Ні про циркуль, ні про лінійку в творах давніх математиків мови немає; мовиться лише про «побудови за допомогою прямих і кіл». Більше того, для Евкліда побудова кола означає не зовсім те ж саме, що використання циркуля. Згідно з третім постулатом Евкліда, можна будувати лише коло з заданим центром А, що проходить через задану точку В. Коло з центром А і радіусом ВС цей постулат будувати не дозволяв (така побудова описана Евклідом в пропозиції 2 книги 1). Циркуль, звичайно ж, дозволив би виконати такі побудови. Напевне, формулювання постулату Евкліда пов'язано з побудовою кола за допомогою кілочка і прив'язаної до нього мотузки. В цьому випадку для побудови кола з центром А і радіусом ВС довелося б спочатку забити кілочок в точці В, помітити на мотузці точку С, а потім висмикнути кілочок і забити його в точці А. Тільки після цього можна було будувати необхідне коло. Така побудова, при якій потрібно було забивати кілочок не один, а двічі, істотно відрізняється від елементарної побудови.
В Греції циркуль був винайдений в X ст. до н. е., задовго до Евкліда, у зв'язку з потребами керамічного виробництва. В цей час широке розповсюдження отримав геометричний стиль, і циркуль був потрібен для зображення на кераміці концентричних кіл.
Грецька міфологія пов'язує винахід циркуля з ім'ям Талоса (згідно іншим джерелам — Пердикса), племінника Дедала. Про Талоса пише давньогрецький історик Діодор Сицілійський (I ст. до н. е.): «Так само, винайшовши циркуль і деякі інші технічні засоби, він досяг великої слави». Римський письменник Гігін (I ст. до н. е.) повідомляє: «Пердикс, син сестри Дедала, винайшов циркуль і пилку з риб'ячого хвоста». Про цей винахід дванадцятирічного хлопчика згадує навіть знаменитий римський поет Овідій (I ст. до н. е.) в поемі «Метаморфози»:
Перший залізним вузлом два залізні кінці сполучив він.
Щоб, коли один від одного вони на відстані рівній.
Частина стояла одна, інша ж круг обводила.
Дедал відомий в грецькій міфології як наймайстерніший винахідник і архітектор. (Дивним чином набагато більш знаменитий нині його безрозсудний син Ікар, який прославився тим, що, не дивлячись на конкретні повчання батька, так і не навчився правильно користуватися зробленими Дедалом крилами з пір’я, що скріпляють воском.) Обдарованість відданого йому в навчання племінника, котра загрожувала затьмарити його славу, викликала у Дедала заздрість, і він зіштовхнув його з акрополя.
* * *
Швидше за все, старогрецькі математики досить швидко зрозуміли, що задачу подвоєння куба не можна вирішити за допомогою циркуля і лінійки, хоча довести цього вони не могли і, мабуть, навіть не намагалися. З приводу того, чим крім циркуля і лінійки можна користуватися при побудовах, у давньогрецьких математиків були різні думки. Перше розв’язання задачі подвоєння куба, отримане великим полководцем і математиком Архитом Тарентським, важко навіть назвати побудовою. Він отримав розв’язання як перетин циліндра, конуса і тора. Ні про яку практичну реалізацію такого розв’язання не могло бути і мови. Дещо більш пізнє рішення Менехма було вже в деякому розумінні оптимальним: він знаходив розв’язок, як перетин двох конічних перетинів. Оптимальним це рішення було ось в якому значенні. На останньому етапі розвитку давньогрецької математики, через декілька століть після Менехма, сформувалася наступна класифікація задач на побудову, викладена олександрійським математиком Паппом:
1) задачі на площині (розв’язувані за допомогою прямих і кіл, тобто за допомогою циркуля і лінійки);
2) просторові задачі (розв’язувались за допомогою конічних перетинів, тобто параболи, гіперболи і еліпса; назва, напевне, пов'язано з тим, що використовувалися перетини просторової фігури — конуса);
3) задачі, розв’язувані тільки за допомогою інших, складніших кривих ліній).
Папп писав, що якщо задачу можна розв’язати за допомогою прямих і кіл, то було б помилкою використовувати в геометрії для її розв’язання інші інструменти. Він був упевнений, що задачу подвоєння куба не можна розв’язати за допомогою прямих і кіл.
Класифікація Паппа неповна. Вона не включає побудови, які використовують спеціальні інструменти, а такі побудови зустрічалися у давньогрецьких математиків нерідко. Спеціальні інструменти для розв’язання задачі подвоєння куба використовували Ератосфен і Нікомед; спеціальний пристрій використаний також в розв’язанні, яке приписували Платону.
* * *
Після давньогрецьких математиків щодо задачі подвоєння куба були отримані, мабуть, лише два істотні результати. По-перше, було обгрунтовано, що ця задача і задача трисекції кута зводяться до розв’язання кубічних рівнянь, а по-друге, в 1837 р. було доведено, що ці задачі нерозв'язні за допомогою циркуля і лінійки (в нерозв'язності цих задач старогрецькі математики, були упевнені, хоча і не могли цього довести). В тому, щоб зрозуміти, що задача подвоєння куба зводиться до розв’язання кубічного рівняння, немає, здавалося б, нічого складного. Але давньогрецькі математики ніколи не вирішували геометричні задачі шляхом зведення їх до рівнянь алгебри. Їх математика була істотно геометричною. Алгебраїзація математики розпочалася набагато пізніше і йшла дуже повільно і важко. Слово «алгебра» зовсім не випадково походить з арабської мови — араби дійсно дуже багато зробили для алгебраїзації математики.
В XII ст. в Європі почали перекладати з арабської мови на латинську трактати старогрецьких і арабських математиків (багато праць давньогрецьких математиків збереглися лише в арабських перекладах). Грецька математика повернулася до Європи в сильно алгебраїзованому вигляді. Великі досягнення в області алгебри (розв’язання в радикалах рівнянь третього і четвертого степеня, теорема Вієта) були вже частково підготовлені.
В своїй книзі «Геометрія» (1637 р.) Декарт показав, як геометричні задачі можна зводити до рівнянь алгебри. У зв'язку з цим у нього виникла задача побудови коренів многочлена. Декарт знайшов дуже простий спосіб будувати корені многочленів третього і четвертого степенів як проекції на вісь координат точок перетину параболи і кола. Як особливо важливі окремі випадки цієї побудови, Декарт виділив розв’язання задач подвоєння куба і трисекції кута і розглянув їх окремо.
Деякий час після появи книги Декарта побудовою коренів займалися майже всі відомі математики (Ферма, Ньютон, ван Схоотен, Лопіталь, Лагір, Я. Бернуллі, Ролль, Крамер, Ейлер), але інтерес до цієї задачі згасав так швидко, що головна теорема, пов'язана з побудовою коренів, залишилася не доведеною, мабуть, і до цього дня. Ця теорема полягає, грубо кажучи, в наступному: корені многочлена n-го степеня можна побудувати як проекції на вісь координат точок перетину двох алгебраїчних кривих, степені яких рівні приблизно ![]() . Останніми з математиків задачею побудови коренів займалися Крамер (1704 — 1752) і Ейлер (1707—1783), але їх інтерес до неї був вже таким слабким, що вони не звернули уваги на майже очевидні речі. Вказану вище теорему хоча і ніхто не доводив, але все таки перевіряли, щоб у кривих було більше вільних коефіцієнтів, які можна змінювати, ніж у многочлена (Лопіталь вважав це цілком достатнім доказом). Щоб уникнути ситуації, коли для многочлена точки перетину кривих виходять уявними, Крамер і Ейлер запропонували спосіб, в якому вільних коефіцієнтів у кривих було менше ніж у многочлена, тобто цей спосіб підходив не для будь-якого многочлена. Напевне, Ейлер не допустив би таку помилку, якби займався цією проблемою всерйоз.
. Останніми з математиків задачею побудови коренів займалися Крамер (1704 — 1752) і Ейлер (1707—1783), але їх інтерес до неї був вже таким слабким, що вони не звернули уваги на майже очевидні речі. Вказану вище теорему хоча і ніхто не доводив, але все таки перевіряли, щоб у кривих було більше вільних коефіцієнтів, які можна змінювати, ніж у многочлена (Лопіталь вважав це цілком достатнім доказом). Щоб уникнути ситуації, коли для многочлена точки перетину кривих виходять уявними, Крамер і Ейлер запропонували спосіб, в якому вільних коефіцієнтів у кривих було менше ніж у многочлена, тобто цей спосіб підходив не для будь-якого многочлена. Напевне, Ейлер не допустив би таку помилку, якби займався цією проблемою всерйоз.
2. Трисекція кута
Про виникнення задачі трисекції кута (тобто розподілу кута на три рівні частини) ніяких цікавих легенд немає. Мабуть, вона з'явилася усередині самої математики у зв'язку з розв’язанням задач на побудову правильних многокутників. Побудова правильного п'ятикутника циркулем і лінійкою повинна була справити на піфагорійців велике враження, тому що правильна п'ятикутна зірка була їх пізнавальним знаком (вона символізувала здоров'я). Відома така легенда. Один піфагорієць помирав на чужині і не міг заплатити людині, яка за ним доглядала. Перед смертю він велів йому зобразити на своєму будинку п'ятикутну зірку: якщо коли-небудь мимо проходитиме піфагорієць, він обов'язково зверне на неї увагу. І дійсно, через пару років опісля якийсь піфагорієць побачив цей знак і нагородив господаря будинку.
За допомогою циркуля і лінійки для n = 6 і 8 правильні n-кутники побудувати можна, а для n = 7 і 9 не можна. Побудова правильного семикутника — цікава задача, її можна розв’язати за допомогою способу «вставок». Побудову правильного семикутника запропонував Архімед. А ось побудова правильного дев'ятикутника, саме котра і повинна була привести до розв’язання задачі трисекції кута, тому що для побудови правильного дев’ятикутника потрібно побудувати кут 360о/9 = 120о/3, тобто розділити кут 120о на три рівні частини.
3. Квадратура круга
Задача квадратури круга, тобто побудови квадрата, рівновеликого даному кругу, в Стародавній Греції була, напевне, дуже популярною. Плутарх повідомляє, що філософ Анаксагор (біля 500 — 428 рр. до н. е.) у в'язниці займався цією задачею. Про неї мовиться і в комедії Арістофана «Птаха» (414 р. до н. е.): «Приклавши сюди лінійку, круг описую циркулем, і вверх і вниз ... Потім лінійкою відношу пряму. Круг тепер подібний чотирикутнику.» Ця згадка в комедії означає, що задача квадратури круга була загальновідома.
Дивним чином задача квадратури круга і зворотна їй задача «кругатури квадрата», тобто побудови круга, рівновеликого даному квадрату, була відома також і в Стародавній Індії. Індійські вівтарі були самої різної форми: у вигляді квадрата, круга, півкола, рівностороннього трикутника, рівнобедреної трапеції, сокола, черепахи і т.д. Але всі ці вівтарі повинні були мати одну і ту ж площу. У зв'язку з цим виникали задачі перетворення круга в рівновеликий йому квадрат і квадрата в рівновеликий йому круг. Розв’язання цих задач зібрані в староіндійській книзі «Сульвасутра», присвяченій побудові вівтарів. Різні частини цієї книги датуються VII — II ст. до н.е. Розв’язання задач, що нас цікавлять містяться в найстародавнішій частині «Сульвасутри».
Побудова круга, рівновеликого квадратові, в «Сульвасутрі» описується так. Опишемо навкруг квадрата АBCD коло. Нехай перпендикуляр до відрізка АВ, проходить через центр О квадрата і перетинає пряму АВ і коло в точках Р і Q відповідно; точка К ділить відрізок PQ у відношенні РК : KQ = 1 : 2. Тоді ОК—радіус круга, площа якого дорівнює площі квадрата. Це розв’язання, звичайно ж, наближене. Якщо а — сторона квадрата, r— радіус побудованого круга, то r = ![]() . Тому із співвідношення а2 = Пr 2 для числа П отримуємо наближене значення
. Тому із співвідношення а2 = Пr 2 для числа П отримуємо наближене значення 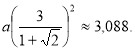
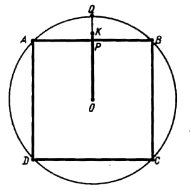
Для розв’язання оберненої задачі, тобто для перетворення круга в рівновеликий йому квадрат, в Стародавній Індії не змогли знайти такої ж простої геометричної побудови і розв’язували її алгебраїчним способом. Це розв’язання слідуюче: якщо d - діаметр круга, а—сторона рівновеликого йому квадрата, то
![]() .
.
Для числа П це обчислення дає наближене значення 3,088.
Ці дуже близькі один до одного наближені значення числа П показують, мабуть, що перше (геометричне) розв’язання в Стародавній Індії вважалося точним. Друге (алгебраїчне) розв’язання явно перетворенням саме цієї геометричної побудови, при цьому використовувалось наближене значення, що зустрічається в книзі «Сульвасутра »
![]()
яке відрізняється від точного значення тільки шостим знаком після коми.
Справді, підставивши у формулу ![]() значення
значення ![]() , отримаємо
, отримаємо ![]() , тобто
, тобто ![]() .
.
Легко перевірити, що
![]() .
.
Відкинувши останній доданок, отримаємо формулу, що міститься в книзі «Сульвасутра». Цей розклад отримуємо майже природним чином:
![]() ;
; ![]() =
= ![]() -
- ![]() .
. ![]() ;
; ![]() =
= ![]() -
- ![]() =
=![]() - -
- -![]() .
. ![]() ;
; ![]() =
= ![]() - (
- (![]() -
- ![]() )=
)=![]() -
- ![]() .
. ![]() ;
; ![]() =
= ![]() - (
- (![]() -
- ![]() )=
)=![]() -
- ![]() .
. ![]()
Єдиний штучний крок в цьому розкладанні полягає в тому, що ![]() <
<![]() <
<![]() , а в якості наближення числа
, а в якості наближення числа ![]() розглядають
розглядають ![]() .
.
В Стародавній Греції задача квадратури круга виникла після того, як була розв’язана задача перетворення многокутника в рівновеликий йому прямокутник. Ця задача розв'язувалася таким чином. Спочатку многокутник розрізали на трикутники. Потім трикутник із стороною а і заввишки ha замінювали на рівновеликий йому прямокутник із сторонами ![]() і ha. Після цього вибирали деякий відрізок е і замінювали кожний прямокутник на рівновеликий йому прямокутник, одна сторона якого рівна е. Як це робилося, показано на мал.; заштриховані прямокутники рівновеликі, тому що вони отримані з двох рівних трикутників шляхом відрізування від них двох пар рівних трикутників. Потім отримані прямокутники із стороною е прикладали один до одного цією стороною і так складали деякий прямокутник. Залишалося побудувати для прямокутника рівновеликий йому квадрат. Ця задача цікава тим, що в книзі «Сульвасутра» і в «Началах» Евкліда описані дуже схожі розв’язання цієї задачі, причому розв’язання далеко не найпростіші.
і ha. Після цього вибирали деякий відрізок е і замінювали кожний прямокутник на рівновеликий йому прямокутник, одна сторона якого рівна е. Як це робилося, показано на мал.; заштриховані прямокутники рівновеликі, тому що вони отримані з двох рівних трикутників шляхом відрізування від них двох пар рівних трикутників. Потім отримані прямокутники із стороною е прикладали один до одного цією стороною і так складали деякий прямокутник. Залишалося побудувати для прямокутника рівновеликий йому квадрат. Ця задача цікава тим, що в книзі «Сульвасутра» і в «Началах» Евкліда описані дуже схожі розв’язання цієї задачі, причому розв’язання далеко не найпростіші.
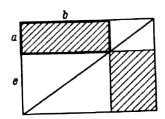
В книзі «Сульвасутра» квадрат, рівновеликий даному прямокутнику АBCD, будувався таким чином. Нехай для визначеності АВ < ВС. Відріжемо від прямокутника АBCD квадрат з стороною АВ і розріжемо прямокутник, що залишився, на два рівні прямокутники; один з цих прямокутників прикладемо до квадрата. В результаті отримаємо фігуру, що заштрихована на мал. Ця фігура є квадратом зі стороною а, з якого вирізаний квадрат із стороною b. Площа цієї фігури дорівнює площі квадрата із стороною х. де х2=а2—b2. Для побудови відрізка х можна скористатися теоремою Піфагора: цей відрізок є катетом прямокутного трикутника з гіпотенузою а і катетом b. В книзі «Сульвасутра» теорема Піфагора описана в слідуючому формулюванні: «Діагональ прямокутника утворює два квадрати, у яких вертикальна і горизонтальна сторонни утворюють окремо». Це, напевне, перше формулювання теореми Піфагора (сам Піфагор народився, швидше за все, пізніше, вже після того, як була написана «Сульвасутра»; давньогрецькі формулювання і доведення його теореми, ті, що збереглися, відносяться до більш пізньої епохи).
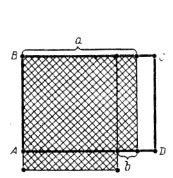
Побудова, описана в книзі «Сульвасутра», далеко не найпростіша. Більш просте розв’язання видно з мал: якщо хорда CD, перпендикулярна діаметру АВ, перетинає його в точці О, то CО2 = CO . OD =АО . ОВ
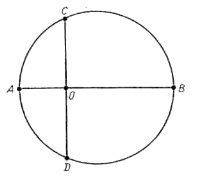
В, тобто СО — сторона квадрата, площа якого дорівнює площі прямокутника із сторонами АО і ОВ. Евклід описує саме таку побудову, але доведення у нього таке саме, як в книзі «Сульвасутра»; воно теж основане на теоремі Піфагора.
Візьмемо на продовженні сторони ВС за точку В таку точку Е, що ВЕ=АВ. Нехай О—середина відрізка ЕС, Р—точка перетину променя АВ і кола з діаметром ЕС. Евклід доводить, що площа квадрата із стороною ВР рівна площі прямокутника АBCD,наступним міркуванням. Площа прямокутника ABCD рівна площі заштрихованої фігури. Отже, вона рівна різниці площ квадратів із сторонами ЕО = ОР і ВО. За теоремою Піфагора площа квадрата, побудованого на катеті ВР прямокутного трикутника ОВР, дорівнює різниці площ квадратів, побудованих на гіпотенузі ОР і катеті ВО.
Таке дивне доведення Евкліда важко пояснити. Теорема про те, що CO . OD = AO . OB (див. попередній мал.), йому відома, причому доводить він її, спираючись теж фактично лише на теорему Піфагора (не використовуючи дуже складної теорії відношень). В усякому разі, збіг давньогрецького і давньоіндійського доведень навряд чи випадковий.
* * *
Найдавніші, що дійшли до нас давньогрецькі розв’язання задачі про квадратуру круга на перший погляд здаються просто дурістю. Афінянин Антифонт вписував в круг многокутник (трикутник або квадрат), потім ділив дуги навпіл і будував вписаний мнокутник з подвоєним числом сторін і т.д. Він думав, що врешті-решт вийде багатокутник, який, завдяки дуже малій довжині своїх сторін, співпаде з колом. Брізон узяв квадрат, вписаний в круг, і квадрат, описаний навколо круга, а потім узяв квадрат, що лежить між ними. Він стверджував, що площа останнього квадрата рівна площі круга.
Пізніші давньогрецькі коментатори до розв’язків Антифонта і Брізона відносилися зневажливо і їх взагалі не обговорювали. Але діяльність Антифонта і Брізона не слід недооцінювати. Для розв’язання задачі квадратури круга необхідно було зрозуміти, що ж таке площа круга, а для цього було потрібно мати уявлення про межу. В Стародавній Індії обійшли ці труднощі, ухваливши на віру неточне розв’язання цієї задачі. Антифонт і Брізон навмання шукали поняття межі. В їх міркуваннях невірного багато, але є і дещо дуже важливе; створений згодом метод виключеннч багато що у них перейняв. Архімед при обчисленні числа П як відношення довжини кола до діаметра використовував як ідею Антифонта (перехід від вписаного n-кутника до вписаного 2n-кутника), так і ідею Брізона (застосування не тільки вписаних, але і описаних многокутників).
Розв'язування олімпіадних задач.
Задача 1.
Доки лисиця робить п’ять стрибків, собака робить три, але відстань, яку собака долає за чотири стрибки, лисиця долає за десять. Визначити відношення швидкостей собаки та лисиці.
Розв’язання
Нехай швидкості собаки та лисиці відповідно дорівнюють vc та vл. Час, за який лисиця робить 5 стрибків, а собака 3, дорівнює t. Тоді на один стрибок лисиця витрачає ![]() , а собака
, а собака ![]() . Отже, на 10 стрибків лисиця витратить 10 •
. Отже, на 10 стрибків лисиця витратить 10 • ![]() = 2t, а собака 4 •
= 2t, а собака 4 • ![]() =
= ![]() . Знайдемо відношення швидкостей: vc : vл =
. Знайдемо відношення швидкостей: vc : vл =  =
= ![]() .
.
Відповідь. 3 : 2.
Задача 2.
Відомо, що ![]() - ціле, довести що
- ціле, довести що ![]() також ціле.
також ціле.
Розв’язання
![]() = (
= (![]() )2 - 2 . Оскільки права частина цієї тотожності є цілою, то і ліва є також цілою.
)2 - 2 . Оскільки права частина цієї тотожності є цілою, то і ліва є також цілою.
Задача 3.
Розв’язати систему рівнянь
х + у + ху = 11,
![]() х2 + ху + у2 = 19.
х2 + ху + у2 = 19.
Розв’язання
![]() Позначимо х + у = а, xy = b. Матимемо:
Позначимо х + у = а, xy = b. Матимемо:
a + b = 11,
a2 – b = 19;
![]() a + b = 11,
a + b = 11,
a2 + a – 30 = 0;
![]()
![]() a = -6,
a = -6,
b = 17;
![]() a = 5,
a = 5,
b = 6;
Повернемося до змінних х та у
![]()
![]() x + y = -6,
x + y = -6,
xy = 17;
![]() x + y = 5,
x + y = 5,
xy = 6;
Перша система сукупності не має розв’язку. З другої системи отримуємо дві пари чисел: (2; 3), (3; 2).
Відповідь: (2; 3), (3; 2).
Задача 4
Розв’язати рівняння х4 –2х3 + х2 + у2 - 4у + 4 = 0
Розв’язання
х4 –2х3 + х2 + у2 - 4у + 4 = 0,
![]() (х2 – х)2 + (у – 2)2 = 0,
(х2 – х)2 + (у – 2)2 = 0,
![]() x = 0,
x = 0,
![]()
![]() x = 0, y = 2;
x = 0, y = 2;
![]()
![]() х2 – х = 0 x = 1; x = 1,
х2 – х = 0 x = 1; x = 1,
у – 2 = 0, y = 2; y = 2.
Відповідь. (0; 2) та (1; 2)
Задача 5
У трикутнику АВС на стороні АВ взято точку D таку, що ![]() . Довести, що кут С тупий.
. Довести, що кут С тупий.
Розв’язання
За теоремою синусів маємо:
![]()
З цих пропорцій випливає: sin ACD = sin ACB . Але це можливо лише за умови, що один із цих кутів тупий. Отже, ![]() C—тупий.
C—тупий.
Задача 6.
Розв’яжіть систему рівнянь: 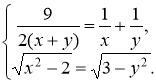
Розв’язання
Спочатку окремо розглянемо перше рівняння при ![]() :
: ![]()
![]()
![]()
![]()
![]()
![]() , тобто
, тобто ![]() та
та ![]() .
.
Таким чином усі пари ![]() та
та ![]() при
при ![]() задовольняють перше рівняння.
задовольняють перше рівняння.
Тепер перевіримо, які із знайдених розв’язків задовольняють друге рівняння. Для цього повинна одночасно виконуватись три умови: ![]() ,
, ![]() ,
, ![]() . Якщо підставити пару
. Якщо підставити пару ![]() у першу умову, маємо:
у першу умову, маємо: ![]() або
або ![]() звідки
звідки ![]() , тобто отримали пари
, тобто отримали пари ![]() та
та ![]() . Але вони не задовольняють умову
. Але вони не задовольняють умову ![]() , а тому не є розв’язками. Аналогічно підставимо пару
, а тому не є розв’язками. Аналогічно підставимо пару ![]() у перше рівняння і одержимо
у перше рівняння і одержимо ![]()
![]()
![]() , звідки маємо такі пари можливих розв’язків системи
, звідки маємо такі пари можливих розв’язків системи ![]() та
та ![]() . Перевіркою, переконуємось, що вони і є
. Перевіркою, переконуємось, що вони і є
Відповідь: ![]() та
та ![]() .
.
Задача 7.
Знайти найменше натуральне число, добуток цифр якого складає ![]() .
.
Розв’язання
Оскільки ![]() , то найголовніше запитання – яку найменшу кількість цифр повинно мати це число. Очевидно, що серед цифр числа немає
, то найголовніше запитання – яку найменшу кількість цифр повинно мати це число. Очевидно, що серед цифр числа немає ![]() , а також зрозуміло, що це число повинно мати цифру
, а також зрозуміло, що це число повинно мати цифру ![]() , бо це єдина цифра окрім
, бо це єдина цифра окрім ![]() , яка кратна
, яка кратна ![]() . З шести множників
. З шести множників ![]() щонайменше утворити дві цифри –
щонайменше утворити дві цифри – ![]() . Залишається з цифр
. Залишається з цифр ![]() утворити найменше число. Очевидно, що шукане найменше число – це
утворити найменше число. Очевидно, що шукане найменше число – це ![]() .
.
Відповідь: ![]() .
.
Задача 8.
Довести, що для будь-яких дійсних чисел ![]() справджується нерівність:
справджується нерівність:
![]() .
.
Розв’язання
Зробимо заміну: ![]() та
та ![]() і нерівність набуває вигляду:
і нерівність набуває вигляду: ![]() , яка очевидно виконується. Зрозуміло, що при будь-яких знаках
, яка очевидно виконується. Зрозуміло, що при будь-яких знаках ![]() існують відповідні
існують відповідні ![]() . Крім того, задача розв’язується простими піднесеннями до квадрату.
. Крім того, задача розв’язується простими піднесеннями до квадрату.
Задача 9.
Задано трикутник ![]() та точка
та точка ![]() , яка не належить жодній з прямих, які містять сторони трикутника. Нехай
, яка не належить жодній з прямих, які містять сторони трикутника. Нехай ![]() – пряма, яка проходить через точку
– пряма, яка проходить через точку ![]() перпендикулярно до прямої
перпендикулярно до прямої ![]() ,
, ![]() . Нехай
. Нехай ![]() є точкою перетину прямих
є точкою перетину прямих ![]() ,
, ![]() – точка перетину прямих
– точка перетину прямих ![]() , а точка
, а точка ![]() є перетином прямих
є перетином прямих ![]() , а точки
, а точки ![]() –точки перетину висот трикутників
–точки перетину висот трикутників ![]() ,
, ![]() ,
, ![]() відповідно. Довести, що трикутники
відповідно. Довести, що трикутники ![]() та
та ![]() рівні.
рівні.
Розв’язання
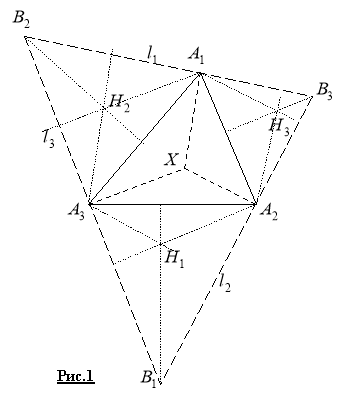
Маємо, що ![]() , як прямі, перпендикулярні до
, як прямі, перпендикулярні до ![]() , аналогічно
, аналогічно ![]() , тому
, тому ![]() паралелограм. Так само показуємо, що
паралелограм. Так само показуємо, що ![]() та
та ![]() також паралелограми. Тому
також паралелограми. Тому ![]() та
та ![]() – рівні та паралельні, звідки
– рівні та паралельні, звідки ![]() – паралелограм, тобто
– паралелограм, тобто ![]() . Аналогічно міркування проводимо для інших сторін трикутників. Тому
. Аналогічно міркування проводимо для інших сторін трикутників. Тому ![]() та
та ![]() рівні за трьома сторонами.
рівні за трьома сторонами.
 Задача 10.
Задача 10.
Шахівниця розміром ![]() пофарбована у шаховому порядку (усі кутові клітини чорні). По шахівниці ходить фішка, яка може ходити з клітини на сусідню по стороні клітину. Якщо фішка попадає на деяку клітину, то ця клітина змінює свій колір на протилежний. На початку фішка стоїть у лівому нижньому куті. Чи можна за допомогою цієї фішки перефарбувати усі клітини дошки у чорний колір, якщо ходити відразу у зворотному напрямі заборонено? Тобто, ходити як на рис.2 недозволено, а як на рис.3 можна.
пофарбована у шаховому порядку (усі кутові клітини чорні). По шахівниці ходить фішка, яка може ходити з клітини на сусідню по стороні клітину. Якщо фішка попадає на деяку клітину, то ця клітина змінює свій колір на протилежний. На початку фішка стоїть у лівому нижньому куті. Чи можна за допомогою цієї фішки перефарбувати усі клітини дошки у чорний колір, якщо ходити відразу у зворотному напрямі заборонено? Тобто, ходити як на рис.2 недозволено, а як на рис.3 можна.
Розв’язання
Оскільки у нас усі кутові клітини чорні покажемо шлях, як можна у чорний колір пофарбувати усі інші клітини.
На рис.4 показано, як можна пройти шлях від будь-якої клітини до деякої фіксованої клітини, яка розташована не у куту дошки. Ця клітина на рис.8 середня у верхньому ряду. Далі маршрут проходить зворотнім шляхом, як бачимо нема жодного ходу назад, і кожна клітина, крім обраної фарбується парну кількість разів (усі по 2 рази і одна – 4 рази), тобто не змінює свій колір. Перед останнім кроком ми дивимось на колір початкового поля. Якщо воно біле, то ми ставимо фішку у це поле і вся дошка стає чорною, інакше – ми не заходимо у нього і так само уся дошка – чорна.

Відповідь: Можна.
3. Нерівності
Раціональні нерівності зі змінною.
Розв'язати нерівність — це означає вказати всі дійсні значення невідомих, для яких ця нерівність справджується.
Для розв'язування нерівностей виду (х – а1)(х - а2)(х – а3)...(х — ап) > < 0 застосовується метод інтервалів. Нагадаємо теорему.
Теорема. Якщо функція f (х) визначена і неперервна на даному проміжку і не має на ньому нулів, то при всіх значеннях х, що належать даному проміжку, функція f (х) зберігає знак.
Наведемо алгоритм застосування методу інтервалів для розв'язування нерівностей.
1. Знаходимо корені многочлена (х – а1)(х - а2)(х – а3)...(х — ап).
2. Відкладаємо знайдені значення коренів многочлена на числовій прямій.
3. Знаходимо знак алгебраїчного виразу на одному з інтервалів.
4. Якщо немає кратних коренів, то знаки чергуються.
5. Записуємо відповідь.
Приклад 1.
Розв'язати нерівність:
(х — 8)(х — 3)(2х + 1) < 0.
Розв'язання.
На числовій осі відкладаємо корені многочлена f (х) = (х - 8)(х - 3)(2х + 1), х1 = 8, х2 = 3, х3 = -![]() . Визначаємо знак многочлена f(x) на одному з утворених проміжків.
. Визначаємо знак многочлена f(x) на одному з утворених проміжків.
На проміжку (-![]() ; 3) f (х) > 0. На решті проміжків знаки чергуються
; 3) f (х) > 0. На решті проміжків знаки чергуються
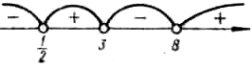
Записуємо відповідь.
Відповідь. 3 < х < 8, х < - ![]()
Приклад 2.
Розв'язати нерівність;
(х - 2)10(х + 3)17(х + 1)5(х2 + 3)17 > 0.
Розв'язання.
Перепишемо нерівність у вигляді
(х - 2)10(х + 3)(х + 3)16(х + 1)(х + 1)4 (x2 + 3)17 > 0.
Дана нерівність рівносильна системі
x ![]() 2
2
х ![]() -3
-3
х ![]() - 1
- 1
(х + 3)(х + 1) > 0,
![]() (оскільки при х
(оскільки при х ![]() 2, х
2, х ![]() -3, х
-3, х ![]() -1, обидві частини нерівності можна розділити на додатний многочлен (х - 2)10(х + 3)16(х + 1)4(x2 + 3)17).
-1, обидві частини нерівності можна розділити на додатний многочлен (х - 2)10(х + 3)16(х + 1)4(x2 + 3)17).
Розв'язуючи цю нерівність методом інтервалів, дістанемо
х < -3, -1 < х < 2, х > 2.
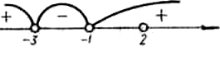
Відповідь. х < -3, - 1 < х < 2, х > 2.
Приклад 3.
Розв'язати нерівність:
![]() .
.
Розв'язання.
Запишемо нерівність в такому вигляді
![]() .
.
Після перетворень маємо:
![]() 0.
0.
Утворена нерівність рівносильна системі
![]() (х - 3)(x - 1)(x + 1)
(х - 3)(x - 1)(x + 1) ![]() 0.
0.
x ![]() -1
-1
x ![]() 1
1
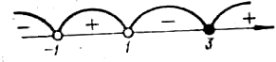
Розв'язуємо цю нерівність методом інтервалів.
Відповідь. x < -1, 1 < х ![]() 3.
3.
Для розв'язування квадратних нерівностей, дискримінант квадратного тричлена яких менший за .нуль, доцільно користуватися правилом, яке випливає, з графічного дослідження квадратного тричлена.
Якщо дискримінант квадратного, тричлена менший за нуль, то знак квадратного тричлена збігається із знакoм коефіцієнта при х2.
Якщо дискримінант квадратного тричлена не менший за нуль, то, розклавши його на лінійні множники, розв'язуємо нерівність методом інтервалів.
Приклад 4.
Розв'язати нерівність:
![]()
Розв'язання.
Оскільки дискримінанти тричленів 3х2 - 2х + 4 та х2 + 3х + 4 від'ємні, то їх знаки збігаються з коефіцієнтами при х2. Отже, 3х2 - 2х + 4 >0 та х2 + 3х + 4 > 0.
Таким чином, дана нерівність рівносильна нерівності
х2 - х - 6 ![]() 0, (х - 3)(х + 2)
0, (х - 3)(х + 2) ![]() 0. Звідки - 2
0. Звідки - 2 ![]() х
х ![]() 3.
3.
Відповідь. —2 ![]() х
х ![]() 3.
3.
Метод інтервалів. Нерівності з параметрами.
Розв'язуючи раціональні нерівності та дробово-раціональні нерівності з параметрами, можна використовуючи метод інтервалів. Суть цього методу полягає в наступному.
Нехай дано нерівність f(x) > а або f(x) < а. Для її розв'язування поступаємо так:
1) вводимо функцію F(х, а) так, щоб нерівність мала вигляд: F(x, а) > 0 або F(x, a) < 0;
2) знаходимо корені рівняння F(x, а) = 0, які залежать від параметра а;
3) з'ясовуємо, як корені розміщені на числовій осі залежно від значень параметра;
4) наносимо корені на числову вісь і вказуємо, для якого значення параметра справедливе таке розміщення;
5) досліджуємо знак виразу F(x, a) на кожному проміжку числової прямої;
6) записуємо відповіді залежно від даної в умові нерівності.
Застосовувати метод інтервалів до розв'язування раціональних нерівностей з параметрами можна на факультативних заняттях.
1. Цілі раціональні нерівності вищих порядків.
Слід розглянути раціональні нерівності вищих порядків для двох-випадків:
1) якщо коефіцієнти при змінних у співмножниках не залежать від параметра;
2) якщо коефіцієнти при змінних у співмножниках залежать від параметра.
Приклад 1. Розв'язати нерівність
(х - а)3(х + 1)5(х - (2а +1)) < 0.
Розв'язання
Введемо функцію
F(x, a) = (х - а)3(х + 1)5(х -(2а + 1)).
Розв'яжемо рівняння
(х - а)3(х + 1)5(x - (2а +1)) = 0,
звідки
х1= а, х2 = -1, х3 = 2а + 1.
Порівняємо корені х1, х2 і х3. Для цього складемо різниці:
A1 = х1 - х2 = а +1,
А2 = х1 - х3 = -а - 1,
А3 = х2 - х3 = -2а - 2.
Для а > — 1 маємо: А1 > 0, А2 < 0, А3 < 0, тобто х2 < х1 < х3, а для а < -1 отримаємо: А1 < 0, А2 > 0, А3 > 0, тобто х3 < х1 < х2.
Тому для а < -1 маємо такі розміщення коренів та знаки функції F(x, а) на відповідних проміжках, як показано на малюнку.
![]()
Ситуацію для а > — 1 показано на наступному малюнку.
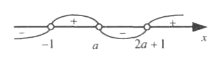
Для а = - 1 одержимо:
(х + 1)9 < 0, х < -1.
Відповідь. Якщо а є (-![]() ; -1], то x є (-
; -1], то x є (-![]() ; 2a + l) U (a; -l); якщо а є (-1; +
; 2a + l) U (a; -l); якщо а є (-1; + ![]() ), то х є (-
), то х є (-![]() ; -1) U (а; 2а +1).
; -1) U (а; 2а +1).
Приклад 2. Розв'язати нерівність
((а + 3)х + а)(2х - а)3 (![]() - (а + 5))
- (а + 5)) ![]() 0.
0.
Розв'язання
Для а = -3 маємо: -3(2х + 3)3(![]() - 2)
- 2) ![]() 0,
0,
(2х + 3)3(х - 4) ![]() 0
0
і знаки функції F(х; а) будуть такими, як показано на малюнку.
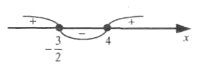
Розглянемо випадок, коли а ![]() -3 .
-3 .
Знайдемо корені рівняння:
((а + 3)х + а)(2х - а)3 (![]() - (а + 5))= 0 ,
- (а + 5))= 0 ,
x1 = -![]() , x2 = -
, x2 = -![]() , х3 = 2a +10 .
, х3 = 2a +10 .
Порівняємо корені х1, х2 і х3. Для цього складемо різниці:
A1 = x1 – x2 = -![]() -
- ![]() = -
= - ![]() ,
,
A2 = x1 – x3 = -![]() - (2a + 10) = -
- (2a + 10) = - 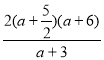 ,
,
A3 = x2 – x3 = -![]() - (2a+10) = -
- (2a+10) = -![]() a – 10.,
a – 10.,
Порівняємо значення коренів х1, х2, х3 на проміжках, на які розбивають числову вісь числа, що перетворюють у нуль значення виразів A1, A2, А3, або для яких вирази А1, А2, А3 не існують. Такими є числа, зображені на малюнку.
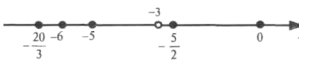
Для а є (0; +![]() ) : х1 < х2 < х3.
) : х1 < х2 < х3.
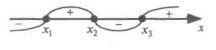
Для а є (-![]() ; 0) : х2 < х1 < х3.
; 0) : х2 < х1 < х3.
![]()
Для а є (-3; -![]() ) : х2 < х3 < х1.
) : х2 < х3 < х1.
![]()
Для а є (-5; - 3): х1 < х2 < х3.
![]()
Для а є (-6; -5): х2 < х1 < х3.
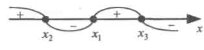
Для а є (-![]() ; -6): х2 < х3 < х1.
; -6): х2 < х3 < х1.
![]()
Для а є (-![]() ; -
; -![]() ): х3 < х2 < х1.
): х3 < х2 < х1.
![]()
Для а = 0 маємо:
![]() , х є (-
, х є (-![]() ; 10].
; 10].
Для а = -![]() маємо:
маємо:
(x - 5)2( 2x - ![]() )3
)3 ![]() 0, х є (-
0, х є (-![]() ;
; ![]() )
) ![]() {5}.
{5}.
Для а = -5 маємо:
![]() (2х + 5)4 > 0, х є [0; +
(2х + 5)4 > 0, х є [0; +![]() )
) ![]() {
{![]() }.
}.
Для а = -6 маємо:
(2х + 6)3(х + 2)2 ![]() 0, х є [-3; +
0, х є [-3; +![]() ).
).
Для а = - ![]() маємо:
маємо:
(-11х - 20)(3х + 10)4 ![]() 0, х є
0, х є ![]() {-
{-![]() }.
}.
Відповідь. Якщо а є (0; +![]() ), то
), то ![]() ;
;
Якщо а є ![]() , то
, то ![]() ;
;
Якщо а є ![]() , то
, то ![]() ;
;
Якщо а є (-5;-3), то ![]() ;
;
Якщо а є (-6; 5], то ![]() ;
;
Якщо а є ![]() , то
, то ![]() ;
;
Якщо а є ![]() , то
, то ![]() ;
;
Якщо а = -3, то ![]() .
.
Приклад 3. Розв'язати нерівність
(ах - (а + 1))3((а + 1)х - (а - 6))((а - 1)х - а)7 ![]() 0.
0.
Розв'язання
Для а = 0 маємо:
-(х + 6)(-х - 0)7 ![]() 0, х Є (-
0, х Є (-![]() ; -6] U [0; +
; -6] U [0; +![]() ).
).
Для а = - 1 маємо:
-х3(-2х + 1)7 ![]() 0, х є (-
0, х є (-![]() ; 0] U
; 0] U ![]() .
.
Для а = 1 маємо:
-(х - 2)3(2х + 5) ![]() 0 , х Є
0 , х Є ![]() .
.
Розглянемо випадок, коли а ![]() 0, а
0, а![]() -1, а
-1, а ![]() 1. Знайдемо корені многочлена F(x; а) = (ах - (а + 1))3((а + 1)х - (а - 6))((а - 1)х - а)7.
1. Знайдемо корені многочлена F(x; а) = (ах - (а + 1))3((а + 1)х - (а - 6))((а - 1)х - а)7.
Для цього розв'яжемо рівняння:
(ах - (а + 1))3((а + 1)х - (а - 6))((а - 1)х - а)7 = 0,
х1 = ![]() ; х2 =
; х2 = ![]() ; х3 =
; х3 = ![]() .
.
Порівняємо корені х1, х2 і х3 . Для цього складемо різниці:
А1 = х1 - х2 = ![]() -
- ![]() =
= ![]() ;
;
А2 = х1 - х3 = ![]() -
- ![]() =
= ![]() ;
;
А3 = х2 - х3 = ![]() -
- ![]() =
= ![]() .
.
Дослідимо знаки виразів А1, А2, А3 на проміжках, на які розбили числову вісь числа, для яких вирази A1, А2, А3 перетворюються в нуль або не існують.

Для а є (1; +![]() ): х2 < х1 < х3.
): х2 < х1 < х3.
![]()
Для а є (![]() ; 1): х3 < х2 < х1.
; 1): х3 < х2 < х1.
![]()
Для а є (0; ![]() ): х2 < х3 < х1.
): х2 < х3 < х1.
![]()
Для а є (-![]() ; 0): х1 < х2 < х3.
; 0): х1 < х2 < х3.
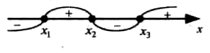
Для а є (-1; -![]() ;): х2 < х1 < х3.
;): х2 < х1 < х3.
![]()
Для а є (-![]() ; -1): х1 < х3 < х2.
; -1): х1 < х3 < х2.
![]()
Для а = ![]() :
:
(3х - 7)3(х + 3)8 ![]() 0, х Є
0, х Є ![]() .
.
Для а = -![]() :
:
(х + 7)4(9х - 1)7 ![]() 0, х Є
0, х Є ![]() .
.
Відповідь. Якщо а є (1; +![]() ), то
), то ![]() ;
;
Якщо а є (![]() ; 1), то
; 1), то ![]() ;
;
Якщо а є (0; ![]() ), то
), то ![]() ;
;
Якщо а є (-![]() ; 0), то
; 0), то ![]() ;
;
Якщо а є (-1; -![]() ], то
], то ![]() ;
;
Якщо а є (![]() ; -1), то
; -1), то ![]() ;
;
Якщо а = -1, то ![]() ;
;
Якщо а = 0, то ![]() ;
;
Якщо а = 1, то ![]() .
.
2. ДРОБОВО-РАЦІОНАЛЬНІ НЕРІВНОСТІ
Метод інтервалів можна використовувати і для розв'язування дробово-раціональних нерівностей з параметрами, але відмінність полягатиме у врахуванні області визначення. Пропонуємо нерівність, для розв'язування якої використовується властивість коренів квадратного тричлена, а також нерівність, область визначення якої залежить від параметра а.
Приклад 4. Розв'язати нерівність
![]() .
.
Розв'язання
Область визначення даної нерівності — множина всіх дійсних чисел, крім х = 0.
Перетворимо дану дробово-раціональну нерівність у рівносильну на області визначення:
![]() ,
,
![]()
![]()
![]()
х((а - 5)х2 + 5х - 4) < 0.
Введемо функцію
F(x; а) = х(х2(а - 5) + 5х - 4).
Для а = 5 маємо:
х(5х - 4) < 0, х є ![]() ;
;
Для а ![]() 5 знайдемо нулі функції F(х; а):
5 знайдемо нулі функції F(х; а):
![]() х(х2(а - 5) + 5х - 4) = 0,
х(х2(а - 5) + 5х - 4) = 0,
х = 0,
х2(а - 5) + 5х - 4 = 0.
Окремо розглянемо рівняння
х2(а - 5) + 5х - 4 = 0.
Знайдемо дискримінант цього рівняння:
D = 25 + 16(а — 5) = 16а - 55.
Для D = 16а — 55 < 0, тобто для a < ![]() рівняння не має коренів.
рівняння не має коренів.
Для D = 0, тобто для а = ![]() рівняння має два корені, що збігаються.
рівняння має два корені, що збігаються.
Для D = 16а — 55 > 0, тобто для а > ![]() рівняння має два різні корені:
рівняння має два різні корені:
x1 = ![]() ; х2 =
; х2 = ![]() .
.
Для а < ![]() маємо:
маємо:
х2(а - 5) + 5х - 4 < 0
для всіх х є R .
Тоді
х(х2(а - 5) + 5х - 4) < 0,
коли х > 0.
Для а = ![]() маємо:
маємо:
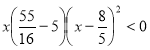 ,
,
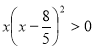 , якщо х > 0 і х
, якщо х > 0 і х ![]()
![]() .
.
Розглянемо випадок, коли а > ![]() .
.
Функція F(х; а) має вигляд: F(x; а) = х(а - 5)(х – х1)(х - х2) .
Визначимо взаємне розміщення коренів х1, х2 і числа х3 = 0. Для цього скористаємося властивістю коренів квадратного тричлена
(а - 5)х2 + 5х - 4 .
З'ясуємо, для яких а корені х1 та х2 додатні:
(a - 5)f(x3) > 0,
![]() x3 < -
x3 < -![]() ,
,
(a - 5)(-4) > 0,
![]() 0 < -
0 < -![]() ,
,
a < 5.
Отже, для а Є (![]() ; 5) маємо:
; 5) маємо:
х3 < х2 < х1.
Розмістимо числа х1, х2, х3 на числовій прямій і визначимо знак функції F(х; а) на утворених проміжках.
![]()
З'ясуємо, для яких значень а корені х1 та х2 лежать по різні боки від числа х3 = 0. Для цього має виконуватися умова:
(а - 5)f(х3) < 0,
звідки а > 5.
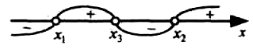
З'ясуємо, для яких значень а корені х1 та х2 від'ємні, тобто лежать зліва від числа х3 = 0. Для цього мають виконуватися умови:
![]() (a - 5)f(x3) > 0,
(a - 5)f(x3) > 0,
x3 > -![]() ,
,
![]() (-4)(a - 5) > 0,
(-4)(a - 5) > 0,
(-5)(2a – 10)<0,
![]() a < 5,
a < 5,
a > 5.
Отже, таких значень а не існує.
Відповідь. Якщо а Є ![]() , то х Є (0; +
, то х Є (0; +![]() );
);
Якщо а Є ![]() , то х Є (0;
, то х Є (0; ![]() )
) ![]() (
(![]() );
);
Якщо а Є ![]() , то х Є (-
, то х Є (-![]() ;
; ![]() )
) ![]() (0;
(0; ![]() );
);
Якщо а = 5, то х Є (0; ![]() ).
).
Приклад 5. Розв'язати нерівність
![]() +
+ ![]() <
< ![]() .
.
Розв'язання
Область визначення нерівності знаходимо з умови, що х![]() а. Перетворимо дану дробово-раціональну нерівність:
а. Перетворимо дану дробово-раціональну нерівність:
![]() +
+ ![]() <
< ![]() ,
,
![]() +
+ ![]() -
- ![]() < 0,
< 0,
(а2 - х2)((3a - 1)х + (3а2 - а)) < 0,
(3a - 1)( x - a)(x + a)2 > 0.
Введемо функцію
F(x; а) = (3а - 1)(х - а)(х + а)2.
Для а =![]() — отримаємо, що 0 > 0, тобто нерівність не має розв'язку.
— отримаємо, що 0 > 0, тобто нерівність не має розв'язку.
Для а ![]()
![]() - знайдемо нулі функції F(х; а):
- знайдемо нулі функції F(х; а):
(3a - 1)(x - a)(x + a)2 = 0,
x1 = а, х2 = -а .
Порівняємо корені х1 і х2. Для цього складемо різницю
A = x1 - x2 = 2a .
Для a > 0 вираз A = x1 - x2 > 0, тобто х1 > x2.
Для а є (0; ![]() ) знаки функції F (x; а) на відповідних проміжках будуть такими, як показано на малюнку.
) знаки функції F (x; а) на відповідних проміжках будуть такими, як показано на малюнку.
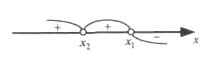
Знаки функції F(x; а) для а є (![]() ; +
; +![]() ) на наступному малюнку.
) на наступному малюнку.
![]()
Для а < 0 вираз A = х1 - х2 < 0 , тобто х1 < х2. Розмістимо корені х1 і х2 на числовій прямій і знайдемо знаки функції F(x; а) на відповідних проміжках.
![]()
Якщо а = 0, то х < 0.
Відповідь. Якщо а є (![]() ; +
; + ![]() ), то х є (а; +
), то х є (а; + ![]() );
);
якщо а є (-![]() ; 0], то x є (-
; 0], то x є (-![]() ; а);
; а);
якщо а є (0; ![]() ), то x є (-
), то x є (-![]() ; -а)
; -а) ![]() (-a; a);
(-a; a);
якщо а = ![]() , то нерівність розв’язків не має.
, то нерівність розв’язків не має.
Ірраціональні нерівності.
Ірраціональними нерівностями називаються нерівності, які містять змінну під знаком кореня або під знаком степеневої функції з дробовим показником.
Розв'язування ірраціональних нерівностей зводиться до розв'язування рівносильних нерівностей, систем раціональних нерівностей, їх сукупності, або за загальним методом.
При розв'язуванні найпростіших ірраціональних нерівностей виду
![]() < g(x);
< g(x); ![]() > g(x);
> g(x); ![]() < g(x);
< g(x); ![]() > g(x) ; де f(х) і g(x) — раціональні функції, n є N, доцільно користуватися наступними твердженнями.
> g(x) ; де f(х) і g(x) — раціональні функції, n є N, доцільно користуватися наступними твердженнями.
Твердження 1. Нерівність ![]() < g(x) рівносильна нерівності f(x) < g2n+1 (x) .
< g(x) рівносильна нерівності f(x) < g2n+1 (x) .
Твердження 2. Нерівність ![]() > g(x) рівносильна нерівності f[x) > g2n+l (x) .
> g(x) рівносильна нерівності f[x) > g2n+l (x) .
Твердження 3. Нерівність ![]() < g(x) рівносильна системі нерівностей:
< g(x) рівносильна системі нерівностей:
![]() f (x)
f (x)![]() 0,
0,
g (x) > 0,
f (x) < g 2n (x).
Твердження 4. Нерівність![]() > g(x) рівносильна сукупності двох систем нерівностей:
> g(x) рівносильна сукупності двох систем нерівностей:
![]() f (x)
f (x)![]() 0,
0,
g (x) < 0,
![]() g (x)
g (x)![]() 0,
0,
f (x) > g 2n (x).
Приклад 1. Розв'яжемо нерівність
![]() < 8 – x.
< 8 – x.
Розв'язання
Дана нерівність рівносильна такій системі:
![]() x2 - 3x – 10
x2 - 3x – 10 ![]() 0,
0,
8 – х > 0,
х2 - 3х – 10 < (8 - x)2;
![]() (х + 2)(х - 5)
(х + 2)(х - 5) ![]() 0,
0,
х < 8,
х2 - 3х – 10 < 64 - 16х + х2;
![]() (х + 2)(х - 5)
(х + 2)(х - 5) ![]() 0,
0,
х < 8,
х < ![]() .
.
Звідси х ![]() -2 або 5
-2 або 5 ![]() х <
х < ![]() .
.
Відповідь. ![]()
Приклад 2. Розв'яжемо нерівність
![]() > х – 3.
> х – 3.
Розв'язання
![]()
![]() x2 + 4x – 5
x2 + 4x – 5 ![]() 0,
0,
х - 3 < 0;
![]() х - 3
х - 3 ![]() 0,
0,
x2 + 4x – 5 > (x – 3)2;
![]()
![]() (x + 5)(x – 1)
(x + 5)(x – 1) ![]() 0,
0,
х < 3;
![]() х
х ![]() 3,
3,
10x > 14;
![]()
![]()
![]() x
x ![]() -5,
-5,
х ![]() 1,
1,
х < 3;
![]() х
х ![]() 3,
3,
x > 1,4.
Відповідь. ![]()
Приклад 3. Розв'яжемо нерівність
(x - l) ![]()
![]() 0.
0.
Розв'язання
Оскільки другий множник у лівій частині нерівності невід'ємний і нерівність нестрога, то вона рівносильна такій сукупності:
![]()
![]() x – 1
x – 1 ![]() 0,
0,
х2 – х – 2 ![]() 0,
0,
x2 – х - 2 = 0.
![]()
![]() х
х![]() 1,
1,
(х + 1)(х - 2) ![]() 0,
0,
х = -1,
х = 2.
Звідси х ![]() 2 або х = -1.
2 або х = -1.
Відповідь. {-l} U [2; +![]() ).
).
Приклад 4. Розв'яжемо нерівність
![]() < 0.
< 0.
Розв'язання
Знаменник даної нерівності додатний, тому нерівність рівносильна такій системі:
![]() х – 7 < 0,
х – 7 < 0,
4x2 - 19х + 12 > 0;
![]() х<1,
х<1,
4(х - ![]() )(х - 4) > 0.
)(х - 4) > 0.
Відповідь. ( -![]() ;
; ![]() ) U (4; 7),
) U (4; 7),
Існує й загальний метод розв'язування нерівностей.
Метод інтервалів
Розв'яжемо нерівність f(х) < 0, або f (х) > 0, де f(x) — довільна функція.
1. Знаходимо область визначення функції D(f).
2. Визначаємо всі її нулі, тобто розв'язуємо рівняння f(x) = 0.
3. За допомогою знайдених коренів розбиваємо D(f) на проміжки знакосталості.
4. Визначаємо, який знак має функція f(x) на кожному з проміжків знакосталості. Знаходимо множину розв'язків даної нерівності.
Цей метод можна використовувати для розв'язування будь-яких нерівностей f (х) < 0, f (x) > 0, якщо можна знайти D (f), а також її нулі.
Приклад 5. Розв'яжемо нерівність
![]() >
> ![]() .
.
Розв'язання
Розглянемо функцію
f(x) =![]() -
- ![]() .
.
![]() Область визначення функції знайдемо з системи:
Область визначення функції знайдемо з системи:
х + 6 ![]() 0,
0,
х + 1 ![]() 0,
0,
2х – 5 ![]() 0;
0;
![]() х
х ![]() -6,
-6,
х ![]() -1,
-1,
х ![]() 2,5.
2,5.
Звідси х![]() 2,5.
2,5.
Знайдемо нулі функції, розв'язавши рівняння:
![]() =
= ![]()
x + 6 = x + l + 2![]() + 2x - 5,
+ 2x - 5,
10 - 2х =![]() ,
,
5 - х =![]() ,
,
25 - 10х + х2 = 2х2 - 3х - 5,
х2 + 7х - 30 = 0,
х1 = -10, х2 = 3.
Перевіркою встановлюємо, що х = 3 — корінь рівняння.
Розглянемо проміжки [2,5; 3), (3; +![]() ), на кожному з яких функція зберігає знак.
), на кожному з яких функція зберігає знак.
f(2,7) = ![]() > 0.
> 0.
f(10) = 4 - ![]() < 0. Отже, х є [2,5; 3).
< 0. Отже, х є [2,5; 3).
Відповідь. [2,5; 3).
Приклад 6. Розв'яжемо нерівність
![]() > 1.
> 1.
Розв'язання
Розглянемо функцію
f(x) = ![]() - 1.
- 1.
Область визначення функції знайдемо із системи:
![]() 3x2 + 5x + 7
3x2 + 5x + 7 ![]() 0,
0,
![]() х2 + 5х + 2
х2 + 5х + 2 ![]() 0;
0;
x є R
3(х + 1)(х + ![]() )
) ![]() 0.
0.
Звідси х ![]() -1 або х
-1 або х ![]() -
- ![]() .
.
Знайдемо нулі функції, розв'язавши рівняння
![]() = 1.
= 1.
![]() + 1,
+ 1,
3х2 + 5х + 7 = 3х2 + 5х + 2 + 1 + 2![]() ,
,
2 = ![]() ,
,
4 = 3х2 + 5х + 2,
3х2 + 5x – 2 = 0,
х1 = -2, х2 = ![]() .
.
Перевіркою можна встановити, що х1 = -2 і х2 = ![]() - корені рівняння.
- корені рівняння.
Розглянемо проміжки (-![]() ; -2), (-2; -1],
; -2), (-2; -1], ![]() ,
, ![]() , на кожному з яких функція зберігає знак.
, на кожному з яких функція зберігає знак.
f (-10) < 0, f (-1,5) > 0, f (0) > 0, f (10) < 0.
Розв'язками вихідної нерівності будуть значення х з проміжків, де f(x) > 0, тобто х є (-2; -l] U ![]()
Відповідь. (-2; -l] U ![]()
Приклад 7. Розв'яжемо нерівність
(х - 3)![]()
![]() х2 - 9.
х2 - 9.
Розв'язання
Розглянемо функцію
f(x) = (х - 3)![]() - (х2 – 9).
- (х2 – 9).
Область визначення функції — множина всіх дійсних чисел.
Знайдемо нулі функції f (х), розв'язавши рівняння
(х - 3)![]() - (х2 – 9) = 0.
- (х2 – 9) = 0.
(х - 3)(![]() - х – 3) = 0.
- х – 3) = 0.
![]() x - 3 = 0,
x - 3 = 0,
![]() - х – 3 = 0
- х – 3 = 0
![]() х = 3,
х = 3,
х2 + 4 = х2 + 6х + 9;
![]() х1 = 3
х1 = 3
x2 = -![]()
Перевіркою можна встановити, що х1 = 3 i x2 = -![]() - корені рівняння.
- корені рівняння.
Розглянемо проміжки ![]() [3; +
[3; +![]() ), на кожному з яких функція зберігає знак.
), на кожному з яких функція зберігає знак.
f (-10) < 0, f (0) > 0, f (10) < 0.
Розв'язками вихідної нерівності будуть значення х з проміжків, де f(x) ![]() 0, тобто x є
0, тобто x є ![]() [3; +
[3; +![]() ).
).
Відповідь. ![]() [3; +
[3; +![]() ).
).
Приклад 8.
Розв'язати нерівність:
(25 - х2) ![]()
![]() 0.
0.
Розв' язання.
Область визначення нерівності
х2— х— 12 > 0 (*)
x1= 4, х2 = —3. Розв язуючи нерівність (*), маємо х ![]() 4, х
4, х ![]() -3.
-3.
![]()
Другий множник даної нерівності невід'ємний, тому множину його розв'язків дістаємо як множину розв'язків систем нерівностей
![]()
![]() 25 - х2
25 - х2 ![]() 0 або х2 – 25
0 або х2 – 25 ![]() 0
0
х2 - х - 12 ![]() 0 х2 - х - 12
0 х2 - х - 12 ![]() 0.
0.
Розв'язуючи дану систему нерівностей, дістаємо 4 ![]() х
х ![]() 5, - 5
5, - 5 ![]() х
х ![]() -3.
-3.
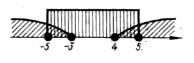
Відповідь. 4 ![]() х
х ![]() 5; -5
5; -5 ![]() х
х ![]() -3.
-3.
Приклад 9.
Розв'язати нерівність:
4 - х < ![]() .
.
Розв'язання.
Область визначення даної нерівності
х2 - 2х ![]() 0, х (х - 2)
0, х (х - 2) ![]() 0.
0.
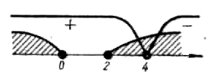
Звідки х ![]() 2 та х
2 та х ![]() 0.
0.
Розглянемо випадки:
1. 2 ![]() х
х ![]() 4 та х
4 та х ![]() 0. Обидві частини нерівності невід'ємні, тому після піднесення їх до квадрата, дістаємо рівносильну нерівність
0. Обидві частини нерівності невід'ємні, тому після піднесення їх до квадрата, дістаємо рівносильну нерівність
(4 - х)2 < х2 - 2х, або 16 - 8х + х2 < х2 - 2х, звідки х > ![]() .
.
![]()
![]() Отже, множина розв'язків нерівності рівносильна сукупності систем
Отже, множина розв'язків нерівності рівносильна сукупності систем
2 ![]() х
х ![]() 4 та х
4 та х ![]() 0
0
х > ![]() х >
х > ![]()
розв'язуючи які, знаходимо ![]() < х
< х ![]() 4.
4.
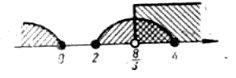
2. х > 4. Ліва частина нерівності від'ємна, а права — додатна.Тому нерівність справджується при будь-якому значенні х, що належить даному проміжку, х > 4.
Поєднуючи отримані розв'язки: х > 4 та ![]() < х
< х ![]() 4, маємо х >
4, маємо х > ![]() .
.
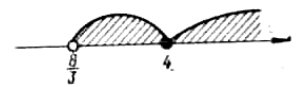
Приклад 10.
Розв'язати нерівність:
3![]() > 4х - 2.
> 4х - 2.
Розв' язання.
Знаходимо область визначення даної нерівності. Маємо:
6 + х - х2 ![]() 0, або х2 – х - 6
0, або х2 – х - 6 ![]() 0. (*)
0. (*)
Оскільки х1 = 3, х2 = -2 — корені квадратного тричлена х2 - х - 6, то розв'язком нерівності (*) є -2 ![]() х
х ![]() 3 .
3 .
![]()
Розглянемо усі можливі випадки.
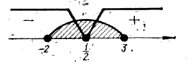
1. -2 ![]() х
х ![]()
![]() . Ліва частина нерівності невід'ємна, а права — від'ємна. Тому нерівність-виконується при будь-якому значенні х, що належить проміжку, тобто -2
. Ліва частина нерівності невід'ємна, а права — від'ємна. Тому нерівність-виконується при будь-якому значенні х, що належить проміжку, тобто -2 ![]() х
х ![]()
![]() .
.
2. -![]() < х
< х ![]() - 3. Обидві частини нерівності невід'ємні, тому після піднесення до квадрата дістаємо рівносильну нерівність:
- 3. Обидві частини нерівності невід'ємні, тому після піднесення до квадрата дістаємо рівносильну нерівність:
9 (6 + х — х2) > (4х — 2)2,
54 + 9х — 9х2 > 16х2— 16х + 4, :
х2— х — 2 < 0.
Корені квадратного тричлена х2 - х - 2 дорівнюють х1 = 2, х2 = -1.
Розв'язком даної нерівності на розглядуваному числовому проміжку є ![]() < х < 2.
< х < 2.
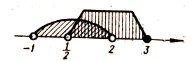
Поєднуючи отримані результати - 2 ![]() х
х ![]()
![]() та
та ![]() < x < 2, дістанемо — 2
< x < 2, дістанемо — 2 ![]() х < 2.
х < 2.
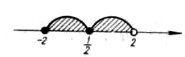
Приклад 11.
Розв'язати нерівність:
![]() > 1.
> 1.
Розв'язання.
![]() Знайдемо область визначення даної нерівності.
Знайдемо область визначення даної нерівності.
х + 3 ![]() 0
0
2 – х ![]() 0.
0.
Маємо -3 ![]() х
х ![]() 2.
2.
Запишемо дану нерівність у вигляді ![]() . Обидві частини даної нерівності невід'ємні, тому, підносячи їх до квадрата, дістаємо нерівність, рівносильну даній.
. Обидві частини даної нерівності невід'ємні, тому, підносячи їх до квадрата, дістаємо нерівність, рівносильну даній.
![]() ,
,
х > ![]() .
.
Розглянемо такий проміжок і всі можливі випадки.
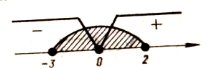
1. -3 ![]() х
х ![]() 0. Ліва частина нерівності від'ємна, а права — додатна. Тому для будь-якого значення х із розглядуваного проміжку нерівність не виконується.
0. Ліва частина нерівності від'ємна, а права — додатна. Тому для будь-якого значення х із розглядуваного проміжку нерівність не виконується.
2. 0 < х ![]() 2. Обидві частини нерівності невід'ємні, тобто після піднесення до квадрата дістаємо рівносильну нерівність
2. Обидві частини нерівності невід'ємні, тобто після піднесення до квадрата дістаємо рівносильну нерівність
![]() х2 > 2 - х
х2 > 2 - х
х2 + х – 2 > 0.
Таким чином, множина розв' язків нерівності — це множина розв'язків системи
![]() 0 < х
0 < х ![]() 2
2
х2 + х – 2 > 0.
Розв'язуючи цю систему та ілюструючи проміжки існування її розв'язків, дістаємо: 1 < х ![]() 2.
2.
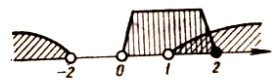
Приклад 12.
Розв'язати нерівність:
![]() .
.
Розв'язання.
Область визначення нерівності визначається за допомогою розв'язування системи нерівностей
![]()
![]() -х2 + 2х + 3
-х2 + 2х + 3 ![]() 0 х2 - 2х - 3
0 х2 - 2х - 3 ![]() 0,
0,
х2 + 1 ![]() 0 або х2 + 1
0 або х2 + 1 ![]() 0,
0,
х - 3 ![]() 0, х
0, х ![]() 3.
3.
Корені квадратного тричлена х2 - 2х - 3 дорівнюють х1 = 3, х2 = -1

Друга нерівність системи виконується при будь-яких значеннях х. Розв'язком даної системи нерівностей є х = 3. Підставивши це значення у вихідну нершність, дістанемо правильну числову тотожність: -2![]() < 0.
< 0.
Відповідь. х = 3.
Існує й загальний метод розв'язування нерівностей. Його обгрунтуванням є теорема, сформульована на попередньому занятті.
Розв'яжемо нерівність f (х) < > 0, де f (х) — довільна функція.
1. Знаходимо область визначення функції f (х).
2. Визначаємо всі її корені, тобто розв'язуємо рівняння f (х) = 0.
3. Розбиваємо за допомогою знайдених коренів область визначення функції f (х) на проміжки знакосталості.
4. Визначаємо, який знак має функція f (х) на кожному проміжку знакосталості. Отже, знаходимо множину значень аргументу х, при яких функція f (х) набуває додатних значень, тобто розв'язуємо нерівність f (х) > 0. Аналогічно розв'язуємо нерівність f (х) < 0.
Цей спосіб можна використовувати для розв'язування будь-яких нерівностей f (x) < > 0, якщо можна знайти область визначення функції f (х), а також її корені.
Приклад 13.
Розв'язати нерівність:
![]() .
.
Розв' язання.
Запишемо нерівність у вигляді
![]() .
.
1. Розглянемо функцію f(x) =![]() і знайдемо її область визначенняі 15 – х > 0, х < 15.
і знайдемо її область визначенняі 15 – х > 0, х < 15.
2. Знаходимо корені функції f(х):
![]() = 0.
= 0.
Дана нерівність рівносильна системі
![]() x < 15
x < 15
![]() = 3 - х, звідки
= 3 - х, звідки
![]() x < 15
x < 15
3 – х > 0
(![]() )2 = (3 – х)2.
)2 = (3 – х)2.
Після перетворення; дістанемо
![]() x < 3
x < 3
х2 - 5х - 6 = 0, x = -1.
Отже, область визначення функції ділиться на два проміжки знакосталості.
![]()
3. Визначаємо знаки функції f (х) на кожному проміжку.
а) х < - 1; f (-10) =![]() , тобто f (х) > 0;
, тобто f (х) > 0;
б) - 1 < х < 15; f (0) =![]() , тобто f (х) < 0.
, тобто f (х) < 0.
Розв'язком вихідної нерівності будуть ті проміжки, де f(x) < 0.
Відповідь. – 1 < х < 15.
Нерівності, що містять змінну під знаком модуля.
Розв'язуючи за означенням модуля нерівності з невідомим під знаком абсолютної величини, маємо:
1. |f(x)| < a.
а) Якщо а ![]() 0, нерівність розв'язків не має;
0, нерівність розв'язків не має;
б) якщо а > 0, то дана нерівність еквівалентна нерівності - а < f(х) < а.
2. |f (х) | > а.
а) Якщо а < 0, то розв'язком нерівності буде область визначення функції f (х);
б) якщо а > 0, то нерівність рівносильна сукупності нерівностей f(x)> a, f(x) < -а.
Приклад 1.
Розв'язати нерівність
![]() .
.
Розв'язання.
Дана нерівність рівносильна нерівності - 1 ![]()
![]()
![]() 1 або системі нерівностей
1 або системі нерівностей
![]()
![]()
![]() 1
1
![]()
![]() -1, звідки
-1, звідки
![]()
![]()
![]() - 1
- 1![]() 0
0 ![]()
![]() + 1
+ 1![]() 0,
0, ![]() .
.
Дана система нерівностей рівносильна системі
![]() (x - 4) (х + 1) (х - 2) (х + 2)
(x - 4) (х + 1) (х - 2) (х + 2) ![]() 0,
0,
(x + 4) (x - 1)(х - 2) (х + 2) ![]() 0,
0,
x ![]()
![]() 2.
2.
Розв'язуємо утворену систему методом інтервалів.
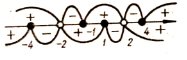
Відповідь. x ![]() 4, -1
4, -1 ![]() x
x ![]() 1, х
1, х ![]() -4.
-4.
Приклад 2.
Розв'язати нерівність
![]() ,
,
Розв'язання.
Дана нерівність рівносильна сукупності нерівностей
![]()
![]() 1, та
1, та ![]()
![]() -1,
-1,
або
![]()
![]() 0, та
0, та ![]()
![]() 0.
0.
![]()
![]() Ці нерівності рівносильні таким системам:
Ці нерівності рівносильні таким системам:
(x + 3)(x — 5) ![]() 0, (х - 1)(х - 5)
0, (х - 1)(х - 5) ![]() 0,
0,
х ![]() 5, та х
5, та х ![]() 5.
5.
Розв'язуємо нерівності методом інтервалів
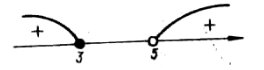
![]()
Відповідь. х ![]() -3, -1
-3, -1 ![]() х < 5, х > 5
х < 5, х > 5
Приклад 3.
Розв'язати нерівність
![]()
![]() 2.
2.
Розв'язання.
![]()
![]() Дана нерівність рівносильна сукупності систем:
Дана нерівність рівносильна сукупності систем:
![]()
![]() 2.
2.
х + 3 > 0
![]() х
х ![]() -2.
-2.
![]()
![]() 2.
2.
х + 3<0
х ![]() -2.
-2.
Розв'язуємо ці сукупності нерівностей:
![]()
![]()
![]()
![]()
![]() 2.
2. ![]()
![]() 2.
2.
х > -3 х < -3
х ![]() -2. х
-2. х ![]() -2.
-2.
![]()
![]()
![]() - 2
- 2 ![]() 0
0 ![]()
![]() - 2
- 2
х ![]() -2 х
-2 х ![]() -2
-2
х > -3 х < -3
![]()
![]()
![]()
![]()
х ![]() -2 х
-2 х ![]() -2
-2
х > -3 х < -3
-2 < x ![]() -
-![]() Розв'язків немає.
Розв'язків немає.
Розв'язуємо цю сукупність нерівностей методом інтервалів
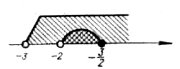
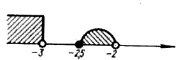
Відповідь. -2 < x ![]() -
-![]()
Нерівності з параметрами.
Багато понять і фактів, що відносяться до рівнянь, можна застосувати і до нерівностей.
Але логічна сторона розв'язання нерівностей більш змістовна в порівнянні з рівняннями.
Потрібно пам'ятати про те, що низка перетворень, придатних до рівнянь, у застосуванні до нерівностей має свої особливості. Якщо під час розв'язування рівнянь іноді розширюється ОДЗ або з'являються сторонні корені, які можна «відкинути» за допомогою перевірки, то під час розв'язування нерівності можна не тільки отримати або втратити розв'язки, але й дістати принципово неправильну відповідь.
Тому під час розв'язування нерівностей, особливо з параметрами, потрібно користуватися тільки рівносильними перетвореннями.
Нагадаємо, що дві нерівності
f(a,b,c,...,k,x) > g(a,b,c,...,k,x) і F(a,b,c,...,k,x) > G(a,b,c,...,k,x)
називаються рівносильними, якщо вони мають однакові спільні розв'язки при тій самій множині допустимих значень параметрів.
Наприклад, нерівності а2x-3 < ах+4 і ах < а7 рівносильні, тому що при а > 1 розв'язком кожної з них є (-![]() ; 7); при а = 1 — жодна з них розв'язків не має; при 0 < а < 1 розв'язки кожної з нерівностей: (7; +
; 7); при а = 1 — жодна з них розв'язків не має; при 0 < а < 1 розв'язки кожної з нерівностей: (7; +![]() ) і, нарешті, при а< 0 жодна з нерівностей не має змісту. Нерівності
) і, нарешті, при а< 0 жодна з нерівностей не має змісту. Нерівності
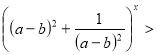
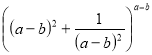 і
і ![]() >
> ![]()
нерівносильні, незважаючи на те, що як у першій, так і в другій множина розв'язків та ж сама: х є (а - b; +![]() ).
).
Але перша нерівність має зміст при будь-яких значеннях параметрів а і b, що задовольняють умову a ![]() b, а друга лише при а > b.
b, а друга лише при а > b.
Лінійні нерівності з однією змінною
Приклад 1
Розв'язати нерівність
(а - 1) х < 5а.
Розв'язання
При а=1 маємо 0<5, що виконується при будь-якому дійсному значенні х
При а > 1 х < ![]()
При а < 1 х > ![]()
Відповідь. х Є R при а = 1;
х Є ![]() при а >1
при а >1
х Є ![]() при а < 1
при а < 1
Приклад 2
Розв'язати нерівність
![]() .
.
Розв'язання
Зрозуміло, що а ![]() 2, х
2, х ![]() -3.
-3.
Початкову нерівність можна звести до такої:
![]() або
або  ,
,
яка рівносильна сукупності двох систем нерівностей:
![]()
![]() x >
x > ![]() або x <
або x < ![]() ,
,
x > -3 x < -3.
Порівняємо величини ![]() і – 3.
і – 3.
Для цього розглянемо їхню різницю:
![]() -( - 3) = -
-( - 3) = - ![]() =
= ![]()
![]()
При а < 0 і а > 2, ![]() < 0, тобто
< 0, тобто ![]() < -3,
< -3,
при 0 < а < 2 різниця ![]() додатна, тобто
додатна, тобто ![]() > -3.
> -3.
при а = 0 ![]() -(-3) = 0.
-(-3) = 0.
Таким чином, дістанемо, відповідь.
Відповідь. х Є ![]()
![]() (-3; +
(-3; +![]() ) при а Є (-
) при а Є (-![]() ; 0)
; 0) ![]() (2; +
(2; + ![]() );
);
х Є (-![]() ; -3)
; -3) ![]()
![]() при а Є [0; 2);
при а Є [0; 2);
розв'язків немає при а = 2.
Приклад 3
Розв'язати нерівність
(а2 - 4)х > а + 2.
Розв'язання
(а - 2)(а + 2)х > а + 2.
1. При а = -2 дістаємо 0х > 0, тобто х Є R.
2. При а = 2 0х ![]() 4 розв'язків нерівність не має.
4 розв'язків нерівність не має.
3. При а2 > 4 х ![]() .
.
4. При а2 < 4 х ![]()
![]()
Відповідь, х є R, якщо а = -2;
розв'язків немає, якщо а = 2;
х Є [![]() ; +
; + ![]() ), якщо а Є (-
), якщо а Є (-![]() ; -2)
; -2) ![]() (2; +
(2; +![]() );
);
х Є (-![]() ;
; ![]() ), якщо а Є (-2; 2)
), якщо а Є (-2; 2)
Приклад 4
Знайти розв'язки нерівності |х - a|(5х2 - 2х - 3) < 0 залежно від значення параметра а.
Розв 'язання
![]() x
x ![]() а,
а,
5 (x – 1)(x + ![]() ) < 0;
) < 0;
![]() -
- ![]() < х < 1,
< х < 1,
x ![]() а.
а.
Відповідь х Є (-![]() ; 1) при а Є (-
; 1) при а Є (-![]() ; -
; - ![]() ]
] ![]() [1; +
[1; + ![]() );
);
х Є (-![]() ; a)
; a) ![]() (a; 1) при а Є (-
(a; 1) при а Є (- ![]() ; 1).
; 1).
Приклад 5
Знайти розв'язки нерівності (х - а)|х2 - 4х + 3| > 0 залежно від значення параметра а.
![]()
![]() Розв'язання
Розв'язання
x – а > 0, x > а,
x ![]() 3, x
3, x ![]() 1,
1,
x ![]() 1; x
1; x ![]() 3;
3;
1) а < 1
![]()
х є (а; 1) ![]() (1; 3)
(1; 3) ![]() (3; +
(3; +![]() );
);
2) 1 ![]() а
а ![]() 3
3
![]()
х є (а; 3) ![]() (3; +
(3; +![]() );
);
3) а ![]() 3
3

х є (а; +![]() ).
).
Відповідь, х є (а; 1) ![]() (1; 3)
(1; 3) ![]() (3; +
(3; +![]() ), якщо х Є (-
), якщо х Є (-![]() ; 1];
; 1];
х є (а; 3) ![]() (3; +
(3; +![]() ); якщо х Є [1; 3);
); якщо х Є [1; 3);
х є (а; +![]() ), якщо х Є [3; +
), якщо х Є [3; +![]() ).
).
Приклад 6
Розв'язати нерівність
(1 - а) |х| < а2 - 1
Розв'язання
1. Якщо 1 – а > 0, тоді |х| < ![]() = - (а + 1). Здобута нерівність буде мати розв'язки, якщо - (а + 1) > 0.
= - (а + 1). Здобута нерівність буде мати розв'язки, якщо - (а + 1) > 0.
Розв'яжемо систему нерівностей:
![]() 1 – а > 0,
1 – а > 0,
- (а + 1) > 0.
![]() а < 1,
а < 1,
а < -1;
а є (-![]() ; -1).
; -1).
Отже, при а є (-![]() ; -1) нерівність має розв'язки: х Є (а+1; -(а+1)).
; -1) нерівність має розв'язки: х Є (а+1; -(а+1)).
2. При а = 1 вихідна нерівність набуває вигляду 0 . х < 0 — розв'язків немає.
3. Якщо 1 – а < 0, тоді |х| > ![]() = -(а+1).
= -(а+1).
Оскільки a>1 маємо: -(а + 1)< 0, здобута нерівність виконується при хЄR.
Відповідь. При a > 1 х є R;
при а є [-1; 1] розв'язків немає;
х Є (а+1; -(а+1)) при а < -1.
Квадратичні нерівності
Приклад 1
Розв'язати нерівність
ах2 - 2(а - 1)х + (а + 2) < 0.
Розв'язання
1. При а = 0 маємо 2х + 2 < 0, тобто х < -1.
2. При а ![]() 0 знайдемо дискримінант квадратного тричлена
0 знайдемо дискримінант квадратного тричлена
ах2 - 2(а - 1)х + (а + 2),
що міститься в лівій частині розглянутої нерівності.
D1 = ![]() = (а - 1)2 - а(а + 2) = 1 - 4а.
= (а - 1)2 - а(а + 2) = 1 - 4а.
Якщо D1 < 0, тобто при а > ![]() нерівність не має розв'язків.
нерівність не має розв'язків.
При а = ![]()
![]() х2 – 2 (-
х2 – 2 (-![]() )х + 2
)х + 2![]() < 0,
< 0,
х2 + 6х + 9 < 0,
(х + 3)2 < 0,
розв'язків немає.
Якщо D1 > 0, тобто при а є (-![]() ; 0)
; 0) ![]() (0;
(0; ![]() ), розглянемо два випадки:
), розглянемо два випадки:
- а < 0. У цьому випадку графіком функції f(х) = ах2 - 2(а - 1)х + а + 2 є парабола з напрямленими вниз вітками і розв'язком нерівності f(х) < 0 буде об'єднання двох числових проміжків:
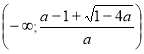 i
i  ;
;
 , тому що а < 0.
, тому що а < 0.
2) При 0 < а < ![]() розв'язком розглянутої нерівності буде числовий
розв'язком розглянутої нерівності буде числовий
проміжок  .
.
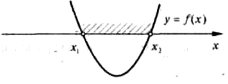
Тут 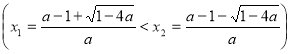 .
.
Відповідь, х Є 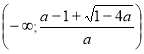
![]()
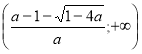 ; при а є (-
; при а є (-![]() ; 0);
; 0);
х Є 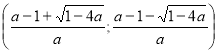 ; при а є (0;
; при а є (0; ![]() );
);
х Є (-![]() ;-1); при а = 0,
;-1); при а = 0,
розв'язків немає при а є [![]() ; +
; +![]() ).
).
Розглянемо приклад розв'язування нерівності з параметром і деякими додатковими умовами.
Приклад 2
Знайти всі значення а, при яких нерівність (х - 3а)(x – а - 3) < 0 виконується при всіх х, таких, що 1 < х < 3.
Розв'язання
Розв'язками заданої нерівності є один із проміжків (3а; а + 3) або (а + 3; 3а) (залежно від того, що більше: 3а або a + 3).
За умовою, відрізок [1; 3] повинен належати множині розв'язків. Отже, розв'язання нерівності зводиться до розв'язування наступної сукупності систем нерівностей:
![]() 3а < 1,
3а < 1,
a + 3 > 3 (1)
або
![]() а + 3 < 1,
а + 3 < 1,
3a > 3. (2)
З (1) маємо: 0 < а < ![]() .
.
Система (2) розв'язків не має.
Відповідь, a є (0; ![]() ).
).
Приклад 3
При яких значеннях параметра а нерівність
х2 - (3а - 4)х + (а - 1)(2a - 3) > 0
виконується при всіх додатних значеннях х?
Розв'язання
(х - (а - 1))(х - (2а - 3)) > 0.
Нерівність виконується при всіх додатних х, якщо обидва корені не-додатні, тобто
![]() a – 1
a – 1 ![]() 0,
0,
![]() 2а – 3
2а – 3 ![]() 0;
0;
a ![]() 1,
1,
а ![]() 1,5.
1,5.
Відповідь, а є (-![]() ; 1].
; 1].
Приклад 4
Знайти усі значення параметра а, при яких нерівність
(а - 3)х2 – (2а - 6)х + 2а – 7 ![]() 0
0
виконується при всіх дійсних значеннях х.
Розв'язання
1. Якщо а = 3, то дістанемо -1 ![]() 0, тобто х Є R.
0, тобто х Є R.
2. Якщо а ![]() 3, то нерівність виконана при всіх додатних х за умови:
3, то нерівність виконана при всіх додатних х за умови:
![]() а – 3 < 0,
а – 3 < 0,
D1 ![]() 0;
0;
![]() a < 3,
a < 3,
(a - 3)2 - (a - 3)(2a - 7) ![]() 0;
0;
![]() a < 3,
a < 3,
(a - 3)(4 - a) ![]() 0.
0.
![]() Таким чином, маємо:
Таким чином, маємо:
![]() a < 3,
a < 3,
4 – a ![]() 0,
0,
a = 3.
Відповідь, а є (-![]() ; 3].
; 3].
Приклад 5 .
Знайти розв'язок нерівності |х – 1| (х2 - (а + 3)х + 3а) < 0 залежно від значення параметра а.
Розв'язання
![]() x
x ![]() 1,
1,
(x – 3)(x – a) < 0.
1) а < 1
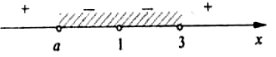
х Є (а; 1) ![]() (1; 3)
(1; 3)
2) 1 ![]() а
а ![]() 3,
3,
![]()
1 а 3
х Є (а; 3)
3) a = 3,
![]() x
x ![]() 1,
1,
(x – 3)2 < 0.
Система розв'язків не має.
4) а > 3
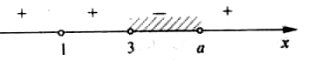
х Є (3; а)
Відповідь, х Є (а; 1) ![]() (1; 3), якщо а є (-
(1; 3), якщо а є (-![]() ; 1);
; 1);
х Є (а; 3), якщо а є [1; 3);
розв'язків не має якщо х = 3;
х Є (3; а), якщо а є (3; +![]() ).
).
Приклад 6
Знайти всі значення а, при яких розв'язками нерівності
(х - а)2(х - 2)(х + 3) < 0
є відрізок.
Розв'язання
![]() Вочевидь, що дана нерівність рівносильна сукупності
Вочевидь, що дана нерівність рівносильна сукупності
(х - 2)(х + 3) < 0,
х = а.
Оскільки розв'язками першої нерівності сукупності є відрізок [-3; 2], то для виконання умови завдання необхідно, щоб а є [-3; 2].
Відповідь. При а є [-3; 2].
Приклад 7
Знайти всі значення параметра а, при яких нерівність
![]()
виконується при всіх значеннях змінної х.
Розв'язання
Оскільки х2 - 14х + 53 > 0 при всіх дійсних значеннях змінної х, то достатньо з'ясувати, при яких значеннях параметра а виконується нерівність
(a - 1)х2 + 2(3 - 2а)х + 12а – 14 < 0
для будь-яких х.
![]() Нерівність (a - 1)х2 + 2(3 - 2а)х + 12а – 14 < 0 виконується при всіх значеннях змінної тоді й тільки тоді, коли
Нерівність (a - 1)х2 + 2(3 - 2а)х + 12а – 14 < 0 виконується при всіх значеннях змінної тоді й тільки тоді, коли
a – 1 < 0,
![]() (3 – 2a)2 - (а - 1)(12а - 14) < 0;
(3 – 2a)2 - (а - 1)(12а - 14) < 0;
![]() a < 1, а < 1,
a < 1, а < 1,
![]() -8а2 + 14а - 5 < 0; 8а2 - 14а + 5 > 0;
-8а2 + 14а - 5 < 0; 8а2 - 14а + 5 > 0;
а<1,
![]() a >
a > ![]() ,
,
a < ![]() .
.
Звідки маємо: а є (-![]() ;
;![]() ) .
) .
Відповідь, а є (-![]() ;
;![]() ) .
) .
Доведення нерівностей.
При доведенні нерівностей часто припускають логічну помилку. Вона полягає в тому, що, застосовуючи різні перетворення і діставши очевидну нерівність (наприклад, (а - b)2 ![]() 0), роблять висновок: «з цього випливає, що нерівність доведена». Тобто ми довели, що коли припустити, що вихідна нерівність правильна, то отримана в результаті перетворень нерівність теж правильна. Адже правильність отриманої нерівності очевидна, а про вихідну нерівність, яку треба було довести, ми так нічого й не знаємо.
0), роблять висновок: «з цього випливає, що нерівність доведена». Тобто ми довели, що коли припустити, що вихідна нерівність правильна, то отримана в результаті перетворень нерівність теж правильна. Адже правильність отриманої нерівності очевидна, а про вихідну нерівність, яку треба було довести, ми так нічого й не знаємо.
Правильно було б проводити міркування в оберненому порядку. Треба взяти деяку очевидно правильну нерівність і провести такі перетворення, що приводять до нерівності, яку треба довести. З'ясуємо, як це зробити. Будемо розглядати вище розглядуване перетворення вихідної нерівності як пошук можливого доведення. Якщо в результаті такого пошуку вдалося прийти до очевидно правильної нерівності, то можна починати справжнє доведення. Від цієї очевидної нерівності за допомогою тих самих перетворень, тільки в оберненому порядку, перейти до вихідної нерівності.
Але якщо при зведенні даної нерівності до очевидної кожного разу заміняти нерівність на рівносильну їй, перевіряючи і підкреслюючи це, то обернені перетворення не потрібні.
Приклад 1.
Довести, що при а > 0 справджується нерівність
a + ![]()
![]() 4.
4.
Доведення.
1-й спосіб. (Пряме доведення.)
Для будь-якого дійсного числа а, квадрат різниці а - 2 є невід'ємним числом, тобто (а - 2)2 > 0 — правильна нерівність. Розкривши дужки в лівій частині цієї нерівності, дістанемо правильну нерівність: а2 - 4а + 4 ![]() 0.
0.
Оскільки за умовою а > 0, то, поділивши всі члени останньої нерівності на а, дістанемо також правильну нерівність:
a – 4 + ![]()
![]() 0.
0.
Додамо до обох частин цієї нерівності число 4, дістанемо правильну нерівність: a + ![]()
![]() 4. Що й треба було довести.
4. Що й треба було довести.
Нерівність доведено
2-й спосіб. (Обернене доведення.)
Припустимо, що та нерівність, яку тріеба довести, правильна, тобто
a + ![]()
![]() 4 при а > 0. (*)
4 при а > 0. (*)
Тоді, помноживши всі члени цієї нерівності на а > 0, дістанемо рівносильну нерівність:
а2 + 4 > 4а. (**)
Нерівність (**) рівносильна такій нерівності:
а2+ 4 - 4а ![]() 0. (***)
0. (***)
А остання нерівність у свою чергу рівносильна нерівності:
(а - 2)2 ![]() 0. (****)
0. (****)
Нерівність (****) правильна, оскільки квадрат будь-якого дійсного числа є числом невід'ємним. Тоді правильна й вихідна нерівність (*), оскільки вона рівносильна нерівності (****).
3-й спосіб. (Доведення від супротивного).
Доведення від супротивного грунтується на такому логічному законі: якщо з висловлення А випливає висловлення В і висловлення В — хибне, то хибне також і висловлення А.
Отже, повернемося до розглядуваної нерівності. Протилежною до нерівності a + ![]()
![]() 4 є нерівність
4 є нерівність
a + ![]() < 4 (*),
< 4 (*),
Припустимо, що нерівність (*) правильна. Помноживши обидві частини цієї нерівності на а > 0, дістанемо рівносильну нерівність а2 + 4 < 4а, з якої випливає, що
а2 + 4 - 4а < 0, або (а - 2)2 < 0. (**)
Нерівність (**) є наслідком нерівності (*), але вона хибна, оскільки квадрат дійсного числа а - 2 не може бути від'ємним числом. Отже, хибна й нерівність (*). Тому правильна протилежна до неї нерівність, а саме
а + ![]() > 4, що й треба було довести.
> 4, що й треба було довести.
Приклад 2.
Довести, що для будь-яких дійсних х і у
х2 + 5у2 - 4ху + 2х - 6у + 3 > 0.
Розв'язання.
Розглянемо ліву частину нерівності як квадратний тричлен щодо х:
А = х2 + 2х (1 - 2у) + (5у2— 6у + 3).
Знайдемо дискримінант цього тричлена.
D = (2 (1 - 2у)2 - 4 (5у2 - 6у + 3) = 4 (-у2 + 2у - 2) = -4 ((у - 1)2 + 1)< 0.
Оскільки дискримінант квадратного тричлена від'ємний для будь-яких у, то знак квадратного тричлена збігається зі знаком коефіцієнта при х2, тобто він додатний для всіх х та у, що й треба було довести.
Приклад 3.
Довести, що при будь-якому додатному а справджується нерівність
![]() +
+ ![]() < 2
< 2![]()
Розв'язання.
Запишемо дану нерівність у вигляді
![]() -
- ![]() <
< ![]() -
- ![]()
Перенесемо ірраціональність із чисельника в знаменник. Маємо:
![]()
Здобута нерівність правильна при будь-яких додатних значеннях а. Вона утворилася з попередніх шляхом рівносильних перетворень, тобто правильна й нерівність, яку треба було довести.
Приклад 4.
Довести, що в будь-якому трикутнику подвоєна сума всіх медіан більша, ніж сума всіх його сторін.
Розв' язання.
Позначимо сторони трикутника через а, b, с, а відповідні їм медіани mа, тb, тс. Розглянемо трикутник, основою якого є сторона с, а вершина міститься в точці перетину медіан. За властивостями сторін трикутника маємо:
![]() ma +
ma + ![]() mb > c
mb > c
aбо
2ma + 2 mb > 3c,
2тb + 2тс > 3а,
2та + 2тс >3b .
Додавши утворені нерівності, дістанемо:
4ma + 4 mb + 4тс > 3(a + b + c),
2(та + тb + тс) > ![]() (a + b + c).
(a + b + c).
Посилюючи утворену нерівність, матимемо:
2 (та + тb + тс) > а + b + с,
що й треба було довести.
Приклад 5.
Довести, що для будь-яких значень х справджується нерівність
х18 - х17+ х6 - х + 1 > 0.
Розв'язання.
Визначимо знак лівої частини нерівності на кожному з проміжків х ![]() 0, 0 < x < 1, х
0, 0 < x < 1, х ![]() 1.
1.
1. Якщо х ![]() 0, то всі парні степені х невід'ємні, а - х17 та -х набувають також невід'ємних значень. Отже, ліва частина даної нерівності на цьому проміжку набуває додатних значень і нерівність справджується.
0, то всі парні степені х невід'ємні, а - х17 та -х набувають також невід'ємних значень. Отже, ліва частина даної нерівності на цьому проміжку набуває додатних значень і нерівність справджується.
2. Якщо 0 < х < 1, то, перетворюючи ліву частину нерівності х18 - х17+ + х6 - х + 1 = х8 + х6(1 – x11) + (1 - х), переконуємося, що на цьому проміжку ліва частина нерівності також набуває додатних значень. Отже, дана нерівність на проміжку (0; 1) справджується.
3. Якщо х ![]() 1, то, перетворюючи ліву частину нерівності х18 - х17+ + х6 - - х + 1 = x17(x - 1) + x (x5 - 1) + 1 переконуємося, що, оскільки вирази у дужках набувають невід'ємних значень, то на цьому проміжку дана нерівність також справджується.
1, то, перетворюючи ліву частину нерівності х18 - х17+ + х6 - - х + 1 = x17(x - 1) + x (x5 - 1) + 1 переконуємося, що, оскільки вирази у дужках набувають невід'ємних значень, то на цьому проміжку дана нерівність також справджується.
Отже, на кожному з розглянутих проміжків дана нерівність справджується, тобто вона справджується при будь-якому значенні х. Що й треба було довести.
Класичні нерівності.
Приклад 1.
Довести, що для а > 0 і b > 0 має місце нерівність
4(а3 + b3) ![]() (a + b)3.
(a + b)3.
Розв'язання
Розглянемо вираз 4(а3 + b3) -(a + b)3, , що є різницею лівої та правої частин даної в умові нерівності, і виконаємо його перетворення:
4(а3 + b3) - (а + b)3 = 4а3 + 4b3 - а3 - 3а2b - 3аb2 – b3 = 3а3 + 3b3 - 3а2b - 3аb2 = =3((a3 - a2b) + (b3 - b2a))=3(a2(a - b) - b2(a - b))= 3(a - b)(a2 - b2)= 3(a - b)2(a + b).
Оцінимо знак отриманого виразу.
(а - b)2 ![]() 0 для довільних а і b, а + b > 0 , оскільки а > 0 і b > 0 .
0 для довільних а і b, а + b > 0 , оскільки а > 0 і b > 0 .
Отже,
3(а - b)2(а + b) > 0,
тому
4(а3 + b3) - (а + b)3 ![]() 0,
0,
звідки
4(а3 + b2) ![]() (а + b)3
(а + b)3
Приклад 2.
Довести, що для будь-якого n є N справедлива нерівність
![]() +
+ ![]() +
+ ![]() + … +
+ … + ![]() < 2.
< 2.
Розв'язання
Оскільки для п є N і n ![]() 2 виконується умова
2 виконується умова
![]() <
< ![]() ,
,
то маємо:
![]() <
< ![]() ,
,
![]() <
< ![]() ,
,
. . . . . . . . .
![]() <
< ![]() ,
,
Тоді
![]() +
+ ![]() +
+ ![]() + … +
+ … + ![]()
![]() 1 +
1 + ![]() +
+ ![]() + . . . +
+ . . . + ![]() .
.
Використаємо рівність
![]() де к є N,
де к є N,
справедливість якої легко перевірити, виконавши такі перетворення:
![]() .
.
Тоді
1 + ![]() +
+ ![]() + . . . +
+ . . . + ![]() = 1+ (1 -
= 1+ (1 - ![]() ) + (
) + (![]() -
- ![]() ) + . . . + (
) + . . . + (![]() -
- ![]() ) = 1 -
) = 1 - ![]() .
.
Оскільки 2 - ![]() < 2 для будь-якого п є N , то це і доводить дану в умові нерівність.
< 2 для будь-якого п є N , то це і доводить дану в умові нерівність.
Приклад 3.
(Нерівність, що пов'язує середнє геометричне та середнє арифметичне двох чисел.) Довести, що для будь-яких а ![]() 0 , b
0 , b ![]() 0 виконується нерівність
0 виконується нерівність
![]() (1)
(1)
Рівність досягається тоді і тільки тоді, коли а = b .
Доведення
Для а ![]() 0 і b
0 і b ![]() 0 виконується нерівність
0 виконується нерівність
(![]() )2
)2 ![]() 0.
0.
Отже,
a - 2![]() + b
+ b ![]() 0,
0,
звідки
![]() .
.
Якщо
![]() , то (
, то (![]() )2 = 0 і а = b
)2 = 0 і а = b
Якщо а = b , то ![]() i
i ![]()
Тоді ![]()
Розглянемо приклади використання нерівності (1) для доведення інших нерівностей.
Приклад 4.
Довести, що для довільною а > 0 справедлива нерівність
![]() .
.
Розв'язання
За нерівністю (1) маємо:
![]()
![]()
![]() ,
,
![]()
![]() 1,
1,
![]()
![]() 2.
2.
Рівність досягається лише для а = 1.
Приклад 5.
Довести, що для а > 0 і b > 0 має місце нерівність
(a + b)(![]() )
) ![]() 4,
4,
Розв'язання
За нерівністю (1) маємо:
![]()
![]()
![]() ,
,
звідки
а + b ![]() 2
2![]() .
.
Аналогічно
![]()
![]() 2
2![]() ,
,
тому
(a + b)(![]() )
) ![]()
![]() ,
,
(a + b)(![]() )
) ![]() 4.
4.
Приклад 6.
Довести, що для а > 0, b > 0 і с > 0 справджується нерівність
(1 + ![]() )(1 +
)(1 + ![]() )(1 +
)(1 + ![]() )
) ![]() 8.
8.
Розв'язання
За нерівністю (1) маємо:
1 + ![]()
![]() 2
2![]() ,
,
1 + ![]()
![]() 2
2![]() ,
,
Аналогічно
1 + ![]()
![]()
![]() ,
,
1 + ![]()
![]()
![]() ,
,
Тому
(1 + ![]() )(1 +
)(1 + ![]() )(1 +
)(1 + ![]() )
) ![]()
![]() ,
,
(1 + ![]() )(1 +
)(1 + ![]() )(1 +
)(1 + ![]() )
) ![]() 8.
8.
Приклад 7.
Довести справедливість нерівності
![]()
для а > 0 , b > 0 , с > 0.
Розв'язання
За нерівністю (1) маємо:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тоді
(![]() ) + (
) + (![]() ) + (
) + (![]()
![]() 2a + 2b + 2с.
2a + 2b + 2с.
звідки
![]()
Приклад 8
Довести справедливість нерівності
![]()
для а ![]() 0, b
0, b ![]() 0 і с
0 і с ![]() 0.
0.
Розв'язання
 .
.
Позначимо
![]() = d.
= d.
Тоді
d = ![]() .
.
За нерівністю (1) маємо:
![]() ,
,
![]() .
.
З останніх двох нерівностей маємо:
![]() +
+![]()
![]() 2
2![]() .
.
Тоді
![]()
![]() 2
2![]() ,
,
![]()
![]()
![]() ,
,
d ![]()
![]() , d4
, d4 ![]() abcd,
abcd,
звідки
d3 ![]() abc, тобто
abc, тобто
![]() .
.
Приклад 9.
Довести справедливість нерівності
(а + b + с)![]()
![]() 9
9
для а > 0, b > 0, с > 0.
Розв'язання
Використовуючи нерівність, доведену в прикладі 8, отримаємо:
а + b + с ![]() 3
3![]() ,
,
![]()
![]() 3
3 ![]() ,
,
(а + b + с)![]()
![]() 9
9
Приклад 10.
Довести, що для b ![]() 0 виконується нерівність
0 виконується нерівність
![]()
![]() 3a2 b3 – 16.
3a2 b3 – 16.
Розв'язання
Доведемо, що
a6 + b9+ 64 ![]() 12a2b3.
12a2b3.
Для цього використаємо нерівність, доведену в прикладі 8, для чисел а6, b9 та 64.
Маємо:
![]() .
.
Оскільки ![]() = 4a2b3, то
= 4a2b3, то
а6 + b9 + 64 ![]() 12a2b3,
12a2b3,
![]()
![]() 3a2 b3 – 16.
3a2 b3 – 16.
Приклад 11.
Довести, що для а > 0 і b > 0 мають місце такі нерівності:
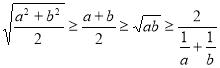 , (2)
, (2)
де ![]() - середнє арифметичне а і b,
- середнє арифметичне а і b,
![]() — середнє геометричне а і b,
— середнє геометричне а і b,
![]() - середнє квадратичне а і b,
- середнє квадратичне а і b,
![]() — середнє гармонійне а і b.
— середнє гармонійне а і b.
Доведення
Нерівність для середнього арифметичного і середнього геометричного вже доведено.
Доведемо дві інші нерівності:
![]()
та
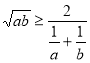
Оскільки (а - b)2 ![]() 0 , то а2 - 2ab + b2
0 , то а2 - 2ab + b2 ![]() 0 , 2a2 + 2b2
0 , 2a2 + 2b2 ![]() a2 + 2ab + b2,
a2 + 2ab + b2,
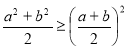 ,
,
![]()
Аналогічно
![]() ,
,
звідки
a - 2![]() + b
+ b ![]() 0 ,
0 ,
a + b ![]() 2
2![]() ,
,
1 ![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
Приклад 12.
Довести, що для а > 0, b > 0 і с > 0 має місце нерівність
a4 +b4 +c4 ![]() abc(a + b + c).
abc(a + b + c).
Розв'язання
Перетворимо праву частину нерівності:
abc(a + b + с) = а2bс + ab2с + abc2.
За нерівністю (2) маємо:
![]() ,
,
![]() ,
,
![]() .
.
Отже,
![]() ,
,
![]() ,
,
![]() .
.
Тому
a2bc + ab2c + abc2 ![]()
![]() = b2a2 + 2a2c2 + 2c2b2
= b2a2 + 2a2c2 + 2c2b2 ![]()
![]() + +
+ +![]() +
+ ![]() = a4 + b4 + c4.
= a4 + b4 + c4.
Отже,
a4 + b4 + c4 ![]() abc(a + b + c).
abc(a + b + c).
4. Системи рівнянь і нерівностей
Детермінанти (визначники), їх обчислення. Системи лінійних рівнянь з трьома невідомими. Правило Крамера
Нехай маємо числа а11, а12, а21, a22. Таблиця, яка має вигляд (1)
 , (1)
, (1)
зветься матрицею другого порядку, числа а11, а12, а21, a22 — її елементами, причому перший індекс у записі числа вказує на номер рядка, в якому стоїть цей елемент, а другий — на номер стовпця.
Число ![]() = а11а22 — а12а21 називається визначником матриці (1) або визначником другого порядку і позначається
= а11а22 — а12а21 називається визначником матриці (1) або визначником другого порядку і позначається
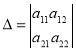 .
.
Цілком аналогічно, розглядаючи таблицю вигляду
 ,
,
де аij (і = 1, 2, 3; j = 1, 2, 3) — деякі числа, маємо матрицю третього порядку, визначник якої позначається
 . (2)
. (2)
У цьому випадку число ![]() знаходять за формулою
знаходять за формулою
![]() = а11а22a33 + а12а23a31 + а13а21a32 - а13а22a31 - а11а23a32 - а12а21a33 (3)
= а11а22a33 + а12а23a31 + а13а21a32 - а13а22a31 - а11а23a32 - а12а21a33 (3)
Визначник третього порядку можна виразити через визначники другого порядку:
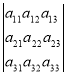 = a11
= a11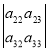 - a12
- a12![]() - a13
- a13![]() (4)
(4)
Основні властивості визначника
1. Величина визначника не зміниться, якщо рядки та стовпці його поміняти місцями, тобто
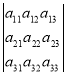 =
= 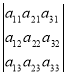 .
.
2. Якщо у визначнику поміняти місцями лише два рядки або два стовпці, то знак визначника змінюється на протилежний.
3. Якщо всі елементи деякого рядка (стовпця) помножити на те саме число, то значення визначника також помножиться на те саме число. Звідси зрозуміло, що спільний множник всіх елементів рядка (стовпця) можна виносити за знак визначника.
4. Якщо визначник містить два пропорційних рядки (стовпці), то значення його дорівнює нулю. Отже, якщо елементи деякого рядка (стовпця) дорівнюють нулю, то і сам визначник дорівнює нулю.
5. Величина визначника не змінюється, якщо до елементів одного рядка (стовпця) додати елементи другого рядка (стовпця), помножені на те саме число.
Нехай дано систему лінійних рівнянь
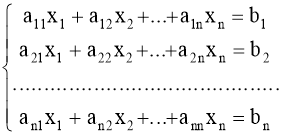 (1)
(1)
Коефіцієнти a11, а12, ... , a1n ..., an1, b2 ..., bn вважаються заданими .
Вектор - рядок x1, x2, ..., xn - називається розв’язком системи (1), якщо при підстановці цих чисел замість змінних всі рівняння системи (1) перетворюються у правильну рівність.
Визначник n-го порядку а ij , складений з коефіцієнтів при змінній, називається визначником системи (1). Залежно від визначника системи (1) розрізняють наступні випадки.
a). Якщо , то система (1) має єдиний розв’язок, яке може бути знайдений за формулами Крамера : x1=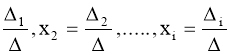 , де
, де
визначник n-го порядку i ( i = 1,2...,n) виходить з визначника системи шляхом заміни i-го стовпця вільними членами b1, b2..., bn.
б). Якщо , то система (1) або має нескінченну множину розв’язків, або несумісна, т.е. розв’язків немає.
Наприклад розглянемо систему 3-х лінійних рівнянь з трьома невідомими.
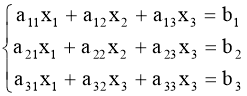 (2).
(2).
1. В даній системі складемо визначник 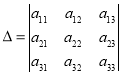 і обчислимо.
і обчислимо.
2. Скласти і обчислити наступні визначники :
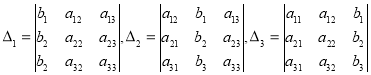 .
.
3. Скористатися формулами Крамера.
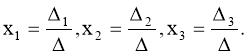
Приклад 1.
Розв’язати систему лінійних рівнянь.
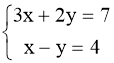 .
.
Розв’язання
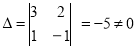
![]()
![]()
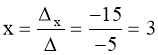
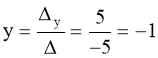 .
.
Перевірка:
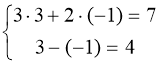
Відповідь: ( 3 ; -1 ).
Приклад 2.
Розв’язати систему лінійних рівнянь.

Розв’язання
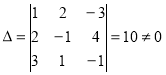

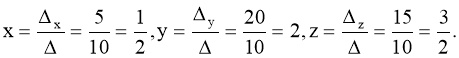
Перевірка:
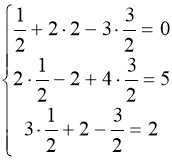
Відповідь: x = 0,5 ; y = 2 ; z = 1,5 .
Приклад 3.
Розв’язати систему лінійних рівнянь.
![]() 2х + 3у = 7,
2х + 3у = 7,
3х + 2у = 9.
Розв’язання
Маємо ![]() ,
,
![]() ,
,
![]() .
.
Відповідь: x = ![]() ; y =
; y = ![]() .
.
Приклад 4.
Розв’язати систему лінійних рівнянь.
![]() 2х + у + 3z = 9,
2х + у + 3z = 9,
x – 2y + z = -2,
3x + 2y + 2z = 7.
Розв’язання
Маємо
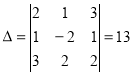 ,
,
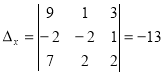 ,
, 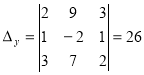 ,
, 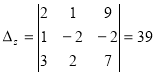 .
.
Відповідь: x = -1 ; y = 2 ; z = 3
Системи однорідних лінійних рівнянь. Розв'язування систем лінійних рівнянь методом Гаусса
Система двох однорідних лінійних рівнянь з трьома невідомими
![]() а11х1 + а12х2 + а13х3 = 0,
а11х1 + а12х2 + а13х3 = 0,
а21х1 + а22х2 + а23х3 = 0, (1)
має розв язки
х1 = k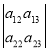 , х2 = -k
, х2 = -k![]() , х3 = k
, х3 = k![]() ,
,
де k — довільне число.
Система трьох однорідних лінійних рівнянь з трьома невідомими
![]() а11х1 + а12х2 + а13х3 = 0,
а11х1 + а12х2 + а13х3 = 0,
а21х1 + а22х2 + а23х3 = 0,
а31х1 + а32х2 + а33х3 = 0,
має ненульові розв'язки, якщо визначник системи
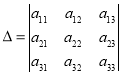 = 0
= 0
Справедливе і обернене твердження.
Крім формул Крамера при розв'язуванні систем п лінійних рівнянь з п невідомими використовують також метод Гаусса. Нехай маємо систему трьох лінійних рівнянь з трьома невідомими
![]() а11х1 + а12х2 + а13х3 = b1,
а11х1 + а12х2 + а13х3 = b1,
а21х1 + а22х2 + а23х3 = b2, (2)
а31х1 + а32х2 + а33х3 = b3.
Припустимо, що а11 ![]() 0. Поділимо обидві частини першого рівняння системи на а11 і, помноживши одержане рівняння спочатку на а21, а потім на а31, віднімемо відповідно від другого і третього рівнянь системи. Дістанемо
0. Поділимо обидві частини першого рівняння системи на а11 і, помноживши одержане рівняння спочатку на а21, а потім на а31, віднімемо відповідно від другого і третього рівнянь системи. Дістанемо
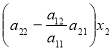 +
+ 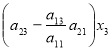 = b2 -
= b2 - ![]() ,
,
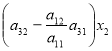 +
+ 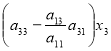 = b3 -
= b3 - ![]() .
.
Введемо позначення
![]() ,
, ![]() , b2 -
, b2 - ![]() =
= ![]() ,
,
![]() ,
, ![]() , b3 -
, b3 - ![]() =
= ![]() .
.
Дістанемо систему
![]()
![]()
![]() (3)
(3)
Нехай ![]() 0, тоді, поділивши обидві частини першого рівняння системи (3) на
0, тоді, поділивши обидві частини першого рівняння системи (3) на ![]() та віднявши одержане рівняння, помножене на
та віднявши одержане рівняння, помножене на ![]() , від другого рівняння системи (3), матимемо
, від другого рівняння системи (3), матимемо
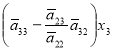 =
= ![]() .
.
Позначивши ![]() ,
, ![]() = b'3, дістанемо
= b'3, дістанемо
![]() = b'3
= b'3
У результаті зазначених операцій система рівнянь (2) набирає вигляду
![]() х1 +
х1 + ![]() х2 +
х2 + ![]() х3 =
х3 = ![]() ,
,
х2 + ![]() х3 =
х3 = ![]() , (4)
, (4)
х3 = ![]() .
.
Визначення невідомих, починаючи з останнього, зрозуміле. Якщо ж а11 = 0, то серед коефіцієнтів при х1 (а21 або а31) існує хоча б один відмінний від нуля. Рівняння, з коефіцієнтом відмінним від нуля при x1, вважатимемо першим.
Назвемо таблицю, що складена з коефіцієнтів при невідомих та вільних членів системи, розширеною матрицею системи. Ця матриця має вигляд
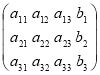
Приклад 1.
Методом Гаусса розв'язати систему рівнянь
![]() х1 + 2х2 + 3х3 = 5,
х1 + 2х2 + 3х3 = 5,
х1 + 3х2 + 4х3 = 6,
2х1 - х2 - х3 = 1.
Розв’язання
Помножимо спочатку перше рівняння системи на -1 і додамо до другого, а потім помножимо перше рівняння системи на -2 і додамо до третього рівняння. Дістанемо
![]() х1 + 2х2 + 3х3 = 5,
х1 + 2х2 + 3х3 = 5,
х2 + х3 = 1,
- 5х2 - 7х3 = -9.
Тепер помножимо друге рівняння на 5 і додамо до третього рівняння, матимемо
![]() х1 + 2х2 + 3х3 = 5,
х1 + 2х2 + 3х3 = 5,
х2 + х3 = 1,
- 2х3 = -4.
Зрозуміло, що х3 = 2. З другого рівняння знаходимо x2 = -1, тоді з першого рівняння x1 = 1.
Відповідь: x1 = 1, x2 = -1, х3 = 2.
Приклад 2.
Розв'язати систему однорідних лінійних рівнянь
![]() х1 + 2х2 + 3х3 = 0,
х1 + 2х2 + 3х3 = 0,
3х1 - 5х2 + 3х3 = 0,
2х1 + 7 х2 - 3х3 = 0.
Розв’язання
Оскільки визначник системи ![]() = 86
= 86 ![]() 0, то система має тільки нульові розв'язки.
0, то система має тільки нульові розв'язки.
Відповідь: x1 = x2 = х3 = 0.
Приклад 3.
Розв'язати систему однорідних лінійних рівнянь
![]() х1 + х2 + х3 = 0,
х1 + х2 + х3 = 0,
3х1 + 6х2 + 5х3 = 0,
х1 + 4 х2 + 3х3 = 0.
Розв’язання
Знайдемо визначник системи:
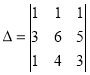 = 0
= 0
Отже, система має розв'язки, відмінні від нульових. Розглянемо систему перших двох рівнянь (третє є їх наслідком):
![]() х1 + х2 + х3 = 0,
х1 + х2 + х3 = 0,
3х1 + 6х2 + 5х3 = 0.
Розв'язуючи її, дістаємо х2 = 2х1, х3 = -3х1. Надаючи довільних значень х1, знайдемо відповідні значення х2 і х3. Тобто система рівнянь має безліч розв'язків.
Відповідь: система рівнянь має безліч розв'язків.
Перші уявлення про лінійне програмування.
Лінійне програмування - це наука про методи дослідження і знаходження найбільших і найменших значень лінійної функції, на невідомі якої накладені лінійні обмеження. Таким чином, задачі лінійного програмування відносяться до задач на умовний екстремум функції. Здавалося б, що для дослідження лінійної функції багатьох змінних на умовний екстремум достатньо застосувати добре розроблені методи математичного аналізу, проте неможливість їх використання можна досить просто проілюструвати.
Дійсно, нехай необхідно досліджувати на екстремум лінійну функцію
Z = С1х1 + С2х2 + ... + Сnxn
при лінійних обмеженнях
a11x1 + a12x2 + ... + a1nxn = b1
a21x1 + a22x2 + ... + a2nxn = b2
. . . . . . . . . . . . . . .
am1x1 + am2x2 + ... + amnxn = bm
Оскільки Z - лінійна функція, то = Сj (j = 1, 2 ..., n), то всі коефіцієнти лінійної функції не можуть бути рівнi нулю, отже, усередині області, утвореної системою обмежень, екстремальні точки не існують. Вони можуть бути на межі області, але досліджувати точки границі неможливо, оскільки часткові похідні є константами.
Для розв’язування задач лінійного програмування було потрібно створення спеціальних методів. Особливо широке розповсюдження лінійне програмування отримало в економіці, оскільки дослідження залежності між величинами, що зустрічаються в багатьох економічних задачах, приводить до лінійної функції з лінійними обмеженнями, накладеними на невідомі.
Системи симетричних рівнянь.
Вираз f (x, y) називається симетричним, якщо при заміні х на у, у на х він не змінюється.
Приклади симетричних виразів: f (x, y) = х + у; f (x, y) = х2 + у2; f (x, y) = х3 + у3; f (x, y) = ![]() + ху; f (x, y) = 2х2 + 5ху + 2у2.
+ ху; f (x, y) = 2х2 + 5ху + 2у2.
Вирази (х + у) і ху називаються основними симетричними многочленами з двома змінними. Усі симетричні вирази з двома змінними виражаються через основні симетричні многочлени. Наприклад:
х2 + ху + у2 = (х + у)2 - ху;
х2 + у2 = (х + у)2-2ху;
х3 + у3 = (х + у)(х2 - ху + у2) = (х + у)((х + у)2 - 3xy) = (x + y)3 - 3(х + у)ху.
Симетричною системою рівнянь називається система, усі рівняння якої симетричні. Розв'язувати симетричну систему можна, наприклад, за допомогою заміни змінних, де новими змінними є основні симетричні многочлени.
При розв'язуванні систем, симетричних відносно х і у, часто доцільно вводити нові допоміжні невідомі
![]()
![]()
![]() х + у = и або х2 + у2 = и або x - у = и
х + у = и або х2 + у2 = и або x - у = и
ху = v xy = v, xy = v
х3 + у3 = …= u3 – 3uv,
х4 + у4 = …= u4 – 3u2 v + 2v2,
х5 + у5 = …= u5 – 5u3 v + 5uv2,
x2 + xy + y2 = … = u2 - v
тощо.
Приклад 1.
Розвязати систему
![]() х2 + у2 = 34
х2 + у2 = 34
х + у + ху = 23.
Розв'язання.
Оскільки х2 + у2 = (х + у)2 - 2ху, то, поклавши х + у = и, xy = v, приходимо до такої системи:
![]() u2 – 2v = 34
u2 – 2v = 34
![]()
![]() u + v = 23. Із цієї системи знаходимо
u + v = 23. Із цієї системи знаходимо
и1 = 8 и2 = -10
v1 = 15; v2 = 33.
Звідси початкова система еквівалентна такій сукупності систем:
![]()
![]() x + y = 8 x + y = -10
x + y = 8 x + y = -10
ху =15; ху = 33.
Перша система сукупності має розв'язки (3; 5), (5; 3); друга система розв'язків не має.
Відповідь: (3; 5); (5; 3).
Приклад 2.
Розв'язати систему
![]() x4 + 6x2y2 + у4 = 136
x4 + 6x2y2 + у4 = 136
х3у + ху3 = 30.
Розв'язання.
x4 + 6x2y2 + у4 = (х2 + у2)2 + 4х2у2 = ((х + у)2 -2xy)2 + 4(ху)2,
х3у + ху3 = ху(х2 + у2) = ху ((х + у)2 - 2ху).
Зробимо заміну х + у = и, ху = v, тоді задана система зводиться до такої:
![]() (и2 – 2v)2 + 4v2 = 136 (а)
(и2 – 2v)2 + 4v2 = 136 (а)
v(u2 -2v) = 30. (б)
З рівняння (б) останньої системи и2 - 2v = ![]() ; підставляючи в (а), дістаємо:
; підставляючи в (а), дістаємо:
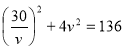
![]()
![]()
![]() 4v4 – 136v2 + 900 = 0
4v4 – 136v2 + 900 = 0 ![]() v4 – 34v2 + 225 = 0
v4 – 34v2 + 225 = 0
Розв'язуючи це біквадратне рівняння, знаходимо: v = ±5; v = ±3.
З (б) u2 – 2v = ![]()
![]() u2 = 2v +
u2 = 2v + ![]()
Підставляючи знайдені значення v, дістаємо:
v = 5 ![]() u2 = 16
u2 = 16 ![]() и = ±4; v = 3
и = ±4; v = 3 ![]() и2 = 16
и2 = 16 ![]() и = ±4;
и = ±4;
(для v = -5, v = -3 дійсних значень и не існує).
Звідси відносно и, v система має розв'язки:
![]()
![]()
![]()
![]() u1 = 4 и2 = -4 и3 = 4 u4 = -4
u1 = 4 и2 = -4 и3 = 4 u4 = -4
v1 = 5; v2 = 5; v3 = 3 ; v4 = 3.
Таким чином, початкова система рівносильна сукупності систем:
![]()
![]()
![]()
![]() x + y = 4 х + у = -4 х + у = 4 х + у = -4
x + y = 4 х + у = -4 х + у = 4 х + у = -4
ху = 5; ху = 5; ху = 3; хy = 3.
Перша і друга системи розв'язків не мають, третя система має розв'язок (1; 3); (3; 1), четверта система має розв'язок ( 1; -3), (-3; -1).
Відповідь: (1; 3); (3; 1); (-1; -3); (-3; -1).
Приклад 3.
![]() Розв'язати систему рівнянь х3 + х3у3 + y3 = 17
Розв'язати систему рівнянь х3 + х3у3 + y3 = 17
ху (х + у) = 6.
Розв' язання.
![]() Дана система симетрична відносно х і у. Запишемо її у вигляді
Дана система симетрична відносно х і у. Запишемо її у вигляді
(х + у) (х2 - ху + у2) + х3у3 = 17
xу(х+у) = 6,
![]() або
або
(х + у) (х2+ у)2 - 3xy) + х3у3 = 17
xу(х+у) = 6,
Узявши
![]() x + y = u
x + y = u
ху = v,
![]() дістанемо
дістанемо
и (u2 – 3v) + v2 = 17
uv = 6
![]() або u3 – 3uv + v3 = 17
або u3 – 3uv + v3 = 17
uv = 6,
![]() або u3 + v3 = 35
або u3 + v3 = 35
u3v3 = 216,
Застосувавши теорему Віета, маємо: a2 - 35а + 216 = 0.
Розв'язавши де рівняння, знаходимо a1 = 27, а2 = 8.
![]()
![]() Тоді u = 3 або u = 2
Тоді u = 3 або u = 2
v = 2 v = 3.
Дану систему рівнянь можна замінити сукупністю рівносильних систем
![]()
![]() x + y = 3 та x + y = 2
x + y = 3 та x + y = 2
xy = 2 ху = 3.
Відповідь. (2; 1), (1; 2).
Приклад 4.
Розв язати систему рівнянь
![]() х3 + x3y3 + y3 =17,
х3 + x3y3 + y3 =17,
х + ху + у = 5.
Розв'язання
Поклавши х + у = и , xy = v, переходимо до системи:
![]() u3 + 3uv +vy3 =17,
u3 + 3uv +vy3 =17,
u + v = 5.
![]()
![]() Звідси маємо: u1 = 3 або u2 = 2
Звідси маємо: u1 = 3 або u2 = 2
v1 = 2 v2 = 3.
![]()
![]() Тоді x + y = 3 або x + y = 2
Тоді x + y = 3 або x + y = 2
ху = 2 ху = 3.
Розв'язками цієї сукупності, а з нею і початкової системи рівнянь, є пари чисел: (1; 2), (2; 1).
Відповідь. (2; 1), (1; 2).
Системи діофантових рівнянь.
Діофант представляє одну із найцікавіших особистостей в історії математики. Ми не знаємо, ким був Діофант, точні роки його життя, не відомі його попередники, які працювали у тій же сфері, що й він.
Дуже цікавою є діяльність Діофанта. До нас дійшло 7 книг із 13, які були об’єднані в «Арифметику». Стиль і зміст цих книг дуже відрізняється від класичних книг з теорії чисел та алгебри, зразки яких ми знаємо з «Начал» Евкліда, лем Архімеда і Аполлонія. «Арифметика», безсумнівно, є результатом багаточисленних досліджень, велика кількість з яких залишилась нам невідомою.
«Арифметика» Діофанта – це збірник задач (їх всього 189), кожна з яких має розв'язок і необхідні пояснення. В збірник входять різноманітні задачі, і їх розв’язки дуже часто не так просто зрозуміти. Діофант практикувався у знаходженні розв’язків невизначених рівнянь вигляду Ax2 + Bx + C = y2, Ax3 + Bx2 + Cx + D = y2, або систем таких рівнянь. Його цікавили тільки додатні цілі числа і раціональні розв’язки. Ірраціональні розв’язки він називав «неможливими» і ретельно підбирав коефіцієнти так, щоб отримати шукані додатні, раціональні розв’язки.
Тому ,зазвичай, довільне невизначене рівняння (але, як правило, з цілими коефіцієнтами)називають «діофантовим», якщо хочуть наголосити на тому, що рівняння слід розв’язувати в цілих числах.
Невизначені рівняння першого степеня почали розглядати математики, приблизно в V столітті. Деякі такі рівняння з двома, трьома невідомими з’явились у зв’язку з проблемами, які виникли в астрономії, наприклад, при розгляді питань, пов’язаних з визначенням періодичного повторення небесних явищ.
В 1624 році була опублікована книга французького математика Баше де Мезирьяка , у якій для розв'язку рівняння


про публікацію авторської розробки
Додати розробку