Завдання-тренажери для підготовки до ДПА з математики для 9 класу
Тренувальні тестові завдання з основних розділів курсу алгебри та геометрії, включаючи різні види текстових задач на відсотки і дроби, вправи на встановлення відповідності між величинами, для повторення та підготовки до державної підсумкової атестації з математики у 9 класі,
Завдання-тренажери для підготовки до ДПА з математики
для 9 класу
Тема: Дії з раціональними виразами
Завдання 1 ( тип 1).
- Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Розв’язання: В кожному виразі відповіді, знаходимо значення виразу:
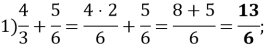
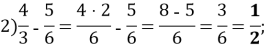
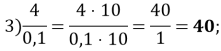
![]()
Порівняємо отримані результати: ![]()
Бачимо, що найменшим є число 0,4. Відповідь: 4.
Розв’язати самостійно:
2. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
3. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
4. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
5. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
6. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
7. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
8. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
9. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
10. Вкажіть вираз, значення якого є найменшим:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Завдання 1 ( тип 2).
-
Якому виразу дорівнює добуток
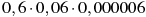 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Розв’язання: Перемножимо дані числа ![]()
![]()
![]()
Далі, перемноживши , отримаємо відповідь: 216![]() . Відповідь: 2
. Відповідь: 2
Розв’язати самостійно:
-
Якому виразу дорівнює добуток
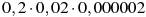 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
-
Якому виразу дорівнює добуток
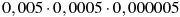 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
-
Якому виразу дорівнює добуток
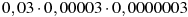 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
-
Якому виразу дорівнює добуток
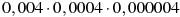 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
-
Якому виразу дорівнює добуток
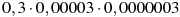 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
-
Якому виразу дорівнює добуток
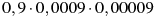 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
-
Якому виразу дорівнює добуток
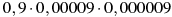 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
-
Якому виразу дорівнює добуток
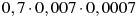 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
|
||||||||||
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
-
Якому виразу дорівнює добуток
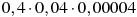 ?
?
Завдання 1 ( тип 3).
1. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
Розв’язання: Виконаємо обчислення:
![]()
![]()
![]()
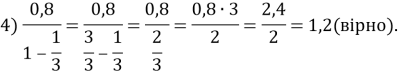
Відповідь: 2; 4.
Розв’язати самостійно:
2. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
10. Запишіть у відповідь номери вірних рівностей:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
Завдання 1 ( тип 4).
1. Для кожного десяткового дробу вкажіть його розклад у вигляді суми розрядних доданків:
А. 0,9024 Б. 9,2004 В. 0,9204
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
Розв’язання А: розкладемо на суму розрядних доданків:
0,9024 = 0,9 + 0,00+ 0,002 + 0,0004= ![]()
Аналогічно перетворюємо кожне число
Б) 9,2004= 9![]()
![]() . Відповідь: А-1, Б – 3, В- 2.
. Відповідь: А-1, Б – 3, В- 2.
Розв’язати самостійно:
2. Для кожного десяткового дробу вкажіть його розклад у вигляді суми розрядних доданків:
А. 0,7407 Б. 7,4007 В. 0,7047
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
3. Для кожного десяткового дробу вкажіть його розклад у вигляді суми розрядних доданків:
А. 0,8402 Б. 8,4002 В. 0,8042
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
4. Для кожного десяткового дробу вкажіть його розклад у вигляді суми розрядних доданків:
А. 0,0573 Б. 0,5073 В. 0,5703
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5. Для кожного десяткового дробу вкажіть його розклад у вигляді суми розрядних доданків:
А. 0,8014 Б. 8,1004 В. 0,8104
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
6. Для кожного десяткового дробу вкажіть його розклад у вигляді суми розрядних доданків:
А. 0,4013 Б. 4,1003 В. 0,4103
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
Тема: Графічна залежність між величинами
Завдання 2.
-
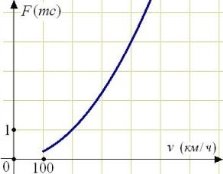 Коли літак знаходиться в горизонтальному польоті, підйомна сила, що діє на крила, залежить тільки від швидкості. На малюнку зображена ця залежність для деякого літака. На осі абсцис відкладається швидкість (в кілометрах в годину), на осі ординат - сила (в тоннах сили). Визначте по малюнку, чому дорівнює підйомна сила (в тоннах сили) при швидкості 200 км /год?
Коли літак знаходиться в горизонтальному польоті, підйомна сила, що діє на крила, залежить тільки від швидкості. На малюнку зображена ця залежність для деякого літака. На осі абсцис відкладається швидкість (в кілометрах в годину), на осі ординат - сила (в тоннах сили). Визначте по малюнку, чому дорівнює підйомна сила (в тоннах сили) при швидкості 200 км /год?
Розв’язання:
По осі Ох знаходимо 200 км / год - що відповідає 2 клітинам, піднімаємося до перетину з графіком і дивимося відповідне значення на осі Оу. Відповідь: 1 (mc).
Розв’язати самостійно:
-

 Коли літак знаходиться в горизонтальному польоті, підйомна сила, що діє на крила, залежить тільки від швидкості. На малюнку зображена ця залежність для деякого літака. На осі абсцис відкладається швидкість (в кілометрах в годину), на осі ординат - сила (в тоннах сили). Визначте по малюнку, чому дорівнює підйомна сила (в тоннах сили) при швидкості 400 км / год?
Коли літак знаходиться в горизонтальному польоті, підйомна сила, що діє на крила, залежить тільки від швидкості. На малюнку зображена ця залежність для деякого літака. На осі абсцис відкладається швидкість (в кілометрах в годину), на осі ординат - сила (в тоннах сили). Визначте по малюнку, чому дорівнює підйомна сила (в тоннах сили) при швидкості 400 км / год?
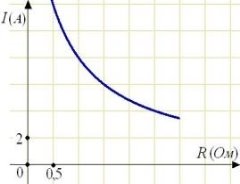
- Потужність обігрівача в автомобілі регулюється додатковим опором, яке можна змінювати, повертаючи рукоятку в салоні машини. При цьому змінюється сила струму в електричному ланцюзі електродвигуна - чим менше опір, тим більше сила струму і тим швидше обертається мотор обігрівача. На малюнку показана залежність сили струму від величини опору. На осі абсцис відкладається опір (в Омах), на осі ординат - сила струму в Амперах. Скільки Ампер становить сила струму в ланцюзі при опорі 0,5 Ом?
-
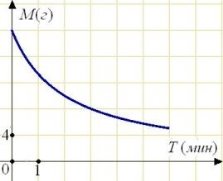
 Під час хімічної реакції кількість вихідної речовини (реагенту), яке ще не вступило в реакцію, згодом поступово зменшується. На малюнку ця залежність представлена графіком. На осі абсцис відкладається час в хвилинах, що минув з моменту початку реакції, на осі ординат - маса залишився реагенту, який ще не вступив в реакцію (в грамах). Визначте за графіком, скільки грамів реагенту було спочатку?
Під час хімічної реакції кількість вихідної речовини (реагенту), яке ще не вступило в реакцію, згодом поступово зменшується. На малюнку ця залежність представлена графіком. На осі абсцис відкладається час в хвилинах, що минув з моменту початку реакції, на осі ординат - маса залишився реагенту, який ще не вступив в реакцію (в грамах). Визначте за графіком, скільки грамів реагенту було спочатку?
-
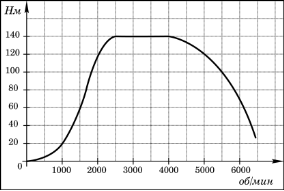
 На графіку зображена залежність крутного моменту двигуна від числа його оборотів в хвилину. На осі абсцис відкладається число оборотів в хвилину, на осі ординат - крутний момент в Н м. Чому дорівнює крутний момент (в Н м), якщо двигун робить 1000 оборотів в хвилину?
На графіку зображена залежність крутного моменту двигуна від числа його оборотів в хвилину. На осі абсцис відкладається число оборотів в хвилину, на осі ординат - крутний момент в Н м. Чому дорівнює крутний момент (в Н м), якщо двигун робить 1000 оборотів в хвилину?
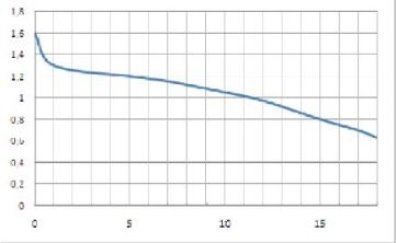
- На малюнку показаний графік розряду батарейки в кишеньковому ліхтарику. На горизонтальній осі відзначається час роботи ліхтарика в годинах, на вертикальній осі - напруга в вольтах. Визначте по малюнку, яка напруга буде давати батарейка через 5 годин роботи ліхтарика. Відповідь дайте у вольтах.
-
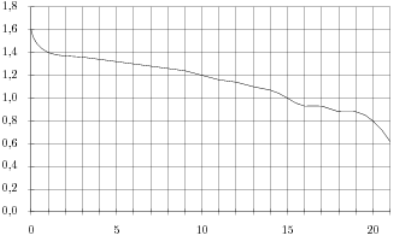 При роботі ліхтарика батарейка часом розрядиться, і напруга в електричному ланцюзі ліхтарика падає. На малюнку показана залежність напруги в ланцюзі від часу роботи ліхтарика. На горизонтальній осі відзначається час роботи ліхтарика в годинах, на вертикальній осі - напруга в вольтах. Визначте по малюнку, яка напруга буде в ланцюзі через 15 годин роботи ліхтарика. Відповідь дайте у вольтах.
При роботі ліхтарика батарейка часом розрядиться, і напруга в електричному ланцюзі ліхтарика падає. На малюнку показана залежність напруги в ланцюзі від часу роботи ліхтарика. На горизонтальній осі відзначається час роботи ліхтарика в годинах, на вертикальній осі - напруга в вольтах. Визначте по малюнку, яка напруга буде в ланцюзі через 15 годин роботи ліхтарика. Відповідь дайте у вольтах.
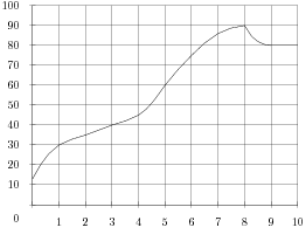
- На графіку показаний процес розігріву двигуна легкового автомобіля. На осі абсцис відкладається час в хвилинах, що минув від запуску двигуна, на осі ординат - температура двигуна в градусах Цельсія. Визначте за графіком, до скількох градусів Цельсія двигун нагрівся за перші 5 хвилин.
Тема: Задачі на знаходження відсотків
Завдання 3.
- Міський бюджет становить 98 млн. грн, а витрати на одну з його статей склали 50%. Скільки грошей витрачено на цю статтю бюджету?
Розв’язання:
1-й спосіб:
98000000 – 100%
? - 50%,
98000000:100![]()
![]()
2 –й спосіб:
50% - половина від 100%, значить 98000000:2= 49000000 (грн.).
Відповідь: 49000000 грн.
Розв’язати самостійно:
- Міський бюджет становить 50 млн. грн, а витрати на одну з його статей склали 35%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 42 млн. грн, а витрати на одну з його статей склали 7,5%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 68 млн. грн, а витрати на одну з його статей склали 22,5%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 97 млн. грн, а витрати на одну з його статей склали 12,5%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 48 млн. грн, а витрати на одну з його статей склали 30%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 67 млн. грн, а витрати на одну з його статей склали 17,5%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 99 млн. грн, а витрати на одну з його статей склали 20%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 69 млн. грн, а витрати на одну з його статей склали 25%. Скільки грошей витрачено на цю статтю бюджету?
- Міський бюджет становить 77 млн. грн, а витрати на одну з його статей склали 10,5%. Скільки грошей витрачено на цю статтю бюджету?
Завдання 4.
- Число хвойних дерев в парку відноситься до числа листяних як 7:13. Скільки відсотків дерев в парку складають листяні?
Розв’язання: Знайдемо загальну кількість частин 7 + 13 = 20 частин;
20ч – 100%
13ч - ? %- листяні; 13![]()
Відповідь: 65%.
Розв’язати самостійно:
2. Число хвойних дерев в парку відноситься до числа листяних як 2:23. Скільки відсотків дерев в парку складають листяні?
3. Число хвойних дерев в парку відноситься до числа листяних як 23:27. Скільки відсотків дерев в парку складають листяні?
4. Число хвойних дерев в парку відноситься до числа листяних як 3:22. Скільки відсотків дерев в парку складають листяні?
5. Число хвойних дерев в парку відноситься до числа листяних як 43:7. Скільки відсотків дерев в парку складають листяні?
6. Число хвойних дерев в парку відноситься до числа листяних як 89:11. Скільки відсотків дерев в парку складають листяні?
7. Число хвойних дерев в парку відноситься до числа листяних як 7:3. Скільки відсотків дерев в парку складають листяні?
8. Число хвойних дерев в парку відноситься до числа листяних як 59:41. Скільки відсотків дерев в парку складають листяні?
9. Число хвойних дерев в парку відноситься до числа листяних як 9:41. Скільки відсотків дерев в парку складають листяні?
10. Число хвойних дерев в парку відноситься до числа листяних як 77:23. Скільки відсотків дерев в парку складають листяні?
Задачі на дроби.
Завдання 5.
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 3/8 всіх повітряних кульок, а в антракті - ще 48 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
Розв’язання: Кількість всіх куль візьмемо за 1, тоді в антракті було продано 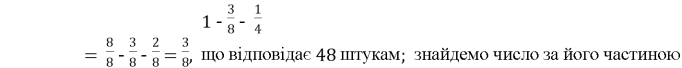
![]() Відповідь: 128.
Відповідь: 128.
Розв’язати самостійно:
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 2/5 всіх повітряних кульок, а в антракті - ще 52 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 2/7 всіх повітряних кульок, а в антракті - ще 64 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 3/7 всіх повітряних кульок, а в антракті - ще 25 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 3/8 всіх повітряних кульок, а в антракті - ще 16 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 4/9 всіх повітряних кульок, а в антракті - ще 64 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 3/8 всіх повітряних кульок, а в антракті - ще 16 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 3/7 всіх повітряних кульок, а в антракті - ще 26 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 2/3 всіх повітряних кульок, а в антракті - ще 18 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 2/7 всіх повітряних кульок, а в антракті - ще 39 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
- Перед виставою в цирку для продажу було заготовлено кілька повітряних кульок. Перед початком вистави було продано 5/8 всіх повітряних кульок, а в антракті - ще 55 штук. Після цього залишилася чверть всіх кульок. Скільки кульок було спочатку?
Задачі про вклади
Завдання 6.
1. Ощадний банк нараховує на строковий вклад 20% річних. Вкладник поклав на рахунок 500 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
Розв’язання: 500 грн. – 100%; 500![]()
Розв’язати самостійно:
- Ощадний банк нараховує на строковий вклад 15% річних. Вкладник поклав на рахунок 1400 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 17% річних. Вкладник поклав на рахунок 1500 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 14% річних. Вкладник поклав на рахунок 1500 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 15% річних. Вкладник поклав на рахунок 900 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 11% річних. Вкладник поклав на рахунок 900 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 20% річних. Вкладник поклав на рахунок 1100 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 12% річних. Вкладник поклав на рахунок 600 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 12% річних. Вкладник поклав на рахунок 900 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
- Ощадний банк нараховує на строковий вклад 25% річних. Вкладник поклав на рахунок 500 грн. Яка сума буде на цьому рахунку через рік, якщо жодна операція з рахунком проводитися не буде?
Задачі на уцінку товару
Завдання 7.
- Товар на розпродажі уцінили на 20%, при цьому він став коштувати 880 грн. Скільки коштував товар до розпродажу?
Розв’язання: ? – 100%
880р. – 80%, 880![]()
Відповідь: 1100 грн.
Розв’язати самостійно:
- Товар на розпродажі уцінили на 50%, при цьому він став коштувати 810 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 20%, при цьому він став коштувати 780 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 50%, при цьому він став коштувати 680 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 20%, при цьому він став коштувати 840 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 25%, при цьому він став коштувати 810 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 40%, при цьому він став коштувати 870 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 15%, при цьому він став коштувати 680 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 50%, при цьому він став коштувати 980 грн. Скільки коштував товар до розпродажу?
- Товар на розпродажі уцінили на 10%, при цьому він став коштувати 840 грн. Скільки коштував товар до розпродажу?
Задачі на прибуток підприємства
Завдання 8.
- Державі належить 80% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 60 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
Розв’язання: 1) 100% - 80%= 20% - приватним особам.
2) 60000000р. – 100%
? - 20%, 0000000![]()
Відповідь: 12000000 грн.
Розв’язати самостійно:
- Державі належить 90% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 80 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Державі належить 90% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 30 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Державі належить 90% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 50 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Державі належить 60% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 40 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам
- Державі належить 60% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 30 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Державі належить 10% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 90 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Державі належить 90% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 20 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Державі належить 80% акцій підприємства, решта акцій належить приватним особам. Загальний прибуток підприємства після сплати податків за рік склав 30 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
Задачі на долі
Завдання 9
- Акції підприємства розподілені між державою і приватними особами у відношенні 3: 5. Загальний прибуток підприємства після сплати податків за рік склав 20 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
Розв’язання: 1) 3 + 5= 8 – всього долей.
2) 20000000: 8 = 2500000 грн – на 1 долю.
3) 2500000![]()
Відповідь: 12500000 грн.
Розв’язати самостійно:
- Акції підприємства розподілені між державою і приватними особами у відношенні 3: 5. Загальний прибуток підприємства після сплати податків за рік склав 77 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Акції підприємства розподілені між державою і приватними особами у відношенні 7: 9. Загальний прибуток підприємства після сплати податків за рік склав 90 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Акції підприємства розподілені між державою і приватними особами у відношенні 6: 5. Загальний прибуток підприємства після сплати податків за рік склав 55 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Акції підприємства розподілені між державою і приватними особами у відношенні 7: 5. Загальний прибуток підприємства після сплати податків за рік склав 27 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Акції підприємства розподілені між державою і приватними особами у відношенні 5: 8. Загальний прибуток підприємства після сплати податків за рік склав 78 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Акції підприємства розподілені між державою і приватними особами у відношенні 3: 2. Загальний прибуток підприємства після сплати податків за рік склав 84 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
- Акції підприємства розподілені між державою і приватними особами у відношенні 3: 5. Загальний прибуток підприємства після сплати податків за рік склав 60 млн. грн. Яка сума з цього прибутку повинна піти на виплату приватним акціонерам?
Тема: Розв’язування лінійних рівнянь
Завдання 10.
-
Розв’язати рівняння:
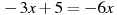
Розв’язання: перенесемо невідомі доданки в ліву частину, відомі доданки в праву частину:
![]()
![]()
![]()
![]()
Відповідь: ![]()
Розв’язати самостійно:
-
Розв’язати рівняння:
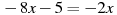 .
.
-
Розв’язати рівняння:
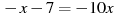
-
Розв’язати рівняння:
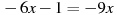
-
Розв’язати рівняння:
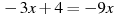 .
.
-
Розв’язати рівняння:
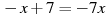
-
Розв’язати рівняння:
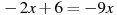 .
.
-
Розв’язати рівняння:
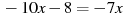
-
Розв’язати рівняння:
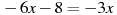 .
.
-
Розв’язати рівняння:
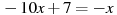
-
Розв’язати рівняння:
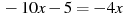 .
.
-
Розв’язати рівняння:
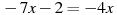 .
.
-
Розв’язати рівняння:
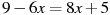 .
.
-
Розв’язати рівняння
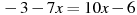
-
Розв’язати рівняння:
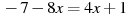
-
Розв’язати рівняння:
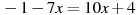
-
Розв’язати рівняння:
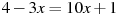 .
.
-
Розв’язати рівняння:
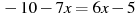
-
Розв’язати рівняння:
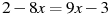
-
Розв’язати рівняння:
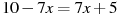 .
.
Тема: Розв’язування раціональних рівнянь
Завдання 11.
-
Розв’язати рівняння:
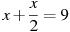 .
.
Розв’язання: Зведемо доданки до спільного знаменника:
![]()
![]()
![]()
![]()
![]()
Розв’язати самостійно:
-
Розв’язати рівняння:
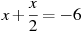 .
.
-
Розв’язати рівняння:
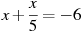 .
.
-
Розв’язати рівняння:
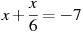 .
.
-
Розв’язати рівняння:
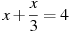 .
.
-
Розв’язати рівняння:
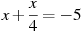 .
.
-
Розв’язати рівняння:
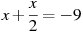 .
.
-
Розв’язати рівняння:
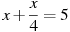 .
.
-
Розв’язати рівняння:
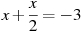 .
.
-
Розв’язати рівняння:
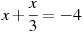 .
.
-
Розв’язати рівняння:
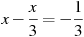 .
.
-
Розв’язати рівняння:
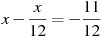 .
.
-
Розв’язати рівняння:
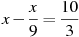 .
.
-
Розв’язати рівняння:
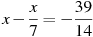 .
.
-
Розв’язати рівняння:
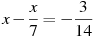 .
.
Тема: Квадратні рівняння
Завдання 12.
-
Розв’язати рівняння:
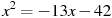 .
.
Розв’язання: 1![]()
скористаємося зворотного теоремою Вієта: 42 розкладемо на множники так,
щоб їх різниця дорівнювала 13; це числа 7 і 6. Тоді х1 = - 6, х2 = - 7. Відповідь: -6; -7.
![]()
![]()
![]() =-6;
=-6; ![]()
![]() Відповідь: -6; -7.
Відповідь: -6; -7.
Розв’язати самостійно:
- х2-3х+2=0
- –х2+2х+8=0
- 2х2-3х+1=0
- х2-х-12=0
- х2+3х-40=0
- –х2-9х-20=0
- х2+3х-28=0
- –х2-16х-63=0
- х2 +9х-22=0
- 6х2-3х-3=0
Тема: Нерівності
Завдання 13 ( тип 1).
-
Одна з точок, позначених на координатній прямій, відповідає числу
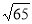 . Яка це точка?
. Яка це точка?
![]()
Розв’язання: 72= 49 ![]()
![]()
![]() .
.
Відповідь: М.
Розв’язати самостійно:
-
Одна з точок, позначених на координатній прямій, відповідає числу
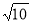 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
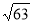 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
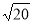 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
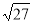 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
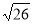 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
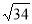 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
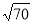 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
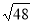 . Яка це точка?
. Яка це точка?
![]()
-
Одна з точок, позначених на координатній прямій, відповідає числу
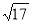 . Яка це точка?
. Яка це точка?
![]()
Завдання 14 ( тип 2).
-
Про числа a і b відомо, що
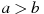 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3)
3) ![]()
Розв’язання:
1) якщо ![]() , то
, то ![]()
![]()
2)![]()
тоді ![]() невірно;
невірно;
3) ми уже вияснили, що ![]()
![]() вірно.
вірно.
Відповідь: 1; 3.
Розв’язати самостійно:
-
Про числа a і b відомо, що
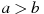 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3)
3) ![]()
-
Про числа a і b відомо, що
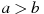 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3 )
3 ) ![]() .
.
-
Про числа a і b відомо, що
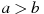 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3)
3) ![]() .
.
-
Про числа a і b відомо, що
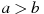 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3)
3) ![]()
-
Про числа a і b відомо, що
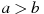 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3)
3) ![]() .
.
-
Про числа a і b відомо, що
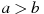 . Серед наведених нижче нерівностей виберіть правильні:
. Серед наведених нижче нерівностей виберіть правильні:
1) ![]() 2)
2) ![]() 3)
3) ![]() .
.
Завдання 15 ( тип 3).
- На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Розв’язання: На координатній прямій видно, що с <а, значить варіант 1) не може бути вірним; 2) при множенні нерівності с <а, на від’ємне число, знак нерівності змінюється, значить нерівність вірна; 3) і 4) якщо до обох частин нерівності додати одне і те ж число, то нерівність вірна або міркувати як в прикладах типу 3 ..
Відповідь: 1.
Розв’язати самостійно:
- На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
- На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
4. На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
5. На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
6. На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
7. На координатній прямій зображені числа а і с. Яка із наступних нерівностей невірна?
![]()
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Завдання 16 ( тип 4 ).
-
Розмістити в порядку зростання числа:
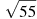 , 7,5,
, 7,5, 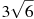 .
.
Розв’язання: Щоб порівняти числа, необхідно їх привести до одного виду:
внесемо під знак кореня числа, які не стоять під коренем.
![]() =
=![]() ;
; ![]() ; тепер порівняємо і запишемо в
; тепер порівняємо і запишемо в
порядку зростання (від меншого до більшого).
Відповідь: ![]()
Розв’язати самостійно:
-
Розмістити в порядку зростання числа: 4,5,
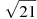 ,
, 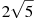 .
.
-
Розмістити в порядку зростання числа:
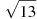 ,
, 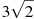 , 3,5.
, 3,5.
-
Розмістити в порядку зростання числа: 5,5,
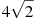 ,
, 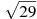 .
.
-
Розмістити в порядку зростання числа:
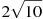 , 6,5,
, 6,5, 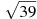 .
.
-
Розмістити в порядку зростання числа:
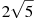 ,
, 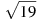 , 4,5.
, 4,5.
-
Розмістити в порядку зростання числа: 6,5,
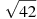 ,
, 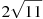 .
.
-
Розмістити в порядку зростання числа:
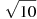 ,
, 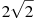 , 3,5.
, 3,5.
-
Розмістити в порядку зростання числа:
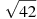 ,
, 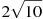 , 6,5.
, 6,5.
-
Розмістити в порядку зростання числа: 4,5,
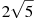 ,
, 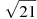 .
.
-
Розмістити в порядку зростання числа: 6,
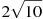 ,
, 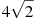 .
.
-
Розмістити в порядку зростання числа:
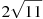 ,
, 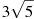 , 6.
, 6.
-
Розмістити в порядку зростання числа: 7,
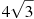 ,
, 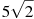 .
.
-
Розмістити в порядку зростання числа:
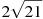 , 9,
, 9, 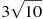 .
.
-
Розмістити в порядку зростання числа: 8,
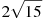 ,
, 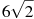
Тема: Властивості степеня
Завдання 17 (тип 1).
-
Знайти значення виразу
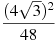 .
.
Розв’язання: ![]() . При піднесенні добутку до степеня,підносимо до цього степеня кожний множник. При піднесенні до квадрату кореня квадратного, отримуємо підкореневий вираз. Відповідь: 1.
. При піднесенні добутку до степеня,підносимо до цього степеня кожний множник. При піднесенні до квадрату кореня квадратного, отримуємо підкореневий вираз. Відповідь: 1.
Розв’язати самостійно:
-
Знайти значення виразу
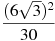 .
.
-
Знайти значення виразу
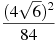 .
.
-
Знайти значення виразу
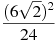 .
.
-
Знайти значення виразу
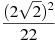 .
.
-
Знайти значення виразу
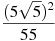 .
.
-
Знайти значення виразу
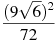 .
.
-
Знайти значення виразу
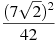 .
.
-
Знайти значення виразу
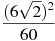 .
.
-
Знайти значення виразу
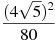 .
.
-
Знайти значення виразу
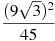 .
.
-
Знайти значення виразу
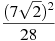 .
.
-
Знайти значення виразу
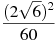 .
.
-
Знайти значення виразу
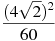 .
.
-
Знайти значення виразу
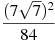 .
.
Завдання 18 ( тип 2).
-
Який із виразів дорівнює
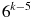 ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Розв’язання: Скористаємося властивостями степеня: показники віднімаються при діленні, тоді представимо наш вираз у вигляді частки ![]() Тепер ми бачимо, що такий вираз стоїть під номером 2.
Тепер ми бачимо, що такий вираз стоїть під номером 2.
Відповідь: 2.
Розв’язати самостійно:
2. Який із виразів дорівнює ![]() ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
3. Який із виразів дорівнює ![]() ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
4. Який із виразів дорівнює ![]() ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
5. Який із виразів дорівнює ![]() ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
6. Який із виразів дорівнює ![]() ?
?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Завдання 19 ( тип 3).
-
Подати вираз
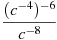 у вигляді степеня з основою c.
у вигляді степеня з основою c.
Розв’язання: Застосуємо властивості степеня: при піднесені степеня до степеня показники перемножаються, при діленні – віднімаються:
![]() . Відповідь:
. Відповідь: ![]()
Розв’язати самостійно:
-
Подати вираз
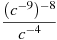 у вигляді степеня з основою c.
у вигляді степеня з основою c.
-
Подати вираз
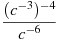 у вигляді степеня з основою c.
у вигляді степеня з основою c.
-
Подати вираз
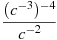 у вигляді степеня з основою c.
у вигляді степеня з основою c.
-
Подати вираз
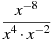 у вигляді степеня з основою х.
у вигляді степеня з основою х.
-
Подати вираз
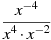 у вигляді степеня з основою х..
у вигляді степеня з основою х..
-
Подати вираз
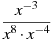 у вигляді степеня з основою x.
у вигляді степеня з основою x.
-
Подати вираз
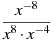 у вигляді степеня з основою х.
у вигляді степеня з основою х.
-
Знайти значення виразу
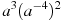 при
при  .
.
-
Знайти значення виразу
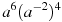 при
при  .
.
-
Знайти значення виразу
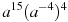 при
при  .
.
Тема: Застосування теореми Піфагора
Завдання 20.
- Хлопчик пройшов від будинку на схід 450 м. Потім повернув на північ і пройшов 240 м. На якій відстані (в метрах) від будинку виявився хлопчик?
Розв’язання: Якщо проаналізувати рух хлопчика, то ми побачимо, що він йшов по катетам прямокутного трикутника. Тоді знайти треба гіпотенузиу (відстань від будинку до місця, де виявився хлопчик).
АВ = ![]() =450м
=450м
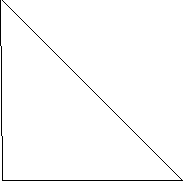 =
=![]() А
А
Відповідь: 510м.
450м ?
Розв’язати самостійно: 240м
С В
1. Хлопчик пройшов від будинку по напрямку на схід 120 м. Потім повернув на північ і пройшов 50 м. На якій відстані (в метрах) від будинку виявився хлопчик?
2. Хлопчик пройшов від будинку по напрямку на схід 560 м. Потім повернув на північ і пройшов 420 м. На якій відстані (в метрах) від будинку виявився хлопчик?
3. Хлопчик пройшов від будинку по напрямку на схід 400 м. Потім повернув на північ і пройшов 300 м. На якій відстані (в метрах) від будинку виявився хлопчик?
4. Хлопчик пройшов від будинку по напрямку на схід 990 м. Потім повернув на північ і пройшов 200 м. На якій відстані (в метрах) від будинку виявився хлопчик?
Завдання 21.
- Дівчинка пройшла від будинку по напрямку на захід 820 м. Потім повернула на північ і пройшла 160 м. Після цього вона повернула на схід і пройшла ще 700 м. На якій відстані (в метрах) від будинку виявилася дівчинка?
Розв’язання: Ми знаємо, що захід і північ знаходяться один до одного під прямим кутом.
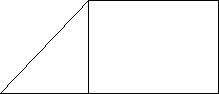 А 700м В Треба знайти АД.
А 700м В Треба знайти АД.
ДН= 820 – 700 = 120;
160м
Д Н 820м С ![]()
АН = ВС = 160м
По т. Піфагора АД = ![]() Відповідь: 200м.
Відповідь: 200м.
Розв’язати самостійно:
1. Дівчинка пройшла від будинку по напрямку на захід 980 м. Потім повернула на північ і пройшла 280 м. Після цього вона повернула на схід і пройшла ще 980 м. На якій відстані (в метрах) від будинку виявилася дівчинка?
2. Дівчинка пройшла від будинку по напрямку на захід 480 м. Потім повернула на північ і пройшла 720 м. Після цього вона повернула на схід і пройшла ще 480 м. На якій відстані (в метрах) від будинку виявилася дівчинка?
3. Дівчинка пройшла від будинку по напрямку на захід 120 м. Потім повернула на північ і пройшла 320 м. Після цього вона повернула на схід і пройшла ще 720 м. На якій відстані (в метрах) від будинку виявилася дівчинка?
3. Дівчинка пройшла від будинку по напрямку на захід 380 м. Потім повернула на північ і пройшла 180 м. Після цього вона повернула на схід і пройшла ще 380 м. На якій відстані (в метрах) від будинку виявилася дівчинка?
4. Дівчинка пройшла від будинку по напрямку на захід 160 м. Потім повернула на північ і пройшла 80 м. Після цього вона повернула на схід і пройшла ще 220 м. На якій відстані (в метрах) від будинку виявилася дівчинка?
Тема: Задачі на подібність
Завдання 22.
- Людина ростом 1,5 м коштує на відстані 16 кроків від стовпа, на якому висить ліхтар. Тінь людини дорівнює чотирьом крокам. На якій висоті (в метрах) розташований ліхтар?
Розв’язання: Д
![]()
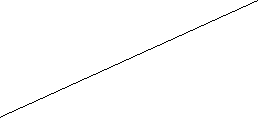 ВЕ = 1,5 м; СД= ?; ВС = 16 ш; АВ = 4 ш.
ВЕ = 1,5 м; СД= ?; ВС = 16 ш; АВ = 4 ш.
![]()
![]()
прямокутні).
![]() А
А
В С
Тоді АС = 16+4=20;
![]() ;
; ![]() Відповідь: 7,5 м.
Відповідь: 7,5 м.
Розв’язати самостійно:
- Людина зростом 1,8 м стоїть на відстані 9 кроків від стовпа, на якому висить ліхтар. Тінь людини дорівнює трьом крокам. На якій висоті (в метрах) розташований ліхтар?
- Людина ростом 1,8 м стоїть на відстані 6 кроків від стовпа, на якому висить ліхтар. Тінь людини дорівнює трьом крокам. На якій висоті (в метрах) розташований ліхтар?
- Людина ростом 1,5 м стоїть на відстані 8 кроків від стовпа, на якому висить ліхтар. Тінь людини дорівнює п'яти крокам. На якій висоті (в метрах) розташований ліхтар?
- Людина ростом 1,8 м стоїть на відстані 16 кроків від стовпа, на якому висить ліхтар. Тінь людини дорівнює восьми кроків. На якій висоті (в метрах) розташований ліхтар?
- Людина ростом 1,5 м стоїть на відстані 12 м від стовпа, на якому висить ліхтар на висоті 3,3 м. Знайдіть довжину тіні людини в метрах.
- Людина ростом 1,8 м стоїть на відстані 12 м від стовпа, на якому висить ліхтар на висоті 5,4 м. Знайдіть довжину тіні людини в метрах.
- .Людина ростом 1,9 м стоїть на відстані 16 м від стовпа, на якому висить ліхтар на висоті 9,5 м. Знайдіть довжину тіні людини в метрах.
- Людина ростом 1,5 м стоїть на відстані 13 м від стовпа, на якому висить ліхтар на висоті 8 м. Знайдіть довжину тіні людини в метрах.
- Людина ростом 1,5 м стоїть на відстані 5 м від стовпа, на якому висить ліхтар на висоті 4 м. Знайдіть довжину тіні людини в метрах.
Тема: Знаходження площі та елементів фігури
Завдання 23.
- Площа прямокутної земельної ділянки дорівнює 11 га, ширина ділянки дорівнює 100 м. Знайдіть довжину цієї ділянки в метрах.
Розв’язання: Так як ділянка прямокутна,
то його Ѕ= a![]()
тоді a = 110000:100 = 1100м. Відповідь: 1100м.
Розв’язати самостійно:
- Площа прямокутної земельної ділянки дорівнює 20 га, ширина ділянки дорівнює 200 м. Знайдіть довжину цієї ділянки в метрах.
- Площа прямокутної земельної ділянки дорівнює 18 га, ширина ділянки дорівнює 240 м. Знайдіть довжину цієї ділянки в метрах.
- Площа прямокутної земельної ділянки дорівнює 19 га, ширина ділянки дорівнює 400 м. Знайдіть довжину цієї ділянки в метрах.
- Знайдіть периметр прямокутної ділянки землі, площа якого дорівнює 800 м2 і одна сторона в 2 рази більша за іншу. Відповідь дайте у метрах.
- Знайдіть периметр прямокутної ділянки землі, площа якого дорівнює 7500 м2і одна сторона в 3 рази більша за іншу. Відповідь дайте у метрах.
- Знайдіть периметр прямокутної ділянки землі, площа якого дорівнює 24500 м2 і одна сторона в 5 разів більша за іншу. Відповідь дайте у метрах.
- Підлогу кімнати, що має форму прямокутника зі сторонами 4 м і 10 м, потрібно покрити паркетом з прямокутних дощечок зі сторонами 5 см і 20 см. Скільки потрібно таких дощечок?
- Підлогу кімнати, що має форму прямокутника зі сторонами 5 м і 8 м, потрібно покрити паркетом з прямокутних дощечок зі сторонами 5 см і 40 см. Скільки потрібно таких дощечок?
- Підлогу кімнати, що має форму прямокутника зі сторонами 3 м і 9 м, потрібно покрити паркетом з прямокутних дощечок зі сторонами 5 см і 30 см. Скільки потрібно таких дощечок?
- Підлогу кімнати, що має форму прямокутника зі сторонами 7 м і 8 м, потрібно покрити паркетом з прямокутних дощечок зі сторонами 10 см і 40 см. Скільки потрібно таких дощечок?
- Підогу кімнати, що має форму прямокутника зі сторонами 4 м і 6 м, потрібно покрити паркетом з прямокутних дощечок зі сторонами 10 см і 30 см. Скільки потрібно таких дощечок?
- Скільки потрібно кахельних плиток квадратної форми зі стороною 15 см, щоб облицювати ними стіну, що має форму прямокутника зі сторонами 2,7 м і 3 м?
- Скільки потрібно кахельних плиток квадратної форми зі стороною 20 см, щоб облицювати ними стіну, що має форму прямокутника зі сторонами 2,8 м і 5 м?
- Скільки потрібно кахельних плиток квадратної форми зі стороною 20 см, щоб облицювати ними стіну, що має форму прямокутника зі сторонами 2,6 м і 3,6 м?
Завдання 24.
- Дві труби, діаметри яких дорівнюють 6 см і 8 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
Розв’язання: За умовою задачі нова труба повинна мати
Ѕ=Ѕ1+ Ѕ2; Ѕ= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Розв’язати самостійно:
- Дві труби, діаметри яких дорівнюють 16 см і 63 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 48 см і 55 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 9 см і 12 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 40 см і 75 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 30 см і 40 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 66 см і 88 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 56 см і 90 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 13 см і 84 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 16 см і 30 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 13 см і 84 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
- Дві труби, діаметри яких дорівнюють 16 см і 30 см, потрібно замінити однією, не змінюючи пропускну здатність. Яким повинен бути діаметр нової труби? Відповідь дайте у сантиметрах.
Завдання 25.
- Скільки дощок довжиною 2 м, шириною 20 см і товщиною 10 мм вийде з чотирикутної балки довжиною 100 дм, що має в перетині прямокутник розміром 50 см * 80 см?
Розв’язання: Знайдемо площу дошки: 2 ∙ 0,2 ∙ 0,001 = 0,0004м2, площа балки: 10 ∙ 0,5 ∙ 0,8 = 4м2; знайдемо кількість дощок: 4: 0,0004 = 40000: 4 = 10000 досок. Відповідь: 10000 досок.
Розв’язати самостійно:
- Скільки дощок довжиною 3 м, шириною 10 см і товщиною 10 мм вийде з чотирикутної балки довжиною 120 дм, що має в перерізі прямокутник розміром 30 см* 70 см?
- Скільки дощок довжиною 3 м, шириною 20 см і товщиною 15 мм вийде з чотирикутної балки довжиною 120 дм, что має в перерізі прямокутник розміром 30 см* 80 см?
- Скільки дощок довжиною 3 м, шириною 30 см і товщиною 20 мм вийде з чотирикутної балки довжиною 150 дм, що має в перерізі прямокутник розміром 50 см* 60 см?
- Скільки дощок довжиною 2,5 м, шириною 30 см і товщиною 20 мм вийде з чотирикутної балки довжиною 50 дм, що має в перерізі прямокутник розміром 40 см* 60 см?
- Скільки дощок довжиною 3,5 м, шириною 10 см і товщиною 25 мм вийде з чотирикутної балки довжиною 70 дм, що має в перерізі прямокутник розміром 50 см * 80 см?
- Скільки дощок довжиною 3 м, шириною 30 см і товщиною 15 мм вийде з чотирикутної балки довжиною 120 дм, що має в перерізі прямокутник розміром 30 см * 60 см?
- Скільки дощок довжиною 3,5 м, шириною 20 см і товщиною 25 мм вийде з чотирикутної балки довжиною 70 дм, що має в перерізі прямокутник розміром 40 см * 60 см?
- Скільки дощок довжиною 3 м, шириною 15 см і товщиною 25 мм вийде з чотирикутної балки довжиною 150 дм, що має в перерізі прямокутник розміром 30 см * 60 см?
- Скільки дощок довжиною 3 м, шириною 10 см і товщиною 10 мм вийде з чотирикутної балки довжиною 90 дм, що має в перерізі прямокутник розміром 40 см * 60 см?
Тема: Теорія ймовірності
Завдання 26.
- Андрій вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 33.
Розв’язання: Всього тризначних чисел 999- 99 = 900; з них на 33 діляться (132+ 33 ∙ (n-1)) = 990; 990; (999: 33 = 30 і 7 в остачі, тоді 33 ∙ 30 = 990, по формулі n-го члена арифметичної прогресії); 33n = 990 - (132 -33); 33n = 891; n = 27; Таким чином ймовірність Р = 27/900 = 0,03; Відповідь: 0,03.
Розв’язати самостійно:
2. Коля вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 4.
3. Андрій вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 10.
4. Коля вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 93.
5. Максим вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 98.
6. Женя вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 2.
7. Стас вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 20.
8. Вова вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 49.
9. Валя вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 50.
10. Женя вибирає тризначне число. Знайдіть ймовірність того, що воно ділиться на 52.
11. Телевізор у Марини зламався і показує тільки один випадковий канал. Марина вмикає телевізор. В цей час по восьми каналах з сорока показують кінокомедії. Знайдіть ймовірність того, що Марина потрапить на канал, де комедія не йде. Пояснення: 40 - 8 = 32; Р = 32/40 = 0, 8. Відповідь: 0,8.
12. Телевізор у Саші зламався і показує тільки один випадковий канал. Саша вмикає телевізор. В цей час по п'ятнадцяти каналах з п'ятдесяти показують кінокомедії. Знайдіть ймовірність того, що Саша потрапить на канал, де комедія не йде.
13.Телевізор у Олі зламався і показує тільки один випадковий канал. Оля вмикає телевізор. В цей час по семи каналах з двадцяти одного показують новини. Знайдіть ймовірність того, що Оля потрапить на канал, де новини не йдуть.
14.Телевізор у Колі зламався і показує тільки один випадковий канал. Коля вмикає телевізор. В цей час по дев'яти каналам з двадцяти одного показують новини. Знайдіть ймовірність того, що Коля потрапить на канал, де новини не йдуть.
15. На тарілці 20 пиріжків: 2 з м'ясом, 16 з капустою і 2 з вишнею. Рома навмання вибирає один пиріжок. Знайдіть ймовірність того, що він виявиться з вишнею.
16. На тарілці 10 пиріжків: 5 з м'ясом, 2 з капустою і 3 з вишнею. Андрій навмання вибирає один пиріжок. Знайдіть ймовірність того, що він виявиться з вишнею.
17.У фірмі таксі в даний момент вільно 15 машин: 3 чорних, 6 жовтих і 6 зелених. За викликом виїхала одна з машин, що випадково опинилася найближче до замовника. Знайдіть ймовірність того, що до нього приїде жовте таксі.
18. Маша з татом вирішили покататися на колесі огляду. Всього на колесі п'ятнадцять кабінок, з них 2 - сині, 10 - зелені, інші - червоні. Кабінки по черзі підходять до платформи для посадки. Знайдіть ймовірність того, що Маша буде кататися в червоній кабінці.
19.У бабусі 10 чашок: 8 з червоними квітами, інші з синіми. Бабуся наливає чай в випадково вибрану чашку. Знайдіть ймовірність того, що це буде чашка з синіми кольорами.
20. На іспиті 40 квитків, Сеня не вивчив 8 з них. Знайдіть ймовірність того, що йому попадеться невивчений квиток.
21. На іспиті 20 квитків, Андрій не вивчив 1 з них. Знайдіть ймовірність того, що йому попадеться невивчений квиток.
22. Батьківський комітет закупив 20 пазлів для подарунків дітям на закінчення року, з них 11 з машинами і 9 з видами міст. Подарунки розподіляються випадковим чином. Знайдіть ймовірність того, що Іллі дістанеться пазл з машиною.
23. Батьківський комітет закупив 25 пазлів для подарунків дітям на закінчення року, з них 19 з машинами і 6 з видами міст. Подарунки розподіляються випадковим чином. Знайдіть ймовірність того, що Віті дістанеться пазл з машиною.
24. В середньому на 50 кишенькових ліхтариків припадає п'ять несправних. Знайдіть ймовірність купити працюючий ліхтарик.
25.В середньому на 100 кишенькових ліхтариків припадає дев'ять несправних. Знайдіть ймовірність купити працюючий ліхтарик.
26. У середньому з кожних 150 які надійшли на продаж 120 акумуляторів заряджені. Знайдіть ймовірність того, що куплений акумулятор не заряджений.
27. В середньому з кожних 100 щонадійшли на продаж 96 акумуляторів заряджені. Знайдіть ймовірність того, що куплений акумулятор не заряджений. 28. Стьопа навмання вибирає двозначне число. Знайдіть ймовірність того, що воно починається на 8.
29. Максим навмання вибирає двозначне число. Знайдіть ймовірність того, що воно починається на 3.
30.Андрій навмання вибирає двозначне число. Знайдіть ймовірність того, що воно закінчується на 5.
Тема: Відповідність між графіком та функцією.
Завдання 27.
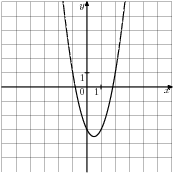
1. Графік якої з наведених нижче функцій зображений на малюнку?
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Розв’язання: На малюнку зображено графік квадратичної функції, вітки параболи напрямлені вгору, координати точки перетину з віссю Оу- (0; -3). 1 і 2 не підходить так як вітки напрямлені вгору; залишається вибір з 3 і 4; координати перетину з віссю Ох: для 3) 2х2 + 2х -3 = 0; по теоремі Вієта х1 ∙ х2 = -3, х1 + х2 = -в, по малюнку корені протилежні і більший корінь додатній, значить в має знак «-2».
Значить зображена функція 4. Відповідь: 4.
Розв’язати самостійно:
- Графік якої з наведених нижче функцій зображений на малюнку?
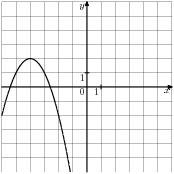
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
- Графік якої з наведених нижче функцій зображений на малюнку?
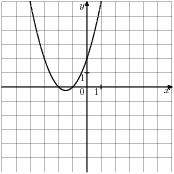
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
- Графік якої з наведених нижче функцій зображений на малюнку?
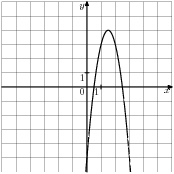
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
- Графік якої з наведених нижче функцій зображений на малюнку?
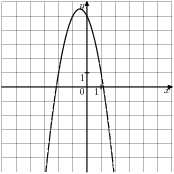
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
-
Знайдіть значення
 користуючись графіком
користуючись графіком 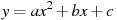 , зображеному на малюнку.
, зображеному на малюнку.
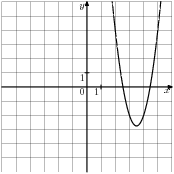
|
1. |
34 |
|
2. |
3 |
|
3. |
-21 |
|
4. |
-3 |
Розв’язання: Вітки параболи напрямлені вгору, значить а- додатній коефіцієнт і відповіді 3, 4 не підходять; вибір з відповідей 1 і 2. За графіком видно, що від вершини параболи або осі симетрії: при х = 1, у = 3 і а = 3: 1 = 3. Відповідь: 2.
Розв’язати самостійно:
-
Знайдіть значення
 користуючись графіком
користуючись графіком 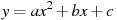 , зображеному на малюнку.
, зображеному на малюнку.
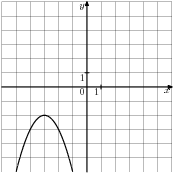
|
1. |
1 |
|
2. |
-11 |
|
3. |
-6 |
|
4. |
-1 |
-
Знайдіть значення
 користуючись графіком
користуючись графіком 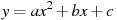 , зображеному на малюнку.
, зображеному на малюнку.
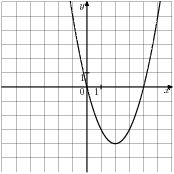
|
1. |
0 |
|
2. |
-1 |
|
3. |
1 |
|
4. |
-4 |
-
Знайдіть значення
 користуючись графіком
користуючись графіком 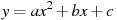 , зображеному на малюнку.
, зображеному на малюнку.
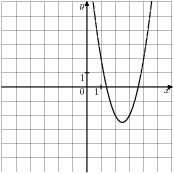
|
1. |
-10 |
|
2. |
-2 |
|
3. |
2 |
|
4. |
10 |
-
Знайдіть значення
 користуючись графіком
користуючись графіком 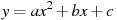 , зображеному на малюнку.
, зображеному на малюнку.
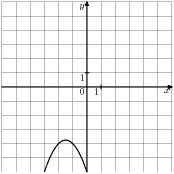
|
1. |
-6 |
|
2. |
-1 |
|
3. |
-3 |
|
4. |
1 |
Тема: Знаходження значення виразу
Завдання 28.
-
Знайти значення виразу
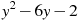 при
при 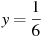 .
.
Розв’язання: Підставимо у вираз числове значення змінної:
![]()
Відповідь: ![]()
Розв’язати самостійно:
-
Знайти значення виразу
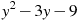 при
при 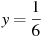 .
.
-
Знайти значення виразу
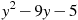 при
при 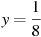 .
.
-
Знайти значення виразу
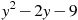 при
при 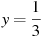 .
.
-
Знайти значення виразу
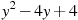 при
при 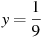 .
.
-
Знайти значення виразу
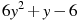 при
при 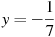 .
.
-
Знайти значення виразу
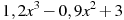 при
при 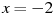 .
.
-
Знайти значення виразу
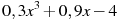 при
при 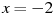 .
.
-
Знайти значення виразу
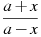 при
при 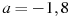 ,
, 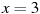 .
.
-
Знайти значення виразу
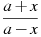 при
при 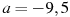 ,
, 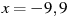
-
Знайти значення виразу
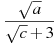 при
при 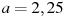 ;
; 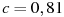 .
.
-
Найдите значение выражения
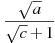 при
при 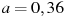 ;
; 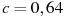 .
.
-
Знайти значення виразу
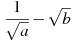 при
при 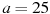 ;
; 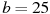 .
.
-
Знайти значення виразу
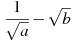 при
при 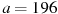 ;
; 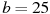 .
.
-
Знайти значення виразу
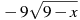 при
при 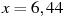 .
.


про публікацію авторської розробки
Додати розробку
