Матеріали для проведення факультативних занять з теми "Симетрія""

 

 

КЗ «Пономаренківський  ліцей»

Роганської селищної ради Харківського району

Харківської області

 

 

 

 

 

«КРАСА ВРЯТУЄ СВІТ»

(СИМЕТРІЯ ТА АСИМЕТРІЯ)

 

 

 

 

 

Казьмірова Олена Іванівна

учитель вищої кваліфікаційної категорії

вчитель – методист

 

 

 

 

 

 

 

 

м. Харків

 

 

ЗМІСТ

 

 

ВСТУП………………………………………………………………..……….……3

РОЗДІЛ 1  ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ………………………….…6

1.            Основні поняття симетрії…………………………….……....….….6
2.            Зв'язок між поняттями симетрії та асиметрії ……….………..….10

РОЗДІЛ 2  СИМЕТРІЯ ТА АСИМЕТРІЯ НАВКРУГ НАС……….….…..….. 14

2.1.  «Золотий переріз» у гармонії життя……………… …………...…. 14 

2.2.  Чи важливі симетрія і асиметрія в професії дизайнера? …….….. 33 

2.3.  Симетрія і асиметрія в природі……………………………………..37 

РОЗДІЛ 3  СИМЕТРІЯ В ОСНОВІ ВСЬОГО: В МАТЕМАТИЦІ, ФІЗИЦІ, ХІМІЇ, БІОЛОГІЇ, СИМЕТРІЯ ПРОСТОРУ ТА ЧАСУ…………………….…42 

ВИСНОВОК……………………………………………………………..….……44

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ………………………………..…..…..47

 

 

 

 

 

 

 

 

 

ВСТУП

«Краса врятує світ»

Ф.І. Достоєвський

З давніх давен людина прагне оточувати себе гарними речами.  Вже предмети побуту мешканців давнини, які, здавалося б, переслідували практичну мету - служити сховищем води, зброєю на полюванні і т. д. демонструють прагнення людини до краси. На певному етапі свого розвитку людина почала шукати відповіді на запитання: чому той чи інший предмет є гарним і що є основою прекрасного? Вже в Стародавній Греції вивчення сутності краси, прекрасного, сформувалося в самостійну гілку науки - естетику, яка у античних філософів була невіддільна від космології. Тоді ж народилося уявлення про те, що основою прекрасного є гармонія.

Минули тисячоліття, перш ніж людство на шляху своєї суспільно-виробничої діяльності усвідомило необхідність виразити в певних поняттях встановлені ним перш за все в природі дві тенденції: наявність суворої упорядкованості, пропорційності, рівноваги та їх порушення. 

 Люди давно звернули увагу на правильність форми кристалів,геометричну строгість будови бджолиних стільників, послідовність  і повторюваність розташування гілок і листя на деревах, пелюсток, квітів, насіння рослин і відобразили цю впорядкованість у своїй практичній діяльності, мисленні та мистецтві. 
        Поняття «симетрія» вживалося у двох значеннях. В одному сенсі симетричне означало щось пропорційне; симетрія показує той спосіб узгодження багатьох частин, з допомогою якого вони об'єднуються в ціле. Другий сенс цього слова - рівновага. 
         Грецьке слово означає однорідність, відповідність, пропорційність, гармонію. 

Існує старовинна притча про буриданового віслюка.

Буриданів осел — вислів, що характеризує людину, яка перебуває у крайній нерішучості та не знає, яке прийняти рішення.

Ще грецький філософ Арістотель висловив думку, що людина, зіткнувшись з проблемою вибору між рівноцінними речами або подіями, довго вагається і не знає, чому віддати перевагу. Пізніше французький філософ Жан Буридан розвинув цю теорію і для наочності навів приклад осла, який, перебуваючи на рівній відстані між двома однаковими оберемками сіна, наражається на небезпеку померти з голоду, бо через свою нерішучість не може віддати перевагу одному із них.

Так, простоявши на одному місці й ані на крок не зсунувшись у той або інший бік, осел одержав «заслужену нагороду» — голодну смерть.

    

Карикатура початку 20 століття(рис.1), де США зображена як                                                                буриданів осел, що обирає між Панамою та Нікарагуа як                                                                                                            місцем для майбутнього каналу

 

 

 

рис. 1

Краса скульптури, краса храму, краса картини, симфонії, поеми ... Що між ними спільного? Хіба можна порівнювати красу храму з красою ноктюрну? Виявляється можна, якщо будуть знайдені єдині критерії прекрасного, якщо будуть відкриті загальні формули краси, що поєднують поняття прекрасного самих різних об'єктів - від квітки ромашки до краси людського тіла. Якщо розглядати природні і створені людиною творіння, то можна знайти єдність і порядок, властиві всім цим предметам. Цей порядок і єдність і є Гармонія, визначальна Краси. Проблемі симетрії присвячена воістину неозора література. В "Короткому Оксфордському словнику" симетрія визначається як "краса, обумовлена ​​пропорційністю частин тіла або якого цілого, рівновагою, подобою, гармонією, узгодженістю" (сам термін "симетрія" з грецької  означає "відповідність", яку стародавні філософи розуміли як окремий випадок гармонії - узгодження частин у рамках цілого). Симетрія є однією з найбільш фундаментальних і однією з найбільш загальних закономірностей світобудови: неживої, живої природи і суспільства. З симетрією ми зустрічаємося всюди. Поняття симетрії проходить через всю багатовікову історію людської творчості. Воно зустрічається вже біля витоків людського знання, його широко використовують усі без винятку напрямки сучасної науки.

Прикладом дивного поєднання симетрії і асиметрії є Покровський собор (храм Василя Блаженного) на Красній площі в Москві. Ця химерна композиція з десяти храмів, кожен з яких має центральну симетрію, в цілому не має ні дзеркальної, ні поворотної симетрії. Симетричні архітектурні деталі собору кружляють у своєму асиметричному, безладному танці навколо його центрального намету: вони то піднімаються, то опускаються, то як би набігають один на одного, то відстають, створюючи враження радості і свята. Без своєї дивовижної асиметрії храм Василя Блаженного просто немислимий! Як і в будь-якій справі, абсолютизація однієї ідеї не могла привести ні до чого хорошого. Симетрія в мистецтві не склала винятку. "Краса неправильна", асиметрія, стала пробивати собі дорогу в мистецтві, бо зведення краси тільки до симетрії обмежувало багатство її внутрішнього змісту, позбавляло красу життя. Істинну красу можна осягнути тільки в єдності протилежностей. Ось чому саме єдність симетрії і асиметрії визначає сьогодні внутрішній зміст прекрасного в мистецтві. Симетрія сприймається нами як спокій, скутість, закономірність, тоді як асиметрія означає рух, свободу, випадковість. Отже, "сфера впливу" симетрії (а значить, її антипода-асиметрії), воістину безмежна. Природа - наука - мистецтво. Усюди ми бачимо протиборство, а часто і єдність двох великих начал - симетрії і асиметрії, які багато в чому і визначають гармонію природи, мудрість науки і красу мистецтва.

 

 

 

 

 

 

 

 

РОЗДІЛ 1.

ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

1.1 Основні поняття

Симетрія (від грецького symmetria - домірність), в широкому сенсі - інваріантність (незмінність) структури, властивостей, форми (напрям в геометрії, кристалографії) матеріального об’єкта щодо його перетворень (тобто змін ряду фізичних властивостей). Симетрія лежить в основі збереження законів. У “Короткому Оксфордському словнику” симетрія визначається як “краса, обумовлена ​​пропорційністю частин тіла або будь-якого цілого, рівновагою, подобою, гармонією, узгодженістю”
        У найбільш загальному вигляді під “симетрією” в математиці розуміється таке перетворення простору (площини), при якому кожна точка M переходить в іншу точку M₁ відносно  деякої площини (або прямої) a, коли відрізок MM₁ є перпендикулярним площині (або прямій) a і ділиться нею навпіл. Площина (пряма) a називається при цьому площиною (або віссю) симетрії.

Симетрія - це категорія, що позначає процес існування та становлення тотожних моментів в певних умовах і в певних відносинах між різними і протилежними станами явищ світу.

Чи справді є загальним сформульоване нами визначення поняття симетрії, чи охоплює воно всі відомі нам форми прояву симетрії як в об'єктивному світі, так і в процесі нашого пізнання?

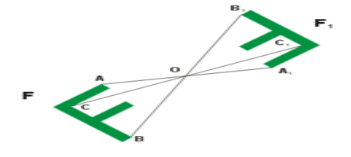
 Очевидно, що при відповіді на це питання доведеться обмежитися тільки найбільш загальними характерними прикладами. Уявімо собі дві точки, що знаходяться по відношенню до якоїсь прямої на її протилежних сторонах; якщо ці протилежні точки рівновіддалені від цієї прямої, то про них говорять як про симетричні по відношенню до даної прямої. Якщо ми тепер зробимо операцію перегину, то в результаті наші точки повністю співпадуть, зіллються один з одним, отже, можна говорити про їх повну тотожність. Симетрія розташування даних точок вказує саме на те, за  яких  процесів і за яких умов вони стають тотожними.

До фундаментальних понять симетрії відносяться площина симетрії, вісь симетрії, центр симетрії. Площиною симетрії P називається така площина, яка ділить фігуру на дві дзеркально рівні частини, розташовані один відносно одного так, як предмет і його дзеркальне відображення. Наприклад, зображений на Рис.2а зліва рівнобедрений трикутник ABC висотою BD поділяється на дві дзеркально рівні половини ABD і BCD; при цьому висота BD є “слідом” площини симетрії P, перпендикулярної площині трикутника. На рис. 2б праворуч зображено також прямокутний паралелепіпед (цеглинка, сірникова коробка), який має три взаємно перпендикулярні площини симетрії 3P. Неважко встановити, що куб володіє дев’ятьма площинами симетрії - 9P.

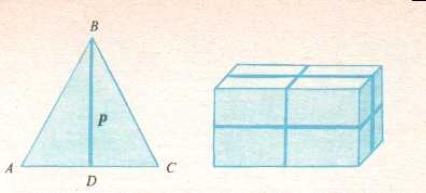
Рисунок 2. Симетрія трикутника (а)і “цеглинки” (б).

Центром симетрії C називається така особлива точка всередині фігури, що характеризується тим, що будь-яка проведена через точку пряма по обидві сторони від неї і на рівних відстанях зустрічає однакові (відповідні) точки фігури. “Ідеальним” прикладом такої фігури є куля, центр якого і є його центром симетрії.

Геометрична фігура симетрична, якщо існують перетворення, при яких її точки змінюють своє розташування на площині або в просторі, однак фігура накладається сама на себе. Якщо частини такої фігури накладаються на інші частини, то ці частини називають симетричними між собою. В залежності від типу перетворень розрізняють різні види симетрії.

 

 

 

 

Дзеркальна симетрія

Рис.3

Дзеркальною називається симетрія відносно  площини або, в планіметрії, лінії.  У планіметрії цей тип симетрії називають осьовою (рис.3).

Симетрія обертання

Симетрією обертання називається симетрія щодо повороту на певний кут відносно певної лінії, яка називається віссю обертання. Якщо фігура симетрична щодо повороту на будь-який кут, її називають аксіально-симетричною. Прикладом аксіально-симетричної фігури є коло, а в тривимірному просторі циліндр обертання.

Якщо фігура симетрична відносно повороту тільки на певні кути, то ці величини цих кутів визначаються формулою , де N ціле число, оскільки при повороті на кут  фігура завжди накладається сама на себе. Відповідні осі обертання називають осями симетрії N-го порядку.

Центральна симетрія

Рис.4

Геометрична фігура має центральну симетрію відносно певної точки, яка називається центром симетрії, якщо для будь-якої точки фігури існує інша точка, розташована на лінії, що сполучає дану точку з центром, з іншого боку від центра на однаковій відстані(рис.4).

Трансляційна симетрія

Трансляційною симетрією називають симетрію щодо паралельного переносу у певному напрямку на певну відстань. Трансляційну симетрію мають ґратки. Граничним випадком трансляційної симетрії є однорідність простору. Однорідний простір накладається сам на себе при довільному зміщенні.

Осьова симетрія

Осьова симетрія - тип симетрії, що має два дещо відмінні визначення:

•                   Відбивна симетрія. У математиці (точніше, евклідовій геометрії) осьова симетрія - вид руху ( дзеркального відображення), при якому безліччю нерухомих точок є пряма, яка називається віссю симетрії. Наприклад, плоска фігура прямокутник в просторі осесиметрична і має 3 осі симетрії (дві - в площині фігури), якщо це не квадрат.
•                   Обертальна симетрія. У природничих науках під осьовою симетрією розуміють обертальну симетрію (інші терміни - радіальна, аксіальна, променева симетрії) щодо поворотів навколо прямої. При цьому тіло (фігуру, завдання, організм) називають осесиметричними, якщо вони переходять в себе при будь-якому (наприклад, малому) повороті навколо цієї прямої. У цьому випадку, прямокутник не буде осесиметричним тілом, але конус буде.

Стосовно до площини ці обидва види симетрії збігаються (вважаємо, що вісь теж належить цій площині).

Іноді вводять також (осьову) симетрію деякого порядку:

•                   Осьова симетрія n-го порядку - симетричність щодо поворотів на кут 360º/ n навколо будь-якої осі. Описується групою Z n.
•                   Тоді симетрія в першому сенсі (див. вище) є осьовою симетрією другого порядку.
•                   Вісь симетрії ∞-го порядку - поворот на будь-який кут призводить до поєднання з самим собою. Наприклад: коло, куля.
•                   Осі симетрії 2-го, 3-го, 4-го, 6-го і навіть 5-го порядку (кристали з неперіодичних просторовим розташуванням атомів) можна спостерігати на прикладі кристалів.
•                   Дзеркально поворотна осьова симетрія n-го порядку - поворот на 360 / n і відображення в площині, перпендикулярній даної осі.

Осі симетрії L3, L4, L6 називаються осями симетрії вищого порядку

1.2 Зв'язок між поняттями симетрії та асиметрії 

Про визначення категорій симетрії та асиметрії.

В даний час в науці переважають визначення зазначених категорій на основі перерахування їх найважливіших ознак. Наприклад, симетрія визначається як сукупність властивостей: порядку, однорідності, відповідності, пропорційності, гармонійності і т. д. Асиметрія ж зазвичай визначається як відсутність ознак симетрії, як безлад, нерозмірність,неоднорідність і т. д.

 Всі ознаки симетрії в такого роду її визначеннях, природно, розглядаються як рівноправні, однаково істотні, і в окремих конкретних випадках при встановленні симетрії якогось явища можна користуватися будь-яким з них. Так, в одних випадках симетрія - це однорідність, а в інших - відповідність і т. д. Очевидно, що в міру розвитку нашого пізнання до визначення симетрії можна додавати все нові і нові ознаки. Тому визначення симетрії такого роду завжди неповні.

Те саме можна сказати і про існуючі визначення асиметрії. Очевидно,що у визначеннях понять, сформульованих за принципом перерахування властивостей об'єктів, що ними відображаються, відсутній зв'язок між перерахованими властивостями об'єктів.

Такі властивості симетрії, як, наприклад , однорідність і відповідність, один з одного не дотримуються. Сказане, однак, не означає непотрібності вищевказаних визначень симетрії та асиметрії. Навпаки, вони вельми корисні й необхідні. Без них не можна дати і більш загальне визначення категорій симетрії та асиметрії. «У симетрії, - пише А. В. Шубников, - відбивається та сторона явищ, яка відповідає спокою, а в дісіметрії (за нашою термінології в асиметрії) та їх сторона, яка відповідає руху »

Таким чином, всі властивості симетрії розглядаються як прояви станів спокою, а всі властивості асиметрії – як прояви станів руху. Якщо визнати, що це правильно, то очевидно, що співвідношення симетрії та асиметрії в такому випадку таке ж, як співвідношення спокою і руху. Ми, отже,можемо сказати, що симетрія відносна, а асиметрія абсолютна. Симетрію ми повинні, далі, розглядати як окремий випадок асиметрії, як її момент. Тому ні про яку рівноправність симетрії і асиметрії і мови бути не може. Взаємовідносини симетрії і асиметрії тут явно асиметричні. Але навряд чи можна з таких позицій правильно зрозуміти багато властивостей симетрії та асиметрії. Чому, наприклад, таку симетрію простору, як його однорідність, повинні розглядати як відповідну спокою? Чому ми повинні шукати симетрію тільки серед явищ, що покояться? Хіба немає симетрії у взаємодії та русі явищ світу? 
     Думка про зв'язок між поняттями симетрії та асиметрії і відповідно між поняттями спокою і руху точніше можна виразити як єдність спокою і руху. Поняття симетрії розкриває момент спокою, рівноваги в станах руху, а поняття асиметрії - момент руху, зміни до стану спокою, рівноваги. Але і таким формулюванням не охоплюють основні ознаки симетрії і асиметрії. Наприклад, симетрія частинок і античастинок та їх асиметрія відомої нам області світу не можуть бути витлумачені виходячи з понять про єдність спокою і руху. Навряд чи існування частинок і античастинок можна розглядати як момент спокою в якомусь русі матерії, а невідповідність числа частинок числа античастинок у відомій нам області світу як моменти руху в якомусь стані спокою. Можна зробити висновок, що в ідеї А. В. Шубнікова про співвіднесенні симетрії з спокоєм, а асиметрії – з рухом полягає тільки момент істини.

Добре відомо, що поняття симетрії охоплює і такі сторони існування явищ, які нічого спільного з спокоєм не мають. Наприклад,регулярна повторюваність тих чи інших станів руху, їх певна періодичність є однією з ознак симетрії, але до спокою, вона ніякого відношення не має.

До загальних визначень понять симетрії та асиметрії можна підійти виходячи з наступних положень: по-перше, потрібно визнати, що ці поняття відносяться до всіх відомих нам атрибутів матерії, що вони відображають взаємні зв'язки між ними, по-друге, ці поняття ґрунтуються на діалектиці співвідношення тотожності і відмінності, що існує як між атрибутами матерії, так і між їхніми станами та ознаками; по-третє, потрібно мати на увазі, що єдність симетрії і асиметрії являє собою одну з форм прояву закону єдності і взаємно виключення протилежності. Правильність цих відправних положень може бути доведена як виведенням їх з численних приватних визначень симетрії і асиметрії, так і правильністю їх наслідків, тобто необхідністю і загальністю визначень симетрії і асиметрії,отриманих на їх основі. 
        Безпосередньою логічною основою для визначення понять симетрії і асиметрії, на наш погляд, є діалектика тотожності і відмінності. Тут потрібно відзначити, що в діалектиці тотожність і відмінність розглядаються лише у визначених відносинах, у взаємодії, у включенні відмінності в тотожність, а тотожності в розходження. 
Ідентичність виявляється тільки в певних відносинах і в певних процесах; тотожність завжди конкретна. До тотожності можна віднести:рівновагу,   збереження, стійкість, рівність, співмірність, повторюваність і т. д. Тотожність не існує вічно: вона виникає, стає і розвивається. Якщо дати їй загальне визначення, то можна сказати, що воно являє собою процес утворення схожості в різному. 
        Для того, щоб мала місце тотожність, необхідне існування різноманітного і протилежного.

Характеризуючи діалектичне розуміння тотожності, потрібно виділити його наступні сторони: тотожність не існує поза відмінності і протилежності, тотожність виникає і зникає; тотожність існує тільки у визначених відносинах і виникає за певних умов, найбільш повним вираженням тотожності є повне перетворення протилежностей одна в одну. Прояви тотожності нескінченно різноманітні. Тому в процесі пізнання явищ світу не можна обмежуватися лише встановленням тотожності між ними, але необхідно розкривати те, як виникає ця тотожність, за яких умов і в яких відносинах воно існує. Ґрунтуючись на цій характеристиці діалектики тотожності і відмінності, можна сформулювати такі визначення симетрії та асиметрії.

        Вже з означень симетрії та асиметрії випливає їх нерозривна єдність. 
Ця обставина певною мірою підкреслена А. В. Шубниковим: «Якого б трактування симетрії ми не дотримувалися, одне залишається обов'язковим: не можна розглядати симетрію без її антипода - асиметрії».

У всіх реальних явищах симетрія і асиметрія поєднуються одна з одною. І треба думати, що у всіх правильних, тобто відповідних дійсності, наукових узагальненнях мають місце не просто ті чи інші симетрії або асиметрії, а певні форми їх єдності. 

Вивчення об'єктивної реальності і завдання практики призвели до виникнення поряд з поняттям симетрія і поняття асиметрії, яке знайшло одне зі своїх перших кількісних виразів в  золотому розподілі, або золотій пропорції.

Піфагор висловив «золотою пропорцію» співвідношення:

А: Н = R: B, 

 де Н і R  гармонійні і арифметичні середні між величинами А і В.

R = (A + B)/2; H = 2AB/(A + B).

Кеплер перший звертає увагу  на значення цієї пропорції в ботаніці і називає її sectio divina - «божественний перетин»; Леонардо да Вінчі називає цю пропорцію «золотий перетин». 

Пропорція «золотого перетину» дає можливість архітекторам знаходити найбільш вдалі, красиві, гармонійні перетину цілого і частин, єдність різноманітного;  взагалі вони користуються поєднанням принципів симетрії і асиметрії. 
         Якщо в період Відродження увага вчених і викладачів мистецтва була прикута до «золотого перетину», то згодом вона поступово падала, і лише в 1855 р. німецький вчений Цейзинга знову ввів його в побут у своїй праці «Естетичні дослідження». У ньому він писав, що для того, щоб ціле, розділене на дві нерівні частини, здавалося прекрасним з точки зору форми, між меншою і більшою частинами повинно бути те ж відношення, що й між більшою частиною і цілим. 
Застосування «золотого перетину» є лише окремий випадок загального закону періодичної повторюваності одній і тій же пропорції в сукупності, в деталях цілого, 
Розгляд питання про «золотому перетині» приводить до висновку, що тут ми маємо справу з відображенням засобами математики (за допомогою понять симетрії та асиметрії) існуючої в природі пропорційності.

РОЗДІЛ 2.

СИМЕТРІЯ ТА АСИМЕТРІЯ НАВКРУГ НАС

2.1  «Золотий переріз» у гармонії  життя

 Історія золотого перерізу цікава і захоплю­юча. Вона ще раз підтверджує, що таємниці природи заховані і ревно нею оберігаються. Таємниця золотого перерізу — не виняток.

 Вважають, що поняття золотого перерізу ввів Піфагор та його учні (VI ст. до н.е.). При­пускають, що Піфагор свої знання про золотий переріз запозичив у єгиптян та вавілонян.

 І справді, пропорції піраміди Хеопса, храмів, барельєфів, предметів побуту і прикрас із гробниці Тутанхамона свідчать, що єги­петські майстри користувалися співвідношен­ням золотого перерізу під час їх створення.

 Аналіз грецьких статуй показує, що в осно­ву їх створення також покладено золотий пе­реріз.

 Майстри Стародавньої Греції вміло корис­тувалися золотою пропорцією, використовува­ли її гармонічні величини в усіх видах мистец­тва і досягли такої досконалості побудови  форм, яка рідко зуст­річається у практиці світового мистецтва.

 Уся антична куль­тура побудована за за­конами золотої про­порції.

 Історія вчення про пропорції — це істо­рія   пошуків  теорії гармонії та краси. Уся антична естетика, а також естетика епохи Відродження базуєтьcя на законах краси і співрозмірності окре­мих частин і цілого. Цю пропорційність форм. дають золотий переріз і симетрія.

 В епоху Відродження посилюється інтерес до золотого перерізу серед учених і худож­ників у зв'язку з його застосуванням як у гео­метрії, так і в мистецтві, особливо в архітектурі.

 У 1509 р. у Венеції вийшла книга Луки Пачолі (1454—1514) «Божественна пропорція»,  де чудові ілюстрації зробив друг Пачолі — Леонардо да Вінчі.

 Сам термін «золотий переріз» увів Леонар­до да Вінчі.

 Золотий переріз — гармонічна пропорція.

 Видатні майстри живопису Леонардо да Вінчі, Фідій, Тіціан, Рафаель та інші в основу своїх безсмертних творінь поклали золоту про­порцію або золотий переріз.

 Й. Кеплер говорив, що геометрія володіє двома скарбами — теоремою Піфагора та золо­тим перерізом, і якщо перший з цих скарбів можна порівняти з мірою золота, то другий з дорогоцінним каменем — діамантом.

Походження золотого перерізу

 Поняття золотого перерізу ввів Піфагор – давньогрецький філософ і математик (VI ст.. до н.е.). є припущення, що Піфагор знання про нього запозичив у єгиптян і вавилонян. І справді, пропорції піраміди Хеопса, храмів, барельєфів, предметів побуту та прикрас з гробниці Тутанхамона свідчать, що єгипетські майстри користувалися співвідношеннями золотого перерізу  під час їх створення. Французький архітектор Ле Корбюзьє знайшов, що в рельєфі з храму фараона Сеті в Абідосі та рельєфі, що зображає фараона Рамзеса, пропорції фігур відповідають золотому пере­різу. Архітектор Хесира, зображений на рельєфі дерев'яної дошки з гробниці його імені, тримає в руках вимірювальні інструменти, де зафіксо­вано пропорції золотого перерізу.

 Платон (427—347 рр. до н.е.) також знав про золотий переріз і приділяв увагу математичним і естетичним переконанням школи Піфагора, зокрема питанням золотого перерізу. 

У фасаді давньогрецького храму Парфенону є золоті пропорції. Під час його розкопок ви­явлено циркулі, якими користувалися архітек­тори та скульптори античного світу.

 У Помпейському циркулі (музей у Неаполі) також закладено пропорції золотого поділу.

 В античній літературі, що дійшла до нас, золотий переріз уперше згадується в «Началах» Евкліда. У 2-й книзі «Начал» дається геомет­рична побудова золотого перерізу. Після Евк­ліда дослідженням золотого перерізу займали­ся Гіпсікл (бл. 180 р. до н.е.), Папп (III ст. н.е.) та інші. У середньовічній Європі із золотим перерізом ознайомилися за арабськими пере­кладами «Начал» Евкліда. Італійський матема­тик і перекладач Дж. Кампано (XIII ст.) зробив новий переклад «Начал» і дав до перекладу цінні коментарі та доповнення. Способи золо­того перерізу зберігалися у великій таємниці. Вони були відомі тільки окремим ученим.

 В епоху Відродження посилюється інтерес до золотого перерізу серед учених і художників у зв'язку з його застосуванням як у геометрії, так і в мистецтві, особливо в архітектурі. Леонардо да Вінчі, художник і вчений, бачив, що в іта­лійських художників емпіричний досвід вели­кий, а знань мало. Він почав писати книгу з геометрії, але в цей час з'явилася книга ченця Луки Пачолі (1454-1514), і Леонардо залишив свій задум. На думку сучасників і істориків, Лука Па­чолі був справжнім світилом, найбільшим мате­матиком Італії в період між Фібоначчі і Галілеєм. Лука Пачолі був учнем художника П'єро Делла Франческі, що написав дві книги, одна з яких «Про перспективу в живописі». Його вва­жають творцем нарисної геометрії.

Лука Пачолі чудово розумів значення науки для мистецтва. У 1496 р. на запрошення гер­цога Моро він приїжджає до Мілана, де читає лекції з математики. У Мілані при дворі гер­цога у той час працював і Леонардо да Вінчі. У Венеції була видана книга Луки Пачолі «Боже­ственна пропорція» з блискуче виконаними ілюстраціями, зважаючи на що вважають, що їх зробив Леонардо да Вінчі. Книга була захоп­леним гімном золотої пропорції. Серед бага­тьох переваг золотої пропорції чернець Лука Пачолі не забув назвати і її «божественну суть» як вираз божественної триєдиності (розумію­чи, що малий відрізок є уособлення Бога Сина, більший відрізок — Бога Батька, а весь відрізок — Бога Духу Святого).

 Леонардо да Вінчі також багато уваги при­діляв вивченню золотого перерізу. Він прово­див перерізи стереометричного тіла, утворено­го правильними п'ятикутниками, і кожного разу отримував прямокутники з відношеннями сторін у золотій пропорції. Тому він дав цьо­му діленню назву золотий переріз. Така назва найпопулярніша і донині.

 У подальші століття правило золотої про­порції перетворилося на академічний канон. У 1855 р. німецький дослідник золотого перерізу професор Цейзінг опублікував свою працю «Ес­тетичні дослідження». Він абсолютизував про­порцію золотого перерізу, оголосивши її універ­сальною для всіх явищ природи та мистецтва.

Означення золотого перерізу

 Людина розрізняє предмети,що її оточують за формою. Інтерес до форми якого-небудь пред­мета може бути викликаний життєвою необхід­ністю або — красою форми. Форма, в основі побудови якої лежить поєднання симетрії та золотого перерізу, сприяє якнайкращому зоро­вому сприйняттю і появі відчуття краси й гар­монії. Ціле завжди складається з частин, час­тини різної величини знаходяться в певному відношенні один до одного і до цілого. Прин­цип золотого перерізу — це найвищий прояв структурної та функціональної досконалості цілого і його частин у мистецтві, науці, техніці та природі.

 Золотий переріз — це гармонійна пропорція.

 У математиці пропорцією називають рівність двох відношень.

 Відрізок прямої АВ можна розділити точ­кою С на дві частини такими двома способа­ми:

1) на дві рівні частини АВ : АС — АВ: ВС;

2) на дві нерівні частини в будь-якому відношенні (такі частини пропорції не утворю­ють);

 Якщо АВ : АС = АС : ВС, то такий поділ відрізка буде золотим перерізом або діленням відрізка в крайньому та середньому відно­шенні.

 Означення. Золотий переріз — це такий поділ цілого на дві нерівні частини, при яко­му більша частина так відноситься до цілого, як менша — до більшої.

 Якщо довжину відрізка АВ позначити через а, а довжину відрізка АС через х, то довжина відрізка СВ буде  а — х.

Тоді за означенням     

                                      

 Звідси видно, що при золотому перерізі довжина більшого відрізка є середнім геомет­ричним або середнім пропорційним довжин всього відрізка і його меншої частини:

                                                   

 Геометрично золотий переріз відрізка АВ можна виконати так.

 З рівняння х² =а(а- х) маємо рівняння

                                     

звідки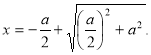                                  

 Відрізок х будуємо так. У точці В ставимо перпендикуляр до АВ і на ньому відкладаємо відрізок:   .   Тоді

                                      

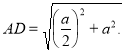
 Від АD  віднімемо ВD, тобто будуємо DЕ=DВ. Тоді АЕ = х. Відкладаємо АС = АЕ. Точка С ділить АВ у золотому перерізі.

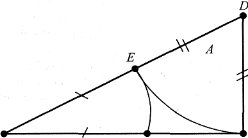
                                      А                                 С                      В

  Обчислимо значення х:

                                          

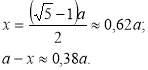
  Отже, частини золотого перерізу становлять приблизно 62% і 38% всього відрізка.

Золотий переріз  в геометрії

Теорему Піфагора знає кожен школяр, а що таке золота пропорція — далеко не всі.

  Згадаємо, Золотий переріз — це таке пропорційне ділення відрізка на нерівні частини, при яко­му весь відрізок так відноситься до більшої ча­стини, як більша частина відноситься до мен­шої; або менший відрізок так відноситься до більшого, як більший до всього:

                             a: b= b: c  або  c: b = b: a.

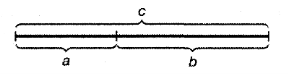
  Відрізки золотої пропорції  виражаються нескінченним ірраціональним дробом 0,618…Якщо у записаному відношенні с прийняти за одиницю, то а=0,382... Як ми вже знаємо, числа 0,618 і 0,382 є коефіцієнтами послідов­ності Фібоначчі.

 Прямокутник з таким відношенням сторін стали називати золотим прямокутником. Він також має цікаві властивості. Якщо від нього відрізати квадрат, то залишиться знову золо­тий прямокутник. Цей процес можна продов­жувати до безмежності. А якщо проводити діа­гоналі попереднього і наступного прямокутни­ка, то точка їх перетину належатиме всім от­римуваним золотим прямокутникам.

 Німецький фізик і психолог Густав Фехнер, один із основоположників експериментальної психології, дослідив, що людині подобається більше той прямо­кутник, сторони якого знаходяться у відношенні зо­лотого перерізу.

 Тому нам більше подобаються і здаються прекрас­ними ті речі, які відповідають золотому перерізу.

 Є і золотий трикутник. Це рівнобедрений трикутник, у якого відношення довжини бічної сторони до довжини основи дорівнює 1,618.

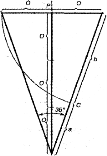
 У зірчастому п'я­тикутнику кожна з п'яти ліній, що утво­рюють фігуру, ділить іншу у відношенні золо­того перерізу, а кінці зірки є золотими трикут­никами.

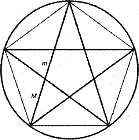
 Піфагор вважав правильний п'ятикутник незви­чайною фігурою і дарував його зображення тільки друзям як символ дружби. Діагоналі п'ятикутника утворюють правильну зірку, яку піфагорійці сприй­мали як символ здоров'я.

 Для побудови такої правильної зірки піфагорійці користувалися тим, що кожна з п'яти діагоналей пра­вильного п'ятикутника ділить іншу у відношенні зо­лотого перерізу.

 Правильність цього відношення випливає з по­дібності трикутників.

 Усередині п'ятикутника знаходиться зірка, усе­редині зірки — п'ятикутник, у ньому — знову зірка і т.д.

 На перший погляд золотий переріз відрізка ви­дається дуже складним і рідкісним. Але це не так, оскільки він існує у природі, а уважні люди його по­мітили.

Природничі основи золотого перерізу

 Золотий переріз був відомий і до Піфагора, ще в стародавньому Вавилоні. Таке правило поділу вига­дали не люди, а створила сама природа.

 Німецький поет і філософ Адольф Цейзинг час­тину свого життя присвятив вивченню золотого пе­рерізу. У 1855 р. надруковано працю «Естетичні до­слідження», у якій він стверджує, що в природі існує порядок і виражається він у відношенні золотого перерізу. А. Цейзинг провів дослідження кількох ти­сяч людських тіл. І виявив, що в середньому талія дорослого чоловіка ділить його тіло у відношенні золотого перерізу.

 Він встановив, що для чоловіка відношення зро­сту до довжини торсу становить            а для жінки        

 Отже, пропорція чоловічої фігури ближча до зо­лотого перерізу, ніж жіночої. Філософ вважав, що для того, аби ціле, поділене на дві нерівні частини, здавалося прекрасним щодо форми, між меншою і більшою його частинами має бути таке саме відно­шення, як і між більшою і цілим.

 Ділення тіла точкою пупа — най­важливіший показник золотого перерізу. Про­порції чоловічого тіла коливаються в межах се­реднього відношення 13 : 8 = 1,625 і ближче підходять до золотого перерізу, ніж пропорції жіночого тіла, для якого середнє значення про­порції виражається співвідношенням 8:5 = 1,6. У новонародженого таке відношення становить 1: 1, до 13 років воно дорівнює 1,6, а до 21 року дорівнює, залежно від статі, чоловічому або жіночому. Пропорції золотого перерізу виявля­ються і щодо інших частин тіла: довжина пле­ча, передпліччя і кисті, кисті і пальців і т.д.

 Свою теорію пропорцій людського тіла детально розробив Альберт Дюрер. Він дослідив, що зріст людини ділиться в золотих пропорціях лінією талії, а також лінією, проведеною через кінчики середніх пальців опущених рук, нижня частина обличчя – ротом і т.д.

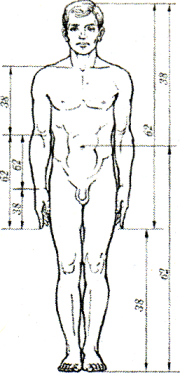
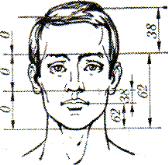 На малюнках показано золоті пропорції людини по всій фігурі і по частинах тіла.

 

           

 

 

 

 

 

 

 

                            

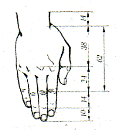
 Людина — найдосконаліше творіння приро­ди — створена в пропорції золотого перерізу, які ми спостерігаємо в будові тіла, рук, кисті, ока.

 За законами золотого перерізу природа поді­лила добу на дві частини: для сну людини — 9 год 7 хв, для всього іншого — 14 год 53 хв.

 Пізніше вчені дослідили, що вся жива та не­жива природа створена за законами золотого перерізу. Після утворення Землі жива приро­да розвивалась або вгору, або розстелялась по землі, або закручувалась по спіралі за закона­ми золотого перерізу.

 Розглянемо, як росте рослина цикорій(рис.5). Біля основи утворюється листочок, далі паросток росте вгору (робить викид у простір, зупи­няється, випускає листочок меншого розміру, знову робить викид, але менший за попе­редній, і знов випускає листочок і т.д.). Якщо довжину першого викиду взяти за 100 оди­ниць, то другий буде дорівнювати 62, третій - 38, четвертий - 24, п'ятий - 4. Довжина пелюсток теж підпорядкована золотій пропорції. Зростаючи, завойовуючи простір, рослина зберігає певні пропорції. Імпульси її зростання поступово зменшуються в пропорції золотого перерізу.

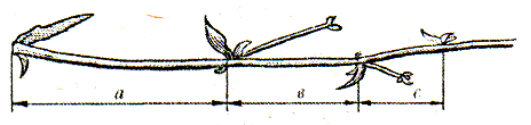
Рис.5

 Іншим прикладом може бути ящірка(рис.6).

 На її тілі видно з першого погляду такі пропорції: довжина її хвоста відноситься до довжини тулуба як 62 : 38.

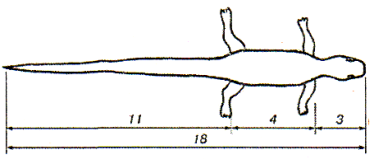
Рис.6

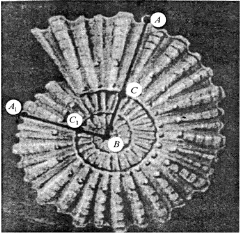 Розглянемо мушлю(рис.7).

 

 

                                                      Рис.7

На ній точки С і С1   ділять відповідно відрізки АВ і  А1В у відношенні золотого перерізу (на першому і другому витках).

 І у рослинному, і в тваринному світі наполегливо проявляється формоутворювальна тенденція природи – симетрія щодо напрямку зростання та руху. Тут золотий переріз виявляється в пропорціях частин перпендикулярно до напряму зростання.

 Природа здійснила поділ на симетричні частини та золоті пропорції.

Золотий переріз у мистецтві та живописі

 Cеред нескінченних форм у при­роді панує закономірність і системність, що пов'язані пропорціями золотого перерізу. Природа — великий учитель, а художник — учень приро­ди. Тому художник повинен не тільки малюва­ти з натури і копіювати природу, а й вивчати композиційні закони природи, закони формо­утворення, творити за законами природи, го­ворити мовою природи і створювати картини за законами гармонії та краси. Нам приємно дивитися на твори мистецтва, у яких дотрима­но пропорції золотого перерізу. Вони викли­кають естетичні почуття.

 Портрет Мони Лізи (Джоконди)(рис.8), створений геніальним Леонардо да Вінчі, показує, що композиція малюнка побудована на золотих трикутниках (трикутники, що є частинами правильного зірчастого трикутника).

 

Рис. 8 Леонардо да Вінчі. Портрет Мони Лізи

 Аналіз картин видатних художників І. Рєпіна, В. Сурикова, О. Іванова, Г. Федотова та багатьох інших свідчить, яке велике значення має золотий переріз у створенні композиції картини.

 Використання золотого перерізу прослідковується у величних полотнах Рафаеля «Заручи­ни Марії», О. Іванова «З'явлення Христа народу»(рис. 9), В. Сурикова «Бояриня Морозова»(рис.10), «Ранок стрілецької страти»(рис.11), Т. Яблонської «Хліб»,    А. Рубльова «Трійця».

                           

Рис. 9 О.Іванов. З’явлення Христа народу

                                                                           Рис.10  Василь Суриков. Боярина Морозова                                                                           

                                                        Рис.11 Василь Суриков. Ранок стрілецької страти

                                                   Рис. 12      Ілля Рєпін. О.С.Пушкін на акті в ліцеї 8 січня 1815р.

 Фігура О. Пушкіна в картині І. Рєпіна «О.С. Пушкін на акті в ліцеї 8 січня 1815 року» (рис.12) розміщена на лінії золотого перерізу в правій частині картини; ліва частина картини, у свою чергу, теж поділена в пропорції золотого перерізу, від голови Пушкіна до голови Державіна і від неї до лівого краю картини.

 Повторення рівних величин, чергування рівних і нерівних величин у пропорціях золотого перерізу створює в картині певний ритмічний ряд, який викликає у глядача той чи інший настрій.

 Для кращого сприймання картини центр уваги повинен бути або в лівому або в правому боці картини, вгорі або внизу. Ці чотири точки — найкращі для розміщення головного предмета чи особи картини, і ці точки повинні зна­ходитися на перетині ліній золотого перерізу.

 Золотий переріз не можна розглядати окремо, без зв'язку із симетрією як одним з важливих факторів краси форм. Нині в науку ввійшли поняття статичної та динамічної симетрії. Золотий переріз називають динамічною симетрією, у якій, на відміну від статичної, відрізки не залишаються рівними, а збільшуються або зменшуються у величинах золотого перерізу зростаючого або спадного ряду.

 Художня форма, в основу побудови якої покладено пропорції золотого перерізу, і особливо поєднання симетрії і золотого перерізу, є високоорганізованою формою, що сприяє яскравішому висловленню змісту, найлегшому зоровому сприйманню, і завдяки цьому у глядача з'являється відчуття краси.

 Дуже часто в одних і тих самих творах живопису зустрічаються поєднання симетричного поділу на рівні частини по вертикалі та поділу на нерівні частини золотого перерізу по горизонталі. Картина Леонардо да Вінчі «Мадонна в гроті»(рис.14) не строго симетрична, але в основі її побудови — симетрія. Усі пропорції в картині є похідними від висоти, утворюють ряд відношень золотого перерізу і служать основою гармонії форм і ритму, що несуть у собі заряд емоційного впливу.             

 

   

 

 

 

 

 

 

 

                                  Рис.14   Леонардо да Вінчі. Мадонна в гроті

 Великий майстер Антоніо Страдіварі використовував співвідношення золотого перерізу у своїх знаменитих скрипках(рис.15).

Рис. 15

 Відомий кінорежисер С. Ейзенштейн наводив приклади золотого перерізу в поезії та детально описав побудову за законами золотого перерізу свого фільму «Броненосець Потьомкін».

 Не можна не згадати про Т. Шевченка. Розглянемо одну з його робіт. У художній академії в Петербурзі він навчався анатомії, рисунку, перспективи та композиції у своїх учителів — І. Сошенка, К. Брюлова та ін., які наслідували кращі традиції мистецтва Греції, і став великим художником.

 За картину «Циганка-ворожка» (рис.16) у 1841 р. його нагороджено срібною медаллю.

У цій картині фігури ворожки і дівчини розміщені по вертикальних лініях зо­лотого перерізу, а руки — на діагоналі.

 По горизонталі (розміщення голів ворожки., дівчини та дитини) теж прослідковується використання золотого перерізу.

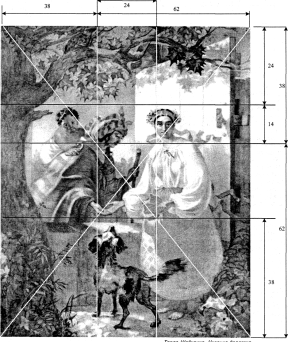
                                                          Рис. 16 Тарас Шевченко. Циганка – ворожка

 

 

 

 

 

Поділ полотна картини

 Для того щоб геометричне поділити картину, спочатку вимірюють довжину картини і половину довжини картини відкладають на ширину картини. Одержану точку С сполучають з лівим нижнім кутом картини.

 Будують відрізок СD = ВС на відрізку AC від точки С.  Одержують відрізок АD, що відкладають на відрізку АВ від точки А. Одержана точка Е ділить відрізок АВ у золотому перерізі 62 : 38.

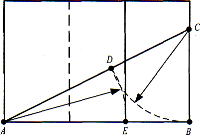
 Щоб знайти лінії золотого перерізу по горизонталі, ділять довжину картини справа наліво і зліва направо в золотому поділі 62 : 38. Висоту картини розділити в золотому перерізі легко, провівши діагоналі пря­мокутника.

 Ці лінії знадобляться при побудові пейзажу.

Побудова ескізу пейзажу

 Художники-пейзажисти з досвіду знають, що не можна відводити половину площини малюнка під небо або під землю і воду. Краще брати або більше неба, або більше землі, тоді пейзаж «краще дивиться».

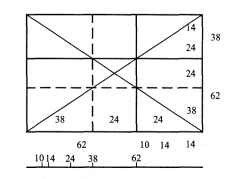
 Якщо продовжити далі пропорційний поділ довжини і висоти картини, то одержимо відрізки спадного ряду золотої пропорції 100, 62, 38, 24, 14, 10.

 Перенесемо ці відрізки на картину. Нехай картина вже поділена по вертикалі лінією золотого перерізу. Перенесемо цю лінію в лівий бік картини. Відстань між лініями золотого перерізу в середині картини дорівнює 24 частинам. Відрізок, що дорівнює 24 частинам, накладаємо на відрізок, який дорівнює 38 частинам (38 - 24 = 14), одержимо різницю, що дорівнює 14 частинам. Останній відрізок накладаємо на відрізок, що дорівнює 24 частинам   (24 - 14=10), і одержуємо відрізок, що дорівнює 10 частинам. Усі відрізки спадного ряду золотої пропорції для даної картини ми отримали. Такий самий поділ виконуємо по висоті картини.

 Одержані відрізки переносимо на смужки для ширини і висоти картини. Цей інструмент назвемо пропорційною лінійкою. Але ця лінійка підходить лише для ескізу даного розміру, її виготовлення для іншої картини забере кілька хвилин, але в майбутньому зробить легкою роботу над ескізом під час з'ясування відстаней між фігурами або групами фігур, між предметами, допоможе знайти їх розміри і, зрештою, гармонічно здійснити лінійну побу­дову картини.

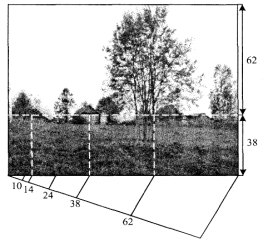 Для побудови ескізу  пейзажу на заданому фор­маті необхідно поділити аркуш паперу з допомогою про­порційної лінійки. Користуючись етюдами, підготовленими заздалегідь,  необхідно розмістити на лінії золотого перерізу найгарніші предмети, які привертають увагу глядача, наприклад дерево. Усі інші предмети доповнюють пейзаж і повинні бути розміщені по лініях гармонічного ряду. Лінію горизонту також розмістити вздовж горизонтальної лінії золотого перерізу. Така побудова пейзажу легко сприймається очима(рис. 17).

 

 

 

 

 

 

Рис. 17

 Усю іншу роботу над пейзажем потрібно виконувати так, як підказують відчуття, але дотримуючись законів композиції та правил зображень, які вивчали. Картину поділено в кількісному відношенні. Далі ці відношення мають втіли­тися в живі форми листя, дерев, квітів, тварин, у світлові тони, що дадуть естетичне задово­лення та відчуття краси.

 

Золотий переріз в архітектурі

 Тільки дотримуючись законів геометрії, архітек­тори змогли створити свої шедеври. Пропорція в архітектурі — це ніби її внутрішня краса. Вона невидима безпосередньо, але завжди відчутна, як і краса духовна. Особливо велику роль відіграє золотий пе­реріз в архітектурі. Розглянемо фасад одного з найкращих витворів давньогрецьких архітекторів — храм богині Афіни, побудований у V ст. до н.е. в Афінах(рис.18).

Рис. 18

 Відношення висоти цієї будівлі до її довжини ста­новить 0,618.

Архітектором Філіппо Брунеллескі у XV ст. на основі золотого перерізу створена капела Пацці у Флоренції(рис.19).

Рис. 19

 Золотий переріз використано під час побудови ба­гатьох споруд з колонами, фрагментів архітектури у Києві, Санкт-Петербурзі, Москві.

  Золотий переріз є домінуючим у скульптурі. Роз­глянемо статую Аполлона, яку вважають еталоном чо­ловічої краси. Якщо її висоту поділити у відношенні золотого перерізу і це саме проробити з кожною час­тиною тіла, то точки поділу припадуть на анатомічне важливі місця: початок шиї, талію, коліно. Така сама закономірність поширюється на руки та обличчя.

  Піраміди. Багато хто намагався розгадати таємниці Великої піраміди в Гізі. На відміну від інших єгипетських пірамід, це не гробниця. Ви­нахідливість і майстерність архітекторів, вико­ристані ними пропорції, символи указують на надзвичайну важливість послання, яке вони хотіли передати майбутнім поко­лінням через збудовану піраміду.

 Ключ до геометрично-математичної таємниці Великої піраміди в Гізі, що так довго був для людства загадкою, на­справді був переданий Геродоту храмовими жерцями, які повідомили, що піраміда побу­дована так, щоб площа кожної із її граней до­рівнювала квадрату її висоти.

Інтенсивні дослідження Великої піраміди в Гізі показали, наскільки обширними були в ті часи пізнання в математиці й астрології. У всіх внутрішніх і зовнішніх пропорціях піраміди число 1,618 грає центральну роль.

  Не тільки єгипетські піраміди побудовані відповідно до досконалих пропорцій золотого перерізу. Те саме явище виявлене й у мекси­канських пірамід. Виникає думка, що як єги­петські, так і мексиканські піраміди були зве­дені приблизно в один і той самий час.

  На перерізі піраміди можна побачити фор­му, подібну до сходів. У першому ярусі їх 16, у другому  - 42, у третьому  - 68.

  Ці числа пов'язані з послідовністю Фібо­наччі так:

16 · 1,618  26;  16 + 26 = 42;  26 · 1,618 42;  42 + 26 = 68.

Ритми серця й мозку

Серце б'ється безупинно – від народження людини до її смерті. Його робота має бути оптимальної, зумовленої законами самоорганізації біологічних систем. Відхилення від оптимального режиму викликають різні захворювання. Оскільки золота пропорція одна із критеріїв самоорганізації на живу природі, природно припустити, що у роботі серця можливо прояв цього критерію. Потрібні були глибокі дослідження, і вони було проведено радянським ученим В.Д. Цвєтковим.

Працюючи серця виникає електричний струм, що можна вловити спеціальним приладдям і отримати криву – електрокардіограму (ЕКГ) з характерними зубцями, що відбивають різні цикли роботи серця. В.Цвєтков встановив, що в людини й інших ссавців є оптимальна («золота») частота серцебиття, коли він тривалості систоли, діастоли і сповненого серцевого циклу співвідносяться між собою у пропорції ,  тобто в повній відповідності до золотої пропорції.

Отже, робота серця щодо тимчасових циклів, зміни тиску крові й обсягів шлуночків оптимізовано за одним і  тим же принципом – за правилом золотої пропорції.

Мозок людини являє собою надзвичайно складну систему, що само настроюється, основним призначення якої є регуляція діяльності різних органів людського тіла, здійснення зв'язку людини з довкіллям. У складі мозку розрізняють сіру та білу речовини. Сіра речовина є скупчення нервових клітин, біла – нервових волокон, відростків цих клітин. Нервова клітина з відростком називається нейроном. Нейрони мозку утворюють різноманітні мережі, взаємодіючи з допомогою електричних сигналів.

Конфігурації нейронних мереж є коливальні електричні ланцюги. Різноманітним станам мозку відповідають електричні коливання з різними частотами.

Численні досліди засвідчили, що у мозку дорослої людини,  в різних його станах переважають електричні коливання певних частот. Зміна активації мозку відбувається не безупинно, а лише дискретно, стрибками від рівня до іншого. Кожному стану мозку відповідають специфічні хвилі електричних коливань.

Стану спокійного неспання відповідає найбільш стійкий . Це основний ритм електричних коливань мозку, він з'являється у дитячому  віці й поступово із віком збільшується. Найбільш повільні коливання із частотою, ритму,  характерно для стану глибокого сну.

 

 

 

 

2.2    Чи важливі симетрія і асиметрія в професії дизайнера

 Інтер`єр - поняття складне, яке володіє естетичною психофізіологічною силою на людину.

 Дизайн - це творча діяльність, метою якої є формування гармонічного, предметного середовища для задоволення матеріальних і духовних потреб людини.

В житті людини є два протилежні бажання - прагнення отримати нових вражень і комфорту. Нові враження отримують, як правило, від подорожей, але не завжди вони асоціюються з комфортом. Скрасити незручність може одне - мрія про затишний готель.

Глибинно-просторова композиція складається з матеріальних елементів, об'єктів, поверхонь та простору, а також інтервалів між ними.

Одним із найважливіших засобів приведення різноманітних елементів форми до єдності, упорядкування їх розташування є ритм, який притаманний різноманітним явищам і формам природи, трудовим процесам і т.д.

Ритм - це рівномірне чергування розмірених елементів, порядок поєднання ліній, об'ємів, площин. Ритм діє на наші почуття. Ми сприймаємо не тільки оком, але й на слух. Ритм притаманний і статичним предметам. Наприклад, в архітектурних спорудах - ритмічний розподіл вікон по горизонталі і вертикалі. Ритм можна помітити і в площинному зображенні (орнамент).

Закономірне чергування об'ємів, граней, а також упорядкована зміна характерних елементів, форми - все це використовується в якості специфічного засобу композиції, як для окремих предметів і споруд, так і для комплексів.

Ритм може бути спокійний і не спокійний, може бути направлений в одну сторону, або збігатися до центру, направлений як по горизонталі так і по вертикалі.

Бажане враження від предмета можна досягти правильним використанням всіх можливостей ритму, продуманим чергуванням елементів, об'ємів, кольорових плям, як би направляючих рухатись око в співвідношенні з вибраним ритмом.

Широко використовується кольоровий ритм. Кольоровий ритм створює своєрідний кольоровий ритм.

Ми не можемо зорово сприймати виріб закінченим, якщо його маси конструктивно не врівноважені. Воно повинно бути не тільки фізично, а й зорово стійким. Отже, важливе місце в композиції займає рівновага.

Рівновага - це такий стан форми, при якому всі елементи збалансовані між собою. Вона залежить від розподілу мас композиції відносно її центру. Рівновага, як і ритм притаманна рослинному і тваринному світу. Рівновага об'ємів, або частин любого предмета викликає почуття спокою, упевненості і стійкості.

Динаміка - це зорове сприймання руху, стрімкості, форми. Динамічна форма може бути притаманна як нерухомим так і рухомим об'єктам. Динамічність робить форму активною, помітною, виділяючи її серед інших.

Статика - це стан спокою, рівноваги форми, стійкість у всьому її ряду, в самій геометричній основі. Статичність вимагає рівних спокійних ліній: мас, чітких членувань по горизонталі та вертикалі

Симетрія є одним з важливих засобів досягнення єдиності і художньої виразності форми. Симетрія - принцип організації, де елементи розташовані правильно відносно осі площини, або центру. Симетрія є дзеркальна і осьова.

Широко застосовується також асиметрія - розташування елементів, при якому вісь симетрії відсутня. Асиметрія - принцип організації площини, який базується на динамічній врівноваженості елементів, на враженні руху їх в межах цілого.

Симетрія і асиметрія допомагають досягти художньої виразності статичних і динамічних композицій.

Застосування принципів гармонії в художньому оформленні інтер'єру має велике значення. Гармонійна композиція полегшує сприйняття естетичної і змістовної інформації. На принципах гармонії ґрунтується композиційна побудова шрифтового, ілюстративних матеріалів.

Принципами, які визначають естетичну якість стендів, композиційну гармонійність, є повторення цілого в його частинах, відповідність розмірів, рівновага, ритм, пропорції. Принцип повторення цілого в його частинах полягає в наявності провідної ознаки в елементах композиції. Він забезпечує послідовність її сприймання й полегшує зміну зон уваги при переході від одних елементів до інших.

Принцип відповідності розмірів вимагає визначити спільну закономірність співвідношення частин і цілого в процесі сприймання. Цей принцип враховують при застосуванні планшетів прямокутної форми із співвідношенням 2 : 3, 3 : 4, 3 : 5 (близько до золотого перерізу), 9 : 10 (динамічний квадрат).

Принцип рівноваги забезпечує зрівноваження частин і цілого відносно просторової осі, головним чином по вертикалі, оскільки на сприймання впливає на?? земне тяжіння. Найпоширенішим способом забезпечення зрівноваження стендів є симетричне їх розташування відносно вертикальної або горизонтальної осі. Така композиція створює враження статичності. Центральний елемент композиції стає головним.

Також поширеною є асиметрична композиція. Вона дає можливість знаходити багатоваріантні рішення.

Важливе значення для будь-якої композиції мають такі художні засоби як пропорція - зв'язки між розмірами і ритм - повторення елементів, зв'язок відстаней.

Термін "архітектурний простір" використовується в професійній діяльності дизайнерів і архітекторів, наприклад, стосовно   відкритих міських просторів. Простір важливо й в інших областях архітектури й дизайну, особливо в дизайні інтер'єра. Проблема архітектурного простору є основною для дизайнера й архітектора. Сутність архітектури полягає в штучному відмежуванні природного простору.

Архітектура - це штучно створена людиною матеріально-просторове середовище, що володіє естетичними якостями. Архітектурне середовище складається з компонентів - маси, простору, стану середовища, освітленості, акустики, руху повітря. Поняття "архітектурний простір" складається із просторової форми, площин огородження й предметів устаткування. Архітектурний простір візуально обмежений у вигляді конкретної просторової форми.

Абсолютна величина простору в інтер'єрі подумки порівнюється з кількістю людей, які будуть перебувати в приміщенні. Для кожної людини виділяється "моторний простір", - це умовно обмежена частина загального простору для конкретної людини. Індивідуальне (моторне) простір вивчається ергономікою.

Як складова частина архітектурного простору, індивідуальний простір людини утворить групи й зони. Наприклад, у готелі виділяються зони адміністратора, зона очікування. Архітектурний простір завжди соціально виразно, у його основі лежить процес - торгівля, навчання, проживання, побут.

Поняття закритий або відкритий простір визначає взаємини архітектурних просторів і природних. "Закритий простір" означає фізичну ізольованість створеного простору від природного для забезпечення захисних функцій. "Відкритий простір" перебуває безпосередньо в природних умовах.

Поняття внутрішнього й зовнішнього простору визначає положення місця одного простору щодо іншого. Наприклад, вулиця - зовнішній простір стосовно   будинку. Існує термін "міський інтер'єр", або "інтер'єр відкритих просторів". Навіть внутрішній простір будинку може мати розподіл на внутрішні й зовнішні зони.

Архітектурний простір має важливу властивість орієнтації й спрямованості, динаміки свого розвитку. Орієнтація пов'язана з фізичними особливостями людини гравітацією, положенням у фізичному просторі, з поняттями низ, верх, спереду, позаду, збоку. Спрямованість простору виражається поняттями "низьке-високе", "вузьке-широке", " коротке-витягнуте. У кожну епоху прийоми художнього оформлення речей і критерії якості були різні, але загальним принципом завжди залишалася міра декоративного оформлення. Розуміння її криється в розходженні світогляду й світовідчування. Декоративна міра сучасного мистецтва - правдивість, стругаючи простота, уміння користуватися закономірностями застосування художніх засобів побудови предмета.

Відчуття спокою й стійкої рівноваги може дати симетрія, і навпаки, асиметрія викликає занепокоєння, неврівноваженість. Таке ж дія ритму: відчуття спокою викликає рівномірна повторюваність елементів, а порушення й нервовий стан - плутаний ритм.

 

 

 

 

2.3.  Симетрія і асиметрія в природі

Видатний математик Герман Вейль високо оцінив роль симетрії в сучасній науці:  “Симетрія, як би широко або вузько ми не розуміли це слово, є ідея, за допомогою якої людина намагалася пояснити і створити порядок, красу і досконалість”.

Що ж таке “симетрія”? Коли ми дивимося в дзеркало, ми спостерігаємо в ньому своє відображення - це приклад “дзеркальної” симетрії. Дзеркальне відображення -це приклад так званого “ортогонального” перетворення, що змінює орієнтацію(рис.20).

Рис.20

На явище симетрії в живій природі звернули увагу ще піфагорійці у зв’язку з розвитком ними вчення про гармонію.  Встановлено, що в природі найбільш поширені два види симетрії - “дзеркальна” і “променева” (або “радіальна”) симетрії. “Дзеркального” симетрією має метелик, листок або жук (Рис.2-а) і часто такий вид симетрії називається “симетрією листка” або “білатеральної симетрією”. До форм з променевою симетрією відносяться гриб, ромашка, соснове дерево (Рис.2-б) і часто такий вид симетрії називається “Ромашка-грибний” симетрією.

Рис. 21а                                              Рис.21б

Природні форми з “білатеральною” (рис.21а) і “радіальною” (рис.21b) симетрією.

Ще в 19-му столітті дослідження в цій галузі призвели до висновку, що симетрія природних форм значною мірою залежить від впливу сил земного тяжіння, яке в кожній точці має симетрію конуса. У результаті був знайдений наступний закон, якому підпорядковуються форми природних тіл:

“Все те, що зростає чи рухається по вертикалі, тобто вгору або вниз відносно земної поверхні, підпорядковується радіально-променевої (” Ромашка-грибний “) симетрії. Все те, що росте і рухається горизонтально або похило по відношенню до земної поверхні, підпорядковується білатеральної симетрії - “симетрії листка” (одна площина симетрії) “.

Симетрія в біології - це закономірне розташування подібних (однакових) частин тіла або форм живого організму, сукупності живих організмів щодо центру чи осі симетрії.

Асиметрія - відсутність симетрії. Іноді цей термін використовується для опису організмів, позбавлених симетрії первинно, на противагу дисиметрії - вторинної втрати симетрії або окремих її елементів.

Поняття симетрії і асиметрії альтернативні. Чим більше симетричний організм, тим менше він асиметричний і навпаки. Будова тіла багатьох багатоклітинних організмів відбиває певні форми симетрії, радіальну або білатеральну. Невелика кількість організмів повністю асиметричні. При цьому слід розрізняти мінливість форми (наприклад в амеби) від відсутності симетрії. У природі і, зокрема, в живій природі симетрія не абсолютна і завжди містить деяку ступінь асиметрії. Наприклад, симетричні листя рослин при додаванні навпіл в точності не збігаються.

Крім  геометричних елементів симетрії, розрізняють біологічні:

антімери - симетрично повторюються навколо головної осі монаксоно гетерополярность форм ділянки тіла;

радіус - площину симетрія антімера;

интеррадіус - площина, що проходить між сусідніми антімерамі;

метамери - повторювані ділянки, розташовані вздовж поздовжньої (зазвичай передньо-задньої) осі тіла організму.

Типи симетрій

Рис.22

Радиальна симетрія на прикладі медузи Chrysaora sp(рис.22).

У біологічних об'єктів зустрічаються такі типи симетрії:

Сферична симетрія - симетричність щодо обертань в тривимірному просторі на довільні кути.

Аксіальна симетрія (радіальна симетрія, симетрія обертання невизначеного порядку) - симетричність щодо поворотів на довільний кут навколо якої-небудь осі.

Симетрія обертання n-го порядку - симетричність щодо поворот ів на кут 360 ° / n навколо якої-небудь осі.

Двостороння (білатеральна) симетрія - симетричність відносно площини симетрії (симетрія дзеркального відображення).

Трансляційна симетрія - симетричність щодо зрушень простору в якомусь напрямі на деяку відстань (її окремий випадок у тварин - метамерія (біологія)).

Тріаксіальная асиметрія - відсутність симетрії по всіх трьох просторових осях.

 

Прояв симетрії в живій і неживій природі

Краса в природі не створюється, а лише фіксується, виражається. Розглянемо прояв симетрії з «глобального», а саме з нашої планети Земля.

Те, що Земля - куля, стало відомо освіченим людям ще в давнину. Земля в уявленні більшості начитаних людей до епохи Коперника була центром світобудови. Тому прямі, що проходять через центр Землі, вони вважали центром симетрії Всесвіту. Тому навіть макет Землі - глобус має вісь симетрії.

Далі  розглянемо прояв симетрії в живій природі. Майже всі живі істоти побудовані за законами симетрії, недарма в перекладі з грецького слово «симетрія» означає «відповідність».

Рис. 23 Поворотна симетрія на прикладі квітки

                                                                  "Ромашка"

Серед квітів, наприклад, спостерігається поворотна симетрія(рис.23). Багато квітів можна повернути так, що кожна пелюстка займе положення сусіднього, квітка сполучиться з самим собою. Мінімальний кут такого повороту для різних кольорів неоднаковий. Для ірису він дорівнює 120 °, для дзвоника - 72 °, для нарциса - 60 °. У розташуванні листя на стеблах рослин спостерігається гвинтова симетрія. Розташовуючись гвинтом по стебла, листя як би розкидаються в різні боки і не затуляють один одного від світла, хоча самі листя теж мають вісь симетрії. Розглядаючи загальний план будови якої-небудь тварини, ми помічаємо зазвичай відому правильність в розташуванні частин тіла або органів, які повторюються навколо деякої осі або займають одне і те ж положення по відношенню до деякої площини. Цю правильність називають симетрією тіла. Явища симетрії настільки широко поширені у тваринному світі, що дуже важко вказати групу, до якої ніякої симетрії тіла підмітити можна. Симетрією володіють і маленькі комахи, і великі тварини.

Серед нескінченного розмаїття форм неживої природи в достатку зустрічаються такі досконалі образи, чий вигляд  незмінно привертає нашу увагу. Спостерігаючи за красою природи, можна помітити, що при відображенні предметів в калюжах, озерах проявляється дзеркальна симетрія.

Бачите? Це ж гола дзеркальність!

 

Дурна, дурна природа, ні про що вона не дбає так завзято, як про рівновагу.

(Венедикт Єрофєєв)

 

 

 

 

 

 

 

РОЗДІЛ 3.

Симетрія в основі всього: в математиці, фізиці, хімії, біології, симетрія простору та часу

Провівши дослідження ми з'ясували, що симетрія і асиметрія нерозривні і доповнюють одна одну.

Симетрія широко зустрічається в об’єктах живої та неживої природи. Наприклад, симетрія в хімії відображається в геометричній конфігурації молекул. Так, наприклад, молекула метану СH4 володіє симетрією тетраедра. Поняття “симетрії” є центральним при дослідженні кристалів. При цьому симетрія зовнішніх форм кристалів визначається симетрією його атомної будови, яка обумовлює і симетрію фізичних властивостей кристала.

Особливо широко поняття “симетрії” стосовно фізичним законам використовується в сучасній фізиці. Якщо закони, що встановлюють співвідношення між величинами або визначають зміну цих величин з часом, не змінюються при певних операціях (перетвореннях), яким може бути піддана система, то говорять, що ці закони мають симетрією (або інваріантні) відносно даних перетворень. Наприклад, закон тяжіння діє в будь-якої точки простору, тобто він є інваріантним по відношенню перенесення системи як цілого в просторі.

На думку, вченого-енциклопедиста академіка В.І. Вернадського, “симетрія … охоплює властивості всіх полів, з якими має справу фізик і хімік”.

У світ неживої природи чарівність симетрії вносять кристали. Кожна сніжинка-це маленький кристал замерзлої води. Форма сніжинок може бути дуже різноманітною, але всі вони володіють поворотною симетрією і, крім того, дзеркальною симетрією.

 

  

Рис.24

  Симетрія в кристалах(рис.24)

А що таке кристал? Тверде тіло, що має природну форму багатогранника. Сіль, лід, пісок і т.д. складаються з кристалів. Перш за все Ромеєв-Деліль підкреслював правильну геометричну форму кристалів виходячи із закону сталості кутів між їх гранями. Він писав: «До розряду кристалів стали відносити всі тіла мінерального царства, для яких знаходили фігуру геометричного багатогранника ...» Правильна форма кристалів виникає з двох причин. По-перше, кристали складаються з елементарних частинок - молекул, які самі мають правильну форму. По-друге, «такі молекули мають чудове властивість з'єднуватися між собою в симетричному порядку».

Чому ж такі красиві і привабливі кристали? Їх фізичні і хімічні властивості визначаються їх геометричним будовою. У кристалографії (науці про кристалах) існує навіть розділ, який називається «Геометрична кристалографія». У 1867 році генерал від артилерії, професор Михайлівській академії в Петербурзі А.В. Гадолин строго математично вивів всі поєднання елементів симетрії, що характеризують кристалічні многогранники. (Форму куба мають, наприклад, кристали кухонної солі). Всього існує 32 види симетрій ідеальних форм кристала.

Легко уявити, яка б панувала на Землі плутанина, якби симетрія в природі була порушена

 

 

 

 

 

 

 

 

 

 

Висновок

У будь-якому виді мистецтва значне місце займає симетрія - засіб створення художнього образу, створення гармонії. Симетрія є одним з важливих засобів досягнення єдності і художньої виразності композиції в художньому проектуванні. З симетрією людина зустрічається повсякденно в природі і техніці, вона проходить через всю багатовікову історію людської творчості, її широко використовують архітектори, живописці, скульптори, художники-конструктори, інженери і навіть техніки, біологи, хіміки і т. д.

Симетрія, яку людина розкрила і осмислила у творіннях природи, ставала для неї поступово своєрідною нормою прекрасного. Вона починала свідомо використовувати її вже як засіб гармонійної організації форми. Саме як засіб композиції симетрія пройшла довгий шлях розвитку - від строгої канонізації (у багатьох східних культурах) до такої вільного трактування (наприклад, в епоху Відродження), коли слід говорити скоріше про складне композиційному рівновазі при збереженні за симетрією ролі організуючого фактору.

Людина вже на зорі цивілізації мала уявлення про симетрію, за її законами будувала свої споруди, виготовляла предмети побуту і все це визначалося не тільки практичними вимогами, але в якійсь мірі і естетичними. Потужні, урочисті єгипетські храми, світлі за образом стародавні грецькі будови, знамениті римські форуми і тріумфальні арки - всі ці споруди симетричні. У прикладному мистецтві це різні вази, чайні і кавові сервізи, багато прикраси. Численні приклади строгої симетрії можна знайти в розташуванні засобів та елементів художньо-політичного оформлення, Давні греки вважали, що Всесвіт симетричний просто тому, що симетрія прекрасна. Виходячи з міркувань симетрії, вони висловили ряд припущень. Так, Піфагор (V століття до н. Е..), вважаючи сферу найбільш симетричною і досконалою формою, робив висновок про сферичність Землі і про її рух по сфері. Ідея симетрії часто була відправним пунктом в гіпотезах і теоріях учених минулих століть, які вірили у математичну гармонію світобудови, та бачили в цій гармонії прояв божественного начала. Для давньоруської архітектури, наприклад, не характерна канонізація симетрії, і численні відступи наче покликані зв’язати форму храму з природою. Наштовхнувши людину на думку про використання симетрії для організації предметних форм, природа підказала їй і можливість відступу від суворого закону. Адже у формах самої природи постійно зустрічаються подібні відступи: одна клешня краба або раку помітно більша іншої, «малюнок» зебри не повторюється на двох половинах її тіла і т. д. Відомий математик Генріх Вейль глибоко досліджував симетрію як математичну закономірність. «Симетрія - в широкому або вузькому сенсі в залежності від того, як ви визначите значення цього поняття, - є тією ідеєю, за допомогою якої людина протягом століть намагався осягнути і створити порядок, красу і досконалість».

Поняття симетрія не обмежується симетрією об’єктів. Воно поширюється також на фізичні явища і керуючі ними фізичні закони. Саме симетрія дозволяє нам охопити найрізноманітніші тіла з єдиних позицій. Слово «симетрія» в перекладі з грецького означає «відповідність».

Симетрія - одне з найбільш яскравих і наочно проявляються властивостей композиції, засіб, за допомогою якого організується форма предмета (будівель, машин, верстатів, побутових приладів і т. п.) або композиції, де елементи розташовані правильно відносно площини, осі або центру. У симетрії дуже широкий діапазон можливостей і аспектів художньої виразності. Надаючи композиції урочистість, рівновагу і порядок, симетрія не заважає в той же час висловом експресії і динаміці форми.

Асиметрія і симетрія мають у формах природи різну силу звучання. Як говорить Г. Вейль, «… поняття дзеркальної симетрії починає розчинятися в неясному понятті врівноваженості (нім. Ausgewogenheit), понятті гармонійного творіння …». При конструюванні постійно доводиться стикатися з різними проявами симетрії, у тому числі і з такими, які Вейль як математик, який звик до точного мови математичного виразу, називає невиразним поняттям врівноваженості.

Симетрія і асиметрія допомагають досягати художньої виразності статичних і динамічних композицій. У художньому конструюванні постійно доводиться стикатися з різними проявами симетрії і асиметрії, бо за їх допомогою встановлюється певний порядок розміщення форм, пов’язаний із призначенням предмета, з тією роботою, яку він повинен виконувати і красою самого предмета. Практика пластичних мистецтв дає нам численні приклади найрізноманітнішого використання симетрії та асиметрії. В одних випадках композиція наближається до абсолютної симетрії. В інших, при наявності загальної симетричною основи, простежується явна асиметрія деталей. По-третє, навпаки, асиметрична в цілому композиція складається з симетричних частин. І нарешті, композиція може бути і в цілому, і в деталях повністю асиметрична.

У творчій практиці відхилення від симетрії зустрічаються значно частіше, ніж чиста симетрії. Причому відхилення ці є не стільки результатом функціональних вимог, скільки художнім прийомом посилення образної виразності композиції, її життєвої переконливості. Часто ці прийоми використовувалися в давньоруському мистецтві, а також майстрами народного декоративного мистецтва. Використовуються й тепер.

Симетрія і асиметрія при правильному їх використанні в композиції можуть стати найважливішим засобом вирішення об’ємно-просторових завдань і завдань гармонізації форм.

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Вейль Г. Симметрия./ Г. Вейль - М.: Наука, 1968. – 192 c., ил.

2. Подгорный А.Л. Симметрия как условие формообразования поверхностей оболочек./Республ.  межведомств.  научно-техн. Сборник «Прикл.  геом.  и инж.  графика».  Вып. 21./ А.Л. Подгорный - К.: «Будівельник», 1976. – с. 192.

3. Устин В.Б. Композиция в дизайне.  Методические основы композиционно-художественного формообразования в дизайнерском творчестве:  учебное пособие. – 2-е изд.,  уточ.  И доп./ В.Б. Устин – М.: АСТ: Астрель, 2007. – 239, [1] с.: ил.

4. Авторский дизайн интерьера.  Режим доступу: http://3dmax.1bs.ru/node/814.

5. Шафрановский И.И. Симметрия в природе. – 2-е изд.,  перераб./

И.И.Шафрановский – М.: Недра, 1985. – 168 с., ил.

6. Желудев І.С. Симетрія і її застосування. -М.: Энергоатомиздат, 1983р.

7. Компанеец А.С. Симетрія у мікро-і макросвіті. -М.: НАУКА, 1978р., 206с.

8. Підоу Ден. Геометрія і мистецтво М.: Мир, 1979р.

9. Сонин А.С. Осягнення досконалості: симетрія, асиметрія, діссімметрія,антісімметрія. -М.: ЗНАННЯ, 1987р., 208с.

10. Трофимов В. Введення в геометричному різноманітті з симетрії М.: МГУ 
1989р

11. Урманцев Ю.А. Симетрія природи і природа симетрії. -М.: ДУМКА, 1974р., 
232с.

12. Шубніков А.В. Вибрані праці з кристалографії. -М.: НАУКА, 1975р.