Матеріали до проведення вступного уроку з теми «Математика у розв'язуванні прикладних фізичних задач»

Матеріали до проведення ввідного уроку з теми «Математика у розв'язуванні  прикладних  фізичних задач»

Лекційний блок

Фізичне (механічне) явище і його модель, що ідеалізується; моделі, використовувані для опису руху транспортних засобів: рівномірний рух і рівноприскорений рух Математичні моделі для опису рівномірного і рівноприскореного руху. Лінійні і квадратичні залежності, їх графічне уявлення. Аналітичне і графічне вирішення лінійних і квадратних рівнянь. Лінійні і квадратичні залежності в кінематиці

Практичні заняття

Вирішення завдань по механіці (кінематиці), побудованих на матеріалі дорожньо-транспортних подій; завдання про ДТП за участю одного транспортного засобу, рухомого рівномірно і прямолінійно.

Завдання про ДТП за участю одного транспортного засобу, рухомого рівноприскорено.

Завдання про ДТП за участю двох транспортних засобів.

Ділова гра: участь експерта в судовому засіданні.

Самостійна робота: рішення або складання завдання, оцінка погрішностей результатів дослідження.

Матеріали практичних занять

Задача 2.22. Водій N, рухаючись по вулиці, зробив наїзд на пішохода. Згідно поясненням водія і свідченням свідків, пішохід (дитина семи років) вибіг із-за автофургона, що стоїть у узбіччя, у той момент, коли автомобіль, керований N, знаходився поряд із знаком, що обмежує швидкість руху 40 км/ч. Водій стверджує, що у момент наїзду він рухався з наказаною знайомий швидкістю.

Експертові поставлено питання: чи дійсно швидкість руху автомобіля була рівна  40 км/ч?

Проведіть дослідження і відповідайте на це питання.

До умови додається схема ДТП (рис. 2), спрощена в порівнянні з реальними схемами. Вона містить мінімум відомостей, необхідних для вирішення завдання. Приведені також відомості з довідкових таблиць про те, що швидкість руху семирічної дитини при бігу знаходиться в межах  9,3-15,6 км/ч.

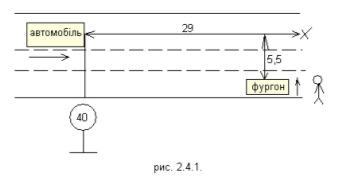
Розв’язання:

Відшукавши на схемі ДТП всі елементи дорожньої розмітки, згадані в умові об'єкти, відстані, слід сформулювати експертне питання завдання на мові фізики: «По відстанях, вказаних на схемі ДТП, і можливій швидкості руху дитини знайти швидкість руху автомобіля». Це завдання розпадається на дві: Знаючи відстань від автофургона до місця ДТП і можливу швидкість руху дитини, знайти час руху дитини від автофургона до місця ДТП; враховуючи знайдений час і відстань від дорожнього знаку до місця ДТП, знайти швидкість автомобіля.

Виберемо фізичну модель для опису руху дитини і автомобіля - рівномірний прямолінійний рух, при якому з швидкістю  за час  прямолінійного руху пройдений шлях, де .

З рівняння рівномірного прямолінійного руху виходить, що

Обчислимо можливий час руху дитини:

а) якщо  = 9,3 км/ч = 2,6 м/с. Тоді  = 5,5 м : 2,6 м/с = 2,1 з;

б) якщо =15,6 км/ч = 4,3 м/с, тоді = 5,5 м : 4,3 м/с = 1,3 с. Отже, можливий час руху дитини від автофургона до місця ДТП

знаходиться в інтервалі від 1,3 до 2,1 с.

Знайдемо можливу швидкість руху автомобіля, враховуючи, що відстань, яку він подолав, від знаку до місця ДТП складає 29 м:

а) якщо  =2,1с, то  = 13,8 м/с = 49,7 км/ч;

б) якщо = 1,3 з, то  = 22,3 м/с = 80,3 км/ч. Відповідь на питання завдання, з погляду фізики, звучить так: «Швидкість автомобіля (з урахуванням можливих значень швидкості дитини) лежить в інтервалі від 49,7 км/ч до 80,3 км/ч».

Відповідь з погляду експерта-криміналіста: «Швидкість автомобіля, керованого водієм N, перевищувала  40 км/ч».

Слід запропонувати учням пошукати інший варіант рішення задачі і підвести їх до графічного рішення. Це дає можливість показати використання графіків функцій, вивчених в курсі математики, в рішенні практичної задачі.

Побудуємо графік залежності відстані, пройденої дитиною, від часу (мал. 3, а). Графіком лінійної функції є пряма. Будуємо пряму по двох точках: початку координат  і крапці А, де 2,6 м - відстань, пройдена за 1 з і чисельно рівне швидкості руху дитини.

З побудованого графіка і відомої відстані від автофургона до місця ДТП (5,5 м) визначимо час руху дитини до моменту події, воно ж - час руху автомобіля від знаку, що обмежує швидкість, до місця ДТП. Не обчислюючи, позначимо відповідну крапку на осі  через .

Побудуємо графік залежності відстані, пройденої автомобілем, від часу. Графік - пряма, що проходить через дві точки: початок координат і точку з координатами, де 29 м –відстань від дорожнього знаку до місця ДТП. По графіку знаходимо значення відстані при . Це і є чисельне значення швидкості автомобіля у момент наїзду

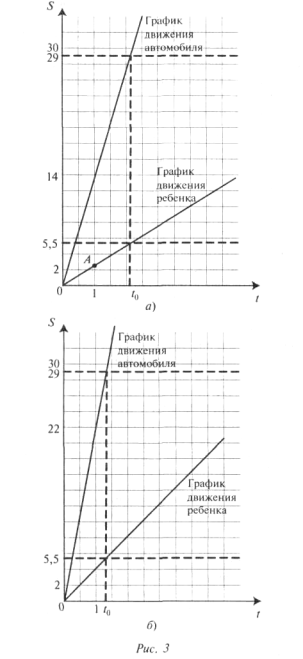
Аналогічно отримаємо швидкість автомобіля у випадку, якщо швидкість дитини складає 15,6 км/ч = 4,3 м/с (мал. 3, би). Швидкість автомобіля у момент ДТП рівна приблизно   22 м/с = 79,2 км/ч.

Таким чином, вирішуючи задачу графічним способом, ми отримуємо ту ж відповідь з погляду експерта-криміналіста: «Швидкість автомобіля, керованого водієм N, перевищувала 40 км/ч».

Відмінність в набутих значень швидкостей при рішенні аналітичним і графічним методами обумовлена погрішностями при побудові і читанні графіків, а також погрішностями, пов'язаними з наближеннями набутих значень.

Задача 2.23. Водій автомобіля «Ореl Vесtrа», що рухався вночі по крайній правій смузі заміського шосе, зробив наїзд на трактор, що стояв у узбіччя. Автомобіль рухався із швидкістю 90 м/ч з ближнім світлом фар. Водій стверджує, що застосував екстрене гальмування, але зупинитися не встиг. Експертові поставлено питання: «Чи мав водій автомобіля можливість уникнути зіткнення, застосувавши екстрене гальмування?»

У цьому завданні, на відміну від попередньої, розглядається ситуація, що часто зустрічається в експертній практиці, - учасник ДТП застосовує гальмування. Але встановити, чи проводилося гальмування, по наявності гальмівного сліду неможливо, оскільки автомобіль «Ореl Veсtга» оснащений антиблокувальною системою (пристроєм, що перешкоджає блокуванню коліс і входженню автомобіля в юз). Можливість уникнути зіткнення в даній ситуації визначається дальністю світла фар автомобіля «Оре1 Vесtга» і довжиною зупинного шляху.

Розв’язання:

Сформулюємо питання експертові на мові фізики: «На якій відстані автомобіль при екстреному гальмуванні, тобто при максимально можливому прискоренні, може понизити швидкість з 90 км/ч до 0? Більше або менше це відстань того, на якому водій мав можливість побачити перешкоду - трактор, що стоїть у узбіччя?»

Виберемо фізичну модель руху автомобіля під час гальмування - рівноприскорений рух. Звернемо увагу учнів на те, що водій не може почати гальмування в той же момент, коли він відмітив небезпеку. З моменту, коли небезпека виявлена, і до моменту, коли нога водія натиснула на педаль, проходить час, званий часом реакції . Час реакції залежить від багатьох причин: від того, наскільки несподіваною була для водія небезпека, від його психофізіологічних особливостей, рівня кваліфікації, часу доби, дорожньої ситуації. Зазвичай в розрахунках використовують середнє значення часу реакції, рівне 0,8 с. Для того, щоб повністю натиснути на педаль і щоб зусилля передалося з педалі на гальмівні колодки, також потрібний час, протягом якого гальмуюча сила і разом з нею прискорення (уповільнення) поступово наростають. Цей час називається часом наростання гальмівного зусилля  . Воно також залежить від багато чого: від конструкції гальмівної системи, якості і стану дорожнього покриття. У технічних розрахунках зазвичай вважають, що рух автомобіля починає сповільнюватися тільки після повного спрацьовування гальм. Для гальмівних систем з гідравлічним приводом час наростання гальмівного зусилля береться рівним   0,2 с.

Таким чином, виявляється, що вибрана модель руху потребує уточнення. У час, що складається з часу реакції і часу наростання гальмівного зусилля, рух автомобіля можна вважати рівномірним. При цьому він пройшов шлях s, за час   і мав швидкість . Після спрацьовування гальм, з моменту, коли гальмівне зусилля досягає максимуму, рух автомобіля був рівноприскореним з негативним прискоренням. А пройдений шлях дорівнював .

Записуємо рівняння рівномірного і рівноприскореного рухів (звертаємо увагу на фізичний сенс знаку «-» в другому рівнянні):

  і  .

Рівняння шляху, пройденого автомобілем з моменту виявлення водієм небезпеки до моменту зупинки:

(1)

Цей шлях носить назву зупиночного шляху, -час, який прийшов з моменту повного спрацювання гальм до моменту зупинки автомобіля.

Знайдемо, які данні необхідні для розрахунку зупиночного шляху. Прискорення знаходять в довіднику: а = 6,5 м/с², з умови задачі = 90 км/ч, = 0,8 с, = 0,2 с, а для визначення часу гальмування складемо ще одне рівняння — зміни  скорості в залежності від часу при рівноприскореному русі:

 (2)

Після запису рівнянь (1) и (2) необхідно ще раз впевнитися , що число невідомих в них дорівнює двом: та . Треба звернути увагу учнів на те, що на цьому етапі завершена фізична частина розв’язку задачі. Далі залишається виповнити лише математичні дії розв’язуючи систему рівнянь (1) и (2), знайти зупиночний шлях.

З рівняння (2) маємо . Для обчислень приведемо всі дані к одной системі вимірів

= 90 км/ч = 25 м/с, = 0 (в результаті гальмування автомобіль зупиняється ), тоді (с). З рівняння (1) маємо

(м).

Порівнявши довжину зупиночного шляху з відстанню, на якому водій  міг би побачити перешкоду, тобто з дальністю світла фар, яка складає  30 м при ближньому світлі, формулюємо висновок: «У даній ситуації водій не міг уникнути наїзду  за допомогою гальмування».

Розглянемо графічну ілюстрацію розв’язку  даної задачі. Вияснивши, що зупиночний шлях і час зупинки після спрацьовування гальм пов’язанні квадратичної залежності, скористаємося графіком квадратичної функції              у = Ах²+ Вх + С, вид якої аналогічній виду рівняння.

Незалежною зміною в цьому випадку є час,  який відлічується з моменту спрацювання гальмівної системи — моменту початку зниження скорості швидкості; коефіцієнт А дорівнює —, коефіцієнт В дорівнює  , роль параметра С грає доданок , постійне для кожного конкретного випадку (конкретної швидкості руху автомобіля, конкретного водія і конкретної гальмівної системи); функція у = — пройдений шлях з моменту початку відліку.

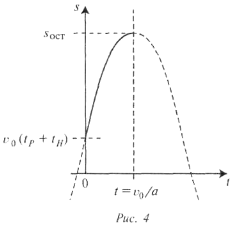Графік відобразимо схематично (рис. 4), визначаємо по значенням коефіцієнтів напрям гілок параболи, точки перетину кривої з координатними осями і абсцису вершини параболи.

Звернемо увагу, що математична модель в даному випадку відповідає фізичній реальності тільки на відрізку значень аргументу

 Тому що час не може бути від’ємним, не має фізичного сенсу частина кривої, яка лежить зліва від осі ординат. А шлях, пройдений тілом, не може з часом зменшуватись, тому не має фізичного сенсу й та частина кривої, котра відповідає значенням

Ці частини параболи на рисунку виділені пунктирною лінією. При досягненні часу (абсциса вершини параболи) швидкість автомобіля стає рівною 0, рух припиняється, і пройдена відстань у цей момент часу буде дорівнювати довжині зупиночного шляху.

Підставив данні задачі в побудовану модель, отримаємо рівняння Так як абсциса вершини параболи , знаходимо ординату вершини . Зупиночний шлях дорівнює 73 м.

Отриманий результат дозволяє зробити той же самий: «В ситуації, що склалася водій не міг уникнути наїзду за допомогою гальмування».