Збірка "Розв'язування олімпіадних завдань з математики за збірником О. Білянін "

ОЗ Великочернеччинська спеціалізована школа І-ІІІ ступенів Сумської районної ради Сумської області

 

 

 

 

 

 

 

 

Розв'язування  олімпіадних завдань

з математики за  збірником

О. Білянін 7 клас

 

 

 

 

 

 

 

 

 

 

 

 

Вчитель математики

 Саранчук О. В.

№1

Два прості числа називаються близнюками, якщо вони є сусідніми в ряду всіх простих чисел.   Довести, що будь-яке число, яке знаходиться  між близнюками і більше 4, ділиться на 6.

Розв’язання:

Наприклад близнюками є такі числа: 5 і 7; 11і 13; 17 і 19; 29 і 31 і т. д .    Нехай числа а і b-прості числа - близнюки і число р знаходиться між цими числами. Всі прості числа(крім 2)- непарні , тоді, якщо р стоїть між a і b,то р- парне,тобто ділиться на 2 і числа a,р,b – три послідовні числа. А із трьох послідовних чисел, одне якесь ділиться на 3. Так як а і b прості ,отже на 3 не діляться, тоді р- ділиться на 3 і ділиться на 2,отже р- ділиться на 6.                

№2

Яку найменшу   кількість будь-яких натуральних чисел потрібно взяти, щоб серед них  завжди знайшлася така пара чисел, різниця яких ділилася б на 5.

Розв’язання:

Потрібно взяти шість чисел. При діленні на 5 можливі такі остачі: 0;1;2;3;4  їх рівно 5. Отже , якщо взяти шість чисел, то обов’язково знайдуться  два  таких числа, які будуть мати  однакову остачу при діленні на 5, різниця цих чисел буде мати остачу рівну нулю,значить і буде ділитися на 5.

№4

На столі дві купки цукерок. У першій-12 цукерок,а в другій-13.Двоє грають у таку гру:за хід дозволяється або з’їсти 2 цукерки з однієї купки, або перекласти  одну цукерку з першої купки на другу. Програє той, хто не зробить хід. Довести,що при даних умовах починаючий завжди програє.                                         

Розв’язання:

Всіх цукерок  12+13=25 . Коли гравці будуть тільки  їсти цукерки ,то вони зроблять 25:2 =12 (ост  1),тобто 12 ходів – парну  кількість . Нехай відбулася  одна із ігор. Наприклад :

                                         12           13

1-й(з’їсть  2)                  12           11              2-й (перекладе) 3    8

2-й(перекладе)            11           12        1-й(перекладе)  2  9 

1-й(з’їсть)               9              12        2-й(з’їсть) 2 7

2-й (з’їсть)            7         12         1-й(перекладе) 1 8

1-й (з’їсть )           7          10        2-й(з’їсть) 1 6

2-й(з’їсть)           7            8        1-й(з’їсть) 1 4

1-й(з’їсть)           7            6       2-й(перекладе) 0 5

2-й(перекладе)           6            7        1-й(з’їсть) 0 3

1-й(перекладе)           5            8        2-й(з’їсть) 0 1

2-й(перекладе)           4                 9                             1-й- не може зробити хід

1-й(з’їсть)                     4                 7

Перший  програв  бо робив «непарні  ходи», другий  виграв бо робив «парні ходи».

Доведемо ,що  ходів  буде парна  кількість ,  тобто  останній  хід буде  парним. Кількість  ходів де гравці  з’їдають цукерки  парна,  бо їх 12.Тобто, при будь-якій грі, гравці  з’їдатимуть  цукерки  тільки за 12 ходів. Нехай    гравці  будуть  перекладати  цукерки ,  то  кількість цукерок  при цьому  не  змінюється , отже  з’їдати їх вони будуть за  12 ходів.  Скільки ж  можна  зробити  перекладань? Найбільше   12 . Нехай  гравці  зробили  12  перекладань,  знову парна  кількість, разом 12 «з’їданнями»  це 24 ходи, тобто парна кількість, отже  перший  програє . Нехай гравці зробили  11  перекладань. Але це неможливо, бо в першій  купці   залишиться  1 цукерка,яку  можна  тільки  перекласти  (перекладати  можна  тільки з першої купки ),  отже  всіх  перекладань  буде  12.Якщо перекладуть  10 цукерок, то    з’їдатимуть  тільки  за 12,разом за 22ходи, тобто знову за парну кількість ходів . Якщо перекладань буде 9,то з першої купки гравці 2 цукерки з’їли , отже знову залишиться  1  цукерка ,яку потрібно тільки перекласти , тобто всіх перекладань буде 10 . Якщо перекладали 8;6;4;2  цукерки,то це парна кількість, отже разом з 12, з’їданнями буде зроблена  парна  кількість  ходів і виграє другий . Якщо зроблено7;5;3;1 перекладань, то з першої купки  потрібно з’їсти  4;6;8;10- відповідно цукерок   і завжди буде залишатися  1 цукерка , яку потрібно  тільки перекласти . Отже всіх перекладань  завжди буде парна    кількість і всіх з’їдань  =12 - теж парна кількість . Значить і всіх ходів буде парна кількість . Тому  перший  завжди  програє .

№6

Для яких натуральних  х і у вираз  ху  приймає найбільше значення , якщо відомо що  х +у=11?    

Розв’язання:

Складемо таку таблицю,знаючи,що х +у=11 і х і у- натуральні числа. 

Х	1	2	3	4	5	6	7	8	9	10
у	10	9	8	7	6	5	4	3	2	1
ху	10	18	24	28	30	30	28	24	18	10

 Відповідь х₁=5;  х₂=6;
                    у₁=6;  у₂=5

 

 

 

№7

Катя  Софія,  Галя і Тамара  народилася  2 березня,17 травня,2 червня і 20 березня. Софія і Галя народилися в одному місяці, а  у Галі і Каті день народження  позначається  однаковими  числами. Хто якого  числа і в якому місяці народився?

Розв’язання:

Складемо  таблицю і позначимо  однаковий  місяць  народження (*), однаковий день  народження(v)

Ім’я
Катя	v		v
Софія	*			*
Галя	* v		v	*
Тамара

 

Ім’я
Катя	-
Софія	-
Галя	+	-	-	-
Тамара	-

 

Ім’я
Катя	-			-
Софія	-	-	-	+
Галя	+	-	-	-
Тамара	-			-

 

Ім’я
Катя	-	-	+	-
Софія	-	-	-	+
Галя	+	-	-	-
Тамара	-	+	-	-

 

№8

Довести нерівність:++++…+>

Розв’язання:

Якщо порахувати, то чисел від 1001 до 2000 включно рівно 1000 штук . Отже  ми маємо 1000 доданків . Порівняємо  кожен доданок з

> ;        >;    >; ….;=

Додамо  праві  і  ліві  частини  нерівностей :

++++…+   чи  ++++…+, отже  ++++…+ >++++…+, тоді :

++++…+

№9

Довести, що для будь-якого натурального n правильна рівність:

…+

Розв’язання:

Знаємо, що   ;   і т. д.

маємо

        ;      =. Отже рівність правильна при будь-якому n.

№10

За 500 гривень купили декілька пудів цукру. Якби на ті ж гроші було куплено п’ятьма пудами більше, то кожен пуд обійшовся б п’ятьма гривнями дешевше. Скільки куплено пудів цукру?

Розв’язання:

Нехай пудів куплено цукру.      (гривнів) – ціна одного пуда.

(гривнів) – ціна одного дешевшого пуда.  Тоді :

   = +5. Підбором знаходимо, що =20.

Відповідь: 20 пудів цукру.

№11

Чи існує трицифрове число ,що дорівнює добутку своїх цифр?

Розв`язання:

-трицифрове число . Тоді =100а+10в+с=abc . Значення 0 не можуть приймати ні a;ні b;ні c .         

1. Нехай a=1,тоді b може=1;2;3;4;5;6;7;8;9.Нехай b=1,маємо:                                                                            

100+10+c=11c ;   110+c=c, що не виконується . Нехай b=2, маємо: 100+20+с=2с,звідси                                

c=120-не є цифрою. Нехай b=3,тоді 130+с=3с, 2с=130, с=65-не цифра . Перевіркою

переконуємося ,що b  не може дорівнювати ні 4,ні 5,ні 6,ні 7,ні 8, і навіть не 9,бо при b=9, маємо:100+90+с+9с, 8с=190, с-не цифра .

2. Нехай а=2, b=1, маємо:200+10+с=2с, с=210-не є цифра,нехай b=2 , тоді : 200+20+2с=4с,  звідси с - теж не є цифрою . Переконуємося  ,що b не може дорівнювати ні 3,ні 4,ні 5,ні 6,ні 7,ні 8,ні 9.Бо при цих значеннях с не є цифрою . Аналогічно перевіряємо , що а не дорівнює  ні 3,ні 4,ні 5,ні 6,ні 7,ні 8,ні 9.При цих значеннях , якщо надати  b=1;2;3;4;5;6;7;8;9, то с не буде цифрою. Отже,не існує трицифрового числа,яке дорівнює добутку своїх цифр.

Або ІІ спосіб: =100а+10в+с=abc  Отже,    ,  але такого бути не може, бо в і с цифри.

№12

Якщо між цифрами двоцифрового числа вписати це саме число, то нове буде більше від даного в 77 разів. Знайти це число.

Розв`язання:

Нехай - дане число, тоді  - нове число. Маємо:                      а в

                                                                                                                 

                                                                                                            а а в в    

Підбором знаходимо, що в=5,  а=1

Відповідь: це число 15.

№13

Довести, що будь-яке трицифрове число, записане однаковими цифрами ділиться на 37.

Розв`язання:

Нехай - дане число записане одинаковими цифрами. Запишемо це число в вигляді суми розрядних доданків.   . Так як 111 ділиться націло на 37, то і будь-яке трицифрове число виду    теж ділиться на 37.

 №14

Знайти трицифрове число, яке у 12 разів більше від суми його цифр.

Розв`язання:

За умовою 

12а+12в+12с=     ;    88а-2в-11с=0.  Підбором знаходимо  а,в,с.

 1) а 0.   При а=1, маємо:  2в+11с=88,  при  в=0    ;  11с=88  ;  с=8.  Перебираємо далі всі в=1;2;3;4;5;6;7;8;9. Отримуємо, що  с-не цифра.

 2) При  а=2, маємо:  176=2в+11с,  якщо в=0, то с=176:11=16 – не є цифра, при всіх інших в маємо те саме, що і в попередньому пункті.    Наприклад  при найбільшому  в=9, маємо 11с=176-2158,   - не є цифра.

3) При а=3;4;5;6;7;8;9  і при будь-яких в від 0 до 9(в цифра), с10, не є цифра.  Відповідь: це число 108.                  

№15

Чи існує трицифрове число, квадрат якого дорівнює п’ятому степеню суми його цифр?

Розв`язання:

За умовою

1. Найменше трицифрове число 100 в квадраті =100000 (п’ять десяткових знаків), найбільше 999 в квадраті =998001(шість десяткових знаків)
2. Сума цифр  тризначного числа = від 1(це 100), до 27(це 999)
3. Знаходимо, що: 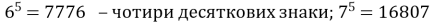;  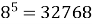   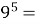 ;   59049  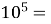 ; 100000 ;      ;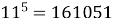  

   ;      ;  

      ;   - більше шести цифр.

4. З цих чисел жодне не є квадратом деякого тризначного числа.

Відповідь: не існує.

№16

Знайти натуральні значення n,при яких ділиться на n+3.  

Розв`язання:

Поділимо кутом    на  n+3.                                                  | 

                                                                                                    

                                                                                                    -

                                                                                                   - 

                                                                                                                9n+3

                                                                                                               

-24

                                                                             

Випишемо дільники числа 24:   1;2;3;4;6;8;12;24.  Тоді  n+3  може = 4;6; 8;12;24. Значить n=1;3;5;9;21.

Відповідь:  n=1;3;5;9;21.

№17

Розв’язати рівняння  ху+3х-5у=-3  в цілих числах.

Розв`язання:

у(х-5)+3х+3=0     ;   у(х-5)+ 3(х-5)+18=0    ;    (х-5)(у+3)=-18   Добуток двох цілих чисел =-18. Застосовуємо метод перебору.

   ;    ;     ;  ;

  ;   ;     ;    ;

  ;        ;  

Розв’язком цих систем є пари чисел: (6;-21),  (4 ;15),  (23;-4),  (-13;-2),  (7;-12),  (3;6),  (14;-5),  (-4;-1),  (8;-9),  (2;3),  (11;-6),  (-1;0).

№18

Довести, що рівняння  не має розв’язків в цілих числах.

Розв`язання:

         х(х-2у)=1978        Розпишемо 1978 на прості множники. 1978=2    

Застосуємо повний перебір

  ;    ;

     

Підставивши х в друге рівняння, отримаємо,що у не є цілим числом.

 

 

 

 

№40

Перша цифра чотиризначного числа 7. Якщо цю цифру переставити на останнє місце, то одержимо число, яке менше від початкового на 864. Знайти це число.

Розв`язання:

- початкове число. - одержане число. Тоді . запишемо цю різницю в стовпчик, маємо:       7авс               7681

                                                                               авс7               6817

                                                                                 864                864

Відповідь: шукане число 7681.

№ 41.

З вершини прямокутного кута проведемо 5 променів які проходять між його сторонами. Скільки гострих кутів утворилося?

Розв’язання: 90:6=15 – градусів містить найменший кут і їх всього 6. Беремо тепер кути утворені двічі по 150 градусів, тобто по 30 градусів; таких буде 5. Беремо кути утворені тричі по 150, тобто кути по 450, таких буде 4. Якщо взяти чотири рази по 150, то це 600.  Таких кутів 3. Якщо взяти п’ять раз по 150, це 750. Таких кутів 2. Отже всього кутів буде 6+5+4+3+2=20

 

№42

Знайдіть два натуральних числа, сума яких = 168, а їх найбільший спільний дільник = 24.

Розв’язання:

   Підбираємо два числа НСД яких =24

НСД (24;24)=24, але 24+24≠168 ;   НСД (48;24)=24, але 48+24≠168

НСД (72;24)=24, але 72+24≠168 ;  НСД (96;24)=24, але 96+24≠168

НСД (120;24)=24, але 120+24≠168 ;  НСД (144;24)=24, отже 144+24=168

НСД (48;72)=24, але 48+72≠168  ;   НСД (72;96)=24, отже 72+96=168

НСД (48;120)=24, отже 48+1201=168.

Всі інші числа НСД яких дорівнює 24 в сумі дають числа більше чим 168.

Отже це число (144;24); (72;96); (120;48).

№43

Побудуйте графік рівняння:

Розв'язання:

                                                                                          

Тоді х=0, або х+у=0, тобто х=-у

№44

 

Що більше:    чи    

Розв'язання:

Домножимо дроби так, щоб їх знаменники були однаковими, маємо:

  чи      Так як знаменники однакові порівнюємо чисельники, маємо:

(10¹⁰+1)(10¹²+1) чи (10¹¹+1)²

10²²+10¹⁰+10¹²+1 чи 10²²+2∙10¹¹+1

Однакові доданки зліва і справа можна знищити, тоді:

10¹⁰+10¹² чи 2∙10¹¹

10¹⁰(1+100) чи 2∙10∙10¹⁰

101∙10¹⁰  20∙10¹⁰.

Отже перший вираз більше другого.

№45

Розкладіть на множники многочлен:

А) х⁴+4

В) (a+b+c)³ – a³ – b³ – c³.

Розв'язання:

А)

x⁴ + 4=x⁴ + 4x² – 4x² + 4 = x⁴ + 4x² + 4 – 4x² = – 4x² = (x² + 2 – 2x)(x² + 2 + 2x)

 

B)

((a + b + c)³ – a³) – (b³ + c³) =(a + b + c – a)((a + b + c)² + a(a + b + c) + a²) – (b + c)         (b² – bc + c²) = (b + c)(a² + b² + c² + 2ab + 2ac + 2bc + a² + ab + ac + a² – b² + bc – =     =(b + c)(3a² + 3ab + 3ac + 3bc) = 3(b + c)(a² + ab + ac + bc) = 3(b + c)(a(a + b) + c(a + b)) = =3(b + c)(a + b)(a + c).

 

№46

Спростити вираз: (2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)(2³² +1).

Розв’язання:

Так як при множенні на 1 вираз не змінюється, то домножимо даний вираз на     (2-1)=1.

Тоді (2-1)(2+1)= - 1. Отже враховуючи це маємо:

 

№47

Не знаходячи x і y, обчисліть суму ; якщо x-y=4; xy=3.

 Розв’язання:

 

№48

Доведіть, що значення виразу ділиться на 10 при любому значенні n.

 Розв’язання:

  (*)

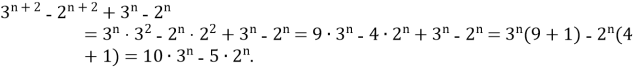Так як 10 - ділиться на 10, бо є множник 10 і 5 – теж ділиться на 10, бо – завжди парне число, а п’ять помножити на парне число буде число яке закінчуватиметься нулем.

Отже (*) буде ділитися на 10. Тоді і 10- 5 буде ділитися на 10.

№49

Якою цифрою закінчується сума +

Розв’язання:

Прослідкуємо якими цифрами закінчується  54¹³⁵ .  54¹=54;  54²=2916;   54³=…4

(закінчується на 4);  54⁴=…6 (закінчується на 6) і т. д. Тобто 54 в непарному степені

закінчується четвіркою, отже 54¹³⁵ закінчується 4.

Аналогічно:   28¹=28;          28²=…4;          28³=…2;          28⁴=…6;          28⁵=…8;

                         28⁶=…4; і т.д.

Тобто через чотири кроки іде повторення, отже якщо показник ділиться на 4, то число буде закінчуватися 6, якщо залишок одиниця, закінчуватиметься 8 і т. д.

 

21  4

20  5                   отже залишок одиниця, тоді 28²¹ закінчується цифрою 8.

1

Тоді 54¹³⁵+28²¹ буде закінчуватись 4+8=12 цифрою 2.

 

№50

Доведіть, що число ділиться на 10.

Розв’язання:

Знаходимо якою цифрою закінчується кожен із доданків.

  ;   ;     ; ;  і т. д. бачимо, що через 4 кроки цифра повторюється. Знаходимо остачу при діленні 99 на 4 , маємо число 3, тоді  закінчуватиметься числом 3. Аналогічно:

  ;   ;     ; ;    і т. д. бачимо, що через 4 кроки цифра повторюється. Знаходимо остачу при діленні 44 на 4 , маємо число 0 (тобто це числа кратні 4), тоді  закінчуватиметься числом 1. Аналогічно:

  ;   ;    і т. д. бачимо, що через 2 кроки цифра повторюється. Знаходимо остачу при діленні 88 на 2 , маємо число 0 (тобто це числа кратні 2), отже число буде закінчуватися числом 6. Тоді 3+1+6=10 число буде закінчуватися нулем, а отже буде ділитися на 10.

№51

При яких умовах графік функції  у= кх + в  має точки:

А)у трьох координатних четвертях;

Б)у двох четвертях;

В)в одні?

Розв’язання:

А)при к0 і в0, наприклад у=2х+1 і т.д.

Б)при в=0, наприклад у=2х, або при к=0,наприклад у=1,або коли у=0,а к0

і в0,тоді х=, це якесь число, наприклад, х=5 і т.д.

В) якщо0, у0, к 0(в також повинно приймати таке значення,щоб у

був більше 0),та їх комбінації. Наприклад , якщо у; або у=, якщо х і різні інші комбінації, або у=7, якщо х, і різні інші комбінації.

 

 

 

№52

Знайдіть всі значення параметра а , при яких система рівнянь      , не має розв’язків.

Розв’язання:

Система не матиме розв’язку коли перше рівняння  матиме вигляд  х + у = в, де в будь-яке число не рівне 1. Отже 2х+(9-2)у=6а -2

Запишемо як x+, тоді:

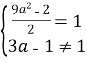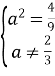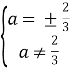     ;         ;        ;      ;  a=-

№ 53

Знайдіть двоцифрове число,квадрат якого дорівнює кубу суми його цифр.

Розв’язання:

Нехай це число =10а+в, тоді      (10а+в =(а + в  ;

100+20ав+=+3в+3а+;

1)Нехай а=1  маємо: 100+20в+=1+3в+3+

 +2-17в-99=0(*)

Серед дільників 99 (1;3;9;11;33;99) виділяємо цифри  це 1;3;9.Якщо

в=1,або в=3,або в=9 то рівність(*) не виконується.

2)Нехай а=2 маємо :400+40в+=8+12в+6+

 +5-28в-392=0(**)

Серед дільників 392(1;2;4;7;8;14;28…)виділяємо ті,які є цифри,це

1;2;4;7;8;. Перевіркою переконуємося, що в=7,тоді рівність(**) 

виконується. Отже це число 27

3) при всіх інших значеннях а і в умова не виконується.

Відповідь: 27

№54

Знайти всі двозначні числа, які зменшуються в 14 разів при

закресленні останньої цифри.

Розв’язання:

Нехай це число ,тоді  14а.      Підбором знаходимо а. Нехай 

а=1     маємо:      141=14=141=14     ;    а=2     маємо:    142=28=142=28

а=3      маємо:     143=42≠144≠42     ;    а=4     маємо:     144=56; 145≠56

а=5      маємо:    145=70; 147≠ 70     ;     а=6     маємо:      146=84; 148≠84

а=7      маємо:       147=98; 149≠98   ;     а=8     маємо:       148-не є

двозначним числом. Отже це число 14 і 28.

 

 

№55

Сума квадратів цифр двозначного числа дорівнює 10. Якщо від цього числа відняти 18, то отримаємо число, записане тими ж цифрами, але в зворотньому порядку. Знайти задане число.

Розв’язання:

Нехай - задане число. Тоді:

  ; ; ;

4+4в+2

в(в+3)-(в+3)=0

(в+3)(в-1)=0  , отже  не задовольняє умові задачі.  Тоді а=3

Відповідь: шукане число 31.

№56

Змішали 30%-ний розчин соляної кислоти з 10%- ним і дістали 300(г.) 15%- ного розчину. Скільки грамів 10%- ного розчину було взято?

 Розв’язання:

1. Знайдемо скільки кислоти міститься в 300(г.) розчину. 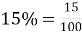, отже:   300:100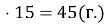
2. Нехай було х (г.) 30%-ного розчину кислоти, тоді (300-х) грам було 10 розчину кислоти.
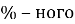
3. Знайдемо скільки кислоти в х (г.) 30%-ного розчину. Маємо:

             х(г.) кислоти  - 100

            А (г.) кислоти  -  30

Звідси  А

4. Знайдемо скільки кислоти в (300-х) грамах 10 розчину. Маємо:

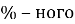
    (300- х)(г.) кислоти  - 100

            В (г.) кислоти          -  10

Звідси  В=

5. Отже всього кислоти буде: 0,3х+30-0,1х=45   ;     0,2х=15  ;   х=75(г.) – було 30%-ного розчину  ;  300-75=225 (г.) – було 10 розчину.

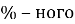
Відповідь: 225 (г.) – було 10 розчину.

№58

У вищій лізі чемпіонату країни з футболу бере участь 18 команд. Кожна команда зустрічається з іншою 2 рази за сезон. Скільки має відбутися усіх матчів ?

 

Розв’язання:

Всі команди (їх 18) в першому і другому колі зіграють 18=306 матчів, бо команда сама з собою грати не може. Відповідь: за сезон вони зіграють 306 раз.

 

 

№59

Ви розсипали в’язку  із 10 ключів від  10 дверей. Кожен ключ підходить тільки до одних дверей. Як за найменшу кількість спроб встановити відповідність між ключами і дверима?

Розв’язання:

Візьмемо перший будь-який ключ і будемо відмикати ним двері. В найгіршому випадку він підійде до останніх  дверей. Отже випробувань було 9. Другий до 9-х дверей, загальна кількість тут випробувань – 8 , третій – до восьмих дверей, випробувань – 7  і т.д. останній 10-й ключ підійде до останніх  дверей, випробувань – 0. Отже всіх спроб буде 9+8+7+6+5+4+3+2+1=45.

№60

У магазині є яблука в ящиках по 16, 17 і 21 кг. Як взяти 185 кг яблук, не відкриваючи ящики?

 Розв’язання:

1 спосіб    21кг5шт+16кг5шт=105кг+80кг=185кг.

2 спосіб    16 кг6+211+17кг4=96+21+68=185кг.

3 спосіб    16кг2+17кг9=32+153=185кг.

4 спосіб    16кг1+17кг5+21кг4=16+81+84=185 кг.

5 спосіб    21кг8шт+17кг1шт=168кг+17кг=185кг.

№61

Чи можна з усіх натуральних чисел від 1 до 100 вибрати 71 число, таким чином, щоб їх сума дорівнювала сумі решти чисел?

Розв’язання:

1. Знайдемо суму чисел від 1 до 100, таким чином:

(1+100)+(2+99)+(3+98)+…+(50+51)=101

2. Знайдемо суму чисел від 1 до71 так:

(1+71)+(2+70)+(3+69)+…+(35+37)+36=72.

Решта чисел від 72 до 100 в сумі буде мати 5050-2556=2494. Тому вибрати 71 число, щоб їх сума дорівнювала сумі решти чисел не можна, бо не можна зменшити першу суму 2556, бо ми взяли найменші доданки.

№62

Чи можна вивезти з каменоломні на семи тритонках 50 каменів, маси яких відповідно дорівнюють 370; 372; 374; …468 кг?

Розв’язання:

1. Всіх каменів 50 штук. Розіб’ємо їх по парах:

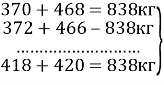215 штук.

Отже маса всіх каменів буде рівна:      838кг.

2. Сім тритонок візьмуть 7 кг. Але рівно по три тони розфасувати камені на машини не можно. Наприклад :

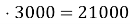
1)  3

2)  3

3)  3

4)  3

5)  3

6)  3

7)  1кг. Тому сьома машина не зможе взяти цей груз. І іншими способами не можна вивезти цей груз сімома тритонками.

№63

В одному з під’їздів  дев’ятиповерхового будинку на першому поверсі знаходяться квартири з номерами 65; 66;67 і 68. В якому під’їзді і на якому поверсі знаходиться квартира з номером 165?  

Розв’язання:

В умові мабуть помилка (восьмиповерхового), тоді в першому під’їзді буде 4квартири. В другому теж 32 квартири, всього 64 квартир. Тоді якраз в третьому під’їзді на першому поверсі і знаходяться квартири з номерами 65; 66; 67 і 68 і в цьому під’їзді теж 32, всього 96 квартир і 96 це номер останньої квартири. В 4 під’їзді теж 32 квартири, номер останньої квартири 96+32=128. В п’ятому під’їзді номер останньої квартири 128+32=160. Отже в 6 під’їзді на другому поверсі знаходиться 165 квартира.

 

№64

 

Доведіть, що з рівності a²+в² +c² = aв+вc+ca  випливає, що а=в=с.

Розв’язання:

a²+в² +c² = ав+вс+са /∙2 (ліву і праву частину множимо на два)

2 a²+2в² +2c² = 2ав+2вс+2са

a²-2ав+в² +a²  - 2ac+c²+в²-  2вc + c²  =0

(а-в) ²  + (а-с) ² + (в-с) ² =0

Так як усі доданки додатні(бо стоять в квадраті), то щоб сума дорівнювала 0  потрібно, щоб кожен доданок дорівнював 0. Значить (а-в)=0 і (а-с)=0 і (в-с)=0

        а=в          а=с в=с

Отже а=в=с.

№65

Скільки цифр містить число 2¹⁰⁰.

Розв'язання:

2¹⁰⁰ = (2¹⁰ )¹⁰= (1024²)⁵=(1048576)⁵. Так як перша цифра числа 1024 одиниця, а друга нуль, то це число в квадраті теж дає число перша цифра якого 1 друга 0 і із чотирьох цифр ми отримали сім. Отже 1048576⁵= 1048576∙1048576∙1048576∙1048576∙1048576. Тоді добуток першого і другого множника дають (сім цифр на сім цифр) 13 цифр. А 13 цифр на 13 цифр є 25 цифр і 25 цифр на 7 цифр = 31 цифра. Отже число 2¹⁰⁰  містить 31 цифру.

№67.

Доведіть, що всяке непарне число можна представити у вигляді різниці квадратів двох цілих чисел.

Розв’язання:

Непарне число це: 1;3;5;7;9;11;13…(2п-1)…, де п єZ, тобто пр.  п=1 ми отримуємо перше число 1, при п=2, отримуємо 3 і т.д. Нехай деяке непарне число (2п-1) можна представити як а²—в², де а і в деякі числа (цілі), отже а²—в² =2п-1, пєZ. Маємо:

(а+в)(а-в)=(2п-1)∙1. Тоді:          а-в=1      а=1+в        а=1+в     а=1+в

                                                    а+в=2п-1    1+2в=2п-1      2в=2п-2       в=п-1

а=1+п-1; а=п - ціле. Тоді а і в -  цілі числа. 

№ 68

Доведіть,що коли натуральне число має непарну кількість  додатних  дільників,то воно є точним квадратом.

Розв’язання:

Щоб записати дільники будь-якого натурального числа потрібно знайти перші ті дільники до тих пір поки деякі два в добутку дають саме це число,а потім шляхом ділення на записані дільники записуються інші. Наприклад :

48:  1; 2; 3; 4; 6;8;;;;                                 В даному випадку       маємо парну кількість дільників, і 6 і 8 є середина,яка складається з двох чисел. Якщо ж кількість дільників непарна,то серединою є одне число,в квадраті і дає це число . Наприклад   16: 1: 2: 4: 8: 16           і  16=                  

Отже будь-яке натуральне число яке має непарну кількість дільників є точним квадратом.

№70

Доведіть, що сума квадратів двох послідовних парних чисел при діленні на 16 дає в остачі 4.

Розв’язання:

Любе парне число позначається як 2n, nєN, тоді наступне парне число це (2n+2), за умовою (2n)² +(2n+2)²= 4n²+4n²+8n+4 = 8n²⁺8n+4 = 8n(n+1)+4, якщо n-непарне, то (n+1) – парне і навпаки, тому 8n(n+1) ділиться  на 16 і 8n(n+1)+4 при діленні на 16 дає остачу 4.

№72

Знайдіть усі прості числа p і q, для яких p²-2q²= 1

Розв’язання:

Із рівності p²-2q²= 1, маємо : p²-1=2q², або =q²:

Так як в правій частині рівності маємо добуток рівних простих чисел (q не має других дільників, крім q і 1), то і в лівій частині рівності маємо добуток рівних частин, тобто

 р-1=;     2р-2=р+1;    р=3.     Тоді     3²-2q²=1;     9-2q²=1:  2q²=8;    q²=4:  q=2  (q=-2 не задовольняє умові задачі).

Відповідь: р=3; q=2.

№75

Розв’яжіть в цілих числах рівняння: а) 8х-13у=15; б) х²  -  у ²=1990; в) х+у=ху

Розв’язання:

а) 8х=15+13у; х=Так, як (у+1) Є Z, то і - є ціле число. Позначимо  =а; аєZ, тоді 5у+7=8а; у==, позначимо =в, вєZ, тоді 3а-2=5в; 3а=5в+2  а=. Позначимо єZ, тоді 2в+2=3с і в=Позначимо Повертаємося на початок і знаходимо в, а, у і нарешті х. Маємо:

в=

 

y=Тоді х=

Відповідь:   х=    ;    у=, де n

б)   х²  -  у ²=1990  ;  (х-у)(х+у)=1990

Розписуємо 1990 на прості множники. 1990= 2. Застосовуємо метод перебору. Добуток  (х-у)(х+у)  може бути  1

і навпаки переставивши множники місцями. Тобто:

  ;  ; і т. д.

Розв’язуючи першу систему методом додавання маємо: 2х=1991;  х=995,5 – не є цілим числом, отже і у –  не  ціле число . Аналогічно  розв’язуючи кожну систему

переконуємося, що х і у дробові числа, значить рівняння  х²  -  у ²=1990  не має розв’язку в цілих числах.

в)  х+у=ху ;  х=ху-у  ; х= у(х-1)  ;  у(х-1)-х =0 ; у(х-1)-х+1 =0+1  ;

у(х-1)-(х-1) =1  ;  (х-1)(у-1)=1. Кожен із двох множників є ціле число і в добутку дає 1. Тоді:   ;  або  .  Маємо  ; або 

№76

Графічно та аналітично розв’яжіть систему рівнянь:

(1) ;      (2)  

Розв’язання (1):

1). Якщо і , то ;   

13 ; , тоді .   Отже система розв’язку не має.

2). Якщо , , то ; ; , тоді .      () – є розв’язок.

3). Якщо , то

  ;  - не є розв’язком

4). Якщо то 

  ; - не є розв’язком.

Розв’язання(2):

1).  Якщо , то   ; 

– не є розв’язком.

2). Якщо , то    ;  ,

тоді -не є розв’язком.

3). Якщо ; ; , тоді    Отже  (7;-3) – є розв’язком системи.

4).Якщо   то    ; 5y=-1+2(-2y+1) ; 

- не є розв’язком системи.

Відповідь:  (1) :   ,    (2) :  (7;-3).

Графічно:

 

 

 

 

 

 

№77

В ящику лежать червоні, зелені, сині та жовті кульки. Відомо, що червоних кульок в два рази більше, ніж синіх, синіх в два рази більше, ніж зелених, а число жовтих кульок більше 7 і менше 20. Скільки кульок кожного кольору знаходиться в ящику, якщо в ньому їх є 27.

Розв’язання:

=27 

Нехай зелених =х, тоді синіх буде =2х,а червоних =4х. Разом їх =7х.

Підбираємо х. Якщо  х=1,то разом червоних, зелених і синіх кульок буде 7, тоді жовтих буде 20, задовольняє умові задачі, значить червоних=4, зелених=1, синіх=2 і жовтих=20.

Якщо х=2, то разом червоних, зелених і синіх кульок буде  7, тоді жовтих= буде 27-14=13, задовольняє умові задачі, значить червоних=8, зелених=2, синіх=4 і жовтих=13.

 Якщо х=3, то разом червоних, зелених і синіх кульок буде  7, тоді жовтих= буде 27-21=6, не  задовольняє умові задачі.

№78

Доведіть, що добуток цифр багатоцифрового числа менший від самого числа.

Розв’язання:

Якщо число двоцифрове, то:   аb = 10а+b>a∙b, доведемо це.

1.  Якщо a=b, то  10a+a>a², 11a>a², 11>a, є правильна рівність, бо а – це цифра.
2. Даємо значення а і b від 1 до 9 переконуємося, що нерівність 10а+b>a∙b завжди виконується.
3. Якщо число багатоцифрове, то: 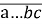= 10…0a+…+10b+c>a∙…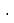b∙c (*). Перевіряючи пункти 1 і 2 з’ясовуємо, що нерівність (*) правильна. 

№80

Учень отримав завдання, що складається з 20 задач. За кожну правильно розв’язану задачу йому виставлять 8 балів. За кожну неправильно розв’язану – знімають 5 балів, а за задачу, яку він брався розв’язувати, –  0 балів. В сумі учень набрав 13 балів.  Скільки задач він брався розв’язувати.

Розв’язання:

Правильно розв’язані задачі

1 8бал. = 8 бал.    2 8бал  = 16бал.  3 8бал  = 24 бал.                              4 8бал  = 32 бал.            5 8бал  = 40 бал.             6 8бал = 48 бал.            Враховуємо те, що учень  отримав 13 балів. Отже  підбираємо скільки задач      він не розв’язав, при цьому  віднімаємо за кожну  неправильно розв’язану задачу 5 балів.  

16б – 51=11бал – не підходить

24б – 52=14 бал – не підходить

32б – 54=12 бал – не підходить,або 32б – 53=17б≠13

40б – 55= 156≠13

48б – 57=13балів

Отже учень правильно розв’язав 6 задач, неправильно розв’язав 7 задач і 7 задач він брався розв’язувати , бо 6+7+7=20.

 

№81

Групу школярів потрібно розмістити в їдальні. За столом має сидіти три чоловіки. Якщо садити за стіл по дві дівчинки , то виявиться три столи, за якими сидять лише хлопчики, а якщо садити за стіл по два хлопчики, то буде два столи, за якими сидять лише дівчатка. Скільки було дівчаток ?

Розв’язання:

Нехай х кількість дівчаток, тоді х/2 – це кількість столів за якими сидять по дві дівчинки, тоді (х/2 +3) – це  всі столи в їдальні.

В другому випадку маємо: два столи по три дівчинки це шість дівчаток, тоді їх (дівчаток) залишається (х – 6)  і кожна сяде за один стіл, тобто столів у їдальні буде 2+х-6, отже х/2 + 3 = 2 + х – 6  ;  х/2 +3 = х – 4 │ 2  ;  х + 6 = 2х – 8 ; х = 14—дівчаток.

 

№82

На лузі росте трава. На луг випустили 30 корів, які за 4 дні з’їли всю траву. Коли на лузі знову виросла трава, на нього випустили 25 корів, які з’їли всю траву за 6 днів. Яка найбільша кількість корів може пастися на лузі весь час (поки взагалі росте трава) ?

Розв’язання:

Нехай за один день наросте х кг. трави  і у кг. трави за один день з’їсть корова, тоді:           ,

 де а(кг) – кількість трави яка була на лузі  до того, як туди пустили корів. Від другого рівняння віднімаємо перше.

  а + 4х – 120у – (а + 6х – 150у)=0

  а + 4х –120у– а – 6х + 150у=0

30у = 2х           х =15у

Якщо шукане число корів n, то nу=х       n = х/у = 15у/у =15 корів.

Відповідь:  15 корів

 

№84

В мене в трьох коробка лежать цвяхи, гвинти і гайки. На кришці кожної коробки було написано, що в ній лежить. Одного разу мій молодший братик переставив кришки коробок так , що написи на них перестали відповідати вмістові коробок. Чи можна, відкривши одну з коробок, визначити , що лежить в кожній з коробок ?

Розв’язання:

Нехай маємо коробки з переставленими підписами.

Відкриємо коробку на якій написано цвяхи (там їх точно не має ), то там може бути:

а) гвинти, тоді там де написано гвинти цвяхів бути не може, бо вмістові третій коробці буде відповідати дійсність (гайки), отже в другій коробці гайки, в третій цвяхи.

б) гайки, тоді в третій коробці цвяхів бути не може, отже в третій коробці гвинти в другій цвяхи.

№85

Треба поділити 7 яблук на 12 чоловік порівну, розрізаючи кожне яблуко не більше, ніж на 5 частин. Як це зробити?

Розв’язання:

Треба розрізати 3 яблука на 4 рівні частини кожне, а 4 яблука – на 3 рівні частини кожне. Буде 12 четвертинок і 12 третинок. Отже кожен чоловік отримає по одній четвертій і по одній третій яблука.

№86

Чи можна розрізати квадрат на 6 менших квадратів? На 10 менших квадратів? На 13? (квадрати не обов’язково рівні між собою).

Розв’язання:

1	6
2
3	4	5

Можна.  Дивись малюнки.

1	2	6
3	4
5		7	8
		9	10

1		2		13
				12
3		4		11
				10
5	6	7	8	9

       

 

№87

Є 5 аркушів паперу. Деякі з них розірвали на 4 частини кожен, деякі з одержаних аркушів – знову на 4 частини і так декілька разів. Чи можна при цьому одержати 1984 аркуші ?

Розв’язання:

Очевидно після розривання одного аркуша паперу на 4 частини, загальна кількість аркушів збільшилася на 3. Отже, якщо таку операцію повторити n разів, то ми матимемо 5+3n аркушів. Якщо вважати, що 5+3n=1984 ; 3n=1979 але 1979 націло не ділиться на 3, так як n натуральне число. Отже підрахунок був неправильним.

№88

Остачу сірників знову подвоїли, а потім знову забрали 8 сірників. Коли ж таку операцію провели в третій раз, то в коробці не залишилось жодного сірника. Скільки сірників було спочатку В коробці лежали сірники,їх кількість подвоїли, а потім забрали 8 сірників.?

Розв’язання:

(2х – 8) – один раз

[2(2x – 8) – 8 ] – другий раз

[2(2(2x – 8) – 8 ) – 8] – третій раз = 0

2 (4х – 16 – 8) – 8 = 0

8х – 48 – 8 = 0

8х = 56   х = 7

№89

Сума 2000 цілих чисел непарна. Довести, що добуток цих чисел парне число.

Розв’язання:

Якби всі 2000 чисел були непарні, то їх сума була б парним числом (оскільки доданків парне число 2000), а за умовою їх сума непарна. Отже серед доданків є хоча б один парний. Тоді добуток цих чисел буде парне число.

 

№90

Для яких двоцифрових чисел сума куба цифри одиниць і квадрата цифри десятків дорівнюють самому числу ?

Розв’язання:

Нехай ab=10a+b дане двоцифрове число(a і b— це цифри). Тоді

b³+Нехай  а=1 :       b³+1=10+b ,тоді жодне з b=0,1,2,3,4,5,6,7,8,9. не задовольняють (рівність не виконується);

a=2 :       b³+4=20+b ,тоді жодне з b=0,1,2,3,4,5,6,7,8,9. не задовольняють

a=3 :       b³+9=30+b ,тоді жодне з b=0,1,2,3,4,5,6,7,8,9. не задовольняють

a=4 :       b³+16=40+b ; b³ – b =24   при b=3 маємо 27-3=24, 24=24.

Отже маємо число 43, дійсно 3³+4²=43.

a=5 :       b³+25=50+b   ,і b≠ 0;1;2;3;4;5;6;7;8;9

a=6 :       b³+36=60+b   , b³ – b =24   ,  b=3, тоді  це число  63.

a=7 , а=8 і а=9 — не підходять.

Відповідь : 43 і 63.

 

 

№91

Квадрат деякого натурального числа записується цифрами 0;2;3;5 (кожна цифра входить до запису числа тільки один раз). Знайти це число.

Розв’язання:

Нулем починатися воно не може, перебираємо всі числа. Знаємо, що квадрат будь-якого натурального числа не може закінчуватися 2;3 і одним нулем.

2035   3025   5023  Тільки одне число 3025=55²

2053   3052   5032

2305   3205   5203

2350   3250   5230

2503   3520   5320

2530   3502   5302

 

№ 92

У черзі в шкільному буфеті стоять Юра,Коля,Володя,Саша та Олег. Юра стоїть перед Колею, але після Олега . Володя і Олег не стоять поруч , а Саша не знаходиться поруч ні з Олегом, ні з Юрою,ні з Володею. В якому порядку стоять хлопчики?

Розв’язання:

1)Враховуючи , що Юра стоїть перед Колею після Олега маємо:  К;Ю;О     Буфет

2) Те ,що Олег і Володя не стоять поруч маємо два варіанти :   а)К;В;Ю;О    Буфет

                                                                                                            б)В;К;Ю;О    Буфет                

3)Сашко може стояти тільки перед Колею :                                  С;К;В;Ю;О   Буфет                                    

 

№93

Число 19 подати у вигляді  різниці кубів двох натуральних чисел. Довести що ця різниця єдина.

Розв’язання:

Нехай   а³ – b³= 19

(а – b)( а² + bа + b²)= 19∙1     ,  отже

   ;    ,   або    - розв’язку не має

Відповідь:  3³ – 2³= 19

№94

Прямокутник розрізається на два многокутники. Потім один з них знову розрізається на дві частини і т. д. Операція розрізання многокутників повторюється 661 раз. Після останнього розрізання підрахунок показав, що одержані многокутники містять всього 1983 вершини (вершина кожного многокутника рахується окремо). Чи правильно зроблено підрахунок?

Розв’язання:

Розпочнемо із випадку,коли всі одержані многокутники є трикутниками. Після першого розрізання число вершин дорівнюватиме 3+1, після другого - 3+29, після 662 – го – 3+662.

Якщо під час розрізання появиться хоч один многокутник відмінний від трикутника, то число вершин всіх одержаних многокутників буде більшим, ніж 1989. Отже підрахунок зроблено неправильно.

№95

На прямій взяли декілька точок. Потім між кожними двома сусідніми точками взяли ще по одній точці, і так декілька разів. Доведіть, що після кожної такої операції загальне число точок буде непарним.

Розв’язання:

Якщо на прямій взяти парне число точок, то відрізків, які ними визначаються, буде парне число. І якщо між кожними двома сусідніми точками взяти ще по одній точці, то цих точок буде непарне число. Тому сума числа тих і других точок буде непарним числом. Якщо ж точок на прямій – непарне число, то взятих між ними точок буде парне число. Кількість тих і других точок – непарне число і т. д.

№96

Знайти найменше натуральне число, сума цифр якого дорівнює 2000.

Розв’язання:

2000     9

18          222  

   20    

   18                             отже це число 2 99999...99

      20

      18                                                                         222 цифри

       ...  

№97

Нехай m i n – цілі числа. Довести, що коли ділиться на 1999, то це число ділиться також на

Розв’язання:

Число 1999 просте. Якщо  ділиться на 1999, то один із множників ділиться на 1999. Оскільки сума цих множників ділиться на 1999, то і другий множник ділиться на 1999.

№98

У записі натурального числа k використовуються тільки одиниці і двійки, причому одиниць в чотири рази більше, ніж двійок. Довести, що k +1983 складене.

Розв’язання:

Якщо число k закінчуватиметься 2, то число k +1983 закінчуватиметься п’ятіркою, отже буде ділитися на 5. якщо число k закінчуватиметься 1 то k +1983 буде парне, отже ділитиметься на 2. значить число k +1983 складене.

 

№ 99

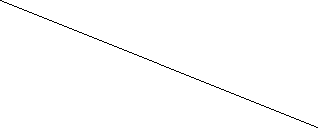
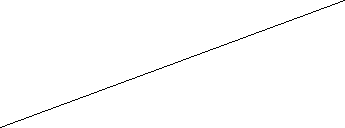
Розмістіть 6 точок на 4 прямих так , щоб на кожній з них було 3 точки.

  

 B K

 

Розв`язання:

Див. малюнок  шість точок : А;В;С;D;К;М.

на 1 прямій:А;М;D

на 2 прямій:А;В;С

на 3 прямій:С;К;М

на 4 прямій: D; К;В

№100

      а) Продавець одержав для продажу декілька пачок конвертів по 100 конвертів в кожній. 10 конвертів він відлічує за 5 секунд. За скільки секунд він відлічить 40 конвертів ? 50 ? 60 ? 90 конвертів ?            

Розв’язання:

40 конвертів за  4 ∙ 5 = 20 секунд

50 конвертів за  5 ∙ 5 = 25 секунд

60 конвертів  відраховуємо 40 і залишається 60, отже теж за 20 секунд.

90 конвертів відраховуємо 10 і залишається 90, отже за 5 секунд.

    б) встановити яке число треба поставити замість знака ? в послідовності 7;17; 37;77; ? ; 317;?;...

Розв’язання:

До 7 додали 10, потім додали 20, потім 40, потім 80, 160, 320… Маємо:

7⁺¹⁰ ;17⁺²⁰ ;37⁺⁴⁰ ;77⁺⁸⁰ ;  157⁺¹⁶⁰;317⁺³²⁰; 637⁺⁶⁴⁰

№101

Чи можна розмістити на чотирьох полицях 245 книжок так, щоб на першій полиці було на 12 книжок більше ніж на другій, на 17 книжок більше, ніж на третій, і на 15 книжок менше, ніж на четвертій?  

Розв’язання:

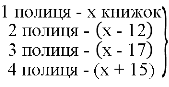=245. Складемо рівняння х+х-12+х-17+х+15=245

4х=259  ;   х= Отже так книги розставити не можна.

№102

До деякого двозначного числа зліва і справа приписали по одиниці. В результаті одержали число, в 23 рази більше від попереднього. Знайти дане число.

Розв’язання:

Нехай - задане число. Тоді . Запишемо цю рівність в стовпчик.

 

                   а   в                                                          7   7

                                

                .   .    .                                                    2    3   1

                                                           

            1  в   а   1                                              1   7   7    1

   Відповідь:   отже це число 77. 

№103

Побудувати графік функції .

Розв’язання:

                                                              

 

 

 

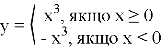
№104

Розмістити 10 точок на 5 прямих так, щоб на кожній було по 4 точки.

 4 

 3 A C

 

 E D

  Розв’язання:

Дивись малюнок. На першій прямій точки: E, K, L, В. На другій прямій точки:            Е, Р, N, C.  На третій – А, L, М, С.  На четвертій – В, М, N, D.

№105

Послідовність чисел будується за таким законом: на першому місці стоїть число 7, кожне наступне число – це сума цифр квадрата попереднього числа, збільшена на 1, тобто на другому місці стоїть число 14, оскільки , на третьому місці – число 17 і т.д. яке число стоїть на 2000 місці?

Розв’язання:

Третє число отримали так:   тоді 1+9+6+1=17. Маємо послідовність чисел: 7;14;17;25;8;11;5;… Бачимо, що починаючи з восьмого числа починається повторення через три кроки (без перших чотирьох цифр). Тоді 2000-4=1996. 1996:3=665(залишок 1). Так як залишок=1, то на 2000 місці стоїть число 5.

 

№106

Було 4 аркуші паперу. Деякі з них розрізали на 8 частин, потім деякі з цих частин знову розрізали на 8 частин і т. д. Коли підрахували загальну кількість аркушів, то виявилося, що їх всього 1986. Довести, що підрахунок був неправильним.

 Розв’язання:

Дивись розв’язання задачі №87.

При даному розрізанні матимемо 4+7п аркушів, тоді 4+7п=1986 і 7п=1982. А 1982 не ділиться націло на 7, отже п – не є натуральним. Значить підрахунок був неправильним.

 

№107

 

 

 

 

Сталеву плиту розміром 73обвели олівцем на папері. Знайти точку перетину діагоналей прямокутника, маючи лише цю плиту і олівець.

Розв’язання:

На обведеному прямокутнику, використовуючи сталеву плиту, відокремлюємо олівцем по краям два квадрати 19. Всередині отримали прямокутник 35. За допомогою плити проведемо діагоналі цього прямокутника їх точка перетину і є точкою перетину діагоналей обведеного прямокутника.

№108

Дано 125 натуральних чисел, попарно не рівних між собою і менших від 2000. Довести, що серед їх попарних різниць знайдеться хоча б 5 однакових.

Розв’язання:

Розмістимо ці числа в порядку зростання:   

Різниць виду  …; буде 124.

Різниць виду  …; буде 123.

Продовжимо цей процес. Нарешті різниця   одна і процес закінчується.

Всього цих попарних різниць  124+123+122+…+2+1=

Всі різниці менші від 2000. Отже, однакових різниць буде 7750-2000=5750 значно більше від 5.

№109

Обчисліть:

  Розв’язання:

=

№110

На дошці написана послідовність чисел: 3;8;15;24;35… За яким правилом утворені ці числа? Знайти наступні два числа.

Розв’язання:

8=3+5  ;  15=8+7   ;  24=15+9  ;  35=24+11  ;  35+13=48   ;  48+15=63…  Тобто до першого числа ми додали5, до другого 7, далі 9;  11; 13; 15; і т.д. 

№111

На лузі паслися 90 телят і гусей. Всього в них було 256 ніг. Скільки було телят і скільки було гусей?

Розв’язання:

Нехай телят було – х, тоді гусей було (90-х). Отже маємо:

4х – кількість ніг у телят,    2(90-х) – це ноги гусят. Тоді:

4х+ 2(90-х)=256     ;     4х+180-2х=256   ;    2х=76   ;   х=38 – ніг у телят,

(90-х) = 90-38=52 – ноги гусят.

 

№112

Чи можна розрізати квадрат розміром 6 на прямокутники розміром 1

Розв’язання:

Якщо квадрат розміром 6 можна розрізати на вказані прямокутники, то прямокутників повинно бути (6:4=9.

 Замалюємо квадрат так, як на малюнку, тоді кожен прямокутник 1 буде містити одну замальовану клітинку(між замальованими клітинками є три не замальовані як по горизонталі, так і по вертикалі). Але замальованих клітинок не 9, а 10. Отже неможливо розрізати квадрат розміром 6 на прямокутники розміром 1.

 

№113

На дошці було записано трицифрове число, яке починалося цифрою 9. Юрко поцікавився, як зміниться число від перестановки першої цифри на останнє місце. Виявилося, що одержане число на 216 менше відданого. Яке число було написане на дошці?

 

Розв’язання:

Записане число , нове число . За умовою                9 а в

                                                                                                    

                                                                                                    2 1 6

Тоді   в=5, а=7. Це було число 975.

Відповідь: 975   

 

№114

В деякій країні кожен член парламенту має в ньому не більше 3-х ворогів. Довести, що парламент можна поділити на 2 палати так, щоб кожен член парламенту мав в своїй палаті не більше одного ворога.

Розв’язання:

Розіб’ємо спочатку парламент на дві палати довільним способом. Нехай m i n – число пар ворогів в І-ій  і ІІ-ій палатах відповідно. Якщо в кожній із палат знайдеться член парламенту, який має в цій палаті не менше двох ворогів, то переведемо його в другу палату. При цьому одне з чисел n і  m зменшиться напевно на 2, а друге збільшиться не більше, ніж на 1. Отже, сума чисел   після такого переводу зменшиться. Оскільки ця сума не може зменшуватись нескінченно, то рано чи пізно одержимо розбиття, що задовольняє умові задачі.

№115

Знайти  двозначне  число, яке = подвоєному   добутку   його цифр.

Розв’язання:

Нехай   = 10а+в - дане  двозначне  число, тоді за умовою 10а+в =2ав.  Підбираємо  a так щоб і в теж було цифрою.

Нехай  а=1                  10+в=2в                  в=10- неможливо

              А=2                 20+в=4в                  в=   неможливо

              А=3                  30+в=6в                  в=6; це число 36

              А=4                  40+в=8в                 в=  неможливо

             і т. д   при всіх а=5… 9                  в – не цифра

    Відповідь: = 36.  

 

№116

Якщо між  числами  двозначного  числа вписати це ж саме число ,то одержане чотиризначне число буде більше  від даного в 77 разів. Знайти це число.

Розв’язання:

Нехай це число  , тоді за умовою                                                            а в

                                                                                                                       

                                                                                                                  а а в в

Так як двозначне число,помножити на двозначне = чотиризначне число, то  а=1, підбором знаходимо  в=5.  Тоді 1577=1155.

  Відповідь:15          

 

                                                                                    №117

Доведіть, що дріб   нескоротний при всіх натуральних n.

Розв‘язання:

  = = = .

Дріб   є нескоротнім , бо  це два послідовних натуральних числа . І дріб 1+= = є  нескоротнім, тоді і обернений дріб є нескоротнім.

Другий спосіб.  Розглянемо правильний вираз 2(n+1)=2n+2=(2n+1)+1. Якщо  дріб   скоротний, то n+1  i  2n+1 діляться на деяке число  m, а з правильної рівності слідує, що на m ділиться і 1, що неможливо.   

 

№ 118

Розмістити 9 точок на 10 прямих так, щоб на кожній прямій було по 3 точки.

Розв‘язання:

1. Будуємо довільний трикутник АВС;
2. Будуємо KL середню лінію трикутника АВС;
3. Паралельно сторонам через точки K і L проводимо прямі;
4. Через вершину В проводимо пряму паралельно АС;
5. Три прямі проводимо так, як на малюнку.

 

 

 

 

 

 

 

 

 

 

№ 119

Моторний човен пропливає відстань від А до В за 2 год., а відстань від В до А – за 2 год.  30хв . Визначити , за який час подолає цю відстань пліт , який рухає тільки  течія?

Розв‘язання:

 Нехай відстань від А до В =S км, x - швидкість течії річки ;

у - власна швидкість моторного човна. Тоді S=2 ( x+y )-плив човен від  А до В і

S= 2,5·(y-x) - плив човен від В до А , прирівняємо  величини:

                   2(x + y) = 2,5 (y-x) ; 2х+2y=  2,5y -2,5x ;

                   4,5x = 0,5 y ; 45x =5y ; y= 9x,тоді

S=2(x+ y)=2(x+9x)= 20х . Знайдемо за який час пліт подолає відстань А В. t =  = = 20 (годин)

Відповідь:  за 20 годин пліт  пропливе від А до В.

 

 

 

№120

В квадраті , що складається з 9 клітинок  , розмістити числа 1;2;3;4;5;6;7;8;9 так, щоб суми чисел, які стоять в кожному вертикальному, в кожному горизонтальному ряду, а також на будь-якій діагоналі, були рівні.

Розв'язання:

1. Знайдемо суму всіх чисел 1+2+3+4+5+6+7+8+9=45
2. Всіх 9 клітинок по три числа додаємо, маємо: 45:9∙3=15 – це сума по горизонталям, діагоналям і вертикалям.

 

8	1	6
3	5	7
4	9	2

 

№121

Пароплави першої лінії відправляються з порту через кожних 12 днів, пароплави другої лінії відправляються з порту через кожних 28 днів. 1               січня 2000 року два пароплави обох ліній вийшли з одного і того ж порту одночасно. Знайдіть найближчий день, коли обидва пароплави знову вийдуть одночасно з порту.

 Розв'язання:

Знайдемо НСК(12;28)=84 (найменше число, яке ділиться і на 12 і на 28). Отже пароплави вийдуть одночасно знову з порту через 84 дні. В січні 31 день. В лютому 29 (бо рік був цей високосним) і ще 24 днів березня. Отже пароплави знову зустрінуться 24 березня 2000 року.

№122

Задайте формулою лінійну функцію, графік якої паралельний осі абсцис і проходить через точку А(2.5;-6)

Розв'язання:

Графік функції паралельний осі ОХ(абсцис) має вигляд у=0х+в, тобто  у=в. Отже

у=-6.

Відповідь:  у=-6.

 

 

 

 

№123

Клоун сказав, що число кошенят, які живуть у нього, дорівнює  цього числа і ще   кошеняти. Слова про   кошеняти викликали сміх. Проте клоун сказав правильно. Скільки кошенят живе у нього?

Розв’язання:

Нехай було х кошенят. Тоді за умовою задачі маємо:

=х    ; множимо на 4  ;  3х+3=4х  ;  х=3.

Відповідь: 3

№124

Перша зліва цифра чотиризначного числа = 7. Якщо цю цифру переставити на останнє місце, то одержимо число, менше від даного на 864. Знайти це число.

Розв’язання:

Нехай це число , тоді нове число . Тоді                7 а в с

                                                                                                 

                                                                                           8 6 4

Знаходимо спочатку с=1, потім в=8 і а=6.

Відповідь: це число 7681.

 

 

№125

Чи можуть троє чоловіків, маючи двомісний мотоцикл, подолати відстань в 60 км за 3 години , якщо швидкість мотоцикла 50км/год., а пішохода 5 км/год.? Відповідь пояснити.                                            

Розв’язання:

Відповідь: можуть.

1) Мотоцикліст  бере пішохода і довозить за 1 годину в т. Д , далі пішохід  йде 2 години пішком рівно 10км і  приходить в т. В.

2) Мотоцикліст повертається за II пішоходом, який весь цей час іде. Мотоцикліст, який повертався із т. Д доїхав до С проїхав іще 40км тобто потратив на це менше чим 1 годину, отже пішохід тоді іще не дійшов до т. С. Якщо мотоцикліст його зачекає в т. С. ,то пройде рівно 2 години і вони за 1год. доберуться до т. В. Але мотоцикліст може рухатися за т. С. тобто назустріч пішоходу і тоді вони раніше доберуться до т. В.

№126

Знайти найбільше тризначне число,яке при діленні на 43 дає остачу,що дорівнює частці.

Розв’язання:

Розглянемо найбільше тризначне число 999.

999:43=23 (остача 10).

Візьмемо частку 22 меншу на 1 від 23,тоді і 946 +22=968

№127

В похід пішло 20 осіб: чоловіки,жінки і діти. Разом вони несли вантаж в 200 кг. Кожен чоловік ніс 20 кг вантажу,кожна жінка-5 кг,кожна дитина-3 кг. Скільки чоловіків,скільки жінок,скільки дітей пішло в похід?

Розв’язання:

Нехай х- чоловіки ,у-жінки,тоді -діти

0і .Знаючи хто скільки несе маємо:

20х+5у+3=200

20х+5у+60-3х-3у=200

17х+2у=140

За умовою х і у- натуральні числа. Отже шукаємо розв’язки рівняння в натуральних числах. Нехай  х=1;  2у=123; у-не натуральне число,отже-не може бути непарним числом.

х=2  ; 2у=106 у=53,але у-не більше 20.

При х=6  ; 2у=38 і у=19-тежнеможливо бо всіх 20

х=8  ;  2у=4 ; у=2-жінки, тоді дітей було 20 -=10

Відповідь:  чоловіків-8, жінок-2, дітей-10.

 

 

№ 128

На скільки частин можна розділити площину чотирма прямими?

Розв’язання:

На 5;  8;  9;  10;  11. Дивись малюнки.

 

 

 

 

 

 

 

№ 129

 

Побудувати графік функції  .

 y 4

 

 

 

 -2 2 x   

 

Розв’язання:

=.        Будуємо дві прямі на відповідних проміжках.

 

№ 130

        Квадрат із стороною 1 дм. відрізками розділено на 100 рівних квадратів. Якої довжини одержимо відрізок, якщо випрямити всю сітку, утворену сторонами квадратів?

 

 

 

 

Розв’язання:

Стовпці відділяються 11 відрізками і рядки відділяються 11 відрізками, отже всього відрізків (11дм=22дм. Або:

 

 

1. Розіб’ємо квадрат, як на малюнку, тоді сторона  

                                                                                  центрального квадрату  = дм., а його периметр

                                                                                  дм. Знайдемо периметри всіх виділених

                                                                                   квадратів.  дм., дм., дм.,

                                                                                  дм. (великий квадрат).

2.  В першому квадраті не враховані 4 сторони.

 Між першим і другим квадратами залишились не враховані сторони їх 12 шт., далі між другим і третім  20  шт., далі 28 шт., 36 шт. Всього їх довжина дм.  

 

Знайдемо довжину всіх відрізків дм.   

 

 

№ 131

Володя написав на дошці 1*2*3*… *9=21 ,поставивши замість кожної зірочки або «плюс» або «мінус». Сашко змінив деякі знаки на протилежні і в результаті  замість числа 21 написав число 20. Доведіть що один із хлопчиків помилився.

Розв’язання:

Якщо знаки поставити так:  1+2-3-4-5+6+7+8+9=21, то Володя може отримати 21. Так як 1+2+3+4+5+6+7+8+9=45, то щоб отримати 21 потрібно ,щоб 24 самознищувалося, бо 45-21=24, потрібно з даних цифр скласти 12 і -12. Наприклад ще один варіант              -    +  = 21

А Сашко не може  отримати 20, або 45-20=25 і щоб сума =20, потрібно, щоб 25 знищувалось, а це неможливо. З даних цифр неможна скласти 12,5 і -12,5. Отже, так як сума = 45 (число непарне) і якщо змінити знак в будь-якого доданка х, то сума зміниться на 2х і залишатиметься завжди числом непарним.

№132

Знайти трицифрове число , знаючи, що воно дорівнює ++.

Розв‘язання:

1)a, b, c – цифри не рівні нулю.

2)Сума трьох двоцифрових чисел = трицифровому числу, найбільше можливе

 99+99+99=297, отже a може бути або 1або2.Тоді

3)Якщо а=1, то щоб в першому стовпчику отримати с,в=9,тоді с=8

і =198=19+98+81.

 4)Якщо а=2,то знову в першому стовпчику,щоб отримати с в=8,тоді с- не цифра .     

Відповідь:=198

 

№133

Скількома нулями можуть закінчуватись числа вигляду +1, якщо n є N ?       

Розв’язання:

при п=1 маємо:+1=10 п=5 :           +1=59050

при п=2 :+1=82 п=6+1=531442

п= 3     :+1=730 п=7 :            +1=4782970

п=4 :+1=6562 п=8 :            +1=43046722

Отже при п - парному число+1 не буде закінчуватися нулем . При п –непарному закінчуватиметься одним нулем,бо число десятків даних чисел завжди є непарне це числа: 10; 730; 59050 …Тобто на місці десятків нуля не може бути.

№134

Довести, що будь-яке тризначне число, записати однаковими цифрами, ділиться на 37.

Розв’язання:

Нехай це число , запишемо в вигляді суми розрядних доданків. = 100а+10а+а=111а, так як 111 ділиться на 37, то і число ділиться на 37.

№135

Після того,як пішохід пройшов 1км і половину шляху, що залишився,йому

зосталося пройти третину всього шляху і один кілометр . Чому дорівнює весь

шлях?

Розв’язання:

Нехай весь шлях х(км), тоді він пройшов 1км,залишилося(х-1)км,а половина

цекм . Тоді зосталося пройти (+1)км і все це разом буде Х км( весь шлях)

1++ +1=х 5х+9=6х

6+3(х-1)+2х+6=6х х=9км

6+3х-3+2х+6=6х

Відповідь: 9 км.

№136

Розв’язати  рівняння:=+2

Розв’язання:

Розкриваємо знак модуля, знаємо що

 Тоді:

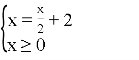або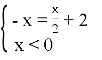 

                                     

                                               

 

  №137 

Маємо  прямокутну пластину масою в 10г.Яким чином можна розрізати її

на три частини з цілим числом грамів кожна так,щоб з їх допомогою можна

було,використавши терези без важків,визначити масу будь-якого предмета

в1,2,3…10 грамів?

Розв’язання:

Розділимо пластинку на 1гр+3гр+6гр=10 грамів.

Тоді предмет вага якого 1грам врівноважили пластиною в 1грам.

Предмет вага якого 2грами врівноважуватимемо пластинкою і першим

предметом вага яких по 1граму, тобто

2гр=1гр+1гр(це пластина і сам уже зважений 1гр предмет).

Аналогічно3гр=2гр+1гр( зважений предмет у 2грр і пластина1гр), або3гр=3гр(є пластина 3гр);4г=1гр+3гр; Щоб зважити предмет в 5г ми додамо до нього пластину в1г і врівноважимо пластиною в 6г, тобто 5гр+1гр=6гр;  7гр=6гр+1гр;   8гр+1гр=3гр+6гр ;  9гр=6гр+3гр  і 10гр=1гр+3гр+6гр.

Або пластинку можна розрізати на 1гр+2гр+7гр=10 грамів.

 

№138

Знайти двозначне число , яке в 4 рази більше від суми його цифр.

Розв’язання:

Нехай  – двозначне число . Тоді ; ba = 3b     2a = b при  a = 1

в = 2 ; при a = 2 ; b = 4  при  a = 3 ; b = 6 при  a = 4 ; b = 8. Але коли a = 5 ,то b – не цифра. Отже це числа  12 ; 24 , 36 і 48.

Відповідь: 12 ; 24 , 36 і 48.

№139

Чи можна розділити 13 аркушів паперу між шістьма учнями так, щоб при цьому кожний аркуш виявився розрізаний не більше , ніж на 3 частини ( або зовсім не розрізаний ) і кожний учень одержав однакову кількість шматочків паперу ?

Розв’язання:

Папір або не розрізається , або розрізається на 2 частини , або розрізається на 3 частини . В першому випадку 13 не ділиться на 6 , якщо розділити на 2 частини стане 26 шматочків , 26 теж не ділиться на 6 . Якщо розділити на 3 частини стане шматочків і 39 не ділиться на 6 .

Тобто якщо 13 ділити на 6 , то кожному дістається по 2 цілих аркуші паперу і ще  аркуша залишиться, тобто якщо брати половину і дві третини разом ми отримаємо цілу частину і шосту частину  + + = =

Значить нам треба ділити аркуші так  , щоб кожному дісталося по половинці , дві третини і цілий аркуш паперу . Тобто одному :

1 +   + + =    ;                6 = = 13 аркушів .

Відповідь: можливо.

 

№140

Відомо, що число  +173-1 ділити на 9.Чи можна скориставшись цим висновком, довести,що число+183-1 також ділиться на 9?

Розв’язання:

+183-1=+183-1=7(+173-1)-7173+7+183-1

При винесенні 7 за дужки в дужках ми написали той вираз, який за умовою

 ділиться на 9 . Доведемо,якщо  -7173+7+183-1 ділиться на 9,то і+183-1

також буде ділиться на 9.

-7173+7+183-1=-357+6+54=-357+60=-297  ділиться на 9. Отже +183-1 ділиться на 9.

Відповідь: можна

№141

Чи однаковий час потрібен для поїздки на катері (зі сталою швидкістю )на однакову відстань туди і назад по річці і по озеру?

Розв’язання:

Нехай швидкість катера =; швидкість течії річки =, відстань = S(туди за течією річки) і відстань = S(назад проти течії).     Швидкість за течією =.                                                                                                               Швидкість проти течії =              . Знаємо, що t=   , маємо:

 

	туди	назад
Час на озері
Час на річці

Запишемо загальний час по озеру: + =                                                               на річці: + = . Порівняємо величини  :

                                     і          

                                    

бо з двох дробів з однаковими чисельниками більший той, знаменник якого менший.

Відповідь: неоднаковий.

№142

Знайти найменше натуральне число,яке закінчується цифрою 6 і збільшується в чотири рази, якщо його останню цифру поставити на перше місце.

Розв’язання:

• Нехай це число двоцифрове: 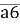,тоді нове 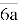,   маємо: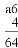- це виконується;
• Нехай це число трицифрове: 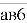,тоді нове 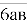,    маємо:              а в 6

                                                                                                                - не виконується.                                                                                        6 а 4

 

• Аналогічно це не чотирицифрове і не п’ятицифрове число.
• Нехай це число шестицифрове: 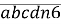, тоді нове 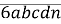. Маємо:   

      a b с d n 6                                       1 5 3 8 4 6

                                               

      6 a b с d n                                        6 1 5 3 8 4

Відповідь: 153846

№143

Скількома способами з відрізків довжиною  в 7см і 12см можна скласти відрізок довжиною 1 м?

Розв’язання:

Кратні 12:  12;24;36;48;60;72;84;96.Не вистачає до 100 :88;76;64;52;40;28;16;4; з цих

 чисел ділитися на 7 тільки 28. Отже можливо 100=126+728.  Або

Кратні 7: 7;14;21;28;35;42;49;56;63;70;77;84;91;98;

Не вистачає до 100 : 93;86;79;72;65;58;51;44;37;30;23;16;9;2

Ділиться на 12 тільки 72 тоді

100=126+74=72+28 це той самий спосіб.

Відповідь: одним способом.

 

№144

Знайти значення виразу:  + 0, 39-0,61+2x-0,22   при x=0,61

Розв'язання:

 -0,61+2x-0,22=+-0,61-0,61+2x+2-2,22=(x+1)-0,61(x+1)+2(x+1)-2,22=

=(х+1)(-0,61+2)-2,22=(0,61+1)()-2,22=1,61()-2,22=1,61

№145

Всередині плоского рівнобедреного трикутника АВС з основою ВС взято точку М, що МВС=, МСВ=. Знайдіть АМС, якщо ВАС=.

 

 

 

 

 

   

Розв'язання:

1. Приведемо бісектрису AD.
2. Продовжимо ВМ до перетину з AD, одержимо т. О.
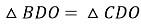
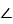
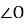
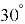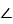
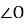
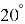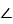
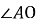
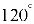3. (за першою ознакою), тоді ОВD=CD=. Тоді маємо, що ОCM=CA=.
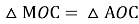
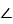
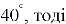
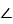
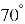4. MОC=C=. Тоді (за другою ознакою), значить АС=МС.
5. АСМ=  АМС=.

№146

Які цифри позначено буквами x, y, z, якщо добуток числа на число х  дорівнює

Розв'язання:

=100z+10 z+ z=111 z=3.  Звідси слідує, що .  Тоді , або. Перевіркою переконуємося, що х=3, у=7,  z=1.

№147

Дано смужку розміром 1, клітинки якої пронумеровані послідовними натуральними числами. Двоє учнів грають у гру, по черзі роблячи свої ходи. За один хід потрібно закреслити одну довільну клітинку в смужці або деякі дві послідовні клітинки, де перша з них має парний номер. Програє той, хто не може зробити хід. Хто може забезпечити собі виграш – починаючий чи його суперник? Вкажіть виграшну стратегію.

 Розв'язання:

Забезпечити собі виграш може починаючий. Розіб’ємо клітинки з номерами 2 – 17 на чотири набори по 4 клітинки. Перший гравець спочатку закреслює першу клітинку смужки, а потім діє аналогічно до другого: якщо другий закреслює клітинку з парним номером, то перший - іншу клітинку з парним номером з цього ж набору; якщо другий закреслює клітинку з непарним номером, то перший - іншу клітинку з непарним номером з цього ж набору; якщо другий закреслює дві  клітинки, то перший – інші дві клітинки з цього ж набору. Таким чином, перший гравець завжди буде мати можливість ходу.

№148

Довести, що вираз  є натуральним числом при будь-якому натуральному n.

Розв'язання:

Число ділиться на 9 тоді і тільки тоді, коли сума цифр даного числа ділиться на 9. Запишемо чисельник так: 1+8= 1. Сума цифр даного числа ділиться на 9. Отже число  при будь-якому натуральному n є натуральним.

№149

Розв’яжіть математичний ребус      

	Л	І	Т	О
+	Л	І	Т	О
П	О	Л	І	Т

 

 

Розв’язання:

1. Чотиризначне число + чотиризначне число = п’ятизначне, отже Л≠0; 1; 2; 3; 4.
2. Нехай Л=5, тоді П=1. Маємо

	5	.	.	.
+	5	.	.	.
1	.	.	.	.

Тоді 5+5 може закінчуватися або нулем,  або одиницею, якщо в попередніх розрядах сума була >10 і 1 пам’ятали але буква О не може бути 1, якщо О це нуль, то і Т теж нуль, що неможливо, отже Л≠5.

3. Міркуючи аналогічно Л≠6; 7; 9.

	8	.	.	.
+	8	.	.	.
1	.	.	.	.

4. Нехай Л=8   , тоді  П=1.  
5.  

 

	8	9	4	7
+	8	9	4	7
1	7	8	9	4

Тоді буква О або 6, або 7. Маємо

 

 

 

№150

АВС-  рівносторонній  трикутник. На продовженні  його  сторін  ВА,СВ,і АС  взято  відповідно  такі точки К; Е;Д, що АК=ВЕ=СД=.  Чи буде трикутник  ДЕК – рівностороннім ? 

 

 

 

 

 

 

 

Розв’язання:

 1)Так як ∆ABC-рівносторонній, то AB=BC=AC  і  A=B=C=60°

 2) За умовою AK=BE=CD ,  отже AD=CE=BK

 3) Кут КАD=180-60=120 і DCE =120 і  KBE=120

                                              4) трикутник KAD=∆DCE=∆KBE за двома сторонами  і кутом. Отже  KE =DE =KD,   тоді  трикутник KED -  рівносторонній.

№151

Чи можна розмістити в таблиці розміром 3числа (-1) та 1 так, щоб усі 7 сум чисел, що стоять в одному рядку або одному стовпчику були різними?

 

Розв’язання:

Можна наприклад:

1	1	1
-1	1	1
-1	-1	1
-1	-1	-1

 

 

№152

Дано чотири числа a, b, с, d, кожне з яких не дорівнює нулю. Кожне з перших трьох чисел множиться на наступне, а четверте множиться на перше. З новим набором проробляємо те ж саме. Довести, що завжди в кінці кінців отримаємо набір з додатних чисел

 Розв’язання:

Перша дія (другий набір) отримаємо: ab, bc, cd, da.

Друга дія: , , , .

Третя дія: , ,  ,  .

Четверта дія:  ,.

Всі множники в парних степенях, значить додатні, тоді додатні і їх добутки.

                                                                       №153

В  числі  12345123451234512345 закресліть 10 цифр  так, щоб залишилося найбільше   можливе число.

Розв’язання:

В даному числі залишиться  10цифр, отже закреслюємо цифри так , щоб на початку число мало найбільшу цифру, а це 5. Тому закреслюємо перші  1 2 3 4  і знову 1 2 3 4  матимемо 551234512345. Залишається закреслити дві цифри після п’ятірок 1 і 2 і матимемо число 5534512345.

№154

Квадрат розміром  77 заповнений числами так, що в кожному ряду добуток чисел є від’ємним. Довести, що хоча б в одному стовпці добуток чисел також є від’ємним.

 

Розв’язання:

1) Так як рядків сім і в кожному добуток чисел є від’ємним, то кількість чисел в кожному рядку є непарне, тоді загальна кількість всіх від’ємних чисел буде число теж непарне.

2) Допустимо, що в кожному стовпці добуток чисел додатній, тоді кількість від’ємних чисел в кожному стовпці парна. І загальна кількість всіх від’ємних чисел буде сім, раз додати парні числа буде число парне, що суперечить умові. Отже в одному із стовпців кількість від’ємних чисел непарна і добуток чисел буде від’ємним. Наприклад:

 

1	1	1	1	1	1	-1
1	1	1	1	1	1	-1
1	1	1	1	1	1	-1
1	1	1	1	1	1	-1
1	1	1	1	1	1	-1
1	1	1	1	1	1	-1
1	1	1	1	1	1	-1

 

№ 155

В мене є три відра, кожне з яких вміщує цілу кількість літрів. Якщо вилити повне перше відро води в друге, то вона займе його об’єму, а якщо вилити у третє, то вона займе його об’єму. Одного разу я наповнював бочку в 30 літрів, виливши туди послідовно перше, друге і третє відра води, але не наповнив бочки. Скільки літрів води ще треба долити?

Розв’язання:

Нехай в першому відрі х літрів. Тоді вода першого відра складає об’єму другого відра, отже в другому відрі   літрів,  аналогічно в третьому відрі   літрів. Якщо відра містять ціле число літрів, то х повинно ділитися і на 2 і на 3, отже на 6.

1. Нехай х=6л. – перше відро, тоді 9л. – друге відро і 8л. – третє відро. Разом 6+9+8=23, отже 30-23=7л. ще потрібно долити.
2. Нехай х=12л. -  перше відро, тоді 18л. – друге відро і 16л. – третє відро. Разом  12+18+16=4630 неможливо.

 

 № 156

Довести, що серед 101 цілого числа можна вибрати два таких числа, різниця яких ділиться на 100.

Розв’язання:

При діленні на 100 можливі такі остачі 0;1;2;3;4;…98;99 (всіх 100 штук). Тоді  серед 101 числа знайдуться два числа (принцип Діріхле), які при діленні на 100 дадуть однакову остачу. Різниця цих чисел і буде ділитися на 100.

 

№ 157

Якщо n натуральне число, більше за одиницю, то число не може бути квадратом натурального числа. Довести.

Розв’язання:

 

Допустимо, що є таке натуральне число а, що , так як непарне число, то і а теж непарне число. Позначимо . Тоді :

;

, ліву і праву частини поділимо на 2;

. За умовою n , тобто при найменшому n=2 число =2 кратне 2, а права частина не ділиться на 2. Отримане протиріччя доводить, що число не є квадратом натурального числа.

№ 158

Розв’язати рівняння: 

Розв’язання:

Розкиваємо знак модуля:

1);                     ;                 

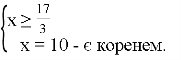
2);      ;

;      

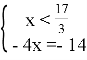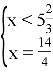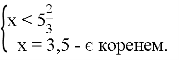
Відповідь:   ;  

№159

Знайти таке двозначне число, щоб куб суми його цифр = квадрату самого числа.

Розв’язання :

Нехай двозначне число. Тоді за умовою:

+3++=10+20ab+

1. Нехай  a=1 . Маємо: 1+3b+3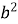+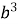=100+20b+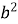

                                           +-17b-99=0

Серед  дільників вільного коефіцієнта :1;3;9;11;33;99; розв’язків не має, бо b є N.

2. Нехай  a=2. Маємо: 8+12b +6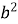+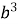=400+ 40b+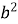

  дільники 392: 1; 2; 4; 7; 8; 14; 28; 49; 56; 98; 196; 392; b цифра, підходить b =7

перевіримо  число 27     ( 2+7 = ( 20+7 ;    = 2;   729 =729

3) Перебираючи  a=3… 9   цифри b не отримаємо.

Відповідь : a=2; b=7;   це число : 27  

№160

По колу, довжина якого 100 м, рухаються два тіла. Вони зустрічаються через кожні 20 секунд, рухаючись в одному і тому самому напрямі, і через кожні 4 секунди, рухаючись у протилежних напрямках. Знайти швидкості кожного із тіл.

Розв’язання:

Нехай х – швидкість першого тіла, у – швидкість другого тіла. Якщо вони рухаються по колу в одному і тому самому напрямку і зустрічаються, то це означає, що швидкість одного із них більша (нехай ) і тоді перший, коли наздожене другого, то він проїде на одно коло, тобто на 100 м. більше. Так як 20х – відстань, яку проїде перший за 20 секунд і 20у – відстань, яку проїде другий за цей же час, то різниця цих відстаней і буде повне коло тобто 100м. Отже  20х-20у=100.

Якщо вони рухаються в протилежних напрямках, то коли зустрічаються, разом проїдуть повне коло, отже 4х+4у=100. Маємо систему:

    ;      ;   2х=30   ;   х=15, тоді  15+у=25  і  у=10

Відповідь: швидкість першого 15, швидкість другого 10 метрів за секунду.

№161

Володя записав на дошці два числа. Трете число він написав рівним сумі перших двох, четверте – сумі третього і другого і т. д. Потім Володя повідомив Саші суму шести послідовних чисел, починаючи з деякого із записаних. Сашко, взнавши суму, зразу ж визначив одне з написаних чисел. Яке це число?

Розв’язання:

Перше число: a,   друге:  b, тоді:

Третє: ;

Четверте: ;

П’яте: ;

Шосте: .   

Їх сума = . В дужках п’ятий доданок.

Відповідь: Сашко визначив п’яте число.

 

№162

Один із суміжних кутів у три рази більший від їх різниці. Знайдіть градусні міри цих кутів.

Розв’язання:

Нехай х, у – суміжні кути (х менший), тоді сума суміжних дорівнює 180 градусів і за умовою більший кут у в три рази більший від різниці (у-х). Маємо систему рівнянь:

    ;      ;      ;      ; 

    ;      ;      ;      ;   .

Відповідь:  і .