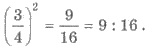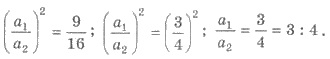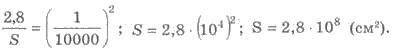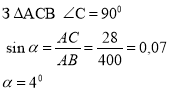Матеріали до уроків. ДобіМотивація на уроках геометрії у 8 класі . ІІ семестр.

Розділ ІІІ

Розв’язування прямокутних трикутників

Урок № 33

Тема уроку

Теорема Піфагора

Мета уроку

     Сформувати розуміння і знання теореми Піфагора, вміння записувати її  для знаходження однієї зі сторін прямокутного трикутника .

     Розвивати абстрактне та логічне мислення, математичну пам'ять .

     Виховувати уважність і спостережливість.

Прийом  І

Епіграф уроку

«Заняття геометрією непомітно приводить людський розум до винаходів. »

                                     Дені Дідро, французький філософ

Прийом  ІІ

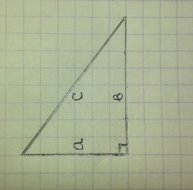
Геометричний експеримент.

       Учні першого варіанту накресліть в зошиті прямокутний трикутник, а другого - не прямокутний різносторонній трикутник. Виміряйте сторони даного трикутника, обчисліть квадрати сторін і порівняйте квадрат найдовшої сторони з сумою квадратів двох менших сторін. Учні роблять висновок, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів (в окремих випадках з деякою похибкою)

Прийом  ІІІ

Історична довідка (Цитата видатної людини)

         «Це він (Піфагор) довів до досконалості геометрію після того, як Мерид відкрив її начала(так пише Антиклід у ІІ книзі «Про Олександра ». Найбільшу увагу він приділяв числовому боку цієї науки. Він же відкрив і розмітку монохорда (музичний інструмент з однією струною); не зневажав він і науку зцілення. А коли він знайшов, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів , то приніс богам гекатомбу ( жертву 100 биків)» - Діоген Лаертський (Лаерцій) (ІІІ ст.) - давньогрецький  учений

         Учитель .  Пропоную учням на наступний урок зробити невеликі сповіщення у вигляді реферату, усного виступу, мульти – медійної презентації, відеоролика про Піфагора.

Прийом  ІУ

Прикладна задача

           Трансляційна вишка висотою 12 м закріплена за допомогою трьох розтяжок із дроту. Один кінець кожної з них закріплений на вершині вишки , а другий знаходиться на відстані 3 м від її основи. Скільки метрів дроту знадобилось для виготовлення розтяжок?

Урок № 34

Тема уроку

Теорема Піфагора

Мета уроку

         Домогтися засвоєння учнями правил знаходження невідомих сторін прямокутного трикутника застосовуючи теорему Піфагора. Повторити властивість катета прямокутного трикутника, що лежить проти кута 30⁰. Прищеплювати інтерес до історії математики. Виховувати наполегливість у здобутті знань .

Прийом  І

Історична довідка (Мульти – медійна презентація)

Прийом  ІІ

Міні – лекція

         1974 року до сузір'я Геркулес із Землі було відправлено потужний радіосигнал, який містив у собі 1679 найважливіших повідомлень і відкриттів. Серед них було зашифровано і теорему Піфагора.

Але дізнатись про те, чи змогли інші істоти зрозуміти цю теорему, зможуть тільки через 5 тисяч років. Саме через ней час сигнал повернеться на Землю.

А як зрозуміли ви теорему Піфагора, з'ясуємо на уроці .

Урок № 35

Тема уроку

Теорема Піфагора

Мета уроку

Домагатись міцного знання  теореми Піфагора .

Розвивати вміння доводити та застосовувати теорему Піфагора. Виховувати культуру математичних записів і мовлення.

Прийом  І

Ігровий момент

Учні виконують  на папері в клітинку запропоновані рисунки , обговорюють  фігури та їх площі, попередньо пригадавши про площу квадрата.

Прийом  ІІ

Практична вправа.

  Мотузку довжиною 6 м розділити за допомогою вузлів чи маркуванням на 12 рівних частин. З допомогою двох учнів утворити трикутник зі сторонами 3, 4, 5 частин. Переконуємось, що трикутник – прямокутний.

Учитель :  Прямокутний трикутник зі сторонами 3,4,5 був відомий стародавнім єгиптянам. Вони ним користувались під час земле вимірювальних робіт. Поділивши вірьовку на 12 рівних частин , закріплювали її кілками в поділках, які від одного кінця відділяли 3 частини, а від другого – 5. Натягуючи вільні кінці вірьовки та суміщаючи їх, діставали прямокутний трикутник з прямим кутом між відрізками 3 і 4 одиниці. Людей , які займались цією справою , називали гарпедонаптами (Натягувачі вірьовок), а прямокутний трикутник зі сторонами 3,4,5 дістав назву – єгипетський.

  Подумайте, де ви можете використати ці знання.

Прийом  ІІІ

Прикладна задача

Фронтон має форму рівнобедреного прямокутного трикутника з основою 12 м. Чи вистачить 3 кг фарби , Щоб пофарбувати цей фронтон, якщо витрати фарби становлять 95 г/см².

Урок № 36

Тема уроку

Перпендикуляр і похила, їх властивості

Мета уроку

        Сформувати в учнів свідоме розуміння змісту понять похилої до прямої, проекції похилої на пряму, а також властивостей перпендикуляра, похилих та їх проекцій.

        Сформувати вміння:  відтворювати зміст вивчених понять;  знаходити названі геометричні об'єкти на рисунку;  виконувати рисунок із зображенням названих об'єктів за даним описом;застосовувати   формулювання   властивостей   перпендикулярів, похилих та проекцій для розв'язування задач.

     Розвивати уяву.

      Виховувати культуру виконання геометричних рисунків.

Прийом  І

Геометричний експеримент.

       Накресліть в зошиті пряму, точку що не лежить на даній прямій, опустіть перпендикуляр з даної точки до даної прямої. По обидва боки від цього перпендикуляра проведіть дві рівних похилих. Ще одну похилу проведіть не рівну даним.

        Зробіть вимірювання довжин перпендикуляра, похилих, їх проекцій і сформулюйте висновок: які співвідношення існують між довжинами перпендикуляра, похилих, їх проекцій.   Учні формулюють твердження.

Урок № 37

Тема уроку

Перпендикуляр і похила, їх властивості

Мета уроку

 Формувати вміння учнів застосовувати теорему Піфагора, властивості перпендикуляра та похилої під час розв'язування задач; вдосконалювати навички шукати шляхи розв'язування задач; розвивати пізнавальні здібності учнів, логічне мислення, показати зв'язок геометрії з життям; уміння і навички аналізувати, робити висновки; виховувати активність, самостійність, спостережливість, увагу, інтерес до математики, вміння спілкуватися, почуття відповідальності.

Прийом  І

Учитель. За легендою, Піфагор був непоганим спортсменом і навіть чемпіоном олімпійських ігор з кулачного бою. Тому розв'яжемо задачу про спорт.

Задача. На протилежних берегах річки стоять двоє стрільців. Зріст одного становить 180 см, другого — 120 см. Ширина річки — 500 см. Обидва стрільці одночасно випускають стрілу з лука, влучаючи в один момент у мішень на поверхні води, що лежить на прямій, яка сполучає ступні стрільців. Знайдіть довжини шляхів стріл та місце знаходження мішені.

Урок № 38

Тема уроку

Розв’язування задач. Самостійна робота .

Мета уроку

           Домогтися засвоєння учнями поняття похилої та її проекції.

           Довести властивості похилих, проведених з однієї точки до прямої, і їх проекцій.

           Формувати вміння і навички застосовувати набуті знання до розв'язування задач.

           Розвивати творчу ініціативу та розумові здібності учнів, самостійність, культуру спілкування, математичне мовлення, вміння міркувати, порівнювати, робити висновки, узагальнювати.

           Виховувати почуття колективізму, відповідальності, наполегливість у досягненні мети, віру у свої сили, інтерес до математики через ознайомлення з відомостями з історії геометрії.

Прийом  І

Слово учителя

        Щодня у своєму житті кожна людина має справу з багатьма завданнями, які неможливо виконати без знання математики, тобто без розв'язування різноманітних задач. Проте для цього треба знати теоретичний матеріал. Сьогодні на уроці ми дізнаємось, наскільки добре ви його вивчили і хто з вас зможе подолати « віслючий міст».

        Що таке «віслючий міст»?

        У давнину теорему Піфагора називали « віслючим мостом», оскільки учнів, які завчили теорему напам'ять, але не вміли її застосувати, називали віслюками. Для них теорема Піфагора була ніби непрохідним мостом. Бажаю вам усім перейти цей міст.

Урок № 39

Тема уроку

Співвідношення між сторонами і кутами в прямокутному трикутнику

Мета уроку

Домогтися розуміння і засвоєння учнями змісту означень синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей , що випливають з теореми Піфагора, подібності прямокутних трикутників та властивостей прямокутного трикутника( проти більшої сторони лежить більший кут і навпаки).

     Сформувати вміння відтворювати зміст означень та їх властивостей, а також знаходити значення тригонометричних функцій гострого кута за допомогою прямокутного трикутника.

     Розвивати абстрактне логічне мислення.

     Виховувати цікавість до вивчення математики.

Прийом  І

Міні – лекція

       У цьому розділі ви дізнаєтесь, як розв’язувати прямокутні трикутники, тобто знаходити їх сторони й кути за відомими. Необхідні для цього теоретичні знання можна почерпнути з розділу математики , спорідненого як з геометрією, так і з алгеброю, - тригонометрією. Власне , саме слово «тригонометрія» в перекладі з грецької означає «вимірювання трикутників». Тому відношення сторін прямокутного трикутника, з якими ви познайомитесь далі, отримали назву тригонометричних функцій.

        Співвідношення , які будуть застосовувати в цьому розділі,  повною мірою можна вважати проявом подібності трикутників. Узагалі, подібність трикутників, теорема Піфагора і площа – це ті три кити, на яких тримається геометрія многокутника. Саме встановлення взаємозв’язків між цими теоретичними фактами і становить основний зміст курсу геометрії у восьмому класі

Урок № 40

Тема уроку

Співвідношення між сторонами і кутами в прямокутному трикутнику

Мета уроку

Домогтися засвоєння учнями означень синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей; розглянути тригонометричну тотожність та наслідки з неї; формувати вміння перетворювати тригонометричні вирази за допомогою тригонометричних тотожностей.

     Розвивати абстрактне мислення.

     Виховувати спостережливість та уважність.

Прийом  І

Проблемно-практичне завдання.

Виконайте зображення прямокутного трикутника з ка­тетами а, b і гіпотенузою с. Кути, протилежні катетам а і b, позначте відповідно α, β. Запишіть відношення, яким дорівнюють tgα та ctgα. Порівняйте записані відношення. Що ви помітили? Чи зміниться результат, якщо взяти інший прямокутний трикутник? Сформулюйте здобутий результат у вигляді твердження.

Мета запропонованого завдання — наочно продемонструвати учням існування певних залежностей між тригонометричними функціями деякого гострого кута. Далі вчитель наголошує на тому, що для інших тригонометричних функцій (крім тангенса і котангенса) одного й того самого кута також існують певні залежності; їх вивчення і становить основну мету уроку.

Прийом  ІІ

Прийом  ІІІ

Проблемна задача

       Доведіть теорему Піфагора за допомогою тригонометричних функцій гострого кута прямокутного трикутника і основної тригонометричної тотожності

Урок № 41

Тема уроку

Співвідношення між сторонами і кутами в прямокутному трикутнику

Мета уроку

      Закріпити знання учнями формул доповнення та числових значень тригонометричних функцій кутів 30⁰, 45⁰, 60⁰. 

    Сформувати та розвинути  вміння застосовувати формули до розв’язування задач.

     Виховувати уважність та спостережливість

Прийом  І

Мозковий штурм

    1 )Накресліть рівнобедрений прямокутний трикутник. Знайдіть тангенс гострого кута. Порівняйте результат з результатом сусіда.

1.          Накресліть рівносторонній трикутник. Проведіть у ньому висоту. Знайдіть синус і косинус кута а) 60⁰;б) 30⁰. Порівняйте результат з результатом сусіда.

Урок №42

Тема уроку

Співвідношення між сторонами і кутами в прямокутному трикутнику

Мета уроку

       Домогтися засвоєння учнями правил знаходження невідомих сторін прямокутного трикутника, що випливають з означень тригонометричних функцій гострого кута.

       Формувати вміння відтворювати зміст цих правил, а також застосовувати правила для знаходження невідомих сторін прямокутного трикутника.

        Закріплювати знання числових значень тригонометричних функцій кутів 30⁰, 45⁰, 60⁰ , знання вивчених формул та розвивати навички їх застосування.

       Виховувати наполегливість у здобутті знань .

Прийом  І

Проблемна ситуація

       Втомленим прийшов чужинець з півночі в країну Великого Хапи.  Сонце вже сідало, коли він підійшов до палацу фараона, щось сказав слугам. Ті миттєво розчинили перед ним двері й провели його до приймальної зали. І ось він стоїть у запиленому дорожньому плащі, а перед ним на золоченому троні сидить фараон. Поруч стоять пихаті жерці, хранителі вічних таємниць природи.

•  Хто ти ? - запитав верховний жрець.
• Звати мене Фалес. Родом я із Мілета.

Жрець пихато продовжував:

• Так це ти вихвалявся, що зможеш виміряти висоту піраміди, не піднімаючись на неї ? – жерці скорчились від реготу. – Добре буде, - продовжував жрець, - якщо ти помилишся не більше ніж на сто ліктів.
• Я можу виміряти висоту піраміди і помилитись не більше ніж на півліктя. Я зроблю це завтра.

Обличчя жерців потемніли.  Яке зухвальство! Цей чужинець стверджує, що може зробити те, чого не можуть вони – жерці Великого Єгипту.

• Добре, - сказав фараон. – Біля палацу стоїть піраміда, ми знаємо її висоту. Завтра перевіримо твою майстерність.

(Учитель пропонує учням знайти спосіб вимірювання висоти  піраміди.)

Відповідь:    Він став під проміння сонця і виміряв довжину своєї тіні. Скажімо, тінь була в двічі довшою за зріст Фалеса. З цього Фалес зробив висновок, що в цю мить предмети мають тіні вдвічі більші за них самих. Тож залишається обчислити довжину тіні піраміди Хеопса.

Жерці були обурені від цієї винахідливості Фалеса. Те, що, на їх думку , людині взагалі не дано пізнати, якийсь там грек з Мілета обчислив майже миттєво.

Урок № 43

Тема уроку

Розв’язування прямокутних трикутників.

Мета уроку

       Працювати над засвоєнням учнями змісту поняття «розв’язати трикутник» та схем розв’язання чотирьох основних задач на знаходження сторін прямокутного трикутника. Сформувати вміння відтворювати зміст вивчених схем, а також застосовувати їх до розв’язування прямокутних трикутників.

      Розвивати логічне мислення та культуру математичних обрахунків.                       Виховувати відповідальність та наполегливість.

Прийом  І

Практична задача

1.Тінь від стовпа заввишки 11 м становить 4,4 м. Виразіть у градусах висоту Сонця над горизонтом.

Відповідь: 13⁰

Урок № 44

Тема уроку

Розв’язування задач.

Мета уроку

       Закріпити та систематизувати знання учнів про вивчені співвідношення між сторонами і кутами в прямокутному трикутнику.

      Розвивати навички застосовувати набуті знання для розв’язування прямокутних трикутників та задач на знаходження елементів інших фігур.

      Виховувати наполегливість та відповідальність.

Прийом  І

Практична задача

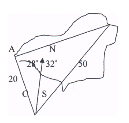
           Знайти ширину водоймища між точками, одна з яких знаходиться на відстані 20 м від нашого місцезнаходження і відхилена на захід на 32 °, а друга — відхилена схід кут 28 ° і знаходиться на відстані 50 м від нас.

Розв'язання

Проведено висоту AD; AD BC.

∆АDC:D=90°,DC=AC·cos60°=10(м)
AD =AC·sin60°=:2 = (м).

За аксіомою планіметрії :ВС= BD + CD,

тому BD = ВС - CD = 40(м).

∆ABD:  D= 90°. За теоремою Піфагора:

АВ² = AD² + BD² = 300 +1600 = 1900; АВ = 10 (м)

Відповідь: 10 м

Урок № 45

Тема уроку

Підсумковий урок.

Мета уроку

      Закріпити та систематизувати знання учнів про вивчені співвідношення між сторонами і кутами в прямокутному трикутнику.

      Розвивати навички застосовувати набуті знання для розв’язування прямокутних трикутників та задач на знаходження елементів інших фігур.

      Виховувати наполегливість та відповідальність.

Прийом  І

Практична задача

        Вершину дерева, віддаленого від даного пункту на 16 м, видно під кутом 16⁰ до горизонту , а вершину другого дерева віддаленого від цього самого пункту на 24 м, видно під кутом 19⁰. Яке дерево  вище і на скільки?

                                                   Розв’язання :

                                                        Дано: АС = 24 м, КС =16 м,

                                                     <α=16⁰,   <β=19⁰. 

                                Знайти: АВ-КМ.

АВ = АС β,    КМ = КС α.  АВ = 24 · 0,344=8,256 м,

  КМ = 16 · 0,287 = 4,592 м.    АВ – КМ = 3,664 м.

Відповідь: 3,664 м.

Урок № 46

Тема уроку

Контрольна робота №5.

Мета уроку

      Перевірити якість засвоєння учнями знань щодо змісту основних понять теми, перевірити якість сформованих знань щодо застосування набутих знань для виконання зображення фігур за умовою задачі, а також для розв’язання стандартних  і нестандартних задач .

    Розвивати логічне мислення і математичну пам'ять.

     Виховувати культуру математичних записів.

Прийом  І

Цікава задача для домашнього завдання

Давньокитайська задача про лотос.

Над озером тихим

Висотою з півфута підіймалась лотоса квітка,

Яка росла одиноко.

Та вітер скаженим поривом

Відніс її вбік.

І не стало видно квітки над водою.

Знайшов же її тільки рибалка ранньою весною

В двох футах від місця, де вона росла,

Яка в цьому місці на озері води глибина?

Розв’язання

Дано: ВМ = 2 фута, АВ = 0,5 фута, АС = СМ.

Знайти ВС.

Розв'язання

           Нехай ВС = х, тоді АС = СМ = х + 0,5. За теоремою Піфагора в ∆ СВМ  (⁰)  маємо: СМ² = ВС² + ВМ² ; (х + 0,5)² = х² + 2²; 

х² + х + 0,25 = х² + 4;    х = 4 – 0,25;   х = 3,75.

Відповідь. 3,75 фута.

Розділ ІУ

Многокутники. Площа многокутника.

Урок № 47

Тема уроку

Многокутники

Мета уроку

      Сформувати в учнів поняття: про ламану , її елементи  і  довжину; про многокутник, його елементи і периметр; про вписаний у коло многокутник і описаний навколо кола.

      Розвивати вміння знаходити довжину ламаної та периметр многокутника, виконувати  точне і схематичне зображення цих фігур, застосовувати зміст вивчених понять при розв’язуванні простіших задач.

     Виховувати охайність і спостережливість.

Прийом  І

Міні – лекція

        Ми починає вивчати наступний розділ «Многокутники . Площі многокутників.», в якому узагальнимо і доповнимо знання про многокутники , їх кути та площі. Завдяки цьому ви поповните свій багаж знань чималою кількістю нових формул, які необхідно знати і вміти застосовувати. Дам вам пораду : запам’ятати будь-яку формулу значно простіше, якщо зрозуміти і запам’ятати спосіб її отримання.

Прийом  ІІ

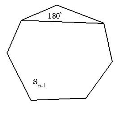
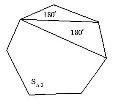
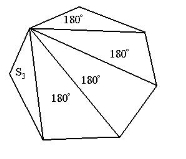
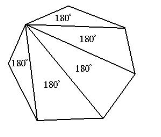
Проблемна ситуація

1.    Накресліть опуклий шестикутник.

а) Проведіть червоним кольором діагональ, яка ділить даний шестикутник на два чотирикутники. Скільки існує таких діагоналей?

б) Проведіть синім кольором діагональ, яка ділить даний шестикутник на трикутник і п'ятикутник. Встановіть закономірність між кількістю кутів опуклого многокутника і сумарною кількістю кутів многокутників, на які він ділиться діагоналлю.

2.    Периметр опуклого многокутника дорівнює 20 см  Чи може його діагональ дорівнювати 10 см? Відповідь поясніть

Прийом  ІІІ

Виховний момент

Чи знають бджоли математику?

        Учені, які досліджували бджолині стільники, переконалися: всі кути, що утворює шестикутник бджолиної чарунки, саме такі, для яких чарунка найбільш містка і при цьому на неї йде найменше воску. Начебто бджоли, будуючи свої стільники, користуються складними математичними обчисленнями. Побудовані ними без усяких креслень стільники з найбільшою точністю відтворюють розміри ідеальної споруди, розрахованої за всіма правилами науки. Так що це таке? Знання математики?...

      ( Відповідь . Учені дійшли висновку, що це ні що інше , як вироблений у процесі еволюції інстинкт. Інстинкт – природна здатність виконувати необхідні для життя дії. Бджоли, не знаючи математики , « визначили» , що правильний шестикутник має найменший периметр порівняно з периметрами правильних трикутників і квадратів. Будуючи шестикутні чарунки, бджоли витрачають менше воску на їх побудову й ощадливо використовують площу всередині невеликого вулика).

       Отже, головне, що відрізняє людину, яка приймає рішення, від істоти, яка живе інстинктами, це розум, здатність мислити і творити без шпаргалки.

Урок № 48

Тема уроку

Сума кутів опуклого многокутника.

Мета уроку

       Закріпити знання змісту понять, вивчених на попередньому уроці. Домагатись засвоєння учнями змісту та доведення теорем и про суму кутів опуклого многокутника. Формувати вміння відтворювати зміст вивченої теореми, навички застосування теореми під час розв’язування задач на знаходження градусної міри кутів многокутника.

       Розвивати логічне мислення і математичну пам'ять.

       Виховувати культуру письма і мовлення.

Прийом  І

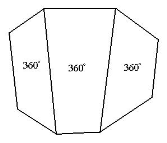
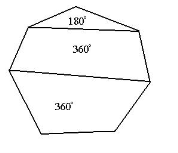
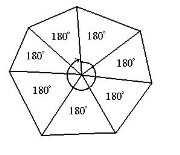
Логічна вправа

Які  числа  пропущено? (рис 1.)

а)                                        б)                                 в)

            180                                       360     

               г)

 Рис 1.

Прийом  ІІ

 Свято думок

Теорема. Сума кутів опуклого п-кутника дорівнює 180°(п-2)

І спосіб доведення.

1-й крок. n - кутник розбивається діагоналлю, що виходить з вершини, на трикутник і n -1-кутник.

 Тоді сума кутів n - кутника S_n=180° + S_n-1, де S_n-1 – сума кутів n -кутника.

2-й крок. Знаходимо S_n-1, розбиваючи n -1-кутник другою діагоналлю, що виходить із тієї ж вершини многокутника, на трикутник і n -2-кутник.

 Тоді

S_n-1= 180° + S_n-2,

S_n =  180° + (180° + S_n-2),

S_n =  180°·2 + S_n-2.

      І так розбиваємо n - кутник доти, доки останній із многокутників n -3-ю діагоналлю не буде розбитий на n -2 трикутники:

S_n = 180°(n-3)+S3;

S_n = 180°(n-3)+180°;

S_n = 180°(n-2).

ІІ спосіб доведення.

Якщо n – кількість сторін многокутника, то n -2 – кількість утворених трикутників діагоналями, що виходять з однієї вершини.

Сума кутів даного многокутника дорівнює сумі усіх цих трикутників:

S_n = 180°(n-2).

ІІІ спосіб доведення.

1. Нехай в опуклому n - кутнику парна кількість сторін. Розіб’ємо його діагоналями на чотирикутники.

 - кількість утворених чотирикутників. Сума кутів даного п-кутника дорівнює сумі цих чотирикутників:

S_n = 360°,

S_n = 180°(n-2).

2. Нехай в опуклому n - кутнику непарна кількість сторін. Розіб’ємо його діагоналями на  чотирикутники та один трикутник.

Сума кутів даного n - кутника дорівнює сумі кутів усіх чотирикутників та кутів трикутника:

Sn = 360°· + 180°,

Sn = 180°(n-2).

VІ спосіб доведення.

Виберемо довільну внутрішню точку опуклого n - кутника і з’єднаємо її з усіма вершинами.

Отримаємо n трикутників зі спільною вершиною у точці О. Сума всіх кутів при вершині - 360°. Сума кутів усіх трикутників 180°× n. Тоді 180° n = S_n + 360°, де S_n – сума кутів n -кутника. Отже,

S_n = 180° n -360°,

S_n = 180°(n-2).

Урок № 49

Тема уроку

Поняття площі многокутника.

Мета уроку

      Сформувати в учнів поняття про площу многокутника, одиницю вимірювання площ, властивості (аксіоми) площ, рівновеликі фігури, рівно складені многокутники, властивість рівно складених многокутників та оберненого твердження; працювати над засвоєнням учнями ідеї доведення теореми про площі прямокутника і квадрата. Формувати вміння застосовувати теореми для обчислення площ прямокутника і квадрата.

      Розвивати логічне мислення.

      Виховувати самостійність і наполегливість у навчанні.

Прийом  І

Історична довідка

         Давні вавилоняни ще чотири тисячі років тому вміли правильно обчислювати площу квадрата, прямокутника, трапеції. Чимало формул площ і об’ємів, з якими ви познайомитесь в старших класах, відкрив знаменитий грецький учений Архімед (близько 287-212 рр. до н. е.). і все при тому, що в давні часи не було алгебраїчної символіки.

         Пропоную учням на наступний урок зробити невеликі сповіщення у вигляді реферату, усного виступу, мульти – недійної презентації, відеоролика про Архімеда.

Урок № 50

Тема уроку

Площа прямокутника. Площа паралелограма.

Мета уроку

      Закріпити знання учнів змісту та властивостей площі многокутника, змісту  теореми про площу прямокутника та його наслідок. Сформувати та довести теорему про площу паралелограма.

     Розвивати вміння відтворювати зміст вивчених понять та теорем, а також використання їх під час розв’язування задач на обчислення площ прямокутника і паралелограма.

     Виховувати культуру математичних записів.

Прийом  І

Ігровий момент

 Учитель тримає в руках каркасну модель прямокутника. З’ясувавши в учнів , що це за фігура, він починає повільно «зсувати» верхню основу відповідно до нижньої. Яким має бути гострий у другого чотирикутника, щоб його площа була в двічі нижчою від площі прямокутника?

Прийом  ІІ

«Мозковий штурм»

        1)Потрібно побудувати три прямокутника і три паралелограма площа кожного з яких дорівнює 12см² .

        2)Дано два квадрати. Потрібно за допомогою циркуля і лінійки без поділок побудувати квадрат, площа якого дорівнює сумі площ даних квадратів.

       3) Побудувати прямокутник площею 36 см² і рівновеликий йому квадрат.

4) Чи можна висадити 1500 саджанців яблуні на земельній ділянці прямокутної форми з розмірами 20 м і 40 м, якщо на одну сотку можна висадити до 20 саджанців

Прийом  ІІІ

Практична задача

 Територія лісу на карті масштабу 1:100 000 має форму прямокутника із сторонами 42 мм і 57 мм. Визначте площу лісу в гектарах.

Розв'язання

       Площа прямокутника (S) визначається за формулою:

 S = ab , де a, b - сторони прямокутника.

1. визначаємо площу лісу на карті: S = 4,2 см х 5,7 см =

23,94 см ²;

 2) переводимо числовий масштаб карти в іменований: в 1 см - 1 000 м;

 3) визначаємо, чому дорівнює 1 см ² на місцевості: 1 см ²= 1 000 м х 1 000 м = 1 000 000 м²;

 4) визначаємо площу лісу на місцевості: 1 000 000 м² х 23,94 = 23 940 000 м²;

 5) переводимо м у га (1 га = 10 000 м²):

 23 940 000 м² : 10 000 м² = 2 394 га.

 Відповідь: площа лісу 2 394 га.

Урок № 51

Тема уроку

Розв’язування задач.

Мета уроку

      Закріпити та систематизувати знання учнів про зміст поняття площі многокутника та його властивості , про формули для обчислення площ прямокутника і паралелограма.

     Розвивати вміння і навички застосовувати здобуті знання.

     Виховувати самостійність і наполегливість у навчанні.

Прийом  І

Практична екологічна задача

       1 га соснового лісу 20-річного віку поглинає за рік 9350 кг вуглекислого газу і виділяє 7250 кг кисню. Скільки вуглекислого газу поглине і скільки кисню виділить невеликий сосновий ліс біля села Станіславчик , який має форму прямокутника з розмірами 1250 м на 200м ?

Прийом  ІІ

Практична задача

       Визначте площу фруктового саду, якщо на плані масштабу 1 : 5 000 він має форму квадрата, діагональ якого на цьому плані дорівнює 12 см.

Розв'язання:

 площа квадрата (S) визначається за формулою:

 S = а² =1/2 d², де а - сторони квадрата, d - діагональ.

 1) Визначаємо площу саду на плані:

 S=1/2∙12²=72cм²

 2) числовий масштаб карти: 1 см = 50 м;

 3) визначаємо, чому дорівнює 1 см ² на місцевості:

 1см²=50м х 50м = 2 500 м²;

 4) визначаємо площу саду на місцевості:

 2 500 м² х 72 = 180 000 м²;

 5) переводимо м² у га (1 га = 10 000 м²):

 180 000 м² : 10 000 м² = 18 га.

 Відповідь: площа саду 18 га.

Урок № 52

Тема уроку

Площа трикутника.

Мета уроку

     Домогтися засвоєння учнями змісту та ідеї доведення теореми про площу трикутника та наслідків з неї. Сформувати вміння відтворювати зміст вивчених формул та вміння записувати їх відповідно до заданих позначень елементів трикутників.

     Розвивати навички застосування формул до розв’язування задач та креативність при досягненні результату.

      Виховувати бажання здобувати знання.

Прийом  І

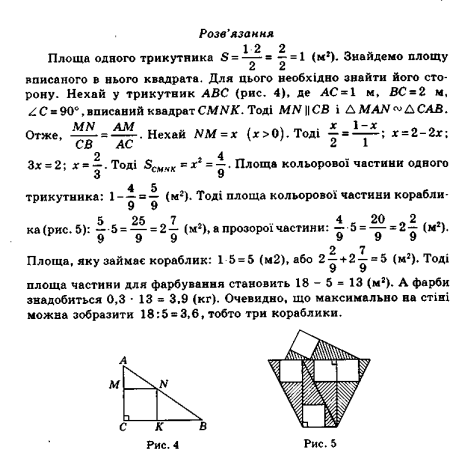
Проблемна задача

        Шкільний коридор вирішили викласти керамічною плиткою, кожна з яких має форму рівнобедреного прямокутного трикутника з катетом 60см . Плитка є двох кольорів - синя і блакитна . скільки плитки кожного кольору потрібно закупити, якщо їх використовують порівну, а площа коридору 175м² ?

Розв’язання

1.             Площа однієї плитки – це площа половини квадрата зі

            стороною 60см, вона дорівнює 0,5 · (60·60) =1800 (см² ).

2.             Площа двох плиток різного кольору дорівнює

           2·1800=3600(см² ) = 0,36(м² ).

3. Потрібно 175(м² ): 0,36(м² ) = 486,1≈487 плиток кожного кольору.

Відповідь: 487 плиток кожного кольору.

Прийом  ІІ

Лабораторна робота

Кожен учень отримує модель (моделі пронумеровані), робить необхідні вимірювання і обчислення, дані заносить в таблицю:

Прийом  ІІІ

Практична задача

1.  Визначте площу ріллі, якщо на плані масштабу 1 : 5 000 вона має форму прямокутного трикутника, один з катетів якого дорівнює 50 мм, а другий - 48 мм.

Розв'язання

 Площа прямокутного трикутника (S) визначається за формулою:

 S =ab, де а,b - катети.

 1) Визначаємо площу ріллі на плані: S = 5см х 4,8 см = 12 см ;

 2) числовий масштаб карти: в 1 см - 50 м;

 3) визначаємо, чому дорівнює 1 см ² на місцевості:

 1 см²=50м х 50 м = 2 500 м²;

 4) визначаємо площу саду на місцевості:

 2 500 м² х 12 = 30 000 м²;

 5) переводимо м² у га (1 га = 10 000 м²):

 30 000 м² : 10 000 м² = 3 га.

 Відповідь: площа ріллі 3 га.

2. Визначте площу городу, якщо на плані масштабу 1:2 ООО він має форму прямокутного трикутника, один з катетів якого дорівнює 4 см, а гіпотенуза - 5 см.

Розв'язання

 Площа прямокутного трикутника (S) визначається за формулою:

 S = 1/ab, де а,b - катети.

1.  Для того щоб визначити довжину другого катета, використовуємо теорему Піфагора. За теоремою Піфагора, у трикутника АВС кут С дорівнює  90°;

 АВ²=АС²+ВС²

 b = АС = ,

 b = АС = ===3см.

2.  Використовуючи формулу, визначаємо площу городу на

 плані:

 S = 1/2 х 4см х З см = 6см²;

3. Переводимо числовий масштаб плану в іменований:

1 см = 20 м;

4) Визначаємо, чому дорівнює 1 см ² на місцевості:

1см ² = 20мх20м = 400 м²;

5)Визначаємо площу городу на місцевості:

400.  х 6 = 2 400 м²;

6) Переводимо м² у га (1 га = 10 000 м²):

       2 400 м² : 10 000 м² - 0,24 га.

Відповідь: площа городу 0,24 га.

Урок № 53

Тема уроку

Площа трапеції.

Мета уроку

     Закріпити знання учнями формул для обчислення площі трикутника. Формувати знання формули площі трапеції та розуміння  її  доведення.

     Розвивати навички застосування формул до розв’язування задач та креативність при досягненні результату.

      Виховувати самостійність і зосередженість.

Прийом  І

Практична задача

           Визначте площу ріллі, якщо на плані масштабу 1:5 000 вона має форму трапеції з верхньою основою 23,6 мм; нижньою - 39,7 мм; висотою 14 мм.

Розв'язання

    Площа трапеції (S) визначається за формулою:

 S =(a-b)/2·h , де a, b - основи; h - висота.

1. Визначаємо площу ріллі на плані:

S=(2,36см-3,97см)/2х1,4см=4,431см²

2. переводимо числовий масштаб плану в іменований:

1 см = 50 м;

 3) визначаємо, чому дорівнює 1 см ² на місцевості:

      1 см ² = 50 м х 50 м = 2 500 м²;

 4) визначаємо площу ріллі на місцевості:

      2 500 м² х 4,431 = 11077,5 м²;

 5) переводимо м² у га (1 га = 10 000 м²):

     11077,5 м²:10000м²=1,11га.

 Відповідь: площа ріллі 1,11 га.

Прийом  ІІ

А це правда?

   Якщо трапеція рівнобічна, і в неї діагоналі перпендикулярні, то площа такої трапеції дорівнює  квадрату її висоти: S = h² .

Урок № 54

Тема уроку

Розв’язування задач.

Мета уроку

       Узагальнити та систематизувати знання формул обчислення площ трикутника й трапеції , наслідків.

       Розвинути навички застосування здобутих знань.

       Провести діагностику рівня засвоєння учнями навчального матеріалу.

        Виховувати спостережливість і уважність.

Прийом  І

Практичне завдання додому

          Стіна кафе має форму прямокутника зі сторонами 3 м і 6м. На стіні зображено морський пейзаж, що має мозаїчні вкраплення у вигляді кораблика, утвореного із з п'яти рівних прямокутних трикутників, у які вписано квадрати. Катети трикутника дорівнюють 1 м і 2 м. Квадрати складаються із прозорого скла, інша частина — з кольорового. Скільки квадратних метрів прозорого та кольорового скла потрібно для того, щоб викласти кораблик? Якою є площа частини стіни, що залишилася без мозаїки? Скільки фарби необхідно для того, щоб пофарбувати цю частину стіни, якщо для фарбування 1 м2 необхідно 300 г фарби? Яку мак­симальну кількість корабликів можна зобразити на стіні кафе?

Прийом  ІІ

Практична задача

 Визначте площу луків, якщо на карті масштабу 1:50 000 вони мають форму трикутника з основою 22,7 мм і висотою 15,4 мм.

Розв'язання

   Площа трикутника (S) визначається за формулою:

 S = 1/2 ah або S = 1/2absinα, де а - основа; Н - висота; a, b - сторони: α - кут між а і b.

 1) Використовуючи формулу, визначаємо площу луків на карті:

 S =1/2 х 2,27см х1,54 см = 1,7479 см ²

 2) переводимо числовий масштаб карти в іменований: 1 см = 500 м;

 3) визначаємо, чому дорівнює 1 см ² на місцевості:

 1 см ² = 500 м х 500 м = 250 000 м²;

 4) визначаємо площу луків на місцевості:

 250 000 м х 1 7479 = 436975 м ;

 5) переводимо м² у га (1 га = 10 000 м ):

 436 975 м²: 10 000 м² = 43,6975 га.

 Відповідь: площа луків 43,6975 га.

Прийом  ІІІ

 Виконання усних вправ

           Кожна будівельна  фірма повинна вміти швидко орієнтуватися в ситуації (перевіряється вміння застосовувати формули для розв'язування найпростіших задач).

1. Скільки потрібно взяти плит квадратної форми з діагоналлю 0,5 м, щоб покрити ними двір площею 200 м²?

(Відповідь: 800 штук.)

 2. Готельний хол має форму трапеції з основами 20 м і 10 м і висотою 8 м. Знайдіть площу ковроліна, необхідного, щоб застелити цей хол.

(Відповідь: 120 м².)

 3. Необхідно розбити у дворі три однакові клумби, кожна з яких має форму рівностороннього трикутника. Висота кожного трикутника дорівнює 3 м. Яку площу займуть ці клумби?

(Відповідь: 27 м².)

 4. Басейн має форму ромба. Довжина його діагоналей дорівнює 20 м і 16 м. Яку площу займе цей басейн?

(Відповідь: 160 м².)

 5. Дискотеки проводитимуть на площадці, що має форму шестикутника, у якого рівні всі сторони й кути. Визначте градусну міру кожного кута цього шестикутника й площу танцювального залу, враховуючи те, що місце для танців — коло, вписане в цей шестикутник, радіус кола дорівнює 5 м, а сторона шестикутника 20 м.

(Відповідь: 300 м².)

Урок № 55

Тема уроку

Відношення площ подібних фігур.

Мета уроку

   Домогтися засвоєння учнями змісту та ідеї доведення теореми про відношення площ подібних трикутників. Сформувати вміння відтворювати зміст теореми та застосовувати її під час розв’язування задач.

     Розвивати логічне мислення та культуру математичного мовлення.

     Виховувати спостережливість та уважність.

Прийом  І

Практична задача

1. Сторони двох правильних шестикутників відносяться, як 3:4. Як відносяться їх площі?

Розв’язання

 Оскільки правильні шестикутники подібні, то можна використовувати теорему про площі подібних многокутників. Отже, відношення площ шестикутників дорівнює

2. Площі двох подібних многокутників відносяться, як 9:16. Як відносяться периметри цих многокутників?

Розв’язання

1) Нехай а₁ і а₂ - відповідні лінійні розміри многокутників. Тоді

2) Оскільки периметри подібних многокутників, відносяться як відповідні сторони цих многокутників, то відношення периметрів многокутників також 3:4.

Відповідь: 3:4

3. Площа земельної ділянки на карті дорівнює 2,8 см², а масштаб карти 1:10000. Яка справжня площа земельної ділянки?

Розв’язання

1) Нехай S см² - площа ділянки.

2)Оскільки масштаб є коефіцієнтом подібності карти по відношенню до земельної ділянки, тоді

Оскільки

  Відповідь:28000 м²

Урок № 56

Тема уроку

Метод площ. Розв’язування задач.

Мета уроку

     Закріпити, систематизувати та узагальнити знання учнів з теми : «Площі многокутників». Сформувати в учнів розуміння схеми дій, що відповідають змісту поняття «метод площ».

    Провести діагностику рівня засвоєння учнями навчального матеріалу розділу ІІІ.

      Розвивати алгоритмічне мислення.

      Виховувати відповідальність.

Прийом  І

Усні вправи

2. Визначити, як зміниться площа трикутника, якщо кожну його сторону :

а) збільшити в 2 рази;

б)зменшити  в 3 рази ?

2) Визначте , як треба змінити кожну сторону трикутника ,

 щоб його площа :

       а) зменшилася у 25 разів;

       б)збільшилася у 49 разів ?

Прийом  ІІ

Графічна вправа

    Накресліть прямокутний трикутник, проведіть  в ньому середню лінію, паралельну одному з катетів.

    а) Виміряйте катети даного трикутника й обчисліть його площу.

    б) Користуючись теоремою про площі подібних трикутників, обчисліть площу трикутника, який відтинається від даного середньою лінією.

    в) Обчисліть площу трикутника, який відтинається від даного середньою лінією, вимірявши його гіпотенузу і висоту.

    Порівняй отримані результати.

Урок № 57

Тема уроку

Підсумковий урок.

Мета уроку

     Повторити, систематизувати та узагальнити знання учнів щодо змісту поняття площі многокутника та її властивостей, формул для обчислення площ чотирикутників та трикутника, а також властивостей площ подібних трикутників.

      Розвивати уміння учнів застосовувати набуті знання для розв’язування задач на обчислення площ чотирикутників та трикутників.

      Виховувати  самостійність та наполегливість.

Прийом  І

 Міні – лекція

          На попередніх уроках ми з вами обчислювали площі многокутників, навчилися розв’язувати задачі. Отже, тема нашого сьогоднішнього уроку Розв’язування задач на обчислення площ многокутників. Мета уроку: узагальнити та систематизувати знання учнів про площі многокутників ;

формувати вміння учнів застосовувати теорему про площу прямокутника. трикутника, паралелограма, трапеції при розв’язанні задач.

Проведемо даний урок у вигляді аукціону. Аукціон – це розпродаж цінностей. Найбільша наша цінність - це знання.

Вчитись легко буває,

Та наука завжди хороша

Кожна в світі людина знає,

Що знання – то найлегша,

Найцінніша ноша.

Прийом  ІІ

Задачі практичного змісту для домашнього завдання

1. Треба обгородити квадратну ділянку землі зі стороною 25 м або прямокутну ділянку, що її довжина на кілька метрів більша, а ширина на стільки ж метрів менша від сторони квадрата. Порівняйте площі і периметри квадрата та прямокутника.
2. Щоб обгородити дитячий майданчик прямокутної форми, виготовили 120 щитів довжиною 3 м кожний. Якої довжини мають бути сторони прямокутника, щоб площа майданчика була найбільшою?

Урок № 58

Тема уроку

Контрольна робота №4.

Мета уроку

     Перевірити якість засвоєння учнями змісту поняття площі многокутника та її властивостей, формул для обчислення площ чотирикутників та трикутника, а також властивостей площ подібних трикутників.

    Здійснити контроль сформованих в учнів умінь щодо застосування вивчених тверджень для розв’язування задач на обчислення площ чотирикутників та трикутника, а також властивостей площ подібних трикутників, а також для розв’язування задач методом площ.

     Розвинути навички застосування здобутих знань.

     Виховувати відповідальність.

Прийом  І

Історична довідка

   Обчислення площ многокутника є першою серед тих практичних задач, яким геометрія як наука завдячує своєю появою. Однак не завжди уявлення про вимірювання площ було таки, як воно є сьогодні.

     Наприклад стародавні єгиптяни брали за площу будь-якого трикутника половину добутку двох його сторін. Так само площу трикутника вимірювали і в Давній Русі. Для площі чотирикутника , який не є квадратом, у Вавилоні використовували формулу добутку півсум його протилежних сторін.

   Сьогодні , володіючи значно ширшими можливостями застосування алгебри в геометрії, в багатьох задачах ми маємо змогу дата більш прості й зрозумілі розв’язання , ніж це було можливо  в давнину.

Розділ ІІІ

Розв’язування прямокутних трикутників

Урок № 59

Тема уроку

Синус, косинус і тангенс гострого кута прямокутного трикутника.

Мета уроку

     Домогтися розуміння і засвоєння учнями змісту означень синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей , що випливають з теореми Піфагора, подібності прямокутних трикутників та властивостей прямокутного трикутника( проти більшої сторони лежить більший кут і навпаки).

     Сформувати вміння відтворювати зміст означень та їх властивостей, а також знаходити значення тригонометричних функцій гострого кута за допомогою прямокутного трикутника.

     Розвивати абстрактне логічне мислення.

     Виховувати цікавість до вивчення математики.

Прийом  І

Практична задача

   Із точки на землі верхівку дерева видно під кутом 50°,  а людину, що перебуває під цим деревом, — під кутом 15° . Знайдіть висоту дерева, якщо зріст людини дорівнює 180 см.

Урок № 60

Тема уроку

Тригонометричні тотожності.

Мета уроку

     Удосконалити вміння застосовувати співвідношення між сторонами і кутами прямокутного трикутника до розв’язування задач.

  Розвивати логічне абстрактне мислення. Виховувати цікавить до математики.

Прийом  І

Проблемна задача.

 Зі спостережного пункту на землі літак, що пролітає над вежею, видно під кутом 65° . З того ж спостережного пункту верхню точку вежі видно під кутом 30°. На якій висоті летить літак, якщо висота вежі дорівнює 80 м?

Розв’язання

Відстань від спостережного пункту до вежі : 8030⁰=136(м)

Відстань від землі до літака : 13665⁰ = 292,4 (м)

Відповідь: 292,4 (м)

Урок № 61

Тема уроку

Розв’язування задач.

Мета уроку

     Узагальнити та систематизувати знання учнів про означення тригонометричних функцій гострого кута , їх основні властивості, а також про способи застосування набутих знань при розв’язуванні вправ.

     Розвивати логічне абстрактне  мислення .

     Виховувати відповідальність та колективізм.

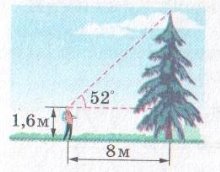
Прийом  І

Практична задача

За рисунком знайдіть висоту ялинки

      Розв’язання

1,6+852⁰=1,6+8 1,28=11,84(м)

   Відповідь: 11,84 м           

Урок № 62

Тема уроку

Підсумковий урок.

Мета уроку

    Повторити, систематизувати та узагальнити знання учнів щодо співвідношень між сторонами у кутами в прямокутному трикутників.

      Розвивати уміння учнів застосовувати набуті знання для розв’язування задач на обчислення сторін і кутів прямокутного трикутника

      Виховувати  самостійність та наполегливість.

Прийом  І

Прикладна задача

На вершину гори висотою 2400 м можна дістатись за допомогою фунікулера . Під яким кутом до поверхні землі розташована траса фунікулера , якщо швидкість його руху становить 16 км/год. , а час підйому – 18 хв. ?

Урок № 63

Тема уроку

Контрольна робота №5.

Мета уроку

     Перевірити якість засвоєння учнями означень тригонометричний функцій гострого кута прямокутного трикутника, таблички значень цих функцій для кутів 30⁰, 45⁰, 60⁰. 

    Здійснити контроль сформованих в учнів умінь щодо застосування вивчених тверджень для розв’язування задач на знаходження кутів і сторін прямокутного трикутника.

     Розвинути навички застосування здобутих знань.

     Виховувати відповідальність і самостійність..

Прийом  І

Розділ ІУ

Повторення і систематизація

навчального матеріалу.

Урок № 64

Тема уроку

Паралелограм, прямокутник, ромб, квадрат, властивості, обчислення площ.

Мета уроку

   Повторити ,систематизувати та узагальнити знання учнів про означення, ознаки та властивості паралелограмів і способи обчислення їх площ.

   Розвивати вміння і навички застосування знань до розв’язування задач .

   Виховувати бажання вивчати математику.

Прийом  І

Практична задача

     Визначте площу поля, якщо на плані масштабу 1:5 000 воно має форму ромба з діагоналями 12 см і 8 см.

Розв'язання

   Площа ромба (S) визначається за формулою: S=d₁d₂, де d₁d₂ – діагоналі.

 1) За формулою визначаємо площу поля на плані:

 S = 12 см х 8 см = 96 см ²;

 2) переводимо числовий масштаб плану в іменований:

 1 см = 50 м;

 3) визначаємо, чому дорівнює 1 см ² на місцевості:

 1 см ²= 50 м х 50 м = 2 500 м²;

 4) визначаємо площу ріллі на місцевості:

 2 500 м² х 96 = 240 000 м²;

 5) переводимо м² у та (1 га = 10 000 м²):

 240 000 м²: 10 000 м² = 24 га.

 Відповідь: площа поля 24 га.

Урок № 65

Тема уроку

Трапеція: властивості, обчислення площі.

Мета уроку

   Повторити ,систематизувати та узагальнити знання учнів про означення, ознаки та властивості трапеції способи обчислення їх площ.

   Розвивати вміння і навички застосування знань до розв’язування задач .

   Виховувати наполегливість і спостережливість, вміння аналізувати та спів ставляти.

Прийом  І

Ігровий момент

1. Учитель: Я накреслив трапецію на аркуші паперу. Поставте лише одне запитання і , вислухавши відповідь, скажіть , чи буде вона рівнобічною?
2. Учитель: одного разу Вова Зазнайко побудував трапецію з чотирьох прямокутних трикутників. Чи можете ви повторити його досягнення? А «поліпшити» (тобто використати меншу кількість трикутників) ?

Урок № 66

Тема уроку

Площа трикутника.

Мета уроку

Повторити ,систематизувати та узагальнити знання учнів про способи обчислення площі трикутників.

   Розвивати вміння і навички застосування знань до розв’язування задач .

   Виховувати наполегливість і спостережливість, вміння аналізувати та спів ставляти  .

Прийом  І

Ігровий момент

        Учень отримав моделі трьох квадратів (рис . 1). Не користуючись жодними інструментами, доведіть, що площа одного з них дорівнює площі двох інших.

                                 Рис. 1

Прийом  ІІ

Проблемна ситуація

Яку частину площа заштрихованої фігури складає від площі трикутника( рис. 2)?

              а)                                   б)                                   в)

                                 рис. 2

Урок № 67

Тема уроку

Подібність трикутників та її застосування.

Мета уроку

Повторити ,систематизувати та узагальнити знання учнів про означення і  властивості подібності трикутників, ознаки подібності трикутників.

   Розвивати вміння і навички застосування знань до розв’язування задач .

   Виховувати наполегливість і спостережливість, вміння аналізувати та спів ставляти.

Прийом  І

Практична задача

В нашому місті є високі вишки і водонапірні башти. У вас є фотографія однієї з них і ви хочете знати її справжню висоту. Як ця фотографія може допомогти вам дізнатись її висоту?

Відповідь:  Щоб за фото дізнатись висоту башти , треба спочатку як можна точніше виміряти на фото

Прийом  ІІ

Математичний диктант

Урок № 68

Тема уроку

Прямокутний трикутник.

Мета уроку

Повторити ,систематизувати та узагальнити знання учнів про означення, властивості і ознаки подібності прямокутних трикутників, метричні співвідношення в прямокутному трикутнику, теорему Піфагора і схеми розв’язування прямокутних трикутників.

   Розвивати вміння і навички застосування знань до розв’язування задач .

   Виховувати наполегливість і спостережливість, вміння аналізувати та спів ставляти.

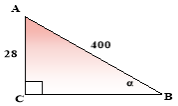
Прийом  І

Практична задача

1. Знайдіть кут підйому гірського шосе, якщо на відстані 400 м висота підйому становить 28 м.

                                    Дано:

                                                                             АС=28м; АВ=400 м

                                                                              Знайти: α

                                                 Розв’язування:

Відповідь: 4°

Урок № 69

Тема уроку

Контрольна робота №6.

Мета уроку

Перевірити якість засвоєння учнями знань щодо змісту основних понять геометрії ,вивчених у 8 класі, перевірити якість сформованих знань щодо застосування набутих знань для виконання зображення фігур за умовою задачі, а також для розв’язання стандартних  і нестандартних задач .

    Розвивати логічне мислення і математичну пам'ять.

     Виховувати культуру математичних записів.

Урок № 70

Тема уроку

Підсумковий урок.