Урок "Розв'язування задач по темі "Чотирикутники".

 

 

 

 

 

 

 

 

 

 

Підсумковий урок по темі:

„Чотирикутники.”

 

 

 

 

 

 

 

 

 

 

Тема.Розв’язування задач по темі «Чотирикутники»

Мета. Повторення, систематизація, корекція і більш глибоке осмислення учнями  навчального матеріалу по даній темі; розвивати логічне мислення учнів, шляхом постановки питань творчого характеру; формувати комунікативну культуру, утверджувати демократичні відносини, тактовність у стосунках учнів.

Тип уроку. Урок узагальнення і систематизації знань.

Обладнання. Креслярські інструменти, рисунки до задач, мультимедійний проектор, ноутбук.

 

ХІД УРОКУ.

І. Організація класу.

ІІ. Актуалізація опорних знань.

„Математика цікава  тільки тоді, коли дає поживу нашій винахідливості й здатності до міркувань» П.ПойаТРЕБА НЕ ТІЛЬКИ ОПАНОВУВАТИ МУДРІСТЬ, А Й УМІЛО КОРИСТУВАТИСЬ НЕЮ.” Ціцерон.

Ці слова видатного математика стануть девізом нашого уроку.

 

Урок проводиться у формі гри. Клас заздалегідь поділений на три групи – команди.

 

I конкурс (теоретична розминка).

Кожній команді роздається табличка, яку потрібно заповнити, записуючи в клітинці, що є перетином рядка і стовпця, ,,+”, якщо чотирикутник має відповідну властивість, і ,,-”, якщо ні.

Кожна правильна відповідь оцінюється 0,1 балa.

 

Вид чотирикутника Властивості	Парале лограм	Прямо кутник	Ромб	Квадрат	Трапеція
Протилежні сторони попарно паралельні
Всі кути рівні
Всі сторони рівні
Діагональ поділяє на 2 рівних трикутника
Протилежні сторони і кути рівні
Діагоналі в точці перетину діляться навпіл
Сума кутів прилеглих до однієї сторони, дорівнює 180˚
Діагоналі рівні
Діагоналі взаємно перпендикулярні
Діагоналі є бісектрисами кутів

 

 

 

 

 

 

Команди обмінюються табличками,  перевіряють відповіді суперників, звіряючи з відповідями, які висвітлюються на екрані.

 

II конкурс   Хто швидше? (теоретична розминка)

Які з діаграм Ейлера показують правильні співвідношення між множинами чотирикутників? Відповідь обгрунтувати.

Кожна правильна відповідь оцінюється 1 балом.

 

 

 

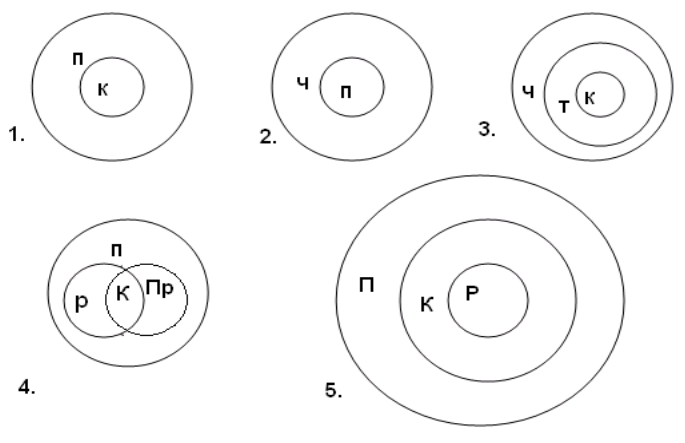
П – паралелограм; Пр – прямокутник;

Ч – чотирикутник; К – квадрат; Р – ромб;

Т - трапеція

 

III конкурс

Конкурс для капітанів команд. Потрібно дати  за 1хв найбільше правильних відповідей на запитання. Чи правильне твердження?- «так» чи «ні».  Кожна правильна відповідь оцінюється в 1 бал.

Запитання для капітана I команди.

1. Кожний квадрат є прямокутником.
2. У паралелограма всі кути рівні.
3. Існує квадрат, який є  ромбом.
4. У ромба всі кути рівні.
5. Сума протилежних кутів паралелограма дорівнює 180°
6. Якщо протилежні сторони чотирикутника рівні, то він – паралелограм
7. У прямокутника всі кути рівні
8. Діагоналі квадрата рівні
9. У паралелограма діагоналі є бісектрисами його кутів.
10. Кожний ромб є квадратом.

Запитання для капітана ІІ команди

1. Існує ромб, який є прямокутником.
2. Діагоналі паралелограма точкою перетину діляться навпіл
3. Діагоналі ромба є бісектрисами його кутів
4. Якщо діагоналі паралелограма рівні, то він прямокутник.
5. Якщо у чотирикутнику три кути рівні, то він  - прямокутник.
6. У прямокутника діагоналі точкою перетину не діляться навпіл.
7. Діагоналі ромба взаємно перпендикулярні.
8. Якщо діагоналі паралелограма взаємно перпендикулярні, то він- ромб.
9. Якщо діагоналі паралелограма є бісектрисами його кутів, то він ромб.
10.  У прямокутника всі сторони рівні.

Запитання для капітана III команди.

1. Жоден прямокутник не є ромбом.

2. У паралелограма сусідні сторони паралельні.

3. Ромб – це прямокутник із рівними сторонами.

4. Якщо  дві протилежні сторони чотирикутника рівні і паралельні, то він – паралелограм.

5. У паралелограма всі кути рівні.

6. Діагоналі паралелограма перпендикулярні.

7. У паралелограма всі сторони рівні.

8. Протилежні кути ромба рівні.

9. Діагональ прямокутника ділить його на два рівних трикутники.

10. У прямоутника всі сторони рівні.

 

 

 

 

 

 

 

 

 

IV конкурс

 

Задача на доведення. Конкурс оцінюється в 3 бали. Капітани вибирають завдання.

1 хвилина на обговорення.

     

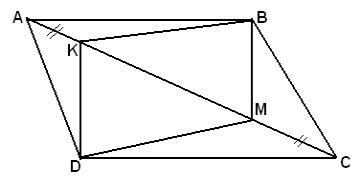
Дано:

ABCD – паралелограм; АК = СМ.

Довести:

DKBM - паралелограм

 

 

 

 

 

 

 

 

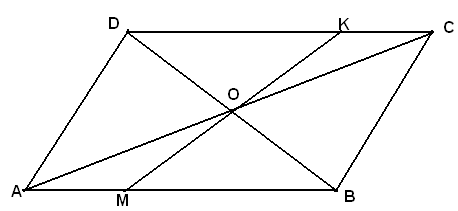
Дано:

ABCD – паралелограм.

Довести:

МО = OК

 

 

 

 

 

 

 

 

 

 

 

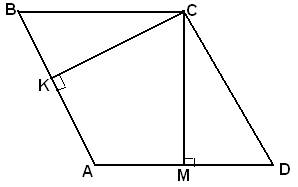
Дано:

ABCD – паралелограм, СМ = СК

Довести:

ABCD - ромб

 

 

V конкурс. Знайти невідомий елемент в трапеції. Оцінюється в 5 балів. Капітани команд вибирають завдання. (3 хв на обговорення).

 

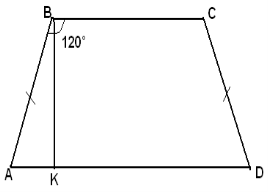К5.1

 Дано:

ABCD – рівнобчна трапеція,

 ВК – висота, АК = 4 см, КD = 16 см

Знайти:

периметр ABCD

 

 

 

 

 

К5.2

 

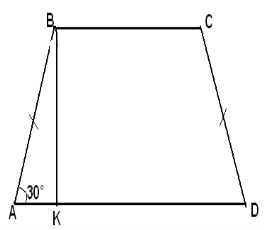
      Дано:

ABCD – рівнобчна трапеція, ВК – висота,

ВК = 4 см, МN -  середня лінія? NM=12 см

Знайти:

периметр ABCD

 

 

 

 

 

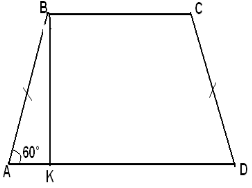К5.3

                                                                                      Дано:

ABCD – рівнобчна трапеція, ВК – висота,

АВ = 18 см, МN -  середня лінія,

 АD = 32 см

                                                                                                              Знайти: МN

 

 

 

 

 

 

 

 

 

 

 

 

VI конкурс.

Розв’язати кросворд.

Кожна команда отримує листок з надрукованим кросвордом. Команда яка розгадає швидше отримає 2бали.

 

 

 

 

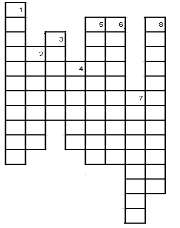
• 1. Паралелограм, у якого всі кути прямі.
•    2. Прямокутник, у якого всі сторони рівні
•                                   3. Паралельні сторони трапеції.
•                                 4.  Як поділяються діагоналі паралелограма точкою перетину?
• 5. Несусідні вершини чотирикутника
•                           6.   Промінь, що виходить з вершини кута і ділить його пополам.
•                          7. Відрізки, що сполучають протилежні вершини чотирикутника.
•   8. Відрізок, що сполучає середини сторін трапеції
•  

VII конкурс

Кожна з команд за даним малюнком повинна скласти задачу для своїх суперників. (На обговорення 3хв.) Капітани команд умови задач записують на дошці. На розв’язування задач кожній команді дається по 2хв. Конкурс оцінюється; за складену задачу -5 балів, а за розв’язок-3 бали.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

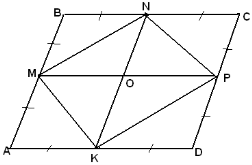
VIII конкурс.

Хто швидше?

Різні способи розв’язання задачі, 3б за кожне .

 

 

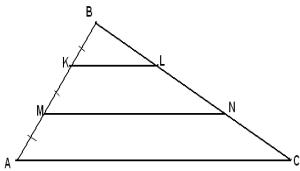
                                            Дано:

        АВС – трикутник, АМ = МК = КВ;

КL II MN II AB

MN- КL = 8см.

Знайти: АС

 

 

 

 

 

 

 

II  Підведення підсумків

• Капітани команд підраховують кількість отриманих балів
• Оцінюють роботу своїх гравців

Додатковий бал додається тій команді, чиї гравці були найактивнішими.

 

О, переможці!

 В цій тяжкій борні

Ви зберегли азарт геометричний.

Вас зупинить ніякі перепони не змогли,

ви винахідливі у ситуації критичній.

Прийміть вітання, переможці, щирі!

Живімо з геометрією у злагоді і мирі!

Нехай кмітливість вам допомагає,

Геометричні таємниці кожен з вас пізнає!

 

III  Домашнє завдання:

Контрольні питання ст. 42 №33; 34.