Урок геометрії для 8 класу

Тема уроку: Чотирикутники: паралелограм, прямокутник, ромб, квадрат. Тип уроку: урок-КВК  Мета уроку:

 повторити навчальний матеріал з теми;

 розвивати навички використання теоретичного матеріалу для розв’язування задач; використання кількох способів розв’язування задач;

 сприяти розвитку кмітливості, логічного мислення, уваги та уяви, розвитку дослідницької діяльності.

Обладнання: таблиці з готовими малюнками

 

Хід уроку

I. Мотивація навчальної діяльності

Вчитель: Важко уявити собі життя без чотирикутників. Розгляньте предмети побуту, окремих конструкцій будівель, зайдіть до магазину чи в картинну галерею – і ви побачите безліч речей, деталі яких є чотирикутниками. Придивіться до візерунків паркету, що прикрашають музеї або стародавні палаци.

 

Учень: Картина «Чорний квадрат» російського художника К.С.Малевіча        (1878-1935), дитинство та юнацькі роки якого пройшли на Україні, стала початком створеного ним напрямку – супрематизм (від лат. Supremus, що означає «найвищий»)

Супрематизм – різновид абстрактного мистецтва ХХ ст.: комбінування зафарбованих найпростіших геометричних фігур (квадрата, полос, трикутника тощо)

                                Супрематизм      значно      вплинув      на      розвиток      декоративно-

оздоблювального мистецтва та стиль меблів, посуду, одягу, зачісок і навіть на оформлення друкованих видань та виготовлення різнокольорової тари, що має чотирикутні форми.

 

Чорний квадрат

Вчитель: Підтвердженням розповіді є архітектурні споруди 20-30 рр. ХХ ст. у Києві, Москві, Ленінграді, Нью-Йорку, окремі приміщення, палаци, музеї, картинні галереї.

 

II. Знайомство з командами Команди сформувалися заздалегідь.

Команда обирає капітана і назву, виготовляє емблему; готує домашнє завдання («Довести ознаку паралелограма: якщо у паралелограма дві сторони рівні і паралельні». Підготувати найбільшу кількість способів доведення, комбінацію кількох.)

З метою обрання тієї команди, яка розпочинає перша, учням пропонується казка-питання:

Одного разу зібралися всі чотирикутники на лісовій галявині і стали обговорювати питання про вибір свого короля. Довго сперечалися і ніяк не могли прийти до однієї думки. І ось один старий паралелограм сказав: "Давайте підемо всі до царства чотирикутників. Хто першим прийде, той і буде королем." Всі погодилися. І рано вранці вирушили в далеку подорож. На шляху їм зустрілася річка, яка сказала , що перепливуть її тільки ті, у кого діагоналі перетинаються і діляться навпіл. Частина чотирикутників залишилася на березі, а інші переправилися і пішли далі. Але незабаром на шляху їм зустрілася гора, яка сказала, що дозволить пройти тільки тим, у кого діагоналі рівні. Декілька мандрівників залишилася у гори, інші продовжили шлях. Дійшли вони до обриву, де був вузенький місточок. Міст поставив умову, що пропустить тільки тих, у кого діагоналі перетинаються під прямим кутом. У підсумку по мосту пройшов тільки один чотирикутник, який першим дістався до царства і був проголошений королем. Хто став королем чотирикутників?

(Відповідь: переправились через річку: ромб, квадрат, прямокутник, паралелограм. Через гору перейшли: квадрат і прямокутник. Через міст пройшов тільки квадрат. Він і став королем чотирикутників.)

 

III. Розминка

Командам по черзі пропонується розв’язати задачу за готовим малюнком (3 б.)

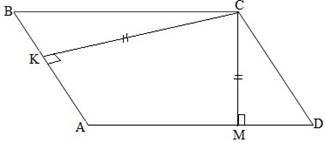Дано: АВСD - паралелограм

CM=CK

Довести: ABCD - ромб

 

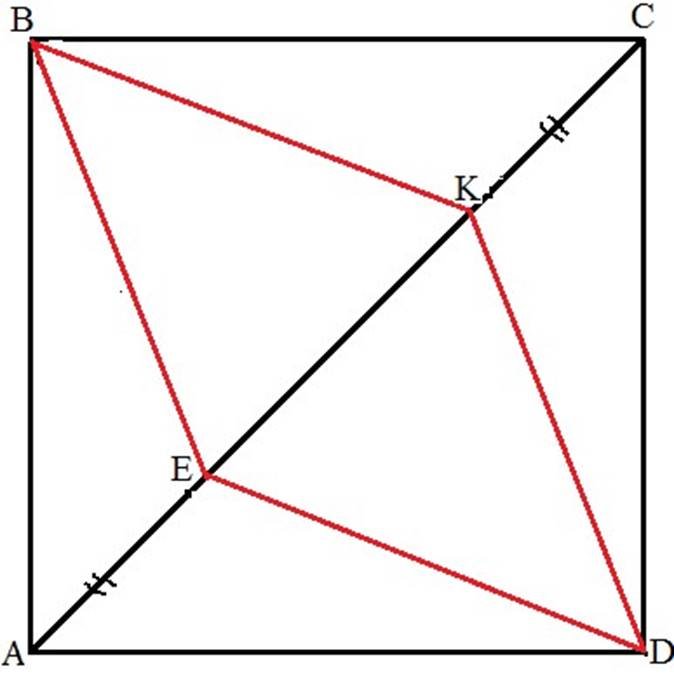
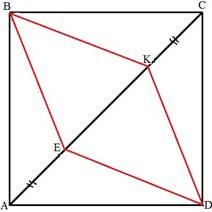Дано: АВСD - квадрат AE=CK

Довести: BEDK - ромб

 

 

 

IV. Конкурс «Щасливий випадок»

Якщо команда не може дати відповідь, то говорить: «далі» (1 б.).  Запитання для першої команди:

1.  Чи можна стверджувати, що чотирикутник, у якого дві сторони паралельні, а дві інші рівні, ромб?     (ні)

2.  Чи можна стверджувати: якщо в чотирикутнику діагоналі не перпендикулярні, то цей чотирикутник не ромб?   (так)

3.  Кожний з трьох кутів чотирикутника дорівнює 100^о. Знайдіть градусну міру його четвертого кута.       (60^о)

4.  Чи правильне твердження: існує ромб, який є прямокутником? (так)

5.  Про паралелограм відомо, що жоден з його кутів не є тупим. Що це за паралелограм?      (прямокутник)

6.  У чотирикутнику точка перетину діагоналей ділить їх на чотири рівні відрізки. Якого виду цей чотирикутник?  (прямокутник або квадрат)

7.  Сума двох кутів паралелограма дорівнює 100^о. Чому дорівнює кожний з цих кутів?        (50^о,50^о)

8.  У якого ромба висота дорівнює стороні?                      (у квадрата)

9.  У прямокутнику діагональ у 2 рази більша за сторону. Який кут між діагоналями цього прямокутника?     (60^о або 120^о)

 

Запитання для другої команди:

1.     Якщо чотирикутник є прямокутником, то його діагоналі рівні між собою.

                Чи правильно обернене твердження?                                            (так)

2.     Чи правильно, що кожний квадрат є прямокутником?           (так)

3.     Чи можна накреслити опуклий чотирикутник, у якого три кути – прямі, а четвертий – гострий?       (ні)

4.     Один з кутів паралелограма дорівнює 70^о. Чому дорівнюють інші його кути?

                                                                                                   (70^о, 110^о, 110^о)

5.     Чи правильно, що ніякий прямокутник не є ромбом?            (так)

6.     За якої умови діагональ ромба дорівнює стороні?     (гострий кут ромба 60^о)

7.     Чи може один кут паралелограма дорівнювати 75^о, 35^о?                  (ні)

8.     Чи правильно, що висоти ромба рівні?                                              (так)

9.     Знайдіть кути ромба, якщо відомо, що його периметр у 8 разів більший за висоту.  (30^о, 150^о, 30^о, 150^о) 

                                         

V. Конкурс художників (2 б. за кожний спосіб)

2 художники від кожної команди отримують завдання: 

«Побудувати ромб за тупим кутом та меншою діагоналлю»

 

I.       Спосіб

План побудови:

1)    Побудувати А, який дорівнює даному.

2)    Провести бісектрису цього кута та відкласти АС.

3)    Через точку С провести СВAD;CDAB.

 

II.    Спосіб

План побудови:

1) Поділити А навпіл. 2) Провести АС.

3)    Відкласти кути, які дорівнюють половині А з вершинами А і С.

4)    Промені перетинаються в точках В і D.

 

III. Спосіб

План побудови:

1)    Побудувати А, який дорівнює даному.

2)    Провести бісектрису цього кута.

3)    Відкласти АС.

4)    Поділити АС навпіл точкою О.

5)    Через точку О провести перпендикуляр до АС.

6)    Точки перетину перпендикуляра зі сторонами кута – В і D.

 

У цей час товариші по команді працюють і отримують таке завдання: (кожне завдання по 1 б.)

1)    Накресліть чотирикутник,     діагоналі    якого          рівні, але    який не      є прямокутником.

2)    Накресліть чотирикутник, у якого діагоналі взаємно перпендикулярні, але який не є ромбом.

3)    Накресліть чотирикутник, діагоналі якого рівні і перпендикулярні, яле який не є квадратом.

 

IV. Конкурс капітанів

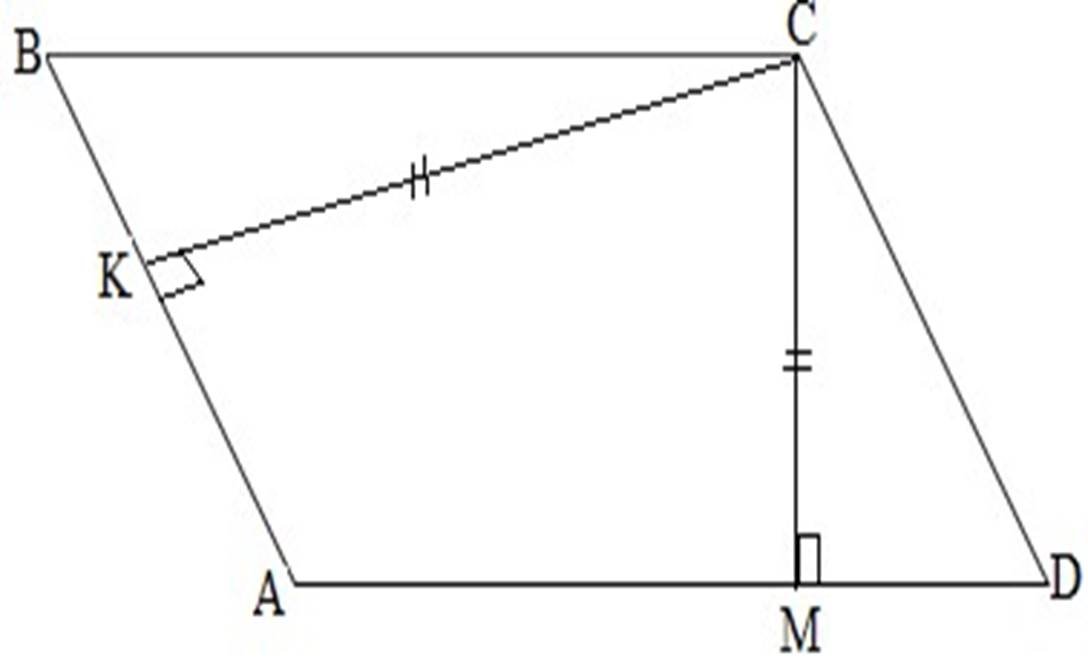
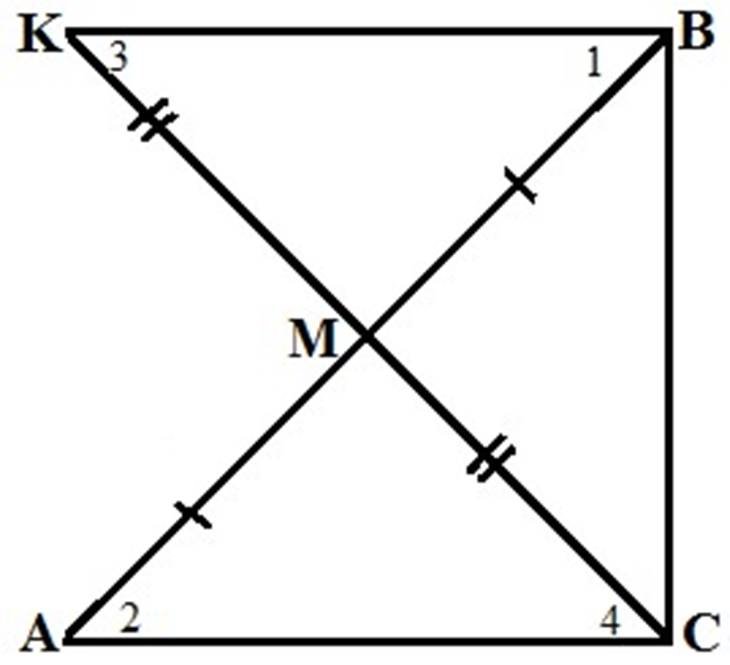
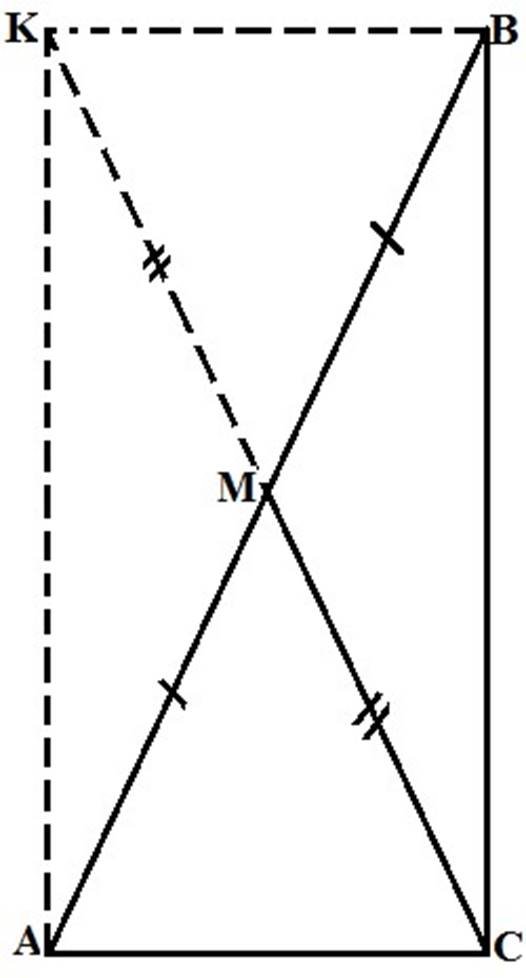
Довести властивість медіани, яка проведена з вершини прямого кута до гіпотенузи     (2 способи – по 3 б. з кожен спосіб)

 

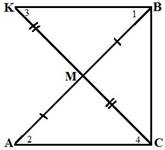І спосіб

Доведення:

1)      Додаткова побудова (д.п.): продовжимо СМ за точку М, так що СМ=МК, з’єднаємо В і К.

2)      АМСВМК (за 2-ма сторонами та кутом між

                                                                            ними)

12;ВКАС;34 але1 та 2 - (внутрішні різносторонні) ВКАС

АСВСВК180⁰ СВК90⁰

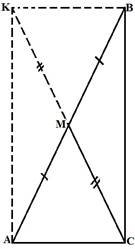ІІ спосіб

Доведення:

1)      Д.п.: побудуємо СК так, що СМ СК , одержуємо чотирикутник АКВС.

2)      Аналогічно (із І сп.) ВС90⁰,ВКАС,ВКАС

АКВС – паралелограм і прямокутник (за ознакою)

СК=АВ (властивість прямокутника) СМ СК 

                                                                            СМ АВ

3)      АВСКВС (за 2-ма катетами)

СКВА;СМСКСМАВ

Поки капітани готуються:

1.     Назвіть спільні (І команда) і відмінні (ІІ команда) властивості прямокутника і ромба

2.     Відомо, що 5²=25 10²=100; половина в квадраті =  , третина в квадраті =; а чому дорівнює кут у квадраті?      (90⁰)

 

Практичні задачі.

 

Завдання для І команди

1.   

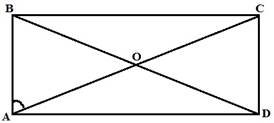
Дано: ABCD – прямокутник,

ВАС 55⁰ Знайти: СОD,ACB

2.   

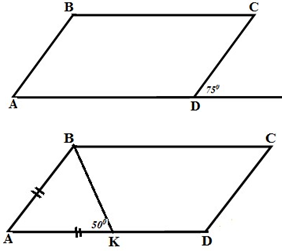
Дано: ABCD – ромб.

Знайти: AВВ

3.   

Дано: ABCD – паралелограм,

         АВАК,АКВ 50⁰ Знайти: кути ABCD

 

 

Завдання для ІІ команди

1.   

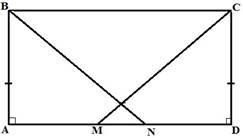
Дано: ABCD – прямокутник,

         BN і CM - бісектриси

 

Довести: BN = CM

2.   

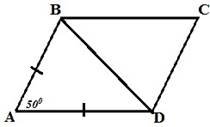
Дано: ABCD – ромб.

Знайти: BDC

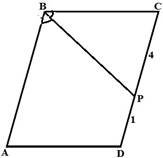3.  Дано: ABCD – паралелограм,

ВЗ – бісектриса, СР=4, DP=1

Знайти: РABCD

1.     Як не вимірюючи кутів чотирикутника земельної ділянки, можна дізнатися, чи вона квадратна?

(мають бути рівними діагоналі та сторони)

2.     Майстер-паркетчик хоче переконатися, що випиляні з дуба чотирикутники – квадрати. Чи достатньо для цього рівності:

           а). Рівності 4-х сторін?                               (ні, може бути ромб)

           б). Рівності діагоналей?                              (ні, може бути прямокутник)

в). Рівності чотирьох відрізків поділу діагоналей?

(ні, може бути прямокутник)

Відповідь: Потрібна одночасна рівність сторін та рівність діагоналей.

 

3.     Кравчиня хотіла перевірити ,чи має клаптик тканини квадратну форму. Вона перегнула його по діагоналі, переконалася, що краї клаптика збігаються, і зробила висновок, що він квадратний. Чи досить цієї

                перевірки?                                                                 (ні, може бути ромб)

 

 

V. Підведення підсумків конкурсу і визначення переможців

 

 

VI. Домашнє завдання

1.     Д/м. Мерзляк: стор. 48 рівень А) 65,66,69; рівень Б) 58,70

2.     Підготувати геометричний диктант

 

Завершити урок хочеться двома висловами:

-         «Лучший способ изучить что-либо – это открыть самому»

-         «Если хотите научиться плавать, то смело выходите в воду, а если хотите научиться решать задачи, то решайте их»

Д.Пойа