Матеріали до уроку "Графік функції y=tgx, її графік та властивості"

Про матеріал

Матеріал до уроку, а саме математичний диктант для перевірки теоретичних знань учнів по темі "Функція y=tgx, її графік та властивості". Якщо учень правильно відповість за запитання, то складе вислів Конфуція. Правильні відповіді виділені червоним кольором.

Перегляд файлу

Математичний диктант

Перед людиною є три шляхи до пізнання:

шлях мислення - найбільш благородний,

шлях наслідування - найбільш легкий

і шлях особистого досвіду – найбільш важкий.

Конфуцій

Тригонометрія ґрунтується на співвідношенні подібності
Відношення довжин сторін у подібних трикутників однакове, тому відношення сторін прямокутних трикутників залежить тільки від одного параметра — гострого кута.
Спочатку тригонометричні функції були пов'язані з співвідношеннями сторін у прямокутному трикутнику. Їхнім єдиним аргументом є кут (один з гострих кутів цього трикутника), тому тангенс - відношення протилежного катета до прилеглого.
Дані визначення дозволяють обчислити значення функцій для гострих кутів, тобто від 0 до 90 (від 0 до 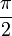$\ Pi \ over 2$ радіан). У XVIII столітті Леонард Ейлер дав сучасні, більш загальні визначення, розширивши область визначення цих функцій на всю числову вісь. Тангенсом кута повороту ɑ називають відношення синуса цього кута до його косинуса.
Пряму паралельну осі ОУ, що проходить через точку з координатами (1;0) називають віссю тангенсів.
Вираз tqx має смисл при будь-якому х, крім чисел виду

х =

Оскільки tqɑ - це ордината точки Т_ɑлінії тангенсів, то областю значень тангенса є R.
Оскільки точки Т_ɑ і Т_-ɑ симетричні відносно Р_о лінії тангенсів, то

tq(-ɑ) = - tqɑ.

При зміні кута від - π/2 до π/2 ордината точки Т_о лінії тангенсів збільшується від -∞ до + ∞, тобто tqɑ зростає на проміжку (-π/2;π/2).
Найменший додатній період тангенса дорівнює π.

Математичний диктант

1	співвідношенні рівності	співвідношенні подібності	співвідношенні неподібності
1	Перед твариною	Перед людиною	Перед учнем
2	прямого кута	гострого кута	тупого кута
2	є один шлях-	є три шляхи -	є безліч шляхів-
3	котангенс	синус	тангенс
3	до науки:	до роботи:	до пізнання:
4	відношення синуса цього кута до його косинуса	відношення косинуса цього кута до його синуса	відношення синуса цього кута до синуса другого кута
4	шлях мислення	шлях вивчення	шлях повторення
5	віссю котангенсів	асимптотою	віссю тангенсів
5	- найбільш дорогий,	- найбільш дешевий,	- найбільш благородний,
6	х =	х =	х =
6	шлях наслідування -	шлях предків -	шлях вчителів -
7	R	Z	N
7	найбільш легкий	найбільш приємний	найбільш точний
8	tq(-*ɑ) = -* tqɑ	tq(-*ɑ) = -* tqɑ	tq(-*ɑ) = -* tqɑ
8	і шлях особистого	і шлях друга	і шлях однокласника
9	спадає	зростає	сталий
9	навчання -	досвіду -	розуму -
10	2π	3π	π
10	найбільш зрозумілий.	найбільш вдалий.	найбільш важкий.