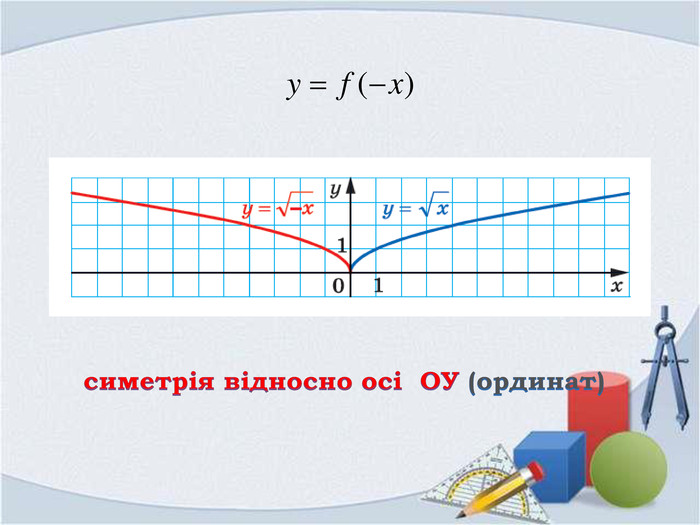
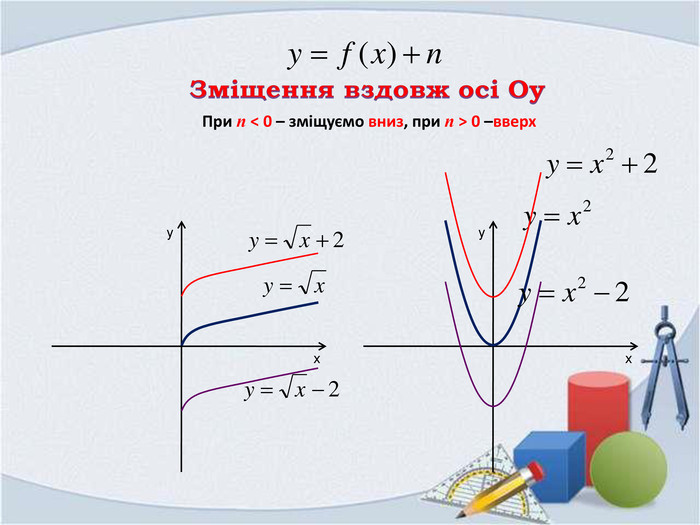
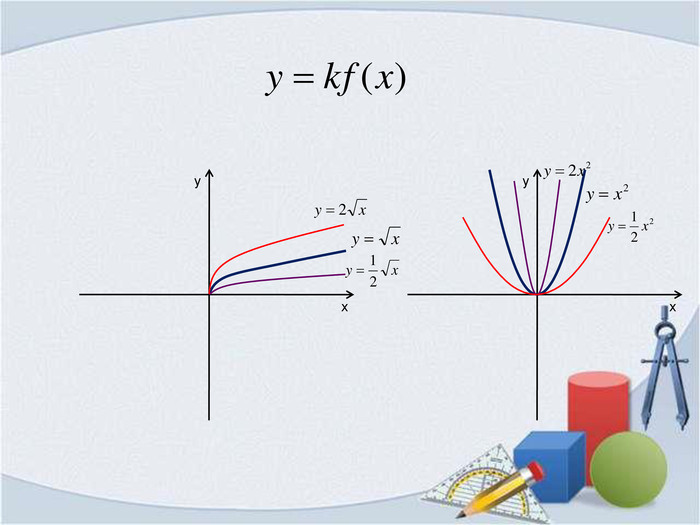
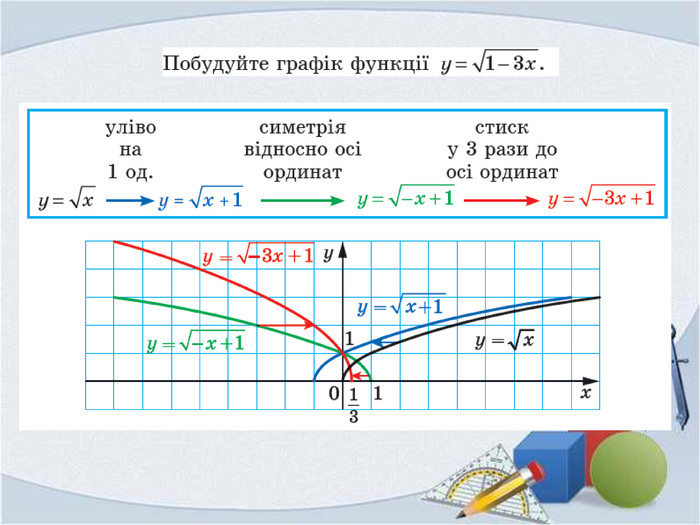
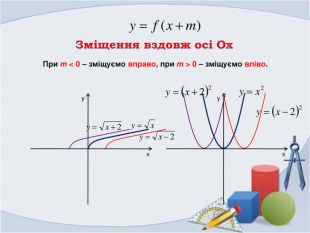
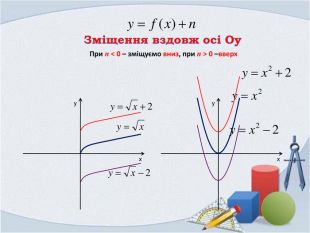
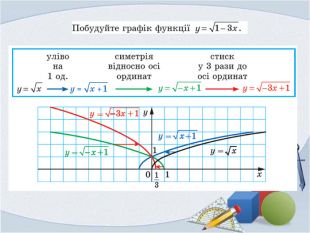
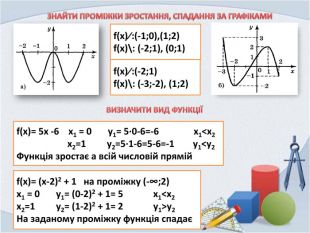
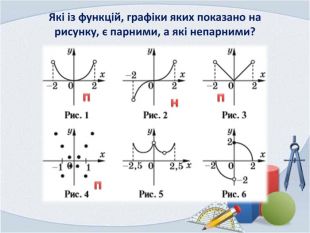
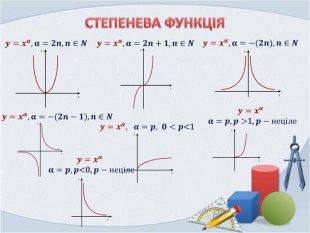
Презентація "Фукнції, їх властивості та графіки"
Про матеріал
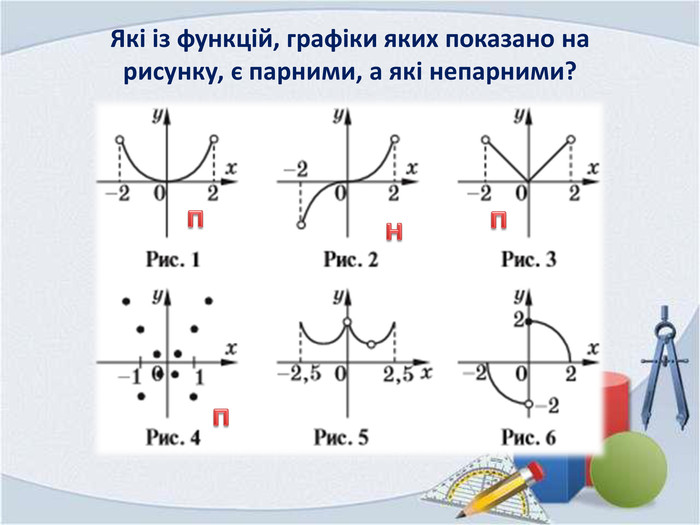
В презентацї містяться матеріали до узагальнення теми "Функції, їх властивості та графіки". Можна використовувати при підготовці до контрольної роботи з даної теми. Крім коротких теоретичних викладок на повторення властивостей функцій, містяться вправи на дослідження функцій та та побудови графіків з використанням їх перетворень. Деякі завдання у форматі завдань ЗНО Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
-
Блискуче! Дякую!
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



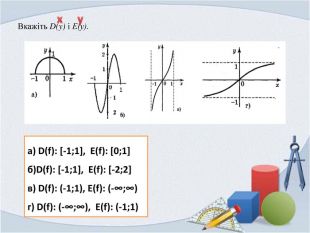
![Вкажіть D(y) і Е(у).хуа) D(f): [-1;1], E(f): [0;1]б)D(f): [-1;1], E(f): [-2;2]в) D(f): (-1;1), E(f): (-∞;∞)г) D(f): (-∞;∞), E(f): (-1;1) Вкажіть D(y) і Е(у).хуа) D(f): [-1;1], E(f): [0;1]б)D(f): [-1;1], E(f): [-2;2]в) D(f): (-1;1), E(f): (-∞;∞)г) D(f): (-∞;∞), E(f): (-1;1)](/uploads/files/182171/206082/222024_images/3.jpg)