Матеріали стенду "Математика в сузір'ї професій"

Математичні моделі в медицині

Математика проникла в усі сфери сучасного життя. Знайшла вона широке застосування і в медицині. Особливо великого значення тут набу­ло математичне моделювання. За допомогою математичних моделей відтворюються навіть органи людини. Що ж являє собою така математич­на модель? У найпростішому випадку  це формули, частіше  системи з десятків і сотень рівнянь, які математично виражають діяльність окре­мих органів людини, перебіг біологічних процесів. Саме на шляху мате­матичного моделювання вчені вбачають процес визволення людства від багатьох хвороб, в тому числі і від серцево-судинних захворювань, рако­вих утворень.

А чи можна, не чекаючи спалахів грипу, передбачити, коли він почнеться? Так. Вчені Київського науково-дослідного інституту епідеміології та мікробіології створили математичну модель епідемії грипу. Це формули з кількома десятками інтегралів, які відображають весь процес передачі захворювання від хворої до здорової людини. За допомогою таких формул можна визначити, коли хвора людина стане найбільш небезпечною для оточуючих, коли і які ліки потрібно давати хворим тощо. Використовуючи теорію ймовірностей і методи математичної статистики, медики разом з математиками можуть вира­хувати, яка кількість мешканців певного регіону буде охоплена черго­вим спалахом грипу чи іншого інфекційного захворювання. Такий діагноз допоможе медикам заздалегідь підготувати відповідні ліку вальні та профілактичні засоби.

Застосування в медицині комп’ютерної техніки

Все більшого застосування в медицині знаходить комп’ютерна техніка. Створено електронні діагностичні комплекси, обладнані десят­ками датчиків та ЕОМ. Вони виконують функції стеження за діяльністю внутрішніх органів хворого.

Під час проведення операцій на серці електронні діагностичні ком­плекси можуть через кожні п’ять секунд висвічувати на табло дані ар­теріального тиску, пульс, температуру, електрокардіограму тощо. Одночасно на іншому екрані ці дані фіксуються у вигляді графіків, тобто кривих ліній. За допомогою встановлених машиною параметрів лікарі контролюють стан хворого.

Електронні медичні прилади дають можливість анестезіологам візуально оцінювати роботу шлуночка, скорочувальну здатність міокарда, різні параметри життєдіяльності організму, які абсолютно недоступні в реальному часі для мозку людини.

З появою сучасних комп’ютерів в медицині дійсно відбувається переворот. Не тільки в лабораторії, а й біля ліжка хворого можна одночасно побачити лікаря, математика і програміста. Прикладом співпраці спеціалістів різного профілю може бути робота колективу Інституту серцево-судинних захворювань, яка називається «Новий підхід в діагно­стуванні й лікуванні розладів кровообігу і застосування математичних мо­делей і методів для впровадження його в практику». У цьому Інституті створена лабораторія математичного моделювання, яка розробила новий напрямок науки  фізіологічну кібернетику.

З’явилися нові поняття, такі, як насосний коефіцієнт наповнення правового і лівого шлуночка серця, опір судинам малого круга, характеристики еластичності судин.

Головне  це не новизна сама по собі, а те, що лікар має можливість створювати індивідуальні математичні моделі для кожного пацієнта і за їх допомогою знаходити й лікувати патологічні зсуви.

Здоров’я й гармонія

Останнім часом починає впроваджуватися симетрійний підхід до оцінки функціонального стану людини. Відомо, що у здорової людини всі фізіологічні показники близькі до норми. Більше того, вони, вияв­ляється, перебувають у певному співвідношенні між собою, адже в ор­ганізмі все взаємопов’язане.

Скажімо, підвищення температури може змінити роботу серця, легень тощо. Регулює це співвідношення вегета­тивна нервова система, підтримуючи баланс, симетрію в роботі своїх відділів: симпатичного й парасимпатичного. І, як виявилось, таке співвідношення може служити діагностичною ознакою здоров’я. В Інституті нормальної фізіології ім. Анохіна були піддані обстеженню кілька сотень здорових і хворих людей. У кожного вимірювали артеріальний тиск, температуру, стан легень, судин  всього більше 20 параметрів. Ці показники автоматично оброблялися на ЕОМ і відкладалися на радіусах одного кута.

Коли сполучили ці показники однією лінією, вийшла крива  гео­метричне зображення стану здоров’я людини. Виявилось, чим кращий стан здоров’я, тим більше наближується крива до кола, а значення фізіологічних параметрів не виходить за межі круга.

І навпаки. Коли радіуси не вміщуються в круг, час починати лікування.

Подальше дослідження показало, що співвідношення математичних значень параметрів у тій моделі, яка може служити еталоном здоров’я, близьке до «золотого перерізу», тієї божественної пропорції, яку вважають мірилом краси й гармонії в усіх видах мистецтв.

Виявляється, і фізіологічні процеси підлягають законам краси та гар­монії.

Математика допомагає селекціонерам

Однією з найважливіших проблем сільського господарства є питання виведення нових сортів сільськогосподарських культур. Цим займається селекція.

Відомо, що при виведенні нових сортів рослин постає багато принци­пово важливих питань: як на основі дослідних даних виявити, чи володіє новий сорт необхідними якостями; чи буде він кращий від попереднього; чи можна вважати, що новий сорт продуктивнішій і стійкіший до захво­рювань? Скільки ж дослідів треба провести, щоб з достатньою перекон­ливістю дати відповіді на поставлені питання! Без методів точної матема­тики тут не обійтися.

У наш час не можна сказати: «Я переконаний, що цей сорт кращий», або «Я сподіваюсь, що до цих ґрунтів він буде пристосованішим». Щоб відповісти на запитання, як планувати й виконувати спостереження, яка кількість дослідів достатня тощо, необхідно звернутися до математичної статистики.

Подивимося, як здійснюється співробітництво біологів-селекціонерів і математиків. Нехай треба вивести новий сорт пшениці. Завдан­ня полягає в тому, щоб шляхом схрещення одержати нові сорти пшениці, які найбільше придатні до певного регіону. Для схрещення підбирають кілька сортів (так, для створення сибірської ярової пшениці було взято 15 сортів). З цих сортів одержують гібридні комбінації, які вирощують потім в кількох географічних районах. На кожній рослині фіксується не менше 15 ознак продуктивності сорту: число і довжина стебел, кількість зерен, кількість білка, протистояння хворобам, морозам та ін.

Така робота може тривати кілька років. В результаті накопичується вели­чезна кількість матеріалу  кілька мільйонів значень різних параметрів,  який неможливо переробити й цілій армії обчислювачів. На допомогу приходить комп’ютерна техніка з потужними ЕОМ. Створюються спеціальні програми для аналізу певних ознак рослин. При цьому засто­совується математичний апарат — кореляційний і факторний аналізи. Після того, як весь експериментальний матеріал оброблено на ЕОМ, створюється банк даних, на основі якого складається атлас домінантних ознак продукції.

Колись основним знаряддям селекціонера була інтуїція та досвід. Те­пер же на основі проведеного аналізу, знаючи генетику ознак продуктив­ності та зв’язки між цими ознаками, можна за допомогою ЕОМ цілеспря­мовано вести схрещування і заздалегідь вибирати такі гібриди, які дадуть заплановане потомство.

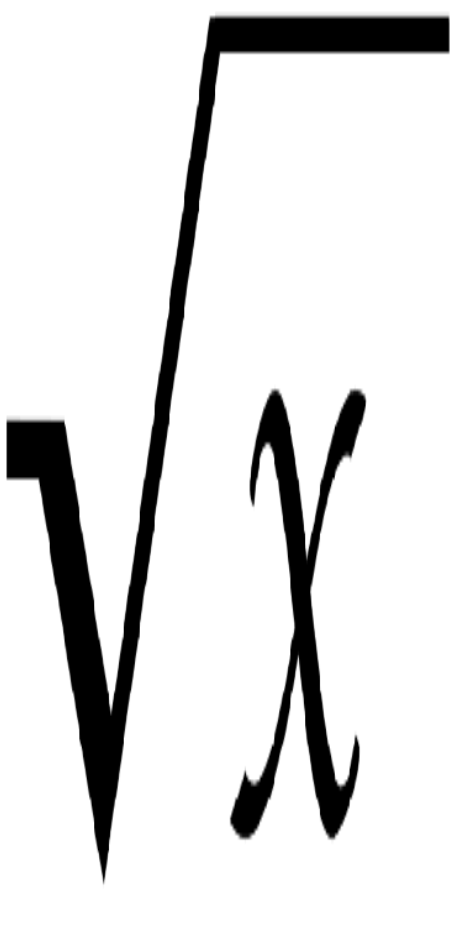
Надійний помічник у роботі геологів

Якщо хтось думає, що шукати під землею родовища можна старим способом: копай, шукай і знайдеш  або ставити бурові вишки рівними рядами  десь та бризне нафтовий фонтан, то він помиляється. На допо­могу сучасним геологам прийшла математика, яка використовує у своїх дослідженнях обчислювальну техніку.

Спочатку землю простукують і прослуховують геофізики. Вони знімають «кардіограму»  акустичну активність різних ділянок Землі, роблять графіки сил тяжіння. На досліджуваній площі геологи утворюють вибух. Він відбивається від усіх ділянок і повертається на поверхню. Тоді за допомогою ЕОМ математики складають сейсмограми.

У процесі пошукової роботи у геологів збирається багато різно­манітних даних, зведень. їх потрібно систематично обробляти. При таких розрахунках використовують методи статистичного аналізу, теорію ймовірностей та інші галузі математичної науки. Здійснивши розрахунки за допомогою ЕОМ, математики можуть підказати геологам, де знахо­диться резервуар з нафтою чи пласт вугілля.

Наскільки точні такі результати? Можна з впевненістю сказати, що математичні прогнози блискуче підтверджуються на практиці. Так, у співпраці з математиками було відкрито ряд нафтових покладів на території Омської області в Сибіру. Три з них  Західно-Осетинське, Лінійне та Льодове родовища   були відкриті, саме там, де пере­дбачили й підказали математики.

Останнім часом у гірничій промисловості знаходять широке застосуван­ня інформаційно-пошукові системи управління вторинними ресурсами.

Такі системи збирають і надають інформацію про можливі способи пере­робки певного відходу, відстань його транспортування, вартість робіт, які необхідно провести, відомості стосовно того, які є обмеження з природо­охоронних питань.

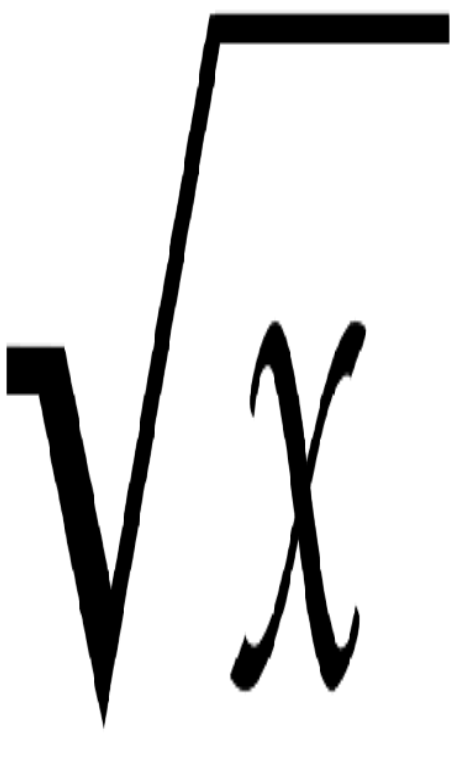
Професія  полярний математик

Кілька років тому з’явилося повідомлення, що зареєстровано виник­нення нової професії  полярний математик. Арктика здавна притягува­ла математиків. Згадаємо Отто Юлійовича Шмідта, який більшу частину свого життя присвятив вивченню й освоєнню Арктики. А видатний дослідник Кропоткін за допомогою математичних теорій і обчислень вив­чив рух криги і течії Північного Льодовитого океану і передбачив існуван­ня невідомої Землі. Пізніше у вказаному ним місці був відкритий архіпе­лаг Шпіцберген.

З 1987 року математики в Арктиці працюють постійно. Праця поляр­ного математика важлива й необхідна для розв’язання багатьох арктич­них проблем. Так, полярні математики збирають й обробляють інфор­мацію про циркуляцію криги в полярному басейні, напрями поверхневих течій, механіку глибинних течій, температуру води, її хімічний склад, хмарність атмосфери, розсіяність радіації та ін.

На станції «Північний полюс» влаштовано обчислювальний центр. Він діє цілодобово. За допомогою електронної техніки математики забез­печують не тільки наукову, а й економічну ефективність роботи поляр­ників. Оброблену за допомогою складених математиками програм інфор­мацію полярники одержують не в закодованому, а в розшифрованому, зрозумілому широкому колу спеціалістів вигляді.

Тепер впевнено можна сказати, що математика  також романтична професія.

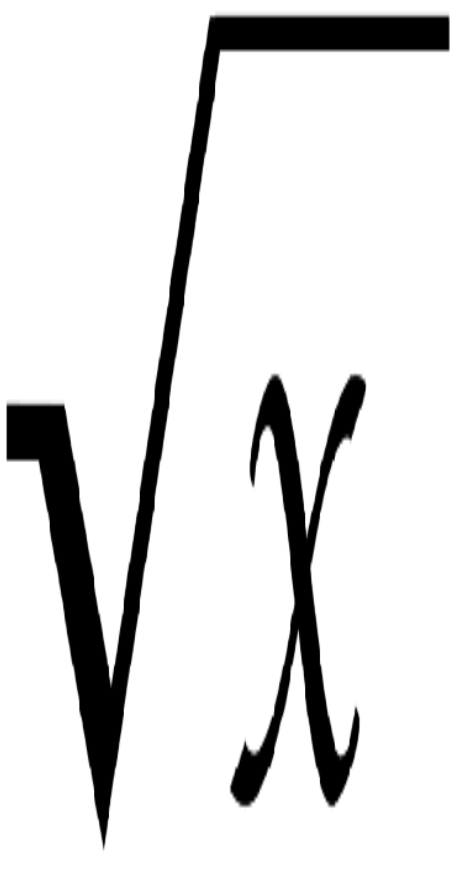
Математика і лісництво

Лісове господарство  складний підрозділ економіки. Організації лісового господарства передує проведення кропіткої роботи. Необхідно здійснити всебічний облік дерев за віком, породами, запасами дереви­ни, умовами проростання, реакцією на хвороби та іншими ознаками.

Технічні дії, спрямовані на всебічний облік лісу, оцінку процесів лісовирощування, виявлення сировинних ресурсів, визначення об’ємів дерев і заготовлення продукції, називається таксацією лісу Це одна з основних лісових дисциплін. Вона має справу з вимірюван­нями, обчисленнями, які дають об’єктивну оцінку різних параметрів лісу. Таксаційні дослідження спираються на методи аналітичної геометрії, теорію ймовірностей, математичну статистику.

Залежність між об’ємом гілки дерева та її діаметром виражається рівнянням параболи четвертого степеня, і вона єдина для кожного дерева. При конструюванні дерева природа скористалася аналогом теореми Піфагора: квадрат радіуса основного стовбура дорівнює сумі квадратів радіусів складових стовбурів, виміряних вище від розгалуження. Об’єм усієї наземної частини дерева залежить від єдиного параметра  діаметра стовбура.

Математичні методи допомагають передбачити приріст та динаміку росту насаджень.

Про таємниці розвитку багатьох порід дерев у різних ґрунтово-кліматичних зонах розповіло їхнє коріння, старанно досліджене з урахуванням найрізноманітніших факторів. Десятки тисяч даних доводиться аналізу­вати на ЕОМ. На основі досліджень учені розробили рекомендації щодо раціонального розміщення насаджень, догляду за ними. За 200-річний період розвитку таксаційної техніки сконструйовано цілий ряд висо­томірів, дія яких пов’язана з геометричними, тригонометричними залеж­ностями та побудовами.

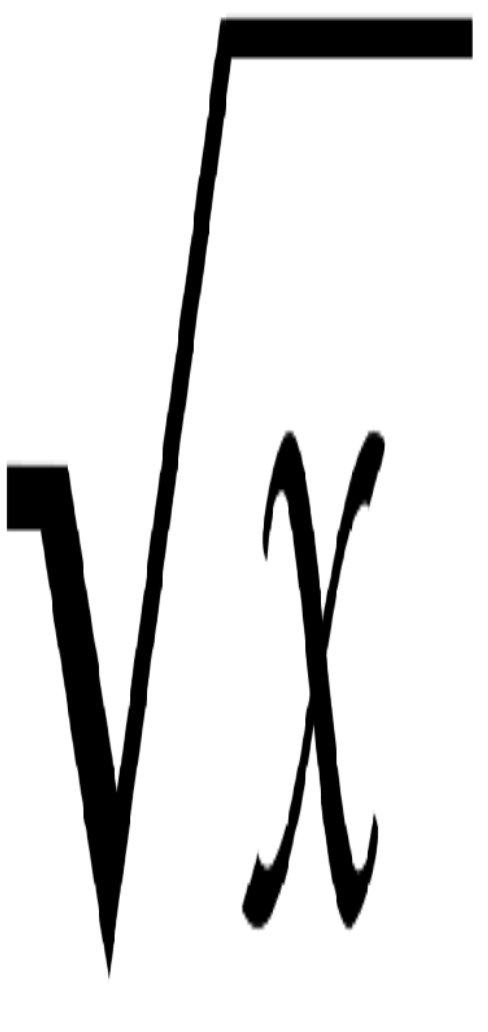Омар Хайям  учений-енциклопедист

Омар Хайям  великий філософ, учений-енциклопедист серед­ньовічного Сходу. Народився в 1048 році (за іншими даними  в 1040) в Нішапурі, одному з найстародавніших іранських міст.

Вважають, що походив він з ремісницької родини, оскільки прізвище Хайям по-аюрськи означає ремісник  майстер наметів.

Старовинні автори розповідають, що Омар Хайям замолоду забагато доклав зусиль, щоб здобути освіту, і в сімнадцять років мав глибокі знан­ня з багатьох наук. «Він був мудрою людиною, обізнаною в усіх галузях філософії, а надто математики!»  писав про нього географ XIII ст. аль-Казвіні.

Все своє життя Омар Хайям присвятив науці. Крім природ­ничо-математичних наук, він вивчає медицину, географію, астрономію, літературу. У тяжкі часи довелося жити й працювати вченому. Війни, пере­вороти, свавілля деспотів-феодалів  всі ці випробування довелося витримувати й Омарові Хайяму. «Я був позбавле­ний можливості систематично займатися науковою діяльністю через мінливість долі,  говорив учений.  Ми були свідка­ми загибелі талановитих творців науки, від яких залишилася нечисленна, але багатост­раждальна купка».

Одним з найвидатніших наукових досліджень Омара Хайяма є праця «Про до­ ведення задач і алмукабали». Ця книга містила майже всю сукупність знань з алгебри того часу. У ній подається класифікація рівнянь і викладається теорія розв’язання              Омар Хайям рівнянь першого, другого і третього степенів. У цій роботі автор визначає алгебру, як науку про знаходження невідомих величин, що перебувають у деякому відношенні з іншими невідомими величинами.

Визначення невідомих здійснюється за допомогою складання і розв’язання рівнянь. Алгебра Хайяма  виключно словесна. Невідоме в його концепції може бути або числом (лише цілим додатним), або гео­метричною величиною: відрізком, площею, об’ємом. Хайям пише, що алгебраїсти звичайно називали невідоме «річчю», її добуток на себе  «квадратом», добуток квадрата на неї  «кубом», квадрата на себе  «квадратом-квадратом» і т. д.

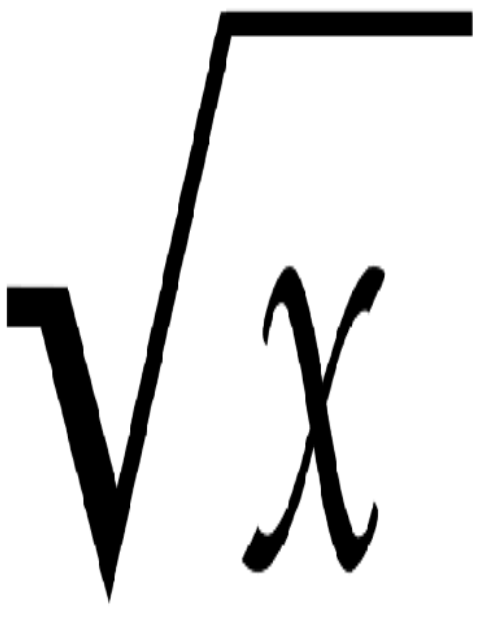Хайям розв’язує деякі види рівнянь, що містять величини, обернені до невідомих, а також їх степені. Ось одна із задач, яка приводить до таких рівнянь: доля квадрата дорівнює половині долі кореня.

При розв’язанні одержується таке рівняння:

 .

Слави як алгебраїст Хайям здобув завдяки теорії геометричного розв’язання рівнянь третього степеня. Пе­ред ученими того часу стояло завдання  класифікувати кубічні рівнян­ня, побудувати теорію геометричного їх розв’язання і створити систему дослідження коренів. Ця задача була розв’язана Хайямом.

У 1077 році вчений закінчив роботу над важливою математичною пра­цею «Коментарі до важких постулатів Евкліда». Цей трактат складається з трьох частин, які містять теорію паралельних прямих, теорію відношень і пропорцій.

Ще одна праця Омара Хайяма «Про мистецтво визначення кількості золота й срібла» мала на той час великий успіх. Вона присвячена кла­сичній проблемі розв'язання задач на змішування. Хайям написав кілька трактатів з географії, астрономії, філософії.

Помер учений у 1123 році. У і 934 році в Нішапурі на його могилі був споруджений монументальний обеліск-пам’ятник.