Майстер-клас «Дослідницька діяльність на уроках математики, як метод SТЕМ-освіти»

Майстер-клас

«Дослідницька діяльність на уроках математики, як метод SТЕМ-освіти»

Добрий день. Вітаю всіх на моєму майстер-класі на тему «Дослідницька діяльність на уроках математики, як метод SТЕМ-освіти»

В сучасному світі активно розвиваються такі галузі, як будівництво, транспорт, промисловість. Інженерні та технічні професії актуальні, особливо, якщо спеціалістами є нове покоління. Це люди, кваліфіковані не в одній галузі, а декількох. І можуть швидко, комплексно, креативно вирішити поставлені перед ними завдання. Тому добре коли освіта передбачатиме яким має бути розвиток суспільства і готуватиме молодь конкурентоспроможну на ринку праці.

Хорошим помічником на уроках може стати STEM-освіта, як дієвий метод навчання математики. Це популярний напрям в світі, що охоплює природничі науки, технології, технічну творчість (інжиніринг) та математику.

Наука передбачає вивчення навколишнього світу, законів природи, що пов’язані з фізикою, хімією, біологією. Технологія включає в себе  систему організацій, людей, знань, пристроїв, які входять до технологічної діяльності. Інжиніринг дає змогу знайти способи вирішення проблеми. Математика вивчає зв’язки, закономірності величин, цифри і форми.

STEM-освіта передбачає застосування методу проектів, ігрових методик, практичних, лабораторних робіт, дослідницької діяльності. Все це допомагає розвивати такі якості дитини як: творче технічне мислення, кмітливість, винахідливість, інтуїція, вміння знаходити вірне рішення в складних та суперечливих ситуаціях.

Зосередимось на навчально-дослідницькій діяльності учнів на уроках математики. Це вид навчально-пізнавальної роботи, яка спрямована на пошук, вивчення й пояснення математичних фактів для здобуття й систематизації суб’єктивно нових знань і способів їх використання на практиці. Її мета розвивати цікавість до навколишнього світу, до математичної науки, розвиток мислення учня і можливість побувати в ролі вченого математика, який вивчає новий об’єкт чи процес. Дослідницький метод пізнання природній, він має стадію підготовки, де проявляється активність, цікавість, очікування дослідження, а в процесі його виконання, учні відчувають себе учасниками, творцями дослідження, проявляється захоплення, кмітливість і задоволення.

Навчально-дослідницька діяльність має особливості і в-першу чергу вона пов’язана з розв’язуванням учнями творчих завдань. На основі тих знань і умінь, які вони вже мають діти розвивають логіку, уяву, критичне мислення, вчаться актуалізувати, робити висновки, презентувати результат зробленої роботи. Наступна особливість полягає в тому, що науково-дослідницька діяльність учня обов’язково має проходити під керівництвом вчителя. Адже під час виконання дослідження учень може допустити помилку і отримає невірний результат. Тому важливо вчасно виправити помилку і не дати закріпитись в свідомості учня хибного уявлення про досліджуваний об’єкт. Запам’ятатись повинен правильний висновок. Однією з особливостей навчально-дослідницької діяльності є продукування нових знань, які будуть посильними учням. І завдання треба будувати так, щоб їх могли виконувати всі учні, не залежно від рівня їх математичної підготовки, крім того, необхідно використовувати технічні і наочні засоби, щоб діти легше сприймали  матеріал. І ще одна, дуже важлива особливість науково-дослідницької діяльності – індивідуалізація, тобто кожен учень повинен виконувати ті чи інші завдання і набувати знання, вміння та навички.

Ознайомимось з основними етапами математичного дослідження. Спочатку учні стикаються з проблемою і щоб її розв’язати знань, які вони мають, недостатньо. Тому саме час дізнатись нові факти з теорії, стосовно даної проблеми. Далі відбувається підбір методів дослідження, а потім учні збирають матеріал, аналізують його і узагальнюють. Наступний етап складний, але дуже важливий, необхідно все обдумати обов’язково додати науковий коментар і кожен учень повинен зробити власний висновок щойно виконаного дослідження. Послідовне виконання етапів дослідження є важливим у виконанні дослідницької роботи і вчителю варто про це наголошувати, щоб процес відбувався ефективно.

Приклади дослідницьких прав

Завдання 1

В 5 класі, під час вивчення теми «Об’єм прямокутного паралелепіпеда, дітям можна роздати малюнки прямокутного паралелепіпеда.

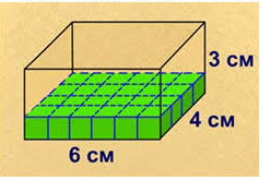
І поставити запитання: «Як знайти об’єм прямокутного паралелепіпеда з вимірами 6 см, 4 см і 3 см?

Діти звертають увагу на те, що всередині фігури уже є якась кількість одиничних кубиків і озвучують гіпотезу: Потрібно порахувати всі кубики, які заповнять паралелепіпед повністю.

Діти рахують одиничні кубики, аналізують поетапність своїх підрахунків. Потім записують дані в таблицю

Вчитель пропонує узагальнити свій результат і написати вираз, обчисливши який можна знайти таку ж кількість одиничних кубиків. А далі завдання: «Напишіть формулу для знаходження об’єму прямокутного паралелепіпеда з вимірами a, b, c.»

Діти роблять висновки свого дослідження. Формулюють правило знаходження об’єму прямокутного паралелепіпеда.

Далі можна обговорити питання одиниць вимірювання об’ємів.

І запропонувати дітям наступні завдання.

1. Виміряй довжину, ширину, висоту свого прямокутного паралелепіпеда. Усі виміри занеси у таблицю. Знайди об’єм прямокутного паралелепіпеда.

2. Уяви, що довжина твого паралелепіпеда вдвічі менша. Досліди, як зміниться об’єм твого прямокутного паралелепіпеда. Запиши нові дані в таблицю. Знайди об’єм прямокутного паралелепіпеда. Порівняй його з об’ємом початкового паралелепіпеда.

3. Досліди, як зміниться об’єм початкового прямокутного паралелепіпеда, якщо збільшити його ширину в 3 рази. Запиши нові дані в таблицю. Знайди об’єм прямокутного паралелепіпеда. Порівняй його з об’ємом початкового паралелепіпеда.

4. Запиши висновок своїх досліджень.

Завдання 2

Під час вивчення способу множення десяткових дробів на розрядні одиниці можна використати розрядну таблицю, як при введенні способу множення натурального багатоцифрового числа на 10, 100, 1000 і т.д.

1. Розмістіть число 2,345 в розрядній таблиці:

Діти записують:

І далі постановка проблеми. «Спробуйте виконати множення десяткового дробу на 10, 100, 1000. Скористайтесь розрядною таблицею.»

2. Діти пригадують, що помножити будь-яке число на розрядну одиницю – це все одно, що помножити його на одиницю відповідного розряду і це означає, що для того, щоб знайти значення добутку позиційного числа та розрядної одиниці, треба число просто «перемістити» в розрядній таблиці. Наприклад, якщо множимо число на 10, то це число «переміститься» в розрядній таблиці на один розряд ліворуч.
3. Діти висловлюють думки, що множення десяткового дробу на розрядні одиниці відбувається так само, як множення натурального числа на розрядні одиниці. І виконують запропоновані вправи.

4. Виконуючи таким чином всі завдання треба звернути увагу учнів на «рух коми», зробити висновки і в результаті сформулювати правило знаходження значення добутку десяткового дробу та розрядної одиниці (10, 100, 1000… та 0,1; 0,01; 0,001…)
5. Після виконання такої дослідницької роботи вчитель пропонує дітям зробити власні висновки. Наприклад відповісти на такі запитання: «Що я сьогодні навчився?», «Що з того, що я вже вмів, знадобилось під час виконання завдань?», «Чи сподобалось мені самостійно сформувати алгоритм множення десяткових дробів на розрядну одиницю?», «Що було зробити тяжко а що вдавалося легко?»

Завдання 3

Розглянемо задачу, на прикладі якої можна показати, що математика має вагомий потенціал для розуміння учнями цінності життя і здоров’я. Підсилити важливість наскрізної лінії «Здоров’я і безпека» можна словами  Кеннета Купера. Це доктор медицини, колишній полковник ВПС з Оклахоми, який ввів поняття аеробіки. Він автор книги «Аеробіка» (1968), який підкреслив бальну систему для поліпшення серцево-судинної системи. Основою  підтримки хорошого фізичного стану є проходження пішки 10000 кроків на день.

Кеннет Купер казав: «Наш організм створений на 120 років життя. Якщо ми живемо менше, то це викликано не недоліками організму, а тим, як ми з ним поводимося».

Задача: «У каві та чаї міститься кофеїн. Вміст кофеїну в чашці кожного з напоїв подано на діаграмі.

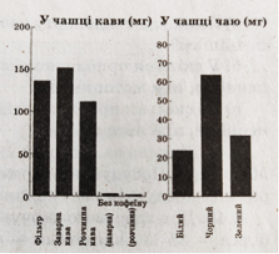1. Скільки кофеїну міститься в чашці:

• Заварної кави;
• Фільтрованої кави;
• Чорного чаю;
• Зеленого чаю;

2. Максимальна безпечна доза кофеїну для дорослої  людини – 400мг.  Яку найбільшу кількість чашок заварної кави можна випити протягом дня».

Діти вчаться працювати з даними поданими в діаграмі, виписують необхідний матеріал, аналізують його і узагальнюють. А також дізнаються цікаві факти, корисні для збереження власного здоров’я. А саме, що вживати каву дітям можна лише з 14-15 років. Вміст кофеїну призводить до перезбудшення і порушення роботи серця. Крім того, кофеїн вимиває кальцій з організму, тоді як цей мікроелемент просто необхідний для систем і органів дитини. Краще каву замінити цикорієм, ячменем або шипшиною. Вони смачні і дуже корисні.

Завдання 4

Пропоную розв’язати задачу з теми «Функція» (7клас) про популяцію зубрів.

«Створюючи заповідник зоологи не можуть помістити туди будь-яку кількість тварин одного виду. Для комфортного співіснування їх число встановлюють за допомогою спеціальних розрахунків. Наприклад, для визначення чисельності зубрів враховують, що на початок потрібно 50 особин, а кожного наступного року t кількість зростатиме на  3 особини.

Чи є вказане правило функцією? Якщо є, то задайте його формулою. Скільки років має пройти з моменту заселення зубрів до заповіднику, щоб їхня кількість зросла до 56 особин;  до 80 особин;  до 167 особин?

Учні не тільки формують уміння та навички подання функції у вигляді формули, вони ще формують навички знаходження значення аргументу за значенням функції, а також дізнаються цікаву інформацію про створення заповідників, а саме, що визначення кількості тварин підпорядковується певним правилам, і це залежить від терміну перебування виду на його території.

Завдання 5

Гарною основою для вивчення геометрії може стати орігамі. Шляхом складання фігур можна будувати інші фігури і можна вивчати властивості геометричних фігур та їх елементів.

1. Виберіть серед запропонованих фігур трикутник і складіть його так, щоб лінією згину один з кутів трикутника був поділений навпіл. Так формується поняття бісектриси кута.
2. Виберіть серед запропонованих фігур прямокутник. Чи можна з прямокутника зробити квадрат? За допомогою складання зробіть квадрат і ножицями відріжте зайву частину. Як називається лінія згину, яку ви отримали в квадраті? Чи можна побудувати ще одну діагональ? Яке взаємне розміщення цих відрізків? На які фігури поділено квадрат? Скільки таких фігур? Назвіть вид трикутників? Доведіть їх рівність. Назвіть властивість діагоналей квадрата.
3. Виберіть серед запропонованих фігур квадрат. Скільки кутів у квадрата? Яка градусна міра кута? Як кут поділити на три рівні частини? … Виникає проблемна ситуація. Скільки градусів буде градусна міра однієї з трьох таких частин; а двох разом? В якому трикутнику кути рівні і мають градусну міру 60 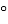? Які ви ще знаєте властивості рівностороннього трикутника? Використаємо сторону квадрата, як сторону трикутника і знайдемо її середину. Для цього зігнемо квадрат навпіл. Ця лінія проходить через середину сторони і розміщена під яким кутом до сторони квадрата? Як називається така лінія? Так, це серединний перпендикуляр до сторони і на ньому знаходиться третя вершина рівностороннього трикутника. Як її знайти? Нижній правий кут прикладіть до лінії перегину. Новий згин перетинає серединний перпендикуляр в точці, що є вершиною трикутника і відрізок між цією точкою перетину і вершиною квадрата є стороною трикутника, отже кут вже поділено на дві частини, одна з них 30 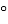а друга 60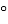. Лишилось більшу частину поділити згином на дві рівні частини.
4. Виберіть серед запропонованих фігур ще один квадрат. Перегніть по діагоналі. Яка фігура утворилася? Скільки вона має кутів? Доведемо теорему про суму кутів трикутника. Знайдіть серединки кожної сторони трикутника. Згинайте трикутник по відрізку, кінцями якого є дві такі середини сторін. Як називається цей відрізок? Так, середня лінія трикутника. Два інші кути трикутника згинаємо так, щоб кути трикутника не накладались один на одного. Разом три кути утворили розгорнутий кут.
5. Аналогічно можна довести суму гострих кутів прямокутного трикутника. І відповівши на ряд запитань встановити, що сума кутів квадрата дорівнює 360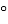. А чи тільки квадрат складається з двох трикутників? Який висновок ми можемо зробити про суму кутів чотирикутника?
6. Візьміть прямокутний лист паперу і перегніть його по діагоналі. Чи будуть рівні трикутники? Чому? Що можна сказати про площі цих трикутників? Як можна обчислити площу кожного? Які виміри потрібно провести, щоб знайти площі трикутників і прямокутника.
7. Виберіть серед запропонованих фігур трикутник. Утворіть в ньому висоту, тобто перпендикуляр, проведений з вершини трикутника. Виміряйте довжину перпендикуляра і сторону трикутника, до якої перпендикуляр проведено. Помножте ці величини. Побудуйте в зошиті прямокутник одна сторона якого дорівнює виміряній в трикутнику висоті, а друга сторона якого дорівнює виміряній стороні трикутника. Знайдіть площу цього прямокутника. Порівняйте отримані добутки. Накладіть на прямокутник трикутник, так, щоб рівні сторони сумістились. Опишіть свої спостереження і поясніть якою буде площа трикутника.
8. Виберіть серед запропонованих фігур два трикутники. Один з них поділіть на два рівновеликі трикутники. А другий – на чотири рівновеликі трикутники.
9. Виберіть серед запропонованих фігур два квадрати. З одного утворіть ромб. З другого утворіть рівносторонній трикутник.
10.  І для задоволення, чи для відпочинку Пропоную виготовити своїми руками орігамі-кубик з шести модулів. Для цього вам потрібно шість однакових квадратів ( я їх підготувала по два різного кольору). Керуючись підказками відео виготовляємо кубики.

Висновок

STEM-задачі об’єднують в собі знання декількох галузей, стимулює до активної пошукової, дослідницької, творчої роботи, ще й показує прикладну направленість математики. Сучасна школа орієнтується на здобуття учнями певних компетентностей, які є необхідними в життєдіяльності кожної людини. За допомогою STEM-освіти реалізовуються такі підходи: діяльнісний, особистісно орієнтований, розвивальний, аксіологічний. Запровадження STEM-освіти потребує змін в поєднанні змісту і методів освіти, створення сучасних технологій навчання математики. Це потребує часу і звичайно бажання. Тому бажаю всім нам творчості, креативності і можливість втілювати обрані вами методи в своїй діяльності.

Використані джерела

1. Я дослідник. Математика. 5 клас : Робочий зошит учня / Д. В. Васильєва. – К.: Видавничий дім «Освіта», 2017. – 64 с.
2. Методичні рекомендації щодо організації навчальної діяльності на уроках математики в 5 класі (система розвивального навчання Д. Б. Ельконіна – В. В. Давидова) / Г. В. Жемчужкіна, К. І. Мельник. – Х.: «Розвивальне навчання», 2010. – 52 с.
3.  Збірник задач з математики. 5-9 класи : Наскрізні лінії компетентностей та їх реалізація / Д. В. Васильєва, Н. І. Василюк. – К.: Видавничий дім «Освіта», 2017. – 112с.
4. Інтернет посилання:

«Мистецтво орігамі на уроках геометрії»

https://vseosvita.ua/library/majster-klas-mistectvo-origami-na-urokah-geometrii-386961.html

«Оригами Кубик из бумаги своими руками»

https://www.youtube.com/watch?v=lSUWtcN5qco

«Васильєва Д.В. Впровадження елементів SТEM-освіти у навчання математики»

https://www.youtube.com/watch?v=HLN36eNYWks

Навчально-дослідницька діяльність на уроках математики в контексті SТЕМ-освіти

https://www.youtube.com/watch?v=yXAwreAGjiE