Майстер-клас "Я це роблю так..."
Міністерство освіти і науки України
УО Краматорської міської ради
Краматорська ЗОШ І – ІІІ ступенів № 10 з профільним навчанням Краматорської міської ради Донецької області
МАТЕРІАЛИ ДОСВІДУ РОБОТИ
Використання прикладного програмного пакету GRAN1
на уроках математики
Автор досвіду: учитель математики
Краматорської ЗОШ І – ІІІ ступенів № 10
з профільним навчанням Краматорської міської ради
Донецької області
КУРІННА ВЕРОНІКА АНАТОЛІЇВНА
м. Краматорськ
Використання прикладного програмного пакету GRAN1
на уроках математики
(малюнки графіками функцій)
Розвиток та вдосконалення сучасних інформаційних технологій та їх поступове проникнення в освітню сферу впливає на зміст, методи, засоби навчання. Останнім часом все частіше на уроках у середній школі використовують комп’ютер, зокрема на уроках математики використовують педагогічні програмні засоби (ППЗ): Gran1, Derive. Програми можна використовувати практично на всіх заняттях математики, зокрема під час вивчення таких тем як «Поняття функції», «Перетворення графіків тригонометричних функції», «Розв’язування рівнянь та нерівностей», «Матриці і визначники» та інші.
Зазначені програми дають змогу викладачеві зробити своє спілкування з учнями ще більш інтенсивним, більше уваги приділити логічному аналізу умов задач, перекласти на комп’ютер технічні операції.
Працюючи один на один з такою програмою, учень отримує зручні умови для відпрацювання самобутніх методів, навичок і стратегій розв’язування задач, тобто має змогу виховувати в себе оригінальність думки так потрібну для розвитку евристичних та креативних моментів у мисленні .
Використання комп’ютера на уроках математики звільняє учнів від виконання рутинних обчислень, побудови графіків функцій, вивільняє час для обмірковування алгоритмів розв’язування задач, представлення результатів у більш наочній формі. Вивільнений час можна використати для більш глибокого вивчення математичної суті задачі і розв’язання їх різноманітними способами.
Використання програми GRAN1.
Одним з перших в Україні педагогічних програмних засобів був програмний комплекс для підтримки навчання математики GRAN, розробка якого розпочалася у 1989 році авторським колективом під керівництвом відомого українського вченого Мирослава Івановича Жалдака, академіка АПН України, доктора педагогічних наук, професора. Програмно-методичний комплекс GRAN, до складу
якого входять педагогічні програмні засоби GRAN1, GRAN-2D, GRAN-3D, забезпечує підтримку вивчення математики (планіметрії, стереометрії, тригонометрії, алгебри і початків аналізу, початків теорії ймовірностей і математичної статистики), а також окремих розділів фізики в школі (7–11 класи).
Розглянемо використання математичних процесорів для комп’ютерної підтримки навчання математики на прикладі програмного засобу GRAN1, який призначений для графічного аналізу функцій, що й відображає його назва GRaphic ANalysis. Запуск програми здійснюється традиційним способом: Пуск -GRAN1 - GRAN1 або з використанням ярлика . Після цього на екрані відкривається вікно програми , яке складається з трьох внутрішніх вікон: Графік, Список об’єктів, Відповіді.

У верхньому рядку вікна програми знаходиться Рядок заголовка, під
ним – Рядок меню. У програмі реалізована контекстна довідка. Для її отримання треба вибрати потрібну команду та натиснути клавішу F1. У вікні Графік будуються графічні зображення об’єктів і графіків функцій, відображаються пояснювальні написи тощо. Під час переміщення вказівника по координатній площині у вікні переміщується покажчик координат . У верхній частині вікна Графік, над робочим полем, відображаються поточні координати вказівника, у нижній частині (Рядку статусу) – максимальне та мінімальне значення координат на площині. Вікно Список об’єктів складається з двох частин. У верхній частині знаходиться поле зі списком восьми типів залежностей між змінними,
які можна обрати для побудови графічного об’єкта, а нижче – список усіх введених об’єктів, серед яких поточний об’єкт відмічено позначкою У другій частині вікна знаходяться відомості про поточний об’єкт: функція, проміжок, на якому вона розглядається, мінімальне та максимальне значення функції або інші параметри
виділеного графічного об’єкта. У вікні Відповіді подаються результати виконання різноманітних операцій, які вибираються в меню Операції – обчислення відстані від точки, обчислення довжини дуги, визначення довжини ламаної тощо. Це вікно можна очистити, виконавши Операції - Відповіді - Очистити. Зліва у вікні програми знаходиться панель інструментів.
-
 Виконання обчислень
Виконання обчислень
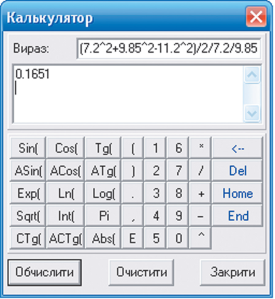
Однією з найпоширеніших функцій математичних процесорів є виконання різноманітних математичних обчислень. Програмний засіб GRAN1 має розширені можливості щодо цього.
Обчислення виконуються у вікні Калькулятор (Операції - Калькулятор). Уведення виразів можна здійснювати або з клавіатури, або використовуючи кнопки вікна Калькулятор. Після завершення введення виразу потрібно натиснути Enter або вибрати кнопку Обчислити у вікні Калькулятор. Числові вирази подаються за правилами, близькими до правил табличного процесора Excel 2007. Усі допустимі функції та операції подано на кнопках Калькулятора. Пропуски у записі виразу не допускаються. Дробова частина у записі чисел відокремлюється від цілої крапкою. Пріоритет операцій загальноприйнятий. Для його змінення використовують дужки. Редагування введеного виразу здійснюється традиційними способами.
Задача 1. Дано сторони трикутника: AB = 7,2, BC = 11,2, AC = 9,85. Обчислити міри його кутів (у радіанах).
- Побудова графіків функцій
У GRAN1 можна побудувати графіки восьми основних типів залежностей між змінними (рис. 1.8). Одночасно у вікні можна відобразити до п’яти графіків, усі вони автоматично малюються різними кольорами. Колір ліній кожного об’єкта відображається у вікні Список об’єктів біля рівняння функції.
Загальний алгоритм побудови графіка залежності між змінними:
1. Вибрати у вікні Список об’єктів тип залежності між змінними.
2. Вибрати у меню Об’єкт команду Створити.
3. Увести у поле діалогового вікна Введення виразу залежності відповідний вираз і вибрати кнопку ОК.
4. Вибрати у меню Графік команду Побудувати графік.
Розглянемо алгоритм побудови графіка функції на такому прикладі.
Задача 2. Побудувати графік функції y = |х2 – 8|x| + 7|.
- Розв’язування рівнянь і систем рівнянь графічним способом.
Розглянемо, як можна використати програмний засіб GRAN1 для графічного розв’язування рівняння з однією змінною. Алгоритм розв’язування даного типу завдань складається з трьох етапів:
1. Побудувати графік залежності.
2. Відмітити на координатній площині точку перетину графіка функції з віссю Оx.
3. Визначити координати вказівника, які відображаються у верхньому рядку вікна Графік. Це і буде наближеним коренем рівняння. Отримані у такий спосіб значення є наближеними. Похибка виникає за
рахунок того, що переміщення вказівника на Робочому полі має свій крок. Розглянемо графічне розв’язування рівнянь з однією змінною.
Задача 3. Розв’язати рівняння x3 – 2х + 6 = 0 графічним способом.
Для системи рівнянь алгоритм знаходження наближеного розв’язку виглядатиме так:
1. Побудувати графіки кожного з рівнянь системи.
2. Відмітити на координатній площині точки перетину побудованих графіків.
3. Визначити координати вказаних точок.
Задача 4. Розв’язати систему рівнянь графічним способом.
-
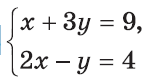
Розв’язання найпростіших задач з планіметрії
Розглянемо використання програмного засобу GRAN1 для розв’язування геометричної задачі.
Задача 5. Визначити вид чотирикутника ABCD, який задано координатами вершин A(1; 1), B(2; 3), C(0; 4), D(–1; 2). Щоб розв’язати цю задачу з використанням програми GRAN1, потрібно виконати таку послідовність дій:
1. Запустити програму GRAN1.
2. Вибрати у вікні Список об’єктів тип залежності Ламана.
3. Вибрати у меню Об’єкт команду Створити.
4. Увести в діалогове вікно Координати вершин ламаної координати вершин чотирикутника і вибрати кнопку OK.
5. Вибрати у меню Графік команду Побудувати графік.
6. Виміряти по черзі довжини сторін і діагоналей, виконавши Операції -Операції з ламаними - Довжина ламаної.
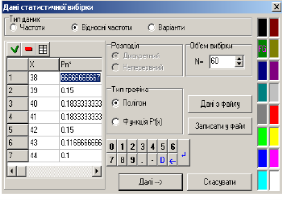
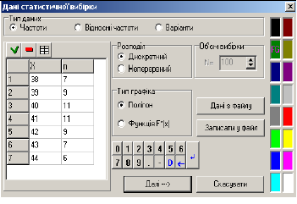
Задача 6. Для вивчення попиту на розмір чоловічих сорочок продавець записував, які розміри було продано протягом тижня. І отримав таку послідовність чисел: 38, 41, 39, 41, 44, 43, 42, 40, 39, 41, 38, 44, 43, 40, 41, 42, 38, 41, 43, 38, 44, 39, 40, 39, 42, 38, 43, 40, 41, 42, 38, 38, 43, 39, 40, 44, 42, 39, 43, 39, 44, 40, 41, 42, 39, 40, 39, 40, 44, 43, 41, 42, 40, 41, 40, 41, 42, 40, 40, 41, 42.
Необхідно побудувати ряд розподілу відносних частот та знайти числові характеристики цього ряду.
![]()
ПЛАН-КОНСПЕКТ УРОКУ АЛГЕБРИ
( З ВИКОРИСТУВАННЯМ КОМП`ЮТЕРНОЇ
ПРОГОРАМИ GRAN1 )
З ТЕМИ:” ПОБУДОВА ГРАФІКІВ ФУНКЦІЙ
ЗА ДОПОМОГОЮ ПАРАЛЕЛЬНОГО ПЕРЕНЕСЕННЯ.
КВАДРАТИЧНА ФУНКЦІЯ.”
КЛАС: 9
“Те, що я чую, я забуваю. Те, що я бачу й чую, я трохи пам‘ятаю.
Те, що я чую, бачу й обговорюю, я починаю розуміти.
Коли я чую, бачу, обговорюю й роблю, я набуваю знань і навичок.
Коли я передаю знання іншим, я стаю майстром”.
Конфуцій.
ТЕМА: ” ПОБУДОВА ГРАФІКІВ ФУНКЦІЙ ЗА ДОПОМОГОЮ
ПАРАЛЕЛЬНОГО ПЕРЕНЕСЕННЯ. КВАДРАТИЧНА ФУНКЦІЯ.”
МЕТА:
Дидактична: повторити основні відомості про функцію та її
властивості; узагальнити знання учнів про функцію.
Відпрацювати навички побудови графіків квадратичної функції,
заданої формулою y = a (x-b)2 +c .
Розвиваюча: сприяти розвитку пам`яти , уваги , логічного мислення, графічної
культури, чіткої осмисленої математичної мови, уміння аналізувати
Обладнання: комп’ютери, комп’ютерна програма GRAN1 , картки з
індивідуальними завданнями.
ХІД УРОКУ.
1.Повідомлення мети уроку.(1 хв)
2.Вступне слово вчителя .Історична довідка.(2 хв)
Функція –це одне з основних математичних та наукових понять, що виражає залежність між змінними величинами.
Поняття функції пройшло довгий еволюційний шлях. Термін “функція” вперше з`явився в 1692 році у Г.В. Лейбниця , але в більш вузькому його розумінні.
За змістом , близьким до сучасного розуміння, цей термін застосував І.Бернуллі у 1698 році. Позначення функції f(x) належить Ейлерові.
3.Актуалізація опорних знань.(5 хв)
- Що називають квадратичною функцією?
- Що є графіком квадратичної функції?
-
Як спрямовані вітки графіка квадратичної функції, якщо a
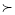 0?
0?
-
Як спрямовані вітки графіка квадратичної функції , якшо a
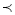 0?
0?
-
Як побудувати графік функції у= х2 + n , якщо n
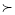 0?якщо n
0?якщо n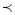 0?
0?
-
Як побудувати графік функції у= (х – m )2 , якщо m
 0?якщо m
0?якщо m 0?
0?
- Як побудувати графік функції у= (х – m )2+ n ?
4.Проведення практичної роботи .
Практична робота №1.(5 хв)
Побудувати графіки функцій за допомогою шаблона та перевірити їх за допомогою програми GRAN1 .
f(x)=х2 +3 f(x)= (х – 1 )2
f(x)= -х2 –1 f(x)= - (х + 2 )2
Практична робота №2.(10 хв)
За даними малюнком скласти формулу ,за допомогою якої задається функція, та перевірити їх правильність за допомогою програми GRAN1 .
![]()
![]() f(x)= ? у у f(x)= ?
f(x)= ? у у f(x)= ?
![]()
![]()
![]()


![]()
![]()
![]()
![]() 2
2
![]()
![]() -
-
0 х 0 х
-1
f(x)=?
![]()
![]()
![]()
![]()
![]()
![]() У у
У у
![]()
![]()
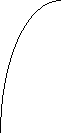

0 3 х -2 0 х
![]()
![]()
![]() у
у
![]()
![]() f(x)= ?
f(x)= ?
2
![]()
![]() 0
0
![]() х
х
![]() -2
-2
![]()
f(x)= ?
![]()
Відповіді:
f(x)= х2 –1
f(x)= - х2 +2
f(x)= (х – 3 )2
f(x)= - (х +2 )2
f(x)= (х -2 )2 -2
Практична робота №3.(20 хв)
Побудувати графік функції, виділивши квадрат двочлена із квадратного тричлена.
F(x)= х2—6х +8 f(x)= х2 +4х+4
f(x)= х2 +2х+3 f(x)= - х2 – 4х –5
Відповіді:
f(x)= (х -3 )2 -1
f(x)= (х +1 )2 +2
f(x)= (х +2 )2
f(x)= -(х +2 )2 -1
5.Підведення підсумків. Домашнє завдання.(2 хв
6. Приклади робіт учнів.
«Вишеньки»
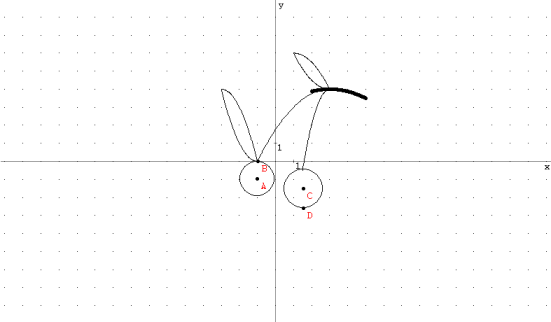
Рівняння:
- (х+1)2 +(у+1)2 =1
- (х-1,5)2 +(у+1,5)2 =1
-
у=(х+1)2 при х

-
у=-(х+3)2 +4 при х
-
у=-
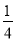 (х-3)2 +4 при х
(х-3)2 +4 при х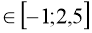
-
у=
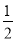 (х-3)2 +4 при х
(х-3)2 +4 при х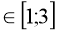
-
у= -
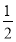 (х-1)2 +6 при х
(х-1)2 +6 при х
-
у=-2(х-3)2 +4 при х

-
у= -
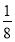 (х-3)2 +4 при х
(х-3)2 +4 при х
«Хрущ»
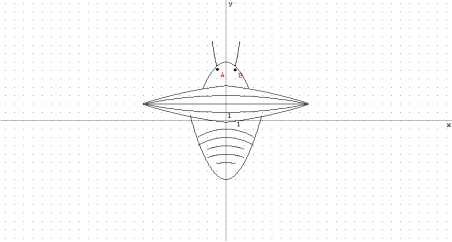
Рівняння:
-
у=
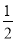 х2 -7 при х
х2 -7 при х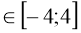
-
у= -
 х2 -7 при х
х2 -7 при х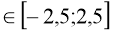
-
у=(2х-1)2 +5,5 при х
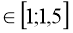
-
у=(2х+1)2 +5,5 при х
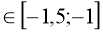
-
у= -
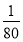 (х-5)2 +4,5 при х
(х-5)2 +4,5 при х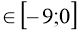
-
у=
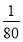 (х-5)2 -0,5 при х
(х-5)2 -0,5 при х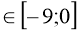
-
у= -
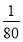 (х+5)2 +4,5 при х
(х+5)2 +4,5 при х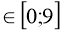
-
у=
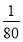 (х+5)2 -0,5 при х
(х+5)2 -0,5 при х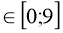
-
у= -
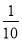 х2 -2 при х
х2 -2 при х
-
у= -
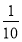 х2 -3 при х
х2 -3 при х
-
у= -
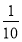 х2 -4 при х
х2 -4 при х
-
у= -
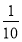 х2 -5 при х
х2 -5 при х
-
у= -
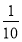 х2 -1 при х
х2 -1 при х
-
у= -
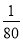 х2 +3 при х
х2 +3 при х
-
у=2 при х
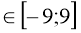
-
у=
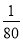 х2 +1 при х
х2 +1 при х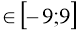
- (-1;6) 18. (1;6)
Інопланетянин

- у=x² - 2, x є [-0.5;0.5]
- у= -0.5x² + 2.5,x є [-1; 1]
- у=x² - 4, x є [-1; 1]
- у=0.5x² - 3.5, x є [-1; 1]
- D (3;1.5)
- C (-3;1.5)
- (x – 3)² + (y – 1.5)² = 4
- (x + 3)² + (y – 1.5)² = 4
- (x – 3)² + (y – 1.5)² = 1
10.(x + 3)² + (y – 1.5)² = 1
11.у= - 0.15x² + 4.9, x є [-3;3]
12.A (-4;7.3)
13.B (4;7.3)
14.у= -(x +3)²+ 8.3, x є [-4;- 1]
15.у=( -x – 3)²+ 8.3, x є [-1;- 4]
16. у=0.5x² - 5, x є [-2,8; 2,8]
«Корабель»
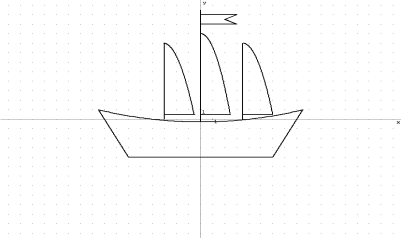
Рівняння:
-
у=-4 х
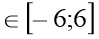
-
у=1 х
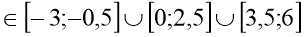
-
у=10 х
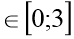
-
у=11 х
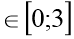
-
у=
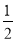 х+9,5 х
х+9,5 х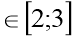
-
у= -
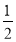 х+11,5 х
х+11,5 х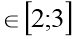
-
х=0 у
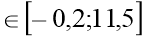
-
х=-3 у
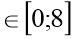
-
х=3,5 у
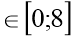
-
у=-2х-16 х

-
у=2х-16 х
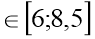
-
у=
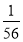 х2 -0,3 х
х2 -0,3 х 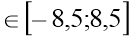
-
у=-1,3х2 +9 х

-
у=-
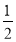 (х-3,5)2 +8 х
(х-3,5)2 +8 х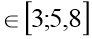
-
у=-
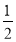 (х+3)2 +8 х
(х+3)2 +8 х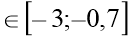
«Сніговик»
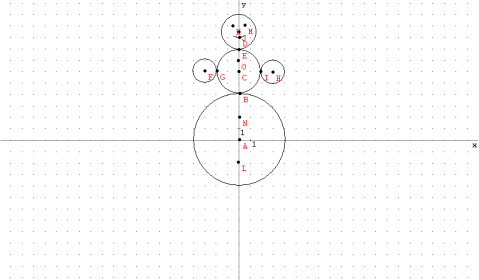
Рівняння:
- х2 +у2 =16
- х2 +(у-6)2 =4
- х2 +(у-9,5)2 =2.25
- (х-3)2+(у-6)2 =1
- (х+3)2+(у-6)2 =1
-
у=0,5х2 +9 х
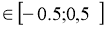
- (-0.5;10)
- (0.5;10)
- (0;2)
- (0;-2)
- (0;7)
Висновок
Комп’ютерні програми згаданого типу можуть бути використані практично на всіх уроках математики, починаючи вже з п’ятих-шостих класів, зокрема під час вивчення системи на прямій і на площині, поняття функції, елементарних функцій та їхніх властивостей, методів розв’язування рівнянь і нерівностей та їхніх систем, елементів теорії границь числових послідовностей, диференціального та інтегрального числень та їх застосуванні, при вивченні курсу стереометрії.
Використання інтерактивних технологій – не самоціль. Це лише спосіб створення такої атмосфери в класі, яка найкраще сприяє співпраці, порозумінню та доброзичливості, дає змогу по-справжньому реалізувати особистісне орієнтоване навчання.
Література
- Жалдак М.І., Горошко Ю.В., Вінниченко Є.Ф. Математика з комп’ютером. Посібник для вчителів. – К. РННЦ ДІНІТ, 2004.
- Жалдак М.І., Михалін Г.О. Елементи стохастики з комп’ютерною підтримкою. Посібник для вчителів. – К: Шкільний світ, 2002.
- Жалдак М.І. Gran1 – математика для всех. //Компьютеры + программы. – 1995. – №5(20). – с.72-76
- Жалдак М.І. Комп’ютер на уроках математики: Посібник для вчителів. – К., Техніка, 1997. – 304 с.
- Жалдак М.І., Михалін Г.О. Елементи стохастики з комп’ютерною підтримкою. Посібник для вчителів. – К: Шкільний світ, 2002.
1

про публікацію авторської розробки
Додати розробку
