Урок-лекція. Об’єми тіл обертання: циліндра, конуса, кулі та її частин.

Навчальний модуль

Об’єми та площі поверхонь

геометричних тіл

Геометрія 11 клас

  Підготувала вчитель математики

Яблунського ліцею

Солотвинської селищної ради

 Костур Дарія Дмитрівна

Конспект №3

Урок-лекція (2 год)

Тема модуля.  Об’єми тіл обертання: циліндра, конуса, кулі та її частин.

Мета модуля:  Домогтися засвоєння формул для обчислення об’ємів тіл обертання: циліндра, конуса, кулі та її частин. Сформувати вміння розв’язувати задачі на обчислення об’ємів за допомогою вивчених формул. Виховувати працьовитість, спостережливість, уважність.

Тип модуля:  Змістово-пошуковий.

Обладнання:  моделі тіл обертання (циліндра, конуса, кулі); мультимедійна дошка, міні-підручники.

Хід уроку

І. Повідомлення теми та мети уроку.

ІІ. Аналіз самостійної роботи.

Повідомити загальний результат виконання роботи та проаналізувати її.

ІІІ. Цілепокладання.

Виконання усних вправ

За допомогою проектора задачі проектую на дошку.

1.   Осьовим перерізом циліндра є квадрат, діагональ якого дорівнює 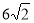см. Чому дорівнюють висота і радіус цього циліндра?
2.   Діагональ осьового перерізу циліндра дорівнює 8 см і утворює кут 60^о із площиною основи циліндра. Обчисліть площу основи циліндра.
3.   Переріз циліндра перетинає його основу по хорді завдовжки 3 см, яку видно з центра основи під кутом 60^о. Обчисліть площу основи циліндра.
4.   Висота конуса дорівнює 3 см, а його твірна – 5 см. Чому дорівнює площа основи конуса?
5.   Довжина кола основи конуса дорівнює 12π см, а твірна конуса –       10 см. Чому дорівнює висота конуса?
6.   Площа великого круга кулі дорівнює 9π см². Чому дорівнює діаметр кулі?
7.   Площа перерізу кулі площиною, віддаленою від її центра на 6 см, дорівнює 64π см². Чому дорівнює радіус кулі?

Перший міні-модуль

1.   Формула для обчислення об’єму циліндра.
2.   Приклади застосування формули для обчислення об’єму циліндра.

Другий міні-модуль

1.     Формула для обчислення об’єму конуса.

2.   Формула для обчислення об’єму зрізаного конуса.
3.   Приклади застосування формули для обчислення об’ємів конуса та зрізаного конуса.

Третій міні-модуль

1. Формула для обчислення об’єму кулі.
2.   Означення кульового сегмента та його елементів.
3.   Формула для обчислення об’єму кульового сегмента.
4.   Означення кульового сектора та його елементів.
5.   Формула для обчислення об’єму кульового сектора.
6.   Приклади застосування формули для обчислення об’ємів кулі та її частин.

IV. Сприйняття та усвідомлення нового матеріалу.

1.   Пояснення матеріалу про об’єми циліндра, конуса, кулі та її частин проводжу так, як це зроблено в п.п. 73-78 §8 підручника [5].
2.   Учні записують довідник вивчених формул у міні-підручниках.

Об’єми тіл обертання

– об’єм циліндра

– об’єм конуса

– об’єм зрізаного конуса, де h – висота зрізаного конуса, R₁ і R₂ – радіуси відповідно нижньої і верхньої основ зрізаного конуса

– об’єм кулі

Кульовим сегментом називається частина кулі, яку відтинає від неї січна площина.

– об’єм кульового сегмента, де R – радіус кулі, H – висота кульового сегмента.

Кульовим сектором називається тіло, яке дістають з кульового сегмента і конуса таким чином. Якщо кульовий сегмент менший за півкулю, то кульовий сегмент доповнюють конусом, у якого вершина знаходиться в центрі кулі, а основою є основа сегмента. Якщо ж сегмент більший від півкулі, то згаданий конус із нього вилучається. Об’єм кульового сектора дістаємо додаванням або відніманням об’ємів відповідних сегментів і конуса.

– об’єм кульового сектора, де R – радіус кулі, H – висота відповідного кульового сегмента.

3.   Розв’язування задач з підручника [5].

Задача №6 (с. 119)

Свинцева труба (густина свинцю 11,4 г/см³) з товщиною стінок 4 мм має внутрішній діаметр 13 мм. Яка маса 25 м цієї труби?

Розв’язання

, де V – об’єм свинця.

, де V₁ і V₂ – об’єми зовнішнього та внутрішнього циліндрів відповідно.

(мм).

Об’єми циліндрів дорівнюють:

, .

Визначимо об’єм свинця, враховуючи, що D₁=2,1 см, D₂=1,3 см,      l=2500 см.

(см³).

Обчислимо масу труби: .

.

Задача №10 (с. 119)

Твірна конуса l утворює з площиною основи кут α. Знайдіть об’єм конуса.

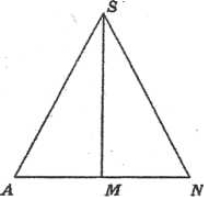
Проведемо осьовий переріз. Це рівнобедрений ASN з кутом α при основі.

Із ASN: , .

Визначимо об’єм конуса:

.

.

Задача №27 (с. 120)

Площина, перпендикулярна до діаметра кулі, ділить його на частини 3 см і 9 см. На які частини ділиться об’єм кулі?

Площина, перпендикулярна діаметру, відтинає сегмент з висотою 3 см.

Об’єм сегмента обчислимо за формулою:

.

Радіус кулі дорівнює (см).

Тоді (см³).

Об’єм кулі дорівнює:

(см³).

Тоді об’єм другого сегмента дорівнює:

(см³).

Площина розбиває кулю на сегменти об’ємами і .

V. Домашнє завдання

§8, п.п. 73-78; контрольні запитання 1-6; задачі №1, 7, 22 (с. 119-120).

VІ. Підсумок лекції

За допомогою мультимедійного проектора проектую на дошку запитання до класу.

1.   Чому дорівнює об’єм циліндра?
2.   Об’єм циліндра дорівнює 250π см³, а висота – 10 см. Укажіть, які з наведених тверджень правильні, а які – неправильні:

а) об’єм циліндра дорівнює добутку площі основи на висоту;

б) площа основи циліндра дорівнює 25 см²;

в) радіус циліндра дорівнює 10 см;

г) радіус циліндра вдвічі менший від твірної циліндра.

3.   Чому дорівнює об’єм конуса?
4.   Дано конус, у якого радіус основи ОА=8 см і висота SO=15 см. Укажіть, які з наведених тверджень правильні, а які – неправильні:

а) катети прямокутного трикутника SOA дорівнює 17 см і 8 см;

б) осьовим перерізом конуса є прямокутний трикутник із гіпотенузою SA=17 см;

в) твірна конуса дорівнює 15 см;

г) об’єм конуса дорівнює см³.

5.   Чому дорівнює об’єм кулі?
6.   Знайти об’єм кулі, діаметр якої 12 см.
7.   Об’єм кулі дорівнює 36π см³. Знайти радіус кулі.

Література

1. Пєхота О.М. Сучасні освітні технології. – К., А.С.К., 2001.
2. Смишляєва В.К. У світі математики. – К.; Рад. шк., 1976. – Випуск   7. – с. 183.
3. Пометун О., Пироженко Л. Сучасний урок. – К.: А.С.К., 2003.
4. Істер О.С., Глобін І.Є., Панкратова І.Є. Збірник завдань для державної підсумкової атестації з математики. – Київ.: ЦНМЛ, 2011.
5. Погорєлов О.В. Геометрія: Стереометрія: Підруч. Для 10-11 кл. серед. шк. К.: Освіта, 1998.
6. Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: Стереометрія: Підруч. Для 11 кл загальноосвітніх навчальних закладів. – К.: «Генеза», 2011.
7. Погорєлов О.В. Геометрія: Планіметрія: Підручник для 7-9 кл. загальноосвітніх навчальних закладів. – К.: Школяр, 2004.