Урок-практикум. Розв’язання базових задач. Самостійна робота

 

 

 

 

 

 

Навчальний модуль

 

Об’єми та площі поверхонь

геометричних тіл

 

 

 

Геометрія 11 клас

 

 

 

 

  Підготувала вчитель математики

Яблунського ліцею

Солотвинської селищної ради

 Костур Дарія Дмитрівна

 

 

Конспект №2

 

Урок-практикум (2 год)

 

Тема модуля.  Розв’язання базових задач. Самостійна робота.

 

Мета модуля:  Формувати навички розв’язування задач на знаходження об’ємів паралелепіпеда, призми, піраміди; розвивати вміння застосовувати формули об’ємів; виховувати творче мислення та просторову уяву учнів.

 

Тип модуля:  контрольно-смисловий.

 

Обладнання:  мультимедійний проектор, моделі геометричних фігур, міні-підручник.

 

Хід уроку

 

І. Організаційний момент

 

ІІ. Мотивація навчальної діяльності учнів

 

Для зацікавлення учнів, розвитку інтересу до вивченого матеріалу пропоную розв’язати такі практичні задачі.

На дошку проектую задачі.

 

Задача 1. Знайти об’єм повітря у класній кімнаті, довжина якої 8 м, ширина 6м, висота 2,5 м.

 

Задача 2. У басейні з горизонтальним дном і площею 1 га міститься        1 мільйон літрів води. Чи можливо в цьому басейні проводити змагання з плавання?

(Об’єм води в басейні 1 000 000 л =1 000 м³, площа основи басейна

Отже, висота басейна

І змагання в ньому проводити неможливо.)

 

ІІІ. Актуалізація опорних знань і опитування учнів.

 

1.     Перевірка рівня осмислення теоретичних знань (учні, об’єднавшись у групи, проводять взаємоопитування).

Запитання

1. Сформулювати основні властивості об’єму.
2. Чому дорівнює об’єм прямокутного паралелепіпеда?
3. Що таке одиничний куб?
4. За якою формулою обчислюється об’єм будь-якої призми?
5. Сформулювати задачу-теорему про об’єм похилої призми.
6. Чому дорівнює об’єм прямої призми?
7. Чому дорівнює об’єм будь-якої піраміди?
8. Як відносяться об’єми подібних фігур?

 

2. Перевірка домашнього завдання.

Відповіді на запитання, що виникли під час розв’язання домашнього завдання.

 

 

IV. Розв’язування задач.

 

1.   «Перевір себе». Задача №12 з підручника [5] с. 109.

У прямому паралелепіпеді сторони основи і утворюють кут . Менша діагональ паралелепіпеда дорівнює . Знайти його об’єм.

Розв’язання

 

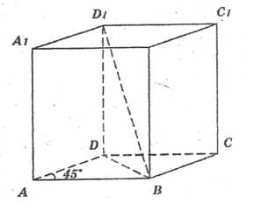
За умовою: ; ; .

Об’єм паралелепіпеда дорівнює:

, де H – висота; S – площа основи або: ;

.

Площа основи дорівнює:

.

Із .

BD знайдемо з АВD за теоремою косинусів:

.

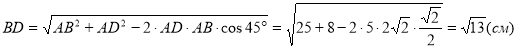Тоді .

Обчислимо об’єм: .

.

 

 

2.   «Коло ідей». Задача №16* з підручника [5] с. 109.

Грані паралелепіпеда – рівні ромби із стороною а і гострим кутом 60^о. Знайдіть об’єм паралелепіпеда.

 

 

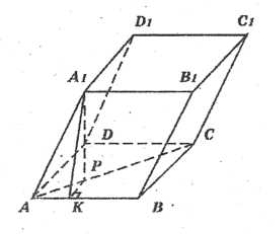
Пояснення до рисунка

З точки А₁ опустимо перпендикуляр на площину основи. Проведено А₁КАВ. За теоремою про три перпендикуляри РКАВ.

Розв’язання

Об’єм паралелепіпеда дорівнює:

.

Площа основи дорівнює:

.

.

З АА₁Р за теоремою Піфагора: .

Знайдемо АР. З АА₁К: .

Діагональ ромба є гіпотенузою кута при вершині. Тому РАК=30^о.

З АРК .

Знайдемо А₁Р.

.

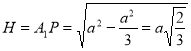Об’єм паралелепіпеда дорівнює: .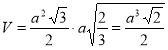

.

 

3.   «Знайти позицію». Задача №28 з підручника [5] с. 111.

У прямій трикутній призмі сторони основи дорівнюють 4 см, 5 см і 7 см, а бічне ребро дорівнює більшій висоті основи. Знайдіть об’єм призми.

Розв’язання

Об’єм призми дорівнює:

Площу основи знаходимо за формулою Герона:

.

За умовою, Н дорівнює більшій висоті основи. Отже, Н дорівнює висоті, проведеній до меншою сторони основи.

Менша сторона, у нашому випадку, дорівнює 4 см.

Виразимо площу основи через меншу сторону та висоту:

або

, звідси

.

Обчислимо об’єм: .

Відповідь: .

 

4.   «Будь уважним». Задача №45 з підручника [5] с. 112.

У піраміді з площею Q₁ проведено переріз паралельно основі, на відстані h від неї. Площа перерізу дорівнює Q₂. Знайдіть висоту піраміди.

Розв’язання

 

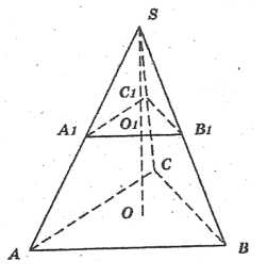
Переріз, паралельний основі, відтинає піраміду, подібну даній.

Отже, , .

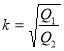Висота більшої піраміди дорівнює Н. Висота меншої піраміди дорівнює . Тоді, із подібності пірамід, можна записати:

або .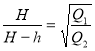

Зробимо перетворення:

.

.

.

.

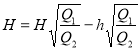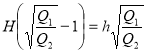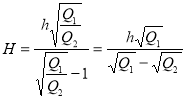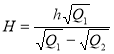5.   «Хто швидше». Задача №49 з підручника [5] с. 112.

Висота піраміди h. На якій відстані від вершини знаходиться переріз, який паралельний основі і ділиться її об’єм навпіл?

Розв’язання

Переріз, паралельний основі, відтинає подібну піраміду. Отже,

.

Тоді .

Із подібності пірамід витікає: , звідси .

 

 

V. Самостійна робота

 

Для початкового та середнього рівнів навчальних досягнень самостійну роботу проводжу за допомогою тесту.

 

Початковий та середній рівні навчальних досягнень

 

Варіант 1

1. Кожне ребро куба збільшили на 2 см. На скільки збільшився його об’єм?

А) На 8 см³;

Б) на 2 см³;

В) на 4 см³;

Г) визначити неможливо.

2. Основою призми є прямокутний трикутник, катети якого дорівнюють 6 см і 8 см. Висота призми дорівнює 10 см. Обчисліть об’єм призми.

А) 360 см³;

Б) 120 см³;

В) 40 см³;

Г) 240 см³.

3. Основою піраміди є ромб, діагоналі якого дорівнюють 6 см і 8 см. Висота піраміди дорівнює 16 см. Обчисліть об’єм піраміди.

А) 768 см³;

Б) 384 см³;

В) 256 см³;

Г) 128 см³.

 

Варіант 2

1. Кожне ребро правильного тетраедра збільшили на 2 см. На скільки збільшився його об’єм?

А) На 8 см³;

Б) на 2 см³;

В) на 4 см³;

Г) визначити неможливо.

2. Основою прямої призми є ромб, діагоналі якого дорівнюють 6 см і       8 см. Бічне ребро призми дорівнює 20 см. Обчисліть об’єм призми.

А) 360 см³;

Б) 240 см³;

В) 960 см³;

Г) 480 см³.

3. Сторона основи правильної трикутної піраміди дорівнює 10 см. Обчисліть об’єм піраміди, якщо її висота дорівнює 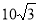см.

А) 1000 см³;

Б) 750 см³;

В) 250 см³;

Г)  см³.

 

Достатній та високий рівні навчальних досягнень

 

Варіант 1

1. Довжина діагоналі прямокутного паралелепіпеда більша від його вимірів на 20 см, 9 см і 5 см. Обчисліть об’єм паралелепіпеда.
2. У правильній трикутній призмі радіус кола, описаного навколо основи, дорівнює 2 см, а діагональ бічної грані – 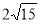см. Обчисліть об’єм призми.
3. У правильній чотирикутній піраміді двогранний кут при ребрі основи дорівнює α. Знайдіть об’єм піраміди, якщо її бічне ребро дорівнює l.

 

Варіант 2

1. Довжина бічного ребра прямокутного паралелепіпеда дорівнює 6 см, довжина діагоналі паралелепіпеда удвічі менша від периметра основи. Обчисліть об’єм паралелепіпеда.
2. У правильній чотирикутній призмі радіус кола, описаного навколо основи, дорівнює 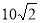см, а діагональ бічної грані – 25 см. Обчисліть об’єм призми.
3. У правильній трикутній піраміді плоский кут при вершині дорівнює α. Знайдіть об’єм піраміди, якщо її висота дорівнює h.

 

 

VІ. Підсумок практичного заняття

 

 

Домашнє завдання:

1. задачі №№1166, 1187 з підручника [6];
2. повторити: п.п. 38-41 (7 клас), 116, 119 (9 клас) з підручника [7]; п.п. 19, 32, 33 (10 клас), §6 (11 клас) з підручника [5].

 

 

 

 

 

 

Література

 

1. Пєхота О.М. Сучасні освітні технології. – К., А.С.К., 2001.
2. Смишляєва В.К. У світі математики. – К.; Рад. шк., 1976. – Випуск   7. – с. 183.
3. Пометун О., Пироженко Л. Сучасний урок. – К.: А.С.К., 2003.
4. Істер О.С., Глобін І.Є., Панкратова І.Є. Збірник завдань для державної підсумкової атестації з математики. – Київ.: ЦНМЛ, 2011.
5. Погорєлов О.В. Геометрія: Стереометрія: Підруч. Для 10-11 кл. серед. шк. К.: Освіта, 1998.
6. Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: Стереометрія: Підруч. Для 11 кл загальноосвітніх навчальних закладів. – К.: «Генеза», 2011.
7. Погорєлов О.В. Геометрія: Планіметрія: Підручник для 7-9 кл. загальноосвітніх навчальних закладів. – К.: Школяр, 2004.