Метод інтервалів для розв'язування тригонометричних рівнянь

3.2.3 Метод інтервалів.

Основою методу є твердження,що якщо тригонометрична функція y = ƒ(x) визначена та неперервна на деякому проміжку X і не має корені в на цьому  проміжку.

Тому,щоб розв’язати нерівність ƒ(x)>0 або ƒ(x)<0,де ƒ(x)- тригонометрична функція,потрібно

1.Знайти область визначення D(ƒ ) та період T  функції ƒ(x);

2.Замінити знак нерівності на знак рівності і розв’язати відповідне тригонометричне рівняння на проміжку, який має довжину періоду T;

3.На числовій осі відмітити проміжок,який має довжину періода T,розбити його точками розриву ф-ції ƒ(x) і коренями рівняння ƒ(x) = 0 на інтервали,на яких ф-ція зберігає свій знак;

4.Методом пробних точок відбираємо інтервали розв’язків нерівності на вибраному проміжку;

5.Провести відбір для характерних точок нерівності-коренів рівняння ƒ(x) = 0 і кінців проміжків ОДЗ.Якщо початкова нерівність строга,то корені ƒ(x) = 0 не є коренями нерівності,у іншому випадку-є;

6.З урахуванням періодичності ф-ції знаходимо розв’язки на всій числовій прямій.

Проілюструємо,те що написано вище прикладом.

Приклад 1.Розв’язати нерівність cos 2x ctg x < 0

Розв’язання.Наша ф-ція ƒ(x) = cos 2x ctg x визначена та неперервна на множині всі дійсних чисел,крім чисел вигляду πl, l – цілі числа.

Період функції ƒ(x) = cos 2x ctg x дорівнює π,бо період cos 2x ctg x теж дорівнює π.

Знайдемо нулі функції cos 2x ctg x =0.

                                                          ,де n,m – цілі числа.

Розглянемо проміжок [;,його довжина дорівнює періоду.

На ньому функція не визначена в точці 0 і має нулі в точках ,,.

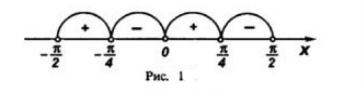
Визначаємо знак на кожному інтервалі (рис.1)

З урахуванням періодичності ƒ(x) маємо

(k) ∪ (),k – цілі числа