Методи розв'язування задач на розфарбовування
Про матеріал
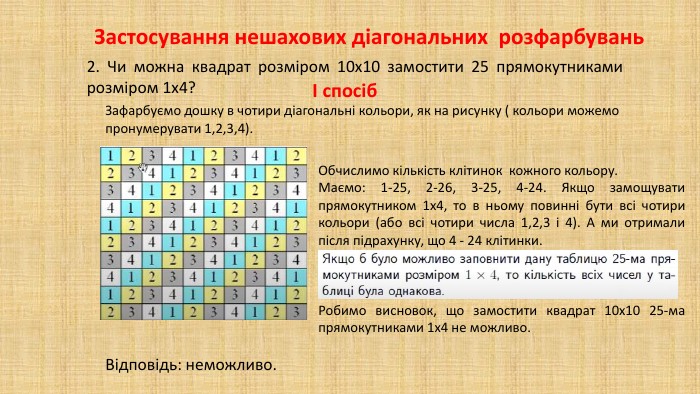
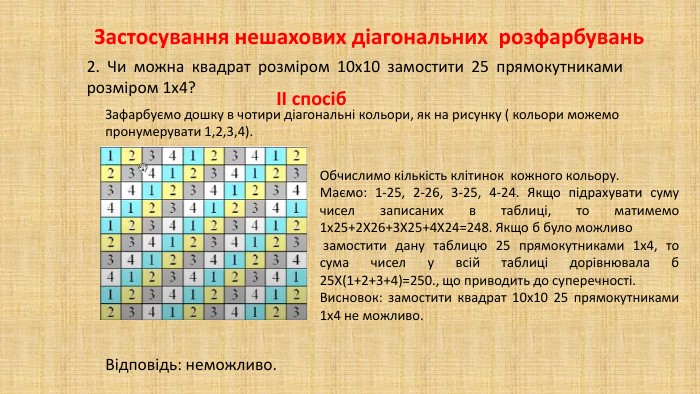
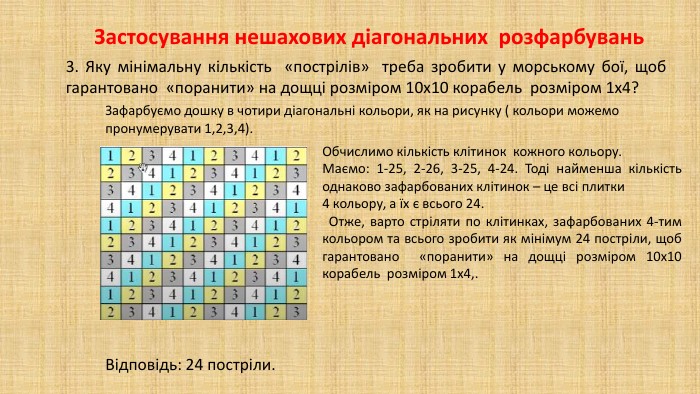
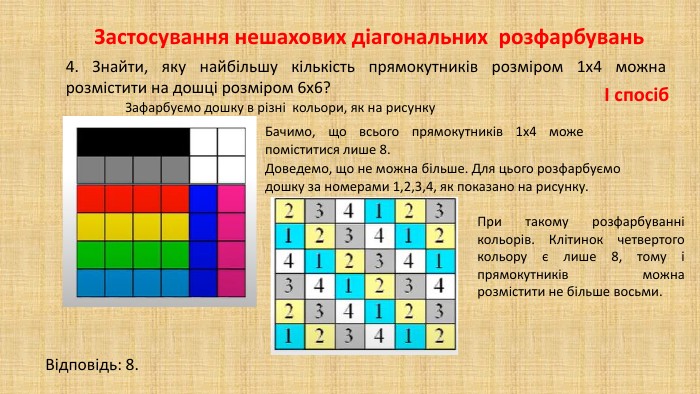
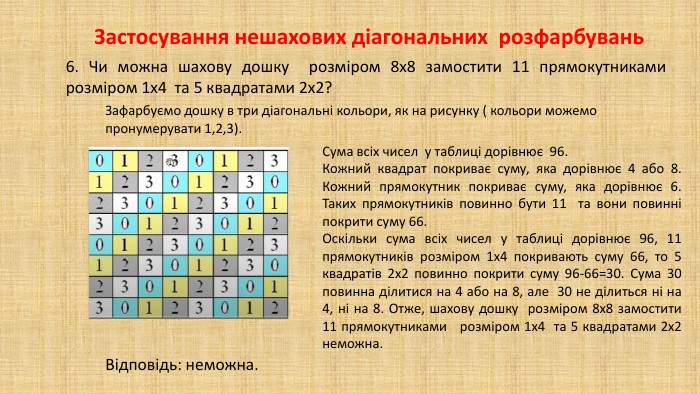
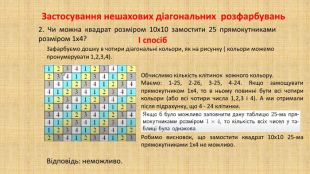
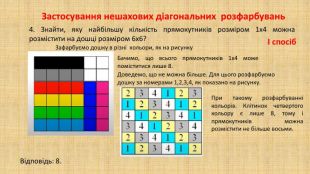
В презентації "Методи розв'язування задач на розфарбовування" дібрано низку цікавих олімпіадних задач при розв'язуванні яких використовується інформація про загальні методи розв'язування задач на розфарбовування клітчастих дошок.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку