Методичка "Математичні кросворди та ребуси"

Про матеріал

На сучасному етапі розвитку нашого суспільства першочерговим завданням школи є виховання всебічно розвиненої людини. Важливою складовою цього завдання є боротьба за високу якість знань і вмінь учнів, формування в них навичок самостійної розумової праці, виховання творчої особистості. Кожен учитель прагне зацікавити учнів предметом, який він викладає, бо це є запорукою успішного навчання. Таке завдання, безсумнівно, ставлять перед собою і вчителі математики. «Зацікавити розум дитини – ось що є одним з основних положень нашої доктрини, і ми нічим не нехтуємо, щоб прищепити учневі смак, ми б сказали, навіть пристрасть до навчання», − вважав видатний математик М. Остроградський. Одним із засобів зацікавлення учнів математикою є добре продуманий урок та позакласна робота. Використання на уроках різних ігор, кросвордів, ребусів, головоломок дають можливість ширше пропагувати досягнення і значення математичної науки, прищепити учням любов до математики, сприяти виявленню і розвитку здібностей учнів, а також глибшому засвоєнню ними програмного матеріалу. На заняттях можна організовувати розв’язування дещо складніших і цікавих задач, що розвивають кмітливість і математичне мислення.

Перегляд файлу

Міністерство освіти і науки України

Відділ освіти Локачинської райдержадміністрації загальноосвітня школа І-ІІІ ступеня с. Бубнів

М. А. Юхно

УДК 373.5.031

ББК 74.202.20

Юхно М. А. Математичні кросворди та ребуси. Методичні рекомендації – Луцьк: ПВД «я», 2016. – 120 с.

У методичних рекомендаціях міститься поради, кросворди, ребуси, дидактичні матеріали, цікаві завдання для учнів 5-11 класів. Для вчителів математики загальноосвітніх шкіл.

Рецензенти:

Трачук Т.В. - доцент кафедри теорії та методик викладання шкільних предметів ВІППО, кандидат педагогічних наук

Комар О.С. – головний спеціаліст відділу освіти Локачинської райдержадміністрації.

Запропонована методична розробка становить інтерес для вчителів математики. Вона містить цікаві кросворди та ребуси , які можуть бути використані як на уроках, так і в позакласній роботі: при проведенні шкільних олімпіад, конкурсів, турнірів, математичних боїв. Даний посібник сприяє розширенню математичного кругозору учнів.

Схвалено на засіданні методичної ради Локачинського райметодкабінету Протокол № 4 від 29.12. 2015 р.

ЗМІСТ

ВСТУП...……………………………………………………………………….....4

МАТЕМАТИЧНІ КРОСВОРДИ

Використання кросвордів на уроках математики як засіб розвитку пізнавальних інтересівучні……….……………………………………....6 Математика в кросвордах ……………………………………………….15

МАТЕМАТИЧНІ РЕБУСИ

Історія математичних ребусів ………………………………………....72

Як розв’язувати математичні ребуси …………………………………75

Математичні ребуси .………………………………………………….….77

ФРАГМЕНТИ УРОЧНОЇ ТА ПОЗАУРОЧНОЇ РОБОТИ Розробки уроків ……………………………………………………..…89

Фрагменти проведення тижня математики ……………………………..99

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ……………………………..…115

ВСТУП

Кожен учитель прагне зацікавити учнів предметом, який він викладає, бо це є запорукою успішного навчання. Таке завдання, безсумнівно, ставлять перед собою і вчителі математики.

«Зацікавити розум дитини – ось що є одним з основних положень нашої доктрини, і ми нічим не нехтуємо, щоб прищепити учневі смак, ми б сказали, навіть пристрасть до навчання», − вважав видатний математик М.

Остроградський.

Одним із засобів зацікавлення учнів математикою є добре продуманий урок та позакласна робота.

Використання на уроках різних ігор, кросвордів, ребусів, головоломок дають можливість ширше пропагувати досягнення і значення математичної науки, прищепити учням любов до математики, сприяти виявленню і розвитку здібностей учнів, а також глибшому засвоєнню ними програмного матеріалу. На заняттях можна організовувати розв’язування дещо складніших і цікавих задач, що розвивають кмітливість і математичне мислення. Велике виховне значення має позакласна робота з математики. Конкурси, вікторини, турніри, інтелектуальні змагання виховують бажання глибше пізнати цікавий світ математики, товариськість, толерантне ставлення до суперників, прагнення самовдосконалюватися та не зупинятися на досягнутому. Важливим елементом роботи вчителя є проведення тижня математики.

В усі часи для розвитку людини мало велике значення уміння збирати необхідну інформацію, вміння висувати гіпотезу, робити висновки, розробляти власні стратегії поведінки. Збільшення об’єму інформації призводить до того, що з кожним роком збільшується розрив між загальною кількістю наукових знань і тієї їх частиною, яка засвоюється в навчальному закладі. Сучасний учень повинен вміти адаптуватися в різних життєвих ситуаціях, самостійно набувати систему необхідних предметних знань для вирішення практичних завдань. Молода людина, яка не володіє сучасними ІКТ, яка не ознайомилася з технологіями Інтернет у ЗНЗ, буде неминуче відкинута за межі сучасного інформаційного суспільства.

У зв'язку з цим пріоритетним завданням педагогів є не передача готових знань, а навчання способів пошуку, зберігання, вибору, обробки інформації та її використання. Самоосвіта у сучасному суспільстві є основою освіти і фундаментом для розвитку особистості. Завдяки інформаційним технологіям ці завдання можна досить успішно розв’язувати.

Інформаційні технології широко впроваджуються у навчальний процес. Насамперед як засіб доступу до інформації, індивідуалізації та диференціації навчання. Їх можна використовувати при ознайомленні учнів з новим матеріалом і для закріплення та повторення вивченого. Уроки математики відрізняються від інших своєю специфікою: мало теорії, багато практики і основними інструментами залишаються зошит і ручка. Можна весь урок переглядати презентації, відео, слухати цікаві факти, але поки сам не почнеш розв’язувати на папері – результат не буде високим. В той же час для підтримки інтересу учнів до математики, для різноманітності інформації, для того, щоб урок був яскравим, насиченим і нетрадиційним, просто необхідно використовувати інформаційні технології, пам’ятаючи при цьому про міру і доцільність їх застосування.

У цій книзі вміщено дидактичний матеріал, який учитель може використати при проведенні уроків, конкурсів, позакласних заходів, зокрема, кросворди, ребуси, цікаві задачі.

Сподіваюся, що ця книга стане цікавою і корисною читачам.

МАТЕМАТИЧНІ КРОСВОРДИ

Використання кросвордів на уроках математики як засіб розвитку пізнавальних інтересів учнів

Математична задача іноді така ж цікава, як кросворд, і напружена розумова робота

може бути настільки ж бажаною вправою, як стрімкий теніс Д. Пойа

Зараз навряд чи хтось згадає і замислиться про того, хто був піонером у складанні кросвордів. Дивно і те, що вже багато років ця гра живе, росте, розвивається і видозмінюється. Кросворд має унікальну властивість дати можливість проявити себе, дозволяє самостійно відшукувати відповіді на поставлені питання, пізнавати світ на інтуїтивному рівні. Використання кросвордів дозволяє індивідуально та диференційовано підходити до учнів на уроці. Школярі за власним бажанням починають звертатися за допомогою до підручників, додаткових посібників та іншої літератури й Інтернету.

Розв’язування кросвордів - це своєрідна «гімнастика розуму». Ігри такого роду корисні в будь-якому віці. Вони розвивають і тренують пам’ять, загострюють догадливість, виробляють настирливість, здатність логічно думати, аналізувати, порівнювати, виробляти вміння орієнтуватись в світі сучасної наукової інформації.

Кросворд (з англійського «cross» – перетин і «word» – слово) – завдання-головоломка, основана на заповненні рядків, що перетинаються, клітинок (за вертикаллю і горизонталлю) словами. Інакше кажучи, щоб розгадати кросворд, потрібно визначити слово за його характеристикою і в кожну білу клітинку фігури, починаючи з пронумерованої, вписати по одній літері. Закінчується слово заштрихованою клітинкою або краєм фігури.

У своїй діяльності ми широко використовую кросворди. Власна практика показала, що використання кросвордів розширює світогляд, розвиває логічне мислення і пам’ять.

Кросворди складають і самі учні, застосовуючи в процесі цього Microsoft Word, Microsoft Excel, Microsoft PowerPoint.[ 10 ]

Математика як навчальний предмет має необхідні передумови для розвитку пізнавальних процесів школярів.

На уроках математики в результаті взаємодії зусиль учителя і учнів розвивається елементарне математичне мислення учнів, створюються умови для корекції пам’яті, уваги, мови. Пояснюючи навчальний матеріал на уроках математики, широко використовуються математичні терміни, специфічні словосполучення, котрі на інших уроках і в повсякденному житті дуже рідко зустрічаються. Учні відчувають значні труднощі в розумінні, запам’ятовуванні, вимові та застосуванні незвичних для них слів. Учителю необхідно працювати над тим, щоб за кожним словом і терміном стояв конкретний образ, щоб учні включали нові слова, геометричні та математичні терміни у свій активний словник.

До багатьох факторів, що впливають на процес запам’ятовування учнями навчального матеріалу, відноситься і спосіб його сприйняття. Багатьма вченими доведено, що учні краще запам’ятовують той матеріал, подання якого відбувається за допомогою використання різних допоміжних засобів і методів (картинок, схем, ребусів, кросвордів і т. д.)

Одним із методів, що сприяють активізації запам’ятовування математичних термінів, є застосування кросвордів, ребусів та цікавих задач на уроках математики.

Особливе значення для продуктивності запам’ятовування має те, в якій формі воно відбувається. Довільне запам’ятовування відбувається незаплановано, без спеціальної мети запам’ятати. Людина краще запам’ятовує те, що відповідає її інтересам, мотивам, запитам. Застосування ребусів та кросвордів підвищує інтерес до навчальної діяльності,а сам процес розгадування стає цікавим для учнів. Запам’ятовування математичних термінів відбувається немов би саме по собі, довільно, в результаті вольової і розумової діяльності школярів під час розв’язування кросвордів, ребусів.

Кросворди навчають без дидактичності, вони, при всій традиційності свого змісту, оригінальні і направлені на досягнення важливої мети – пробудження в учнів самостійного і нестандартного мислення та любові до математики. Все почалося з

математики При створенні кросвордів з математики не

Вже в обов’язково дотримуватися симетрії в розміщенні

стародавній

клітиночок для вписування слів. Важливо

Месопотамії, майже

п'ять тисяч років використати ідею цієї гри для включення учнів в тому, складали і активну розумову діяльність. Запропоновані учням

вирішували

достатньо складні кросворди складені за окремими темами програми, задачі алгебри на визначення невідомої але вони можуть мати і завдання із різних тем.

величини. Пізніше в Нескладні за формою і змістом – включають від 5 до Давньому Єгипті

з'явилися перші 10 слів. Розв’язування кросвордів доступне учням, але

задачники. завдання в міру складні, змушують їх думати над

Шотландський

єгиптолог Хінд відповідями.

знайшов папірус,

Дані кросворди використовуються при

датований XVII

століттям до нашої повторенні та закріпленні матеріалу, у фронтальній та ери, присвячений індивідуальній роботі з учнями на різних етапах

математиці. Він є

сувоєм завдовжки уроку. До одного і того ж кросворду картки із близько п'яти з

половиною метрів і завданнями можна складати по-різному. Завдання

шириною близько може бути дано в зоровій формі з посиланням на п'ятнадцяти

сантиметрів. Писар наочність і використовуватися при первинному

Ахмес стверджує, закріпленні матеріалу, а при подальшому закріпленні

що скопіював текст з оригіналу завдання можуть бути дані в словесній формі. двохсотрічної

Запитання, з якими працюють учні при розв’язуванні

давності. Задача 79 з

папірусу має кросвордів, навчають їх вмінню самим формулювати наступний зміст: В

семи будинках запитання і визначення. Картки, що мають тільки містять по сім запитання, при повторенні навчального матеріалу кішок.

пропонуються більш сильним учням, а слабші учні в цей же час розв’язують ті ж самі кросворди в зоровій формі з опорою на наочність.

Потрібно слідкувати за тим, як виконується завдання, і якщо зустрічаються помилки дати картку з готовими відповідями, щоб учень міг бачити і правильну відповідь, і правильне написання слів. При фронтальній роботі з класом сітка кросворда креслиться на дошці, і учні по черзі виходять до дошки та вписують потрібні терміни в клітинки кросворду.

Окрім традиційних на уроках можливе використання ще й угорських кросвордів. Складаючи їх, можна не лише перевірити знання учнями теоретичного матеріалу, а й активізувати пізнавальні здібності учнів, розвивати їх увагу, пам'ять, мислення.

Всі ми знаємо, що увага – це зосередженість і направленість психічної діяльності на певний об’єкт. Саме угорські кросворди дають змогу розвивати такі властивості уваги як:

Ø об’єм (кількість об’єктів, які можуть бути сприйняті і збережені людиною у відносно короткий проміжок часу);

Ø розподіл ( здатність одночасно утримувати у свідомості об’єкти різної діяльності);

Ø переключення ( можливість швидкого переходу уваги з одного об’єкту на інший).

Кожна кішка ловить по сім мишей в день, а кожна миша, залишся б вона живою, з'їла б за той же день сім колосів пшениці. Якщо кожний колос може дати сім гекатів зерна, скільки всього тут перераховано?

Математика формувалася нерівномірно, в різний час в її розвиток внесли свій внесок Вавілон, Стародавня Греція,

Китай, Індія. До речі, математика у Вавілоні мала справу не тільки з арифметикою, але і з алгеброю, серйозно випереджуючи в цьому відношенні Єгипет. Давньогрецький математик Діофант майже

через дві тисячі літ після появи папірусу Хінда запропонував таку задачу: "Знайти три числа, які при попарному складанні дають в

сумі двадцять,

тридцять і сорок".

Але не можна забувати і про процеси пам’яті, які розвиваються при роботі над кросвордами:

Ø запам’ятовування;

Ø збереження;

Ø відтворення ( впізнання, спогад, власне пригадування).

Не можна також не відмітити, що включення в навчальний процес кросвордів може бути стимулом, адже вони добре активізують пізнавальну діяльність учнів.

Запропоновані кросворди розраховані на учнів різних рівнів знань. Їх можна використовувати під час актуалізації опорних знань учнів (інтерактивна технологія «Мікрофон», метод «Незакінчені речення», математичні диктанти); узагальнення та систематизації знань учнів (колективна, індивідуальна, диференційована робота учнів); підсумок уроку.

Крім того, розгадування кросвордів – цікава форма проведення вільного часу. За їх допомогою ви зможете розкрити в собі невідомі раніше таланти і підвищити впевненість у своїх можливостях. Відомо, що ні для кого не секрет, що така впевненість і лежить в основі життєвого успіху.

Поради щодо використання угорських кросвордів:

Ø Відшукати в кросворді математичний термін (закреслити його) Ø Можливі завдання учням:

- дати означення даного терміну;

- вказати, де він використовується в практичній діяльності; - пригадати, де з ним зустрічалися ( крім уроків математики); - запитати в товариша (оцінити його).

Розглянемо, як використовуються кросворди (традиційні та угорські) для активізації запам’ятовування математичних термінів при вивченні окремих тем на уроках.

Складання кросвордів учнями – це досить корисний вид самостійної роботи, що дає школяру можливість самореалізації.

Кросворд (ребус, чайнворд тощо) – зручна форма активізації пізнавальної діяльності учнів, їхнього мислення. В процесі підготовки кросворду учню необхідно ретельно опрацювати теоретичний і практичний матеріал, звернутись не лише до лекційних матеріалів і підручників, а й до додаткової та довідкової літератури. В ході такого опрацювання і відбору матеріалу учень, без сумніву, глибше засвоює додаткову інформацію, яка поступово накопичується, формуючи більш високий рівень знань. У той самий час нестандартна форма завдання стимулює нестандартний підхід до його виконання, отже, активізується не тільки пізнавальна діяльність, а й творче начало майбутніх фахівців.

З методичної точки зору особливо доцільне складання тематичних кросвордів. Це вимагає грунтовних знань з вибраної теми, уміння чітко формулювати визначення понять. Тематичні кросворди можна використати як для фронтальної, так і для індивідуальної роботи з учнями.

Коли лише починається вивчення математичних тем у школі, доцільно використовувати переважно готові кросворди. Їх може складати й учитель. Як тільки учні відчують привабливість такої діяльності, настає час пропонувти їм самим складати кросворди. Цим можна займатися як вдома, так і на уроках. Складають кросворди учні або індивідуально, або в групі. Рекомендовано використовувати такі завдання на складання кросвордів: дається набір термінів і слів із конкретної теми, необхідно створити сітку з відповідних за горизонталлю і вертикаллю слів, пронумерувати, відібрати і скласти питання до них; називається лише тема курсу технологій, все інше учні роблять самі.

Необхідно пам’ятати, що найбільшу увагу в процесі виконання такої роботи слід приділяти формулюванню питань. Проблема постановки питання – це проблема розвитку високоякісного мислення. Гарне питання допомагає абсолютно інакше бачити суть вивченого і шукати відповідь шляхами, про які раніше ніхто і не думав. А головне – воно свідчить про розуміння навчального матеріалу.

Відзначимо, що складені учнями кросворди мають «працювати». Їх можна пропонувати однокласникам або учням паралельного класу. Необхідно повідомляти авторів про громадську користь їхньої праці. Це приносить їм задоволення і слугує додатковим моральним стимулом.

Слід високо оцінювати успіхи школярів і обов’язково заохочувати, особливо в процесі складання «правильних» симетричних кросвордів.

Завдання створення кросвордів можна розв’язувати одним із програмних засобів: Microsoft Word, Microsoft Excel, Microsoft PowerPoint.

Основні прийоми створення кросворду в Microsoft Word: створення сітки графічним методом у процесі цього (всі елементи мають бути згруповані) створення сітки табличним методом (у процесі цього межі непотрібних осередків стираються) номери або вставляють безпосередньо в осередки, або записують поряд з відповідними осередками; завдання до кросворду можуть бути розташовані звичайним способом або оформлені у вигляді виносок до відповідних клітин.

Вимоги до створення кросворду в Microsoft Word: наявність сітки; наявність нумерації; наявність грамотно сформульованих завдань до кросворду; наочне оформлення і розташування кросворду на сторінці.

Переваги методу: можливість багатократного друкування; незалежність від комп’ютера в процесі використання; простота реалізації.

Недоліки методу: неефективна можливість використання в електронному вигляді; неможливість автоматизації перевірки результату; створюється в основному лише для роботи на папері.

Основні прийоми створення кросворду в Microsoft PowerPoint: створення сітки табличним методом; у процесі цього межі непотрібних осередків стираються; номери або вставляють безпосередньо в осередки, або записують поряд з відповідними осередками; завдання до кросворду можуть бути розташовані звичайним способом або на кожне питання відводиться окремий слайд; розв’язання кросворду має бути організоване автоматично, з використанням гіперпосилань.

Вимоги до створення кросворду в Microsoft PowerPoint: наявність сітки; наявність нумерації; наявність грамотно сформульованих завдань до кросворду; наочне оформлення і розташування кросворду на слайді; наявність можливості вибору правильної відповіді і присутність неправильних відповідей з гіперпосиланнями на автоматичну появу правильної відповіді в сітці і перехід на слайд неправильно в процесі вибору неправильної відповіді.

Переваги методу: можливість багатократного використання; ефективна можливість використання в електронному вигляді; можливість використання в навчальних цілях.

Недоліки методу: неможливість друкування; залежність від комп’ютера; трудність в реалізації; перевірка результату відбувається в процесі вибору відповідей до тих пір, поки учень не впорається із завданням.

Основні прийоми створення кросворду в Microsoft Excel: сітка кросворду створюється шляхом позначення меж осередків і налаштування їх ширини і висоти так, щоб вони вийшли квадратними; завдання до кросворду можуть бути розташовані звичайним способом або оформлені у вигляді приміток до осередків, в яких знаходиться нумерація; перевірка правильності розгадування кросворду може бути здійснена за допомогою умовного форматування (наприклад, якщо в осередок введена правильна літера, то осередок заливається певним кольором або йде підрахунок правильних літер у словах).

Вимоги до створення кросворду в Microsoft Excel: наявність сітки; наявність нумерації; наявність грамотного сформульованих завдань до кросворду; наочне оформлення і розташування кросворду на робочому аркуші; наявність перевірки правильності розв’язання кросворду.

Переваги методу: можливість багатократного друкування; можливість розміщення великого за розмірами кросворду; можливість автоматизації перевірки результату; створюється кросворд не лише для роботи на папері, а й в електронному вигляді; ефективна можливість використання в електронному вигляді.

Недоліки методу: залежність від комп’ютера в процесі використання; налаштування перевірки вимагає певних знань.

Практика показала, що найбільш легким в оволодінні є спосіб створення кросворду в Microsoft Word. Саме він найчастіше використовується учнями. Досить складним в освоєнні є спосіб створення в Microsoft Excel. Кожний із способів вимагає чималої кількості часу. Всі перераховані способи мають як низку переваг, так і низку недоліків.

В мети дичці наведені приклади кросвордів, створеного в Microsoft Word для 5 – 11 класів з таких тем: «Рівняння» [14], «Натуральны числа»

[14], «Дробові чила»[14], «Відношення і пропорції» [9], «Подільність чисел» [4], «Рівняння» [16], «Функція» [8], «Цілі вирази» [19], «Найпростіші геометричні фігури та їх властивості» [11], «Трикутники» [20], «Коло і круг. Геометричні побудови» [18], «Чотирикутники» [16], «Розв׳язування прямокутних трикутників» [18], «Розвязування трикутників» [11], «Початкові відомості із стереометрії» [11], «Елементи прикладної математики» [15], «Квадратична функція» [20], «Тригонометричні функції» [16], «Многогранники» [2, 5], «Тіла обертання» [6, 7], «Площі поверхонь геометричних тіл» [5].

Математика в кросвордах

Математика 5 клас

1. Значення змінної, яке перетворює рівняння в правильну рівність (корінь);

2. Кількість нулів у числі 10 000 000 (сім);

3. Дія першого ступеня (додавання);

4. Тисяча кілограмів (тонна);

5. Дія другого ступеня (ділення);

6. Число, яке не впливає на результат під час множення (один);

7. Шкільне приладдя, за допомогою якого будують відрізки, прямі та промені (лінійка);

8. Найбільше одноцифрове число (дев’ять).

Ключове слово – рівняння.

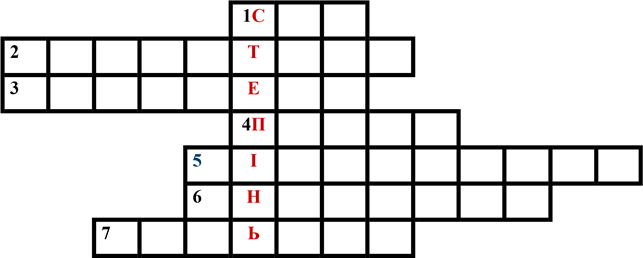
1. Найменше трицифрове число (сто);

2. Замкнена ламана з трьох ланок (трикутник);

3. Сума довжин усіх сторін многокутника (периметр);

4. Добуток ширини на довжину (площа);

5. Дія першого ступеня (віднімання);

6. Дія другого ступеня (множення);

7. Компонент дії ділення (дільник).

Ключове слово – степінь.

1. Корінь рівняння 3х = 12. (чотири)

2. а² = 9; а = ? (три)

3. Периметр прямокутника дорівнює 20 см, одна його сторона – 3 см.

Знайдіть другу сторону. (сім)

4. Знайти сторону квадрата, площа якого дорівнює 100 см². (десять)

5. Одиниця вимірювання об’єму. (літр)

6. Число, яке не є натуральним. (нуль)

7. 4² = ? (шістнадцять)

8. Число, яке не впливає на результат під час множення. (один)

9. Прямокутний паралелепіпед, у якого всі вимірі рівні. (куб)

Ключове слово – чисельник.

Математика – найкоротший шлях до самостійного мислення.

В. Каверін

1. Кут, градусна міра якого дорівнює 180º. (розгорнутий)

2. Половина від 26. ( тринадцять)

3. Одиниця вимірювання кутів. (градус)

4. Корінь рівняння 3х – х + 5 = 21. (вісім)

5. Периметр прямокутника дорівнює 28 см. Одна його сторона дорівнює 5 см.

Знайдіть другу сторону прямокутника. (дев’ять)

6. Тисяча кілограмів. (тонна)

7. 15х = 0, х = ? (нуль)

8. 1²ºº³ = ? (один)

9. Прямокутник, у якого всі сторони рівні. (квадрат)

Ключове слово – знаменник.

Закресліть по горизонталі та вертикалі математичні терміни, а з букв, що залишилися, складіть слово, яке дасть назву числам, що використовуються під час лічби предметів (літери можуть повторюватись)

З	М	Е	Н	Ш	У	В	А	Н	Е
Д	Н	У	М	Е	Р	А	Ц	І	А
О	Ц	И	Ф	Р	А	С	У	М	Я
Д	Н	А	+	В	=	В	+	А	О
А	У	А	Л	М	М	L	А	Т	Д
Н	Р	Н	Ь	І	Н	У	Л	Ь	И
К	В	І	Д'	Є	М	Н	И	К	Н
И	П	О	Р	І	В	Н	Я	Т	И

Відповідь: натуральні числа.

Закресліть по горизонталі та вертикалі математичні терміни, а з букв, що залишилися, складіть слова, які дають узагальнення цим математичним термінам ( літери можуть повторюватись)

Відповідь: дії з числами

Розвиток мислення

Задумайте число (менше 10, крім 0) Помножте його на 3.

До результату додайте 2.

Одержане число помножте на 3.

До результату додайте задумане число.

Першу цифру відповіді закресліть.

До отриманого додайте 2.

Одержане поділіть на 4.

До результату додайте 19.

5 клас

що залишилися, складіть слово, яке дає узагальнення цим математичним термінам ( літери можуть повторюватись)

Відповідь: це многокутники.

5 клас

що залишилися складіть назву теми, яку ми вивчаємо ( літери можуть повторюватись)

Відповідь :дробові числа

Розвиток мислення

Задумате число менше 10 (крім 0)

Помножте на 5.

Результат подвоїти.

До результату додайте 14.

Від суми відніміть 8.

Першу цифру закресліть.

Результат поділіть на 3.

До частки додайте 10.

5 клас

що залишилися складіть назву теми, яку ми вивчаємо ( літери можуть повторюватись)

Відповідь: десяткові дроби, дії над ними.

Жартівливі приклади часто мають більше значення, ніж корисні.

М. Штіфель

1. Як називають числа 1, 3, 5, 7, 9… (непарні);

2. Число, яке має тільки два дільники (просте);

3. Число, яке має більше, ніж два дільники (складене);

4. Дія другого ступеня (ділення);

5. Одиниця вимірювання об’єму (літр);

6. Число, на яке не можна ділити (нуль);

7. Добуток кількох однакових множників (степінь);

8. Рівність, що містить невідоме (рівняння);

9. Дільник, який є у декількох різних чисел (спільний);

10. Друге за порядком розташування, просте число (три);

11. Значення змінної, яке перетворює рівняння в правильну рівність (корінь).

Ключове слово – подільність.

1. 7,5 · 2 + 35 = ? (п’ятдесят);

2. ( )² · 250 = ? (сорок);

3. Частка двох чисел (відношення);

4. 2 – це найменше … число (просте);

5. Добуток крайніх членів пропорції дорівнює добутку середніх її членів

– це … властивість пропорції (основна);

6. Корінь рівняння ( х + 4 ) · 5 = 25 (три);

7. 50% від 40 (двадцять);

8. 64 · = ? (вісім); 9. Обчислити: 2¹ · 1² + 2¹ · ¹ = ? (п’ять).

2 3 2 3

Ключове слово – пропорція.

1. Вони бувають лінійні, стовпчасті та секторні (діаграми);

2. + , - , < , > (знаки);

3. Відрізок, що сполучає дві точки на колі і проходить через його центр

(діаметр);

4. наближене число, що дорівнює відношенню довжини кола до його діаметра (Пі);

5. Частина площини, що обмежена колом (круг);

6. Частина круга, обмежена двома радіусами та дугою (сектор).

Ключове слово – радіус.

Розвиток мислення

(Відгадаю число)

Задумане число помножте на 6.

Від результату відняти 5.

Різницю збільшити у 3 рази.

До результату додати 1.

Розділити число на половину.

До даного числа додати 1.

Суму поділити на половину.

Додати 7.

(щоб вгадати задумане число потрібно результат поділити на 9)

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися, складіть назву дії , яка допомагає дізнатися в скільки разів одне число більше від другого (букви можуть повторюватися )

Відповідь: ділення чисел

Розвиток мислення

Задумайте число менше 10 (не 0).

Додайте до нього 29.

Останню цифру суми закресліть.

Результат помножте на 10.

До добутку додайте 4.

Одержане помножте на 3.

Від результату відніміть 2.

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися складіть слово, яке вказує на те , що число можна поділити на інше

( літери можна використовувати не один раз)

О	П	О	К	А	З	Н	И	К	Н	С	К
С	К	В	А	Д	Р	А	Т	К	У	Б	Н
Н	Д	І	Л	Ь	Н	И	К	О	Н	Д	С
О	Н	Е	П	А	Р	Н	Е	Ь	С	Т	Д
В	П	А	Р	Н	Е	К	Р	А	Т	Н	Е
А	С	Т	Е	П	І	Н	Ь	Л	І	І	П

Відповідь: подільність

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися складіть назву чисел, які раніше називали “ламаними числами” ( літери можуть повторюватись)

Відповідь: дробові числа.

Розвиток мислення

(Відгадай день народження)

Запросити бажаючого і запропонувати йому помножити дату свого народження на 2.

До цього числа додати 5.

Суму помножити на 50.

До результату додати номер місяця свого дня народження.

Вголос назвати результат.

(щоб назвати число і місяць дня народження потрібно від результату відняти 250. В результаті повино вийти трохзначне або чотиризначне числа. Перша і друга цифри вказують на число дня народження, третя і четверта – на місяць. )

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися складіть назву теми, в якій зустрічаються ці терміни (літери можуть повторюватися)

Відповідь: коло та круг

Розвиток мислення

(Відгадаю число)

Задумай число.

Додай до нього 3.

Суму помножте на 6.

Від результату відняти 3.

Відняти задумане число.

Поділити на 5.

(Щоб взнати задумане число потрібно від результату відняти 3)

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися складіть слово, без якого не може існувати ні відношення ні пропорція ( літери можуть повторюватися)

С	В	І	Д	Н	О	Ш	Е	Н	Н	Я
Е	П	Р	О	П	О	Р	Ц	І	Я	К
Р	Р	І	В	Н	І	С	Т	Ь	А	Р
Е	Ч	Д	І	А	Г	Р	А	М	А	А
Д	К	Л	І	Н	І	Й	Н	А	С	Й
Н	Т	С	Е	К	Т	О	Р	Н	А	Н
І	С	Т	О	П	Ч	А	С	Т	А	І
В	Л	А	С	Т	И	В	І	С	Т	Ь

Відповідь: частка

Розвиток мислення

Задумайте число менше 10 (крім 0).

Помножте на 25. Додайте 3.

Суму помножте на 4.

Закресліть першу цифру добутку. Піднесіть до квадрату. Цифри результату додайте.

Додайте 7.

Угорський кросворд

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися складіть слова, які дадуть узагальнення всім термінам, що тут зустрічалися ( літери можуть повторюватися)

Відповідь: геометричні фігури.

1. Другий степінь числа (квадрат);

2. Значення змінної, яке перетворює рівняння в правильну рівність

(корінь);

3. Дія першого ступеня (додавання);

4. Невідоме число в рівнянні (змінна);

5. Як ще називають корінь рівняння? (розв’язок);

6. Рівняння виду ах = в (лінійне);

7. Два рівняння, що мають однакові розв’язки (рівносильні);

8. Корінь рівняння 3х = 27 (дев'ять).

Ключове слово – рівняння.

1. Як називають число під рискою дробу? (знаменник);

2. Замість «?» вказати необхідний показник х⁶ : (х · х⁵) = х^? (нуль);

3. (х³ · х⁷) : х⁹ = х^? (один);

4. Кут, градусна міра якого менша ніж 90⁰ (гострий);

5. (а¹⁰)² · (а⁵)⁴ = а^? (сорок);

6. х¹⁰: (х¹⁰ : х⁴) = х^? (чотири);

7. Компонент дії ділення (ділене);

8. (а⁶ : а³)³ = а^? (дев’ять);

9. (х¹¹)²: (х³)³= х^? (тринадцять).

Ключове слово – многочлен.

1. Буквена рівність або вираз (формула);

2. Незалежна змінна функції (аргумент);

3. Спосіб задання функції у вигляді таблиці (табличний);

4. Якою літерою позначають вісь абсцис? (ікс);

5. Рівність двох відношень (пропорція);

6. Множина всіх точок координатної площини (графік);

7. Графік лінійної функції (пряма).

Ключове слово – функція.

Найвище призначення математики полягає в тому, щоб знаходити прихований порядок у хаосі, що оточує нас.

Н. Вінер

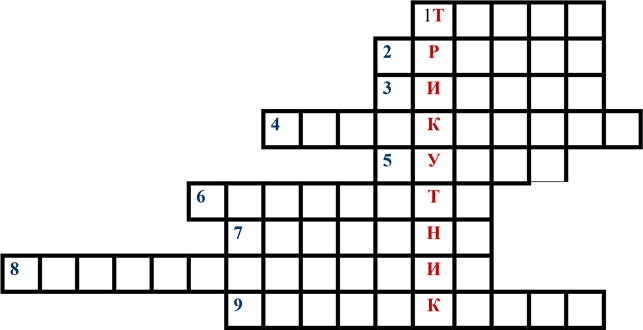
1. Найпростіша геометрична фігура (точка);

2. Одиниця вимірювання кутів (градус);

3. Перпендикуляр, опущений з вершини трикутника на пряму, на якій лежить його протилежна сторона (висота);

4. Відрізок, що ділить кут трикутника на дві рівні частини (бісектриса);

5. Кут, градусна міра якого більша ніж 90º і менша ніж 180º (тупий);

6. Сума довжин усіх сторін трикутника (периметр);

7. Відрізок, що сполучає вершину трикутника із серединою протилежної сторони (медіана);

8. Трикутник, у якого дві сторони рівні (рівнобедрений);

9. Трикутник, кут якого дорівнює 90º (прямокутний).

Ключове слово – трикутник.

1. Вона ідеально рівна і нескінченна в обидва боки (пряма);

2. Фігура, що складається з усіх точок площини, рівновіддалених від даної точки (коло);

3. Паралелограм з рівними сторонами (ромб);

4. Частина площини, обмежена колом (круг);

5. Відрізок, що сполучає дві довільні точки на колі (хорда);

6. Пряма, що має з колом одну спільну точку (дотична); 7. Шкільне приладдя для виконання малюнків на уроках (олівець);

8. Відрізок, що сполучає центр кола з точкою на колі (радіус).

Ключове слово – побудова.

Математика – найкоротший шлях до самостійного мислення.

В. Каверін

1. Кут, менший 90º (гострий);

2. Яке твердження доводиться? (теорема);

3. Перпендикуляр, опущений з вершини кута на протилежну сторону

(висота);

4. Два промені, що виходять з однієї точки (кут);

5. В яких одиницях вимірюють кути (градус);

6. Кут, більший за 90º і менший за 180º (тупий);

7. Кут, що дорівнює 90º (прямий);

8. Кути, у яких сторони є доповняльними променями (вертикальні);

9. Промінь, що ділить кут навпіл (бісектриса).

Ключове слово – трикутник.

Угорський кросворд

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися, складіть назву науки, яка вивчає геометричні фігури на площині ( літери можуть повторюватися)

Відповідь: планіметрія.

Розвиток мислення

Задумайте двоцифрове число.

Додайте 7.

Суму відніміть від 110.

До різниці додайте 15.

До результату додайте задумане число.

Суму поділіть на половину.

Від частки відніміть 9.

Результат помножте на 3.

Угорський кросворд

Закресліть по горизонталі та вертикалі математичні терміни, а з літер, що залишилися, складіть слова, що є елементами многокутників ( літери можуть повторюватися)

Відповідь: сторони, вершини.

Розвиток мислення

Задумайте число менше 100.

Додайте 12.

Суму відніміть від 130.

До різниці додайте 5.

До різниці додайте задумане число.

Від суми відніміть 120.

Результат помножте на 7.

Відніміть 1.

Різницю розділіть на половину. Додайте 30.

1.Один із видів перетворення подібності (гомотетія);

2. Відрізок, що з’єднує вершину трикутника із серединою протилежної сторони (медіана);

3. Знайти довжину гіпотенузи прямокутного трикутника, якщо його катети дорівнюють 12 см і 9 см (п'ятнадцять);

4. Вчений, чия теорема мала назву «магістр математики» (Піфагор);

5. Твердження, що потребує доведення (теорема);

6. Чому дорівнює значення виразу sin² 71^о + cos² 71^о (один);

7. Знайти невідому сторону прямокутника, діагональ якого дорівнює 10 см, а одна із сторін – 6 см (вісім).

Ключове слово – тангенс.

1. Назва прямокутного трикутника зі сторонами 3, 4, 5. (єгипетський)

2. Сторона прямокутного трикутника, яка лежить напроти прямого кута.

(гіпотенуза)

3. Ім’я, яке прийняла мати Піфагора після того, як збулося пророцтво оракула. (Піфіада)

4. Острів, на якому народився цей математик. (Самос)

5. Країна, в якій жив Піфагор. (Греція)

6. Місто, в якому цей математик пробув 12 років у полоні. (Вавилон)

7. Ім’я першого вчителя Піфагора який навчав його основам музики та живопису. (Гермодамас)

Ключове слово – Піфагор.

Угорський кросворд

Відшукайте по горизонталі та вертикалі математичні терміни, а з решти літер складіть слово , що узагальнить даний математичний матеріал ( літери можуть повторюватися).

Відповідь: читирикутники

Розвиток мислення

Задумайте будь-яке число (крім 0).

Подвоїти його.

До результату додайте 1.

Результат помножте на 5.

Відкиньте всі цифри, крім останньої.

Помножте число на себе.

Додайте цифри результату.

Угорський кросворд

По вертикалі та горизонталі відшукайте знайомі терміни, дайте їх означення, а з букв, що залишилися складіть назву теореми, яка дозволяє знаходити невідомі сторони прямокутних трикутників (літери можуть повторюватися)

Відповідь: теорема Піфагора

Розвиток мислення

(Відгадаю число)

Задумайте число.

Помножте на 4.

Відніміть 3.

Різницю помножиьи на 3.

Добуток збільшіть на 15.

Результат поділіть на 4.

Додайте 1.

(Щоб взнати задумане число, потрібно одержаний результат поділити на 3)

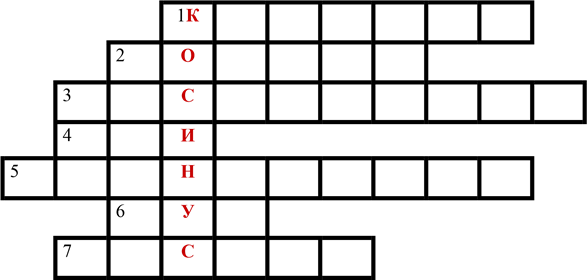
1. Прямокутник, діагоналі якого перетинаються під кутом 90^о (квадрат);

2. Абсолютна величина вектора (модуль);

3. Промінь, що виходить із вершини кута, проходить між його сторонами і ділить кут навпіл (бісектриса);

4. Знайти довжину катета прямокутного трикутника, якщо гіпотенуза дорівнює 5 см, а інший катет – 4 см (три);

5. Знайдіть модуль вектора, координати якого дорівнюють (12; 9)

(п'ятнадцять);

6. Фігура, що складається з двох променів, які виходять з однієї точки (кут); 7. Відрізок, що проведений із вершини трикутника перпендикулярно до протилежної сторони висота).

Ключове слово – косинус.

1. Радіус основи циліндра дорівнює 2 см, висота – 5 см. Знайти площу бічної поверхні циліндра. S = ? π см² (двадцять);

2. Об’єм циліндра дорівнює 27 π см², радіус основи – 3 см. Знайти його висоту (три);

3. Проекція кола під час паралельного проектування (еліпс);

4. Відрізок, що сполучає точки кіл кругів – основ циліндра (твірна);

5. Осьовий переріз циліндра – квадрат зі стороною 4 см. Знайти об’єм циліндра. V = ? π см³ (шістнадцять);

6. Об’єм циліндра дорівнює 40 π см³, висота – 10 см. Знайти радіус основи циліндра (два);

7. Яку з геометричних фігур можна обертати навколо однієї із своїх сторін, щоб утворився циліндр? (прямокутник).

Ключове слово – циліндр.

1.Переріз конуса площиною, паралельною до основи конуса (круг);

2. Висота конуса дорівнює 4,8 см, радіус основи – 5 см. Знайти його об’єм. V = ? (сорок);

3. Радіус основи конуса дорівнює 2 см, твірна – 8 см. Знайти площу бічної поверхні конуса. (шістнадцять);

4. Яку із геометричних фігур треба обертати, щоб утворився конус? (трикутник);

5. Чому дорівнює площа осьового перерізу конуса, твірна якого дорівнює

42 см, а кут при вершині осьового перерізу дорівнює 30^о? (вісім).

			1К
		2	О
3			Н
4			У
	5		С

Ключове слово – конус.

1. Сторона правильної трикутної піраміди дорівнює 4 см, апофема - 8 см.

Знайти площу бічної поверхні піраміди (п’ятдесят);

2. Сторона основи правильної чотирикутної піраміди дорівнює 4 см, висота –

3 см. Знайти об’єм піраміди (шістнадцять);

3. Відрізок, що з’єднує вершину піраміди із вершиною її основи (ребро);

4. Сторона основи правильної чотирикутної піраміди дорівнює 2 см, апофема

– 4 см. Знайти площу повної поверхні піраміди (двадцять);

5. Висота бічної грані правильної піраміди, що проведена з її вершини

(апофема);

6. Основою піраміди є ромб з діагоналями 8 і 9 см, Об’єм піраміди дорівнює 84 см³. Знайти висоту піраміди (сім);

7. Основою піраміди є прямокутний трикутник із гіпотенузою 8 см і катетом

6 см. Висота піраміди дорівнює √7 см. Знайти об’єм піраміди (чотирнадцять);

8. Переріз правильної чотирикутної піраміди, що паралельний до її основи (квадрат).

Ключове слово – піраміда.

Алгебра 9 клас

1. Вчений, який у 1657 році видав перший трактат із теорії ймовірностей (Гюйгенс);

2. Якщо дві події не можуть відбутися разом вони називаються …

(несумісні);

3. Подія, яка внаслідок даного випробування обов’язково має відбутися (вірогідна);

4. Задумано двозначне число. Знайти ймовірність того, що задуманим числом виявиться випадково назване двоцифрове число. Записати здобуте число у

1 знаменнику дробу (дев’яносто);

5. На п’яти однакових картках написано букви А, Е, Н, П, Р. Яка ймовірність того, що випадковим чином розкладені в ряд три картки дадуть слово

«НЕП»? Записати здобуте число у знаменнику дробу (шістдесят);

6. Ймовірність того, що стрілець під час деякого пострілу виб’є 10 очок, дорівнює 0,1, 9очок – 0,3, 8 або менше очок – 0,6. Знайти ймовірність того, що стрілець за одного пострілу виб’є не менше ніж 9 очок. У відповідь записати цифру, що стоїть у розряді десятих здобутого числа (чотири);

7. Кинуто дві гральні кісточки. Яка ймовірність того, що сума очок, що випаде, не менша від 8? У відповідь записати знаменник здобутого дробу (дванадцять);

8. Квиток на футбольний матч Романенко може купити з імовірністю 0,3, на баскетбольний турнір – з імовірністю 0,4, а на волейбольний матч – з імовірністю 0,2. Яка ймовірність потрапити на змагання, де грають ногами, якщо купується один квиток? У відповідь записати цифру, що стоїть у розряді десятих здобутого числа (шість);

9. Микола купив три різні акції. Ймовірність зростання в ціні першої акції дорівнює , другої – , а третьої – . Знайти ймовірність того, що всі акції зростуть у ціні. У відповідь записати знаменник здобутого дробу (сорок); 10. У ящику 10 деталей, серед яких 6 пофарбованих. Навмання вибирається 4 деталі. Знайти ймовірність того, що всі витягнуті деталі виявляться пофарбованими. У відповідь записати знаменник здобутого дробу (чотирнадцять);

11. У цеху працює 6 чоловіків і 4 жінки. За табельними номерами вибрано 7 осіб. Знайти ймовірність того, що серед вибраних осіб виявиться 3 жінки. У відповідь записати цифру, що стоїть у розряді десятих здобутого числа (п’ять).

Ключове слово – ймовірність.

Геометрія 9 клас

1. Многогранник, який складається з плоского многокутника, точки, яка не лежить у площині основи, і всіх відрізків, що сполучають цю точку з точками основи (піраміда);

2. Якими є основи призми? (рівні);

3. З яких геометричних фігур складається бічна поверхня призми?

(паралелограм);

4. Яку назву мають півплощини, що утворюють двогранний кут? (грані);

5. Висота бічної грані правильної піраміди, що проведена з її вершини

(апофема);

6. Тіло, поверхня якого складається зі скінченної кількості плоских многокутників (многогранник);

7. Пряма, що обмежує грані двогранного кута (ребро);

8. Призма, основою якої є паралелограм (паралелепіпед);

9. Які між собою площини, в яких лежать протилежні грані паралелепіпеда?

(паралельні);

10. Кут, утворений двома півплощинами і прямою, що їх обмежує

(двогранний);

11. Многогранник, що складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням всіх відрізків, що сполучають відповідні точки цих многокутників (призма);

12. Прямокутний паралелепіпед, у якого всі ребра рівні (куб);

13. Бічне ребро правильної чотирикутної призми – це її… (висота).

Ключове слово – многогранник

Угорські кросворди на уроках геометрії в 7 класі

Тема «Найпростіші геометричні фігури та їх властивості»

Г	Е	О	О	И	Н	Ь	Т	Я
Т	О	М	Д	Й	Ч	Т	Р	І
К	Ч	Е	И	Н	И	И	И	Р
А	П	Т	Р	І	Я	Ж	Е	Т
О	Р	Р	І	З	О	А	Л	Е
М	І	Д	М	А	К	Н	А	М
І	В	Р	Я	О	Щ	И	Н	І
Н	Ь	П	П	Л	П	Л	А	Н

1. Як називають науку про властивості геометричних фігури? (геометрія)

2. Яка фігура є найпростішою? (точка)

3. Про яку геометричну фігуру дає уявлення поверхня стола? (площина)

4. Як називають частину геометрії, що вивчає фігури на площині?(планіметрія)

5. Як читають знак ϵ? (належить)

6. Як називають відрізок, який беремо за одиницю вимірювання?

(одиничний)

7. Знайди назви зображених фігур:

. . .

(пряма, відрізок, промінь)

8. Скільки відрізків зображено на р рисунку?

. . .

(три)

«Формули »

К	К	В	А	Н	Ь	К	Ш
У	Б	А	Т	Т	Н	И	В
А	Р	Д	С	У	К	Д	И
Т	В	І	Д	К	І	К	О
П	Р	Я	М	О	С	О	Л
К	Р	И	И	К	Т	А	С
Р	Т	К	Н	П	Ь	Ч	А
У	Г	У	Т	Р	И	З	М

Знайдіть назви фігур, величин. Які знаходимо за допомогою зазначених

формул:

1. S = ab. (прямокутник)

2. Р=4а.(квадрат)

3. V=a³.(куб)

4. S=vt. (відстань)

5. V=s:t.(швидкість)

6. S=πr².(круг)

7. C=2 πr.(коло)

8. t=s:v.(час)

9. P=a+b+c.(трикутник)

10. V=S_оснH.(призма)

Розвиток мислення

Задумайте трьох цифрове число.

Дописати з права те саме число.

Одержане число поділіть на 7.

Результат поділіть на задумане число.

Одержане поділити на 11.

Результат подвоїти.

Обчислити суму цифр.

«Кути»

Г	С	У	Н	М	І	Н	І
О	Е	К	Д	А	І	У	Н
С	Т	Р	И	Й	Н	Т	Ь
Т	С	У	М	І	Ж	А	Л
У	В	Е	Р	Т	И	К	А
П	И	Й	И	Н	И	С	А
П	Г	О	Ш	А	Р	Р	О
Р	З	Р	Р	Б	Т	Т	П
Я	О	Н	Е	І	К	И	С
М	Р	У	В	С	Е	Р	Н
И	Й	Т	И	Й	Т	Р	А

1. Як називається кут, градусна міра якого дорівнює 90^ᵒ?(прямий)

2. Як називається кут, менший від прямого?(гострий)

3. Якщо кут більший за прямий, але менший від розгорнутого, то його називають… (тупий)

4. Промінь, який виходить із вершини кута, проходить між його сторонами і ділить його на два різні кути, називають … (бісектриса)

5. Градусна міра цього кута дорівнює 180^ᵒ. (розгорнутий)

6. Cпільний початок сторін кута називають … кута. (вершина)

7. градуса. (мінута)

8. Як називають прилад, за допомогою якого вимірюють кути?

(транспортир)

9. Як називають кути, сума яких дорівнює 180^ᵒ? (суміжні)

10. мінути. (секунда)

11. Якщо сторони одного кута є доповняльними променями сторін другого кута, то такі кути називають… (вертикальні)

«Взаємне розміщення прямих на площині»

П	П	Е	Р	П	Е	Н	Д	И	К
Е	С	О	З	Я	В	И	С	Н	У
Р	І	Т	Н	Н	Е	В	К	О	Л
П	Ч	Е	А	Н	М	О	Л	В	Я
Е	Н	О	Ч	Е	У	В	І	О	Р
Н	А	Р	А	К	С	А	Д	К	Н
Д	І	Е	М	А	І	О	М	А	І
И	Н	Ь	Л	Е	Л	А	Р	А	П
К	У	Л	Я	Р	Н	І	С	Т	Ь

1. Твердження, яке не потрібно доводити.(аксіома)

2. Твердження, яке потрібно доводити.(теорета)

3. Твердження, у якому пояснюється зміст того чи іншого поняття.(означення)

4. Те, що дано.(умова)

5. Те, що необхідно довести. (висновок)

6. Давньогрецький учений, який написав «Начала». (Евклід)

7. Прямі, які перетинаються під прямим кутом.(перпендикулярні)

8. Прямі на площині, які не перетинаються під прямим кутом.(паралельні)

9. Пряма відносно двох прямих, якщо вона перетинає їх у двох точках(січна)

10. Що означає знак ԫ ?(перпендикулярність)

«Трикутник і його елементи»

М	Е	Д	І	С	Е	К	Т
П	Т	І	Б	В	И	С	Р
Р	Р	А	Н	А	Й	О	И
Я	И	У	Т	Н	И	Т	С
М	О	К	О	Б	Е	А	А
Р	І	В	Н	К	Д	Р	Е
Р	Г	І	Н	А	Т	Е	Н
І	І	Ш	В	О	З	Т	И
В	П	Н	І	Й	З	А	Й
Н	О	Т	Е	Н	У	Й	І
О	С	Т	О	Р	О	Н	Н

1. Які трикутники зображені на рисунках?

а) б) в)

(рівносторонній, рівнобедрений, прямокутний)

2. Скільки існує ознак рівності трикутників?(три)

3. Як називають відрізок, що сполучає вершину трикутника із серединою протилежної сторони? (медіана)

4. Промінь, який виходить із вершини кута і ділить його на два рівних кути, - це … (бісектриса)

5. Перпендикуляр, проведений з вершини трикутника до прямої, що містить його протилежну сторону. (висота)

6. Найбільша сторона прямокутного трикутника. (гіпотенуза)

7. Сторона прямокутного трикутника, що лежить навпроти гострого кута.

(катет)

8. Кут, суміжний із внутрішнім кутом трикутника. (зовнішній)

Т	Р	І	В	Н	О	Б	Е	Д
Р	Ц	Е	Н	Т	П	Е	Р	Р
И	К	У	Т	Р	Е	Н	И	Е
О	Е	Н	Н	О	Ц	Т	М	Н
Р	Ц	Т	И	Ї	Н	Р	Е	И
Т	О	Р	К	Д	І	Р	Т	Й

1. Фігура, сума кутів якої дорівнює 180^ᵒ. (трикутник)

2. Трикутник, два кути якого рівні. (рівнобедрений)

3. У будь-якому трикутнику медіани перетинаються в одній точці. Цю точку називають…(центроїд)

4. У будь-якому трикутнику бісектриси перетинаються в одній точці. Цю точку називають…(інцентр)

5. У будь-якому трикутнику висоти перетинаються в одній точці. Цю точку називають…(ортоцентр)

6. Сума всіх сторін трикутника.(периметр)

Розвиток мислення

Задумайте число менше 100. Додайте 20.

Результат відніміть від 170.

Від одержаного відніміть 6.

До різниці додайте задумане число.

В результаті додайте цифри.

Суму помножте на себе.

Відніміть 1.

Результат поділіть на половину. Додайте 8.

Тема «Коло і круг»

К	Р	А	Д	К	О	Н	Ц
О	Л	О	І	О	Т	И	Е
Х	О	Р	У	Д	С	Ч	Н
М	Е	Д	С	Ь	І	Н	Т
А	Т	А	У	Л	Ч	А	Р
І	Р	Р	К	А	Н	А	И
Д	Ц	И	Д	В	І	Н	Ч

1. Геометрична фігура, яка складається з усіх точок площини, рівновіддалених від поданої точки. (коло)

2. Відрізок, що сполучає центр кола з будь-якою точкою кола.(радіус)

3. Відрізок, що сполучає дві точки кола.(хорда)

4. Найбільша хорда.(діаметр)

5. Прилад, за допомогою якого креслять коло. (циркуль)

6. Скільки радіусів містить один діаметр?(два)

7. Пряма, яка має одну спільну точку з колом.(дотична)

8. Якщо два кола мають спільний центр, то іх називають….

(концентричні)

9. Пряма, що має дві спільні точки з колом.(січна)

«Геометричні перетворення, трикутник»

По горизонталі:

1. Число натурального ряду.(одиниця)

2. Кількість гострих кутів у прямокутному трикутнику.(два)

3. Одна із сторін прямокутного трикутника.(катет)

4. Видатний учений-математик.(Піфагор)

5. Одна з тригонометричних функцій.(косинус)

6. Одне з геометричних перетворень.(рух) По вертикалі:

2. Учений-математик.(Декарт)

4. Одне з геометричних перетворень.(поворот)

7. Сума довжин сторін многокутника.(периметр)

8. Одна з тригонометричних функцій.(тангенс)

9. Важливі точки функції. (нулі)

10. Одна з тригонометричних функцій. (синус)

Тема «Квадратний тричлен, многокутник»

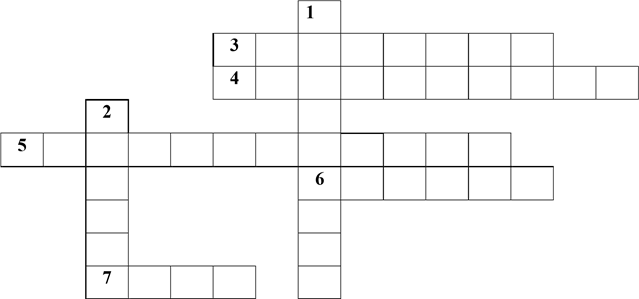
По вертикалі:

1. Спосіб розв’язування рівнянь (графічний)

2. Зображення множини точок, що мають певну властивість.(графік) По горизонталі:

3. Графік функції. (парабола)

4. Назва тричлена.(квадратний)

5. Вид гіперболоїда (тривимірний)

6. Кількість вершин дельтоїда.(чотири)

7. Геометрична фігура. (коло)

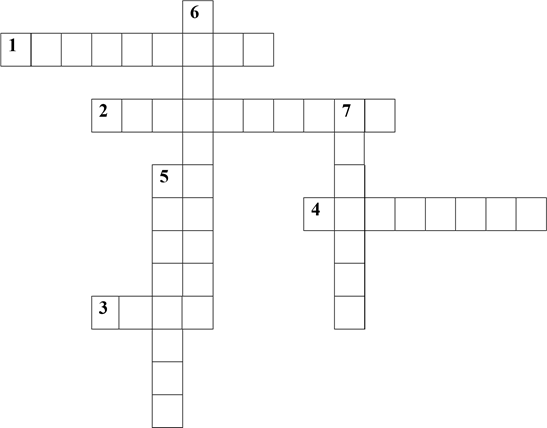
1. Графік функції y=x². (парабола)

2. Множина точок площини, координати яких задовольняють рівність y=f(x). (графік)

𝑥²+ 𝑦²= 16

3. Скільки розв׳язків має система { 𝑦 = 𝑥₂− 5 (чотири)

4. Точка перетину параболи зі своєю віссю. (вершина)

5. Функція, графік якої симетричний відносно осі Oy. (парна) По вертикалі:

4. Напрямок віток параболи y=-x²_.(вниз)

6. Спосіб розв’язування рівнянь або системи рівнянь. (графічний)

7. Яка фігура задається формулою 𝑥

Тема «Елементи прикладної математики»

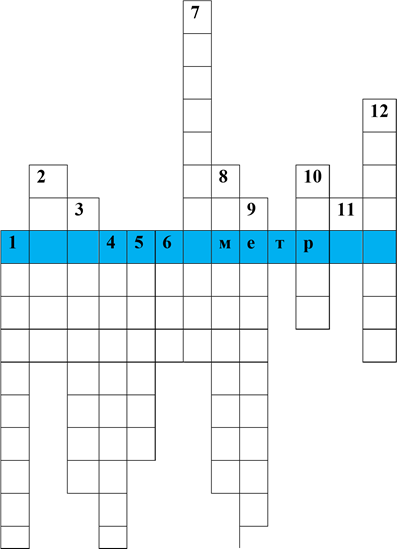
По горизонталі:

1. Вид похибки. (абсолютна)

2. Назва стовпчастої діаграми. (гістограма)

3. Значення вибірки, яке трапляється найчастіше. (мода)

4. Сота частина числа. (відсоток) По вертикалі:

5. Як називають середнє арифметичне усіх значень вибірки. (середнім)

6. Розділ прикладної математики. (статистика)

7. Число, яке «поділяє» навпіл упорядковану сукупність усіх значень вибірки. (медіана)

Люди ніколи не виявляли більшої дотепності, ніж у

вигадуванні гри.

Готфрід Вільгедьм Лейбніц «Тригонометричні функції»

1. sin²𝑥 + cos²𝑥 = 1 – тригонометрична …(тотожність)

2. 2πn, де n є Z, для функції y=sin 𝑥.(період)

3. Графік функції y=sin 𝑥.(синусоїда)

4. …. Коливання.(гармонійні)

5. sin ^𝜋 = …(одиниці) 2

6. cos ^𝜋 = …(нулю) 2

7. Графік функції y=cos х.(косинусоїда)

8. Розташування графіка функції y=cos х відносно осі ординат.(симетрично)

9. Одна з властивостей функції у=tg x.(періодична)

10. Одна з властивостей функції у=cos х (парна)

11. Відношення довжини кола до його діаметра. (пі)

12. Рівність sin х = . (рівняння)

По горизонталі:

1. Геометрична фігура, яка має три вершини.(трикутник)

2. Відстань між площинами основ призми.(висота)

3. Сума всіх сторін многокутника.(периметр)

4. Чотирикутник, у якого протилежні сторони паралельні.(паралелограм)

5. Кількість вершин семикутної призми.(чотирнадцять) По вертикалі:

2. Кінець ребра многогранника.(вершина)

3. Величина, яка вимірюється в квадратних одиницях. (площа)

6. Кількість бічних граней куба.(чотири)

7. Об׳єм куба, сторона основи якого 1 см.(один)

8. Сторона грані многогранника. (ребро)

9. Грань куба. (квадрат)

10. Один з многокутників, що обмежує многогранник. (грань)

По горизонталі:

1. Сума всіх сторін основи піраміди. (периметр)

2. Висота бічної грані піраміди. (апофема)

3. Основа піраміди, у якої всі кути прямі, а сторони рівні. (квадрат)

4. Чому дорівнює об’єм піраміди, площа основи якої – 45 м²,а висота – 6 м? (дев’яносто )

5. Чому дорівнює площа повної поверхні піраміди, якщо площа її основи

– 363 м², а площа бічної поверхні – 137 м²? (п’ятсот) По вертикалі:

6. Бічна грань зрізаної піраміди. (трапеція)

7. Один з многогранників,що обмежує многогранник. (грань)

8. Сторона грані многогранника. (ребро)

9. Одиниця вимірювання довжини. (метр)

10. Величина, яка вимірюється кубічними одиницями. (об’єм)

11. Кількість бічних граней у тетраедра. (три)

12. Кількість вершин у тетраедра. (чотири)

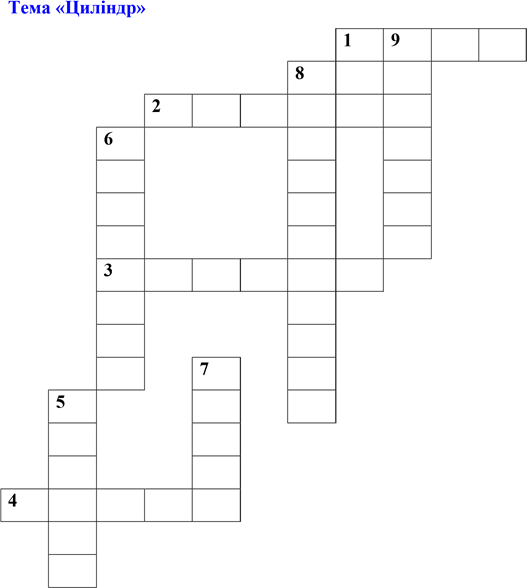
По горизонталі:

1. Чому дорівнює висота циліндра, об’єм якого – 15 см², а площа основи – 15 см²? (один)

2. Відрізок, який сполучає відповідні точки основи циліндра. (твірна)

3. Відстань від точки кола до його центра. (радіус)

4. Відрізок, який сполучає дві точки кола. (хорда) По вертикалі:

5. Відстань між площинами основ циліндра. (висота)

6. «Зовнішня оболонка» просторової фігури. (поверхня)

7. Величина, яка вимірюється квадратними одиницями. (площа)

8. Осьовий переріз прямого циліндра.(прямокутник)

9. Найбільша хорда (діаметр)

По горизонталі:

1. Відстань від точок кола до центру. (радіус)

2. Величина, яку обчислюють за формулою 𝜋𝑅²𝐻, де R – радіус основи,

Н – висота конуса. (об’єм)

3. Осьовим … конуса є рівнобедрений трикутник. (перерізом)

4. Сторона прямокутного трикутника (катет)

5. Відрізок, який з’єднує вершину конуса з точкою його основи. (твірна) По вертикалі:

3. Знайдіть довжину твірної конуса, якщо площа бічної поверхні дорівнює

20π см², а радіус основи – 4 см. (п’ять )

6. Частина круга,обмежена двома радіусами та дугою. (сектор)

7. Величина, яка обчислюється в квадратних одиниця. (площа)

8. Хорда, проведена через центр кола. (діаметр)

9. Пряма, проведена через вершину і центр основи прямого конуса. (вісь)

10. Площина круга конуса. (основа)

11. Властивість, за якою встановлюють рівність трикутників. (ознака)

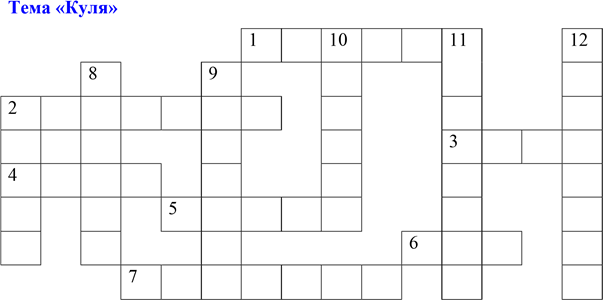
По горизонталі:

1. Відрізок, який сполучає відповідні точки основ многогранників, але відсутні від кулі. (висота)

2. Стереометрія вивчає властивості плоских і неплоских фігур, місце розташування яких - … (простір)

3. Величина, яку можна обчислити за формулою 𝜋𝑅³, де R- радіус кулі.

(об’єм )

4. Кількість центрів симетрії у кулі. (один)

5. Точка, відносно якої всі точки сфери знаходяться на заданій відстані. (центр)

6. Знайдіть радіус сфери, площа якої дорівнює 40 000𝜋 см². (сто) 7. Круг, який утворюється при перетині кулі з площиною. (переріз) По вертикалі:

2. Величина, яку можна обчислити за формулою 4πR², R – радіус кулі.

(площа)

8. Цифра, яка є у запису формул для знаходження площі сфери та об’єму кулі. (чотири)

9. Відрізок, який сполучає дві точки сферичної поверхні і проходить через центр кулі. (діаметр)

10. Частина круга, обмежена двома його радіусами та дугою. (сектор) 11. Порядок виконання дій під час доведення теореми, розв’язування задачі. (алгоритм)

12.Частина круга, обмежена дугою і хордою, що її стягує. (сегмент)

«Площа поверхні геометричних фігур»

		5		6	7
	1

2


			3
4

Запишіть в клітинках рядка чи стовпчика назву або частину назви геометричної фігури,повна поверхня якої обчислюється за вказаною формулою. По горизонталі:

1. 𝑆 = 2𝜋𝑅(𝑅 + 𝐻), де R – радіус основи, Н – висота. (циліндр)

2. S=6a², де а – ребро. (куб)

3. S= 2(ab+bc+ac), де а,b,c – лінійні виміри. (паралелепіпед)

4. S=4𝜋𝑅², R – радіус. (сфера)

По вертикалі:

2. 𝑆 = 𝜋𝑅(𝑅 + 𝐿), де R – радіус основи, L – твірна. (конус)

5. S= S_б+ S_осн, де S_б – площа бічної поверхні, S_осн – площа основи. (піраміда)

6. S= S_б+ 2S_осн, де S_б – площа бічної поверхні, S_осн – площа основи. (призма)

, де а – ребро. (тетраедр)

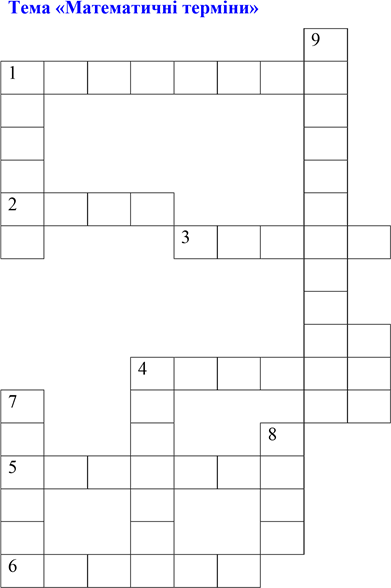
По горизонталі:

1. Просторова геометрична фігура, у якої бічні грані – трикутники. (піраміда)

2. Величина, яка вимірюється в кубічних одиницях. (об’єм)

3. Запис, складений із цифр. (число)

4. Просторова фігура, межа кулі. (сфера)

5. Найбільша хорда кола. (діаметр)

6. Частина круга, обмежена двома його радіусами і дугою. (сектор) По вертикалі:

1. Число π - … для функцій y=tg x і y=сtg x. (період)

4. Частина круга, обмежена дугою і хордою, що її стягує. (сегмент)

7.Відстань від центра кола до будь-якої точки кола. (радіус)

8. Фігура, яка складається з усіх точок площини, що лежать від точки на відстані, не більшій за дану. (круг)

9. Чотирикутник, у якого протилежні сторони паралельні. (паралелограм)

МАТЕМАТИЧНІ РЕБУСИ

Історія математичних ребусів

Серед великої кількості логічних загадок досить розповсюдженими та популярними є математичні (числові) ребуси. Математичний ребус це завдання, в якому шляхом логічних міркувань потрібно розшифрувати значення кожного символу і відновити числовий запис виразу. Якісний ребус повинен мати єдину можливу розшифровку, хоча це правило дотримується не завжди.

Існує кілька різновидів математичного ребусу. Наприклад, в буквених ребусах кожною літерою зашифрована одна певна цифра. При цьому однакові цифри шифруються однією і тією ж літерою, а різним цифрам відповідають різні літери. Математичний буквений ребус називають криптарифмом, якщо в результаті шифрування отримуємо певну осмислену фразу.

У математичних ребусах, зашифрованих іншими значками, наприклад, зірочками , кожен символ може позначати будь-яку цифру від 0 до 9. Причому деякі цифри можуть повторюватися кілька разів, а інші зовсім не використовуватись. Такі ребуси, найчастіше, називають числовими або цифровими. [21]

Класичний приклад математичного буквеного ребусу на додавання належить англійцю Генрі Ернсту Дьюдені (Henry Ernest Dudeney). У 1924 році в червневому номері журналу

"Strand Magazine" (наприкінці XIX століття сер Артур Конан

Дойль писав «Шерлока Холмса» спеціально для цього видання) Дьюдени публікує ребус: SEND + MORE = MONEY . У перекладі з англійської мови ця фраза означає "шліть більше грошей" - лаконічний текст телеграми надісланий чи то студентом до батьків, чи то викрадачами з вимогою викупу.

Єдиним рішенням ребуса Дьюдені є рівність : 9567 +1085 = 10652.

Математичний ребус - досить стара головоломка, винахідник її не відомий. Довгий час авторство помилково приписували американському шахісту Семюелю Лойду (Samuel Loyd). Однак англійський математик Девід Сінгмастер (David Singmaster) у своїй хронології математичних головоломок

"Sources in recreational mathematics" (1993 рік), посилаючись на Віла Шортца

(Will Shortz ), вказує на замітку "Multiplication problem where the letters for 1 - 0 spell Palmerston" в грудневому номері журналу " The American Agriculturist"

за 1864 як перший друкований математичний ребус.

Математичний ребус українською ще називають арифметичним, числовим або цифровим. В англійській мові також використовується кілька назв для позначення даного виду головоломок: Verbal arithmetic, Alphametics, Cryptarithmetic (Crypt - arithmetic), Cryptarithm.

Термін "crypt - arithmetic" належить бельгійському композитору, автору багатьох головоломок Симону

Ватрікванту (Simon Vatriquant), який під псевдонімом "Minos" з 1931 року і до початку Другої світової війни публікував математичні ребуси в бельгійському математичному журналі "Sphinx".

У 1945 році Алан Уейн ( Alan Wayne ) представив особливий вид математичного ребуса, іменованого "doubly - true". Такий ребус складається зі слів, що позначають цифри або числа, які також є математичною рівністю. Наприклад: ДВА x ДВА = ЧОТИРИ (зашифровано 739 x 739 = 546121). Пізніше, у 1955 році, Джеймс Хантер (James Alston Hope Hunter) в жовтневому номері газети "Toronto Globe and Mail" для позначення буквених математичних ребусів, у яких букви утворюють осмислені слова чи фрази використовує слово "alphametic". Не дивлячись на те, що з часом, все ж, більше прижилося слово "криптарифм", Джеймса Хантера без перебільшення можна назвати "батьком" сучасного математичного ребусу, творцем найблискучіших математичних головоломок.

Першу згадку про радянський математичний ребус автору проекту "Ребуси українською" вдалося відшукати в книзі видатного популяризатора фізики, математики та астрономії, одного з фундаторів жанру науково-популярної літератури Якова Ісидоровича Перельмана "Занимательная арифметика. Загадки и диковинки в мире чисел" (1926 рік). В одній із глав автор пише: "Те , що я пропоную назвати арифметичними ребусами - цікава гра американських школярів , у нас поки ще зовсім не відома. Англійська назва гри "div - al - et " - скорочення від" division by letters ", тобто поділ за

допомогою букв. Вона полягає в відгадуванні задуманого слова за допомогою вирішення задачі (на ділення)". Пізніше, у 1939, році виходить невелика брошура «Арифметические ребусы» (серія "Дом занимательной науки"), цілком присвячена цій математичній головоломці.

У повоєнний час математичні ребуси регулярно публікують у радянських книгах, журналах і газетах ("Наука и жизнь", "Техника молодёжи", "Юный техник"). Науково-популярний фізико-математичний журнал для школярів і студентів "Квант" практично в кожному номері радує своїх читачів новими математичними загадками.

Наприкінці століття розвиток обчислювальної техніки додав поштовх у дослідженні та розповсюдженні математичних ребусів. Математики і програмісти переклали на "плечі" персональних комп'ютерів рішення загадок і головоломок. Із зростанням популярності мережі Інтернет з'явилися онлайн

сервіси, які

Без помилок не може бути блискучих

перемрг. полегшують не

Емануель Ласкер тільки розв’язання

математичних ребусів, але, навіть, їх створення. [12]

З історії ребусів

У 1783 році англійський художник і гравер Томас Бьюїк (Thomas Bewick) в лондонській друкарні Т.Ходжсона (T.Hodgson) друкує незвичайну Біблію для дітей, в якій події Святого Письма переказуються у формі ребусів. Виконана таким чином Біблія стала іменуватися "ієрогліфічною". У ній деякі слова з тексту замінені картинками з метою переказати історію в прямий, простий і цікавий спосіб. Через кілька років, в 1788 році, американський видавець Ісайя Томас (Isaiah Thomas) видає ієрогліфічну Біблію за океаном. Такі незвичайні ієрогліфічні Біблії стали дуже популярними

наприкінці XVIII століття, оскільки

Як розв'язувати математичні ребуси

Математичні ребуси - чудова гімнастика для розуму. Ось лише деякі основні правила розв'язання цих захоплюючих математичних загадок:

У математичних ребусах складених з літер, кожною буквою зашифрована одна певна цифра: однакові цифри шифруються однією і тією ж буквою, різним цифрам відповідають різні букви.

У ребусах, зашифрованих, наприклад, зірочками, кожен символ може позначати будь-яку цифру від 0 до 9. Деякі цифри можуть повторюватися кілька разів, інші не використовуватись зовсім.

Перед початком розв’язування математичного ребусу з літер (наприклад, криптарифму), переконайтеся, що в ньому використано не більше 10 різних букв. В іншому випадку такий ребус не матиме розв’язків.

Почніть розв’язок ребусу з правила, згідно з яким нуль не може бути крайньою лівою цифрою в числі. Таким чином всі літери і знаки, з яких починається число в ребусі, вже не можуть бути нулем. Коло пошуку потрібних цифр звузиться.

У ході розв’язання відштовхуйтеся від основних математичних правил. Наприклад, множення на нуль завжди дає нуль, а при множенні будь-якого числа на одиницю завжди отримаємо в результаті вихідне число.

Дуже часто математичні ребуси являють собою приклади складання двох чисел. Якщо при додаванні сума має більше знаків ніж доданки, значить сума починається з "1".

Не бійтеся робити помилки. Можливо, вони підкажуть вам вірний хід рішення. Не нехтуйте методом перебору. Деякі ребуси зажадають тривалого поетапного розв’язання, але в підсумку ви будете винагороджені вірною відповіддю і відмінною розминкою для вашої кмітливості.

Математичні ребуси

Поряд з класичними (вербальними) ребусами існують математичні ребуси. Інколи їх ще називають числовими, арифметичними або криптарифмами. Фактично такі ребуси - це приклади звичайних арифметичних дій

(додавання, віднімання, ділення та множення), в яких частина або навіть

всі цифри замінені на крапки, зірочки, літери чи інші символи. Розгадати ребус - означає відновити первісний вигляд математичної рівності.

Нижче наведено приклади математичних ребусів, що поділені на відповідні категорії: додавання та віднімання, множення, ділення та ін. Варто зазначити, що всі перераховані далі математичні ребуси мають лише один вірний розв'язок. [21]

Простий математичний ребус:

A S+ A = MOM 92+9 =101

Простий математичний ребус на додавання:

* * + * = * * 8

9 9 + 9 =1 0 8

Простий жартівливий математичний ребус

A + F A T = A S S 9 + 8 9 1 = 9 0 0

Простий математичний ребус

EAT+THAT=APPLE

819+9219=10038

Класичний математичний ребус Генрі Дьюдені (1924 р.)

SEND+MORE=MONEY

9567+1085=10652

Театральний математичний ребус

ДРАМА+ДРАМА=ТЕАТР

18969+18969=37938

Таємний математичний ребус

КОКА+КОЛА=ВОДА 3930+3980=7910

Вуличний математичний ребус

УДАР+УДАР=ДРАКА 8126+8126=16252

Астрономічний математичний ребус

SATURN+URANUS=PLANETS

546790+794075=1340865

Дорослий математичний ребус

MAN+WOMAN=CH1LD

586+39586=40172

Подвійний ("doubly-true") математичний ребус

THREE+THREE+TWO+TWO+ONE=ELEVEN

84611+84611+803+803+391=171219

Залізничний математичний ребус

ВАГ0Н+ВАГ0Н=П0ТЯГ 35206+35206= 70412

Математичний ребус на додавання

ОХОХО+АХАХА=АХАХАХ

90909+10101=101010

"Авіаційний" математичний ребус

А+АБ+АБВ=БВБ 6+67+674=747

Бібліотечний математичний ребус

КНИГА+КНИГА+КНИГА=НАУКА

28375+28375+28375=85125

Політичний математичний ребус

USA+USSR=PEACE 932+9338=10270

Комп'ютерний математичний ребус

БІТ+БАЙТ=СЛОВО

927+9537=10464 або 937+9527=10464

Подвійний ("doubly-true") математичний ребус 2+3+7=12

TWO+THREE+SEVEN=TVELVE

104+19722+82526=102352 (або 4 і 6 поміняти місцями)

Математичний ребус на додавання

ХАТА+ХАТА+ХАТА+ХАТА+ХАТА+ХАТА=СЕЛО

1545+1545+1545+1545+1545+1545=9270

Гастрономічний математичний ребус

СТРАВА+СТРАВА=ВЕЧЕРЯ

417686+417686=835372

Сільський математичний ребус

КОРОВА+ТРАВА+ДОЯРКА=МОЛОКО

540498+60898=743414

Боксерський математичний ребус

АТАКА+УДАР+УДАР=НОКАУТ

93989+7492+7492=108973

Складний математичний ребус на додавання

AB+BC+CA=ABC

19+98+81=198

Театральний математичний ребус

БАЛЕТ+БАЛЕТ=ТЕАТР 23674+23674=47348

Подвійний ("doubly-true") математичний ребус

ДВА x ДВА = ЧОТИРИ

739 x 739 = 546 121

Математичний ребус на множення TWOxTWO=THREE

138 х 138 =19 044

Лісовий математичний ребус на множення

СОСНА х 7 = ТАЙГА

12 195 х 7 = 85 365

Спортивний математичний ребус на множення ГОЛ х ГОЛ = ФУТБОЛ

425 х 425 =180 625

Математичний "ребус - перевертень" на множення ABCDE х 4 = EDCBA

21 978 х 4 = 87 912

БУКВА х 6 = СЛОВО

10579∙6=63474

Математичний ребус на множення

КУЩI х 9 = ХАЩI

1075 х 9 = 9 675

Чи знаєте ви, що...

Якщо у ребусі предмети, цифри або літери зображені один на одному, то їх назви читаються із додаванням прийменника "на", "над" або "під" (попереду назв або між ними).

Математичний ребус із піднесенням до степеня

Я^с=СІМ'Я

5⁷ = 78 125

Сакральний математичний ребус з піднесенням до степеня

О^ко=СИЛА

2¹² = 4 096

Спортивний математичний ребус з піднесенням до степеня

ГОЛ ² = ФУТБОЛ

425 ² = 180 625

Ребуси в малюнках

1. (Коло)

2. (Сфера)

2 = Е

3. (Площина)

4. (Градус)

5. (Тангенс)

6. (Знаменник)

7. (Кратний)

8. (Операція)

9. (Дріб)

10. (Ордината)

+ Р

11. (Корінь)

12. Відсоток

13. Перетин

14. Куб

15. Одиниця

16. Парність

17. Змінна

+ Н

18. Період

+ І

23. Частка

24. Ділене

ФРАГМЕНТИ УРОЧНОЇ ТА ПОЗАУРОЧНОЇ РОБОТИ

Урок-подорож в країну – многочленів

(7 клас)

Мета уроку: повторення, узагальнення і систематизація знань з теми «Многочлени. Способи розкладання многочленів на множники»; активізація діяльності учнів у ході навчання; підвищення інтересу учнів до вивчення предмета.

Обладнання: мультимедійний проектор, комп’ютер, карточки з завданнями, тестова програма, кубик з завданнями, підручники.

Очікувані результати:

Після уроку учні зможуть:

- узагальнити і систематизувати свої знання про многочлени;

- розкладати многочлени на множники; - поглибити знання з природи. Тип уроку: контроль і корекція знань

Хід уроку

І. Постановка мети і формулювання завдань уроку

Математика - це велична споруда,

створена уявою людини, для пізнання ВСЕСВІТУ

У людини багато потреб. З давніх-давен люди вивчають, досліджують

Всесвіт. Завдяки відкриттям Коперніка і Галілея люди дізналися, що таке

Сонячна система. До її складу входять 9 великих планет: Меркурій, Венера, Земля, Марс, Юпітер, Сатурн, Уран, Нептун, Плутон та їхні супутники, велика кількість малих планет, комет, метеоритів.

Ми з вами відправимося у подорож в Всесвіт. Побувавши на всіх дев’яти планетах і виконавши певні завдання і вказівки, ми дізнаємося де знаходиться наша Сонячна система.

Протягом уроку ви повинні бути уважними, щоб в кінці уроку розгадати і прочитати слово.

І так, тема уроку: «Многочлен. Способи розкладання многочленів на множники».

А тепер я запрошую вас до подорожі.

Роздаю учням прямокутники трьох кольорів.

На протязі всього уроку за активність і за правильно виконані завдання учням роздаю смайлики.

ІІ. Актуалізація опорних знань

Перша наша зупинка – планета Меркурій.

1. Повторення. Слайд 4

Називаєте номер картки і отримуєте запитання. Червоний колір – визначення, жовтий – формула, зелений – приклад.

(За всі правильні відповіді отримуєте літеру).

Запитання:

Одночлен

Многочлен

Многочлен стандартного вигляду

𝑎𝑛 · 𝑎𝑚 = 𝑎𝑛+𝑚

𝑎𝑛: 𝑎𝑚 = 𝑎𝑛−𝑚

(𝑎𝑛)𝑚 = 𝑎𝑛∙𝑚

(𝑎 ∙ 𝑏)^𝑛= 𝑎^𝑛∙ 𝑏^𝑛

𝟐𝒂^𝟑· 𝟎, 𝟒𝒂^𝟓𝑏 =

−𝟎, 𝟔𝒙^𝟓𝒚: 𝟐𝒙𝒚 =

𝟑𝒙^𝟐+ 𝟓𝒙 − (𝟔𝒙^𝟐+ 𝟐𝒙) =

𝟏𝟐𝒎𝒏 · 𝟒𝒎^𝟒𝒏: 𝒎^𝟑=

𝟑𝒄^𝟑(𝒄 − 𝟒) − 𝟐𝒄(𝒄^𝟑− 𝟔𝒄^𝟐+ 𝟐𝒄)=

Друга наша зупинка – планета Венера.

2. Повторимо правило додавання і віднімання многочленів, множення одночлена на многочлен і многочлена на многочлен. Слайд 18

• Щоб помножити одночлен на многочлен, треба помножити цей одночлен на кожний член многочлена і знайдені добутки додати.

• Щоб помножити многочлен на многочлен, треба кожний член першого многочлена помножити на кожний член другого многочлена і отримані добутки додати.

Третя наша зупинка – планета Земля.

Шестеро учнів розв’язують рівняння, записані на гранях «Кубика-

Архімедика». Слайд 20

5x⁵x⁴0

10a²2a0

xx²⁰

4y4y²0 x²25x0

4a²100a0

1) x=0; x=0,2 2) a=0; a=0,2 3) x=0; х=1

4)у=0; у=1 5) х=25; х=0 6)а=0; а=25.

По два рівняння мають однакові розв’язки. Перша пара, яка правильно розв’яже рівняння, отримує смайлики

Решта учнів перевіряють готові завдання і виправляють помилки:

1) (x + 5)(y - 7)=xy + 5y - 7x - 35(+)

2) (3x - 5)(2x + 6)=6x ²- 28x - 30(-)

3) (4x³- x)(2x²+ 3x)=8x⁵+ 12x⁴- 2x³+ 3x(-)

4) (- 2 - y)(y²+ 3)=- y³+ y²+ 3y - 6 (-)

5) (a + b)(a²– ab + b²)=a³- b³(+)

6) (6x + 1)(6x - 1)=36x² + 1(-) Слайд21

Четверта наша зупинка – планета Марс.

Учні об’єднуються у групи за кольорами. Кожній групі роздаю завдання. Гра типу «Пазли». На листку паперу написані завдання і на окремих квадратиках написані відповіді до даних завдань. Учні виконують завдання, вибирають відповіді і прикладають їх на листок з завданнями. Складається картинка. Якщо завдання розв’язані невірно, то картинка не складеться. Завдання: Слайд 24

x(a – b )- y(a - b)=	a(3x – 4y) + b(3x – 4y)=	3x (m – 2n) + 4y(2n – m)=
3a(x – y) – (x – y)=		(x +2)(3y – 1) + (x + 2)(2y – 7)=

Розкладіть на множники:

x(a – b )- y(a - b)= a(3x – 4y) + b(3x – 4y)= 3x (m – 2n) + 4y(2n – m)=

3a(x – y) – (x – y)=

(y – 3 )² – 4 (y – 3)= (x +2)(3y – 1) + (x + 2)(2y – 7)=

Відповіді:

(a-b)(x-y)

(3x-4y)(a+b)

(m-2n)(3x-4y)

(x-y)(3a-1)

(y-3)(y-7)

(x+2)(5y-8)Слайд 25

П’ята наша зупинка – планета Юпітер.

«Шифровка»

Розшифруйте вислів вченого Едісона.

Учні дописують праву частину формули, підбирають слово і розшифровують вислів.

Запишіть замість * такий одночлен, щоб виконувалась рівність:

1. (a +b +c)·*=ax + bx + cx

2. *·(c -m +k) =abc – abm + abk

3. *·(ab – b²) = a³b – a²b²

4. ( x – y)·* =x³y – x²y²

5. (9x²t – 5xt²)· * =18x³t⁷ – 10x²t⁸

6. 5m²·( * - 7mn³) = 15m⁵n – 35 m³n³

Ключ

Навчити	x ²y
Мислити	3m³n
Найважливіше	x
Цивілізації	a 2
Людину	2xt6
Завдання	ab

Слайд 27

Шоста наша зупинка – планета Сатурн.

Завдання в групах.

Учні діляться на 2 групи за кольором. Кожна група отримує завдання, розв’язують, обговорюють і представник з кожної групи розв’язує на дошці і коментує.

1 група:

1. Довести, що 21³14³7³ділиться на 34.

2 група:

2. Довести, що 27³3⁷9³ділиться на 25.

Сьома наша зупинка – планета Уран. (РОЗКЛАДАННЯ МНОГОЧЛЕНА

НА МНОЖНИКИ МЕТОДОМ ГРУПУВАННЯ)

Колективне виконання вправи з підручника № 522. Слайд 30 IV. Завдання додому.

Восьма наша зупинка – планета Нептун. Слайд 32

1. Розв'язати № 531, 535.

2. Завдання для перевірки знань с. 85.

3. Повторити § 10 -15

V. Підсумок уроку

Дев’ята наша зупинка – планета Плутон.

Підсумуємо вивчене на сьогоднішньому уроці та на попередніх уроках.

Що потрібно знати для того, щоб вміти розкладати многочлени на множники?

Учні відповідають.

• Розкласти многочлен на множники означає подати його як добуток кількох многочленів, тотожний даному многочлену.

• Розкласти способом групування:

1. Утворити групи членів, що мають спільний множник;

2. Виносимо за дужки спільний множник у кожній групі;

3. Після цього виносимо за дужки спільний множник для всіх груп.

А тепер подивимося, які літери ми зібрали, побувавши на всіх планетах.

Складемо з цих літер слово. Слово ГАЛАКТИКА.

Слайд 34

Отже, наша Сонячна система знаходиться в галактиці, яка називається Чумацький шлях.

Ви дуже гарно попрацювали на уроці. Надіюсь, що те, що вивчили на уроці ви не забудете і закінчити урок хочу словами французького фізика – інженера Лауе «Освіта є те, що залишається, коли все вивчене вже забуто».

Впевнена, що знання, які ви отримуєте на уроках математики відповідають вимогам часу, в якому ми живемо і будуть вам потрібні.

Оцінюю роботу учнів на уроці по кількості смайликів, які вони збирали протягом уроку.

Дякую всім за урок. До побачення!

Чи далеко тобі до вершини?

На якій ти сходинці

В математиці країні. Для заміток

І сувора й солов’їна

Математика країна. ____________________________________

Праця тут іде завзято

Вмій лиш спритно рахувати.

Вмій ділити, віднімати,

Множить швидко й додавати. Вмій кмітливо все збагнути, Першим в відповіді бути! Ледарів у нас немає, Хто руки не піднімає?

Вирушаймо в путь.

Нас цікаві справи ждуть.

Цифри можна прочитати

І про все на світі знати,

____________________________________

«Математика – цариця наук. Її улюблениця – істина. Її вбрання – простота. Палац цієї володарки оточений тернами. І щоб досягти його, кожному доводиться пробиватися крізь хащі. Краса його відкривається тільки розуму».

Скільки коксу домнам треба ____________________________________ (Ян Снядецький.)

Й про політ космічний в небо,

Скільки зір дрібних, як просо ____________________________________

У веснянок є на носі.

Все умій ти пов’язати, ____________________________________

Про складне й просте сказати.

Наш девіз – все гарно знати, ____________________________________

Вміти добре рахувати.

Виростаймо ж – і у путь. ____________________________________

Хай знання із нами йдуть.

____________________________________

Ну а потім, в результаті, Все, як слід, підсумувати,

____________________________________

Й розділити на усіх ТИЖДЕНЬ

І багатство, й щедрий стіл. ___________________________________

сл. С. Погорєловського

МАТЕМАТИКИ

Понеділок

1.Урочиста лінійка — відкриття. Виступ вчителя: «Ознайомлення з планом проведення тижня математики».

8 :45— 8: 55

2.Конкурс « Кращий малюнок про математику ( учні 5—11 класів).

11 : 45—12: 05

Вівторок

1. Випуск математичних буклетів « У математичній країні» (учні 5-11 класів)

11 :45—12 : 05

2. Гра « Найрозумніші ». ( учні 7—8 класів)

14 : 50—15 : 35

Середа 1. Конкурс « Математична розмальовка». ( учні 1—4 класів)

9 : 00— 13 : 00

2. Презентація «Математика в житті людини»

14: 50—15 : 35

Четвер

1. Математичні головоломки. (учні 5—11 класів).

( на перервах)

2. Математична вікторина ( учні 5—

6 класів)

14 :50—15 : 35

П'ятниця 1. Фільм про математику: «Кравчук—видатний український математик». Презентація буклетів: « У математичній країні»

14 : 50—15 : 20

2. Конкурс « Міс Математика та Містер Математик ». (учні 9—11 класів)

15 : 20—16 : 00

МАТЕМАТИКА КРАЇНА

І сувора й солов’їна

Математика країна.

Праця тут іде завзято Вмій лиш спритно рахувати. Вмій ділити, віднімати, Множить швидко й додавати. Вмій кмітливо все збагнути, Першим в відповіді бути!

Ледарів у нас немає,

Хто руки не піднімає?

Вирушаймо в путь.

Для нотаток:_____________________________

________________________________________ ________________________________________

________________________________________

Бубнівська ЗОШ І – ІІІ ступенів

Тиждень математики

Математику вже тому вчити треба, що вона розум у порядок приводить.

М. В. Ломоносов

Нас цікаві справи ждуть. ________________________________________

Цифри можна прочитати ________________________________________

І про все на світі знати,

Скільки коксу домнам треба ________________________________________

Й про політ космічний в небо, ________________________________________

Скільки зір дрібних, як просо

________________________________________

І веснянок є на носі.

Все умій ти пов’язати, ________________________________________ Про складне й просте сказати. ________________________________________

Наш девіз – все гарно знати,

Вміти добре рахувати. ________________________________________

Виростаймо ж – і у путь. ________________________________________

Хай знання із нами йдуть. ________________________________________

Ну а потім, в результаті,

Все, як слід, підсумувати, ________________________________________

Й розділити на усіх ________________________________________

І багатство, й щедрий стіл.

________________________________________

________________________________________ Підготували: учні 5 класу

________________________________________

Історичні відомості про натуральні числа

Натуральні числа виникли дуже давно. Число – одне з основних понять математики, яке дозволяє виразити результати лічби або вимірювання. Спочатку з’явилися числа 1 і 2 , трохи пізніше – 3. Комбінуючи ці числа, отримували числа до шести. А про все, що більше за шість, казали «багато».

Це виражено в прислів’ях та приказках, де число 7 виступає синонімом слова «багато»: «Семеро одного не ждуть», «Сім раз відмір один раз відріж», «Один із сошкою, а семеро із ложкою».

З плином часу люди навчилися облічувати все більші і більші кількості. Довго вважалося, що існує якесь найбільше число.

Наші пращури називали найбільше число «колода» і вважали його рівним 1096. При цьому додавався коментар: «Етого же чесла несть болем разу мети человеку». І лише згодом люди зрозуміли, що найбільшого числа немає.

Отже,

натуральні

числа – це числа, які

виникають при рахунку, нумерації і перерахуванні предметів. До них не відносяться негативні і нецілі числа, тобто раціональні, речові та інші.

До визначення натуральних чисел виділяють два підходи. По-перше, це числа, які використовуються при перерахуванні предметів або при їх нумерування (п'ятий, шостий, сьомий). По-друге, при позначенні кількості предметів (один, два, три).

Безліч натуральних чисел нескінченно, тому що для будь-якого натурального числа знайдеться інше натуральне число, яке буде більше.

Перевір себе:

1. Скільки десятків в числі 2 689?

a) 6

b) 89

c) 8

2. Скільки сотень в числі 7 650?

a) 7

b) 65

c) 6

3. Яке число в натуральному ряді стоїть за числом 240?

a) 239

b) 241

c) 250

4. Яке число в натуральному ряді передує числу 61?

a) 60

b) 59

c) 51

5. Яке з поданих чисел є найменшим трьохзначним числом?

a) 33

b) 100

c) 101

6. Яке з поданих чисел є найбільшим чотирьохзначним числом?

a) 4989

b) 4999

c) 9999

7. Порівняйте величини: 1 000 см і 12 м.

a) 1 000см = 12 м

b) 1 000см > 12м

c) 1 000см < 12 м

8. Порівняйте величини 10 кг 500 г і 15 000 г.

a) 10 кг 500г = 15 000г

b) 10 кг 500г > 15 000г

c) 10 кг 500г < 15 000г

9. Яке з чисел найбільше: 107, 46, 12, 38, 201?

a) 107

b) 12

c) 201

Про «плюс» і «мінус» Віднімання з додаванням Загадки — добавлянки

Не чужі, а навпаки.

Як відомо вони мають

Тісні та міцні зв'язки .

Треба вам число відняти?

Можна замість того

Протилежне додати — Тут нема важкого.

Ці числа є великі,

А є і малюки,

Проте з них кожен має

Цілі числа

І частки знак так само

Ми можемо знайти,

А модулі поділиш — І частку знаєш ти !

Сума цих двох чисел

Є у нас нулем.

( Протилежні числа.)

Н. Вінтер

Учні 6 класу

Але тут факт дивний маєш: Лише два дільники.

Як від'ємне віднімаєш, Як відомо числа ці

То число, яке в нас є, Називаються … .

Більшим від чогось стає! ( Прості.)

Від'ємні числа множити

Цікаво й фантастично, Нам ці числа треба знати,

Бо результати множення Щоб від двох п'ятсот відняти.З ними дія додавання —

Виходять нам незвичні.

Як множиш ти «два мінуси» - Це суцільне здивування.Все одно вони приємні,

Одержиш «плюс» раптово,

Помножиш «плюс» на «мінус» - Числа на ім'я … . ( Від'ємні )

Виходить «мінус» знову.

А з модулем добутку

Відсутня в нас турбота:

Лиш перемножив модулі — Із сумою цих чисел

І вся твоя робота! Немає в нас проблем:

Деякі історичні

відомості про

Перші писемні пам'ятки про числа зустрічаються за кілька тисяч років до нашої ери.

В історії науки додатні та від'ємні кількості вперше

розрізняли в Китаї ще в І ст. до н. е. Додатні числа в Китаї називали «чен»

(червоний), а від'ємні - « фу» (чорний). Лише в середині ХІІІ ст. Лі Є запропонував позначати від'ємні числа цифрами, перекресленими справа наліво.

У Європі до ідеї від'ємної кількості досить близько підійшов у ХІІІ ст. Л. Пізанський. Сучасне позначення від'ємного числа знаком « - » наприкінці ХV ст. увів німецький математик Відман (1460 –1530).

Широкого застосування в Європі від'ємні числа набули завдяки Р. Декарту (1595—1632) і П.

Ферма (1601—1665).

Додавання раціональних чисел

з різними знаками.

Знову ми зустрілися з бідою… Суму чисел треба нам знайти. Та от знаки в них не однакові, Просимо нам допомогти. І підручники ми відкриваємо, Правило там читаємо:

Щоб додати два числа,

Знаки яких різні, треба

Модуль більшого з них відшукати,

Від нього модуль меншого відняти,

А перед різницею модулів цих

Поставити знак модуля більшого з них.

Віднімання раціональних чисел.

Відняти два числа навчиться той, Хто з додаванням дружить. Ти до зменшуваного додай

Число протилежне від'ємника, друже.

Додавання раціональних чисел з однаковими знаками.

У нас задача не легка —

Додати треба два числа. Два числа не натуральні, Вони в нас раціональні!

Плюс за мінус забігає,

Плакати не починає,

Тихенько сідайте і запам'ятайте: Якщо числа однакові знаки мають, То їх модулі додай.

Та суму їх не ображай —

Знак цих чисел перед нею поставити поспішай..

Властивості додавання і множення.

Щоб легко множити і додавати, Закони ти повинен пам'ятати . Переставний або комутативний: a + b = b + a, ab = ba. Сполучний: (a+b) + c = a+(b+c)= (a+c)+b, Розподільний : a(b+c)= ab+ac.

Геометрія – чудова країна. Все є в цій країні,і таке цікаве життя,якого немає ні в одній галузі науки. Чому? Геометрію утворюють такі різні фігури і скільки вони мають елементів,властивостей,що в інших науках виникає заздрість,але заздрість здорова,адже всі знають,що Геометрія – велика трудівниця. Постійно і плідно працюють всі її фігури, від найпростіших до найскладніших.

А що відбувається у кожній фігурі?

Цікаво дізнатися?

Трикутник, як і кожна фігура, є фортецею, де сторони – стіни, вершини – сторожові вежі. Усі точки трикутника мешкають у цій фортеці. На жаль,точки не можуть вийти з фортеці,але вони звикли до такого життя і дуже раділи,коли відбувалося що – небудь в їх маленькому князівстві. Що робили точки? Вони вивчали свої властивості і пропонували їх для розв’язування задач,побудови будь – яких елементів у трикутнику. Наприклад, зібралися усі точки рівновіддалені від двох сторін трикутника і виявили, що всі вони лежать на одному відрізку,на чудовому відрізку – бісектрисі кута трикутника. Ось така чудова родина виявилась. І таких родин було аж три. Усі точки бісектриси пишалися такою властивістю: от ми які! Одна точка,що мешкала одразу на трьох бісектрисах,вважала себе головною серед інших точок. І на те була причина: вона була центром писаного кола. Але інші точки мали багато цікавих властивостей. І знайшлися такі, що довели: вони теж відносяться до головних точок. Це точки, які були одночасно точками бісектрис і сторін трикутника. Що цікавого було у цих точок? Вони ділили сторону на відрізки,пропорційні до двох інших сторін. І таке чудове відношення зберігалося на кожній стороні трикутника.

Цю властивість перевірили на інших трикутниках, і всі перевірки підтвердили її. От які важливі точки є у трикутнику.

Трикутник, що рівні сторони всі має, Рівностороннім називаємо. Трикутник, що прямий кут має, Прямокутним називаємо.

Види трикутників за кутами

Ось трикутник перед нами З трьома гострими кутами. Незалежно від сторін Гострокутним зветься він.

Ось трикутник інший тут, Є тупий у нього кут.

Що тут думати гадати? Тупокутним слід назвати.

Ось з прямим кутом трикутник – Багатьох задач супутник. Прямокутний– назва в нього, У трикутника такого.

ГЕОМЕТРІЯ

Ох, не легко це дається:

Математичні цікавинки

В автобусі їде жінка з онуком. Він голосно запитує: — Ба, а скільки тобі років? Вона намагається ухилитися від відповіді. Він:

— Ба, ну скажи першу цифру.

— П’ять.

— А другу? — Чотири.

— А третю?

\\\\

Яка різниця між шизофреником і неврастеніком?

Шизофреник упевнений, що 2*2=5, і спокійний, а неврастенік знає, що 2*2=4, і нервує.

\\\\

Жидівському хлопчику задають задачу: — Ти маєш шість яблук. Якщо ти віддаси половину брату, скільки залишиться? — П’ять із половиною.

Потренуй розум

1. Провести осі координат, вибрати одиницю довжини на осях, Побудувати точки з координатами:

(1;2), (-2;1), (-1;3), (2;-1).

2. Взяти будь-які чотири точки на координатній площині. Знайти координати цих точок.

3. З точки A(2;3) на вісь Ox опущено перпендикуляр. Знайти координати основи перпендикуляра.

4. Знайти відстань від точки A(-3;4) до:

а) осі Ox;

б) осі Oy;

в) до початку координат.

5.Побудуйте трикутник,

симетричний даному з вершинами

А(2; 4) , В(4; -6),

С( -1;-5 ,) відносно початку координат

ГЕОМЕТРИЧНІ ПЕРЕТВОРЕННЯ

Дещо з історії

Леонардо да

Вінчі:народився 15 квітня 1452 року у селищі Анкіано поблизу Вінчі.

Приблизно з

15років навчався у майстерні Верроккіо. Майстерня Верроккіо містилась в інтелектуальному центрі тодішньої Італії,в місті Флоренції,що дозволило Леонардо навчитися гуманітарнх наук,а також деяких технічних знань.

Леонардо да Вінчі захоплювався багатьма мистецтвами. Зокрема він був художником,скульптором,інженеро

м.

Він малював чудові картини,відомими картинами є «Мона Ліза», або» Джаконда», також є ціла збірка картин Мадон.

Найкращим прикладом просторового зображення є

«Вітрувіанська людина»

уславлений малюнок, який іноді називають канонічними пропорціями

Судоку

У кожну клітинку впиши числа 1, 2, 3, 4 так, щоб у кожних рядку, стовпчику і

«Вітрувіанська людина» -

Дещо з історії

Здавна відомі п'ять правильних багатогранників(так званих платонових тіл):

тетраедр, гексаедр(куб),додекаедр, ікосаедр.Так назвали їх стародавні греки. Окрім правильних багатогранників існують ще й інші тіла, що вабили вчених своєю гармонійністю. Знаменитий німецький астроном Йоганн Кеплер пропонував модель побудови Всесвіту , що складалася з правильних багатогранників і вписаних у них сфер,так званий «кубок Кеплера». За Кепрела зовнішня велика сфера відповідає орбіті найвіддаленішої з відомих на той час планети Сатурна. Якщо в цю сферу вписати куб, а в куб знову сферу то це буде сфера орбіти Юпітера. У сферу Юпітера Кеплер вписує правильний тетраедр, а вписана в нього сфера відповідає орбіті Марса. У сферу Марса вписується додекаедр і знову сфера відповідає орбіті Землі. Далі вписується ікосаедр і сфера Венери, а після того октаедр і сфера орбіти Меркурія. Пізніше саме Кеплер відкрив, що траєкторія руху планет навколо Сонця є не кола, а еліпси і «кубок Кеплера» а разом із ним і правільні багатогранники втратили ореол таємничості.

Архімедові тіла – напівправильні опуклі многогранники, в яких всі двогранні кути рівні , а грані - правильні многокутники різних типів.

Малий зірковий додекаедр

Великий додекаедр

Великий зірковий додекаедр

Великий ікосаедр

Література

1. Бевз Г. П. Алгебра: підручник для 7 класу загальноосвіт. навч. закл. / Г. П. Бевз, В. Г. Бевз – К.: Видавництво «Відродження», 2015. – 288с.

2. Брославська . Г. Кросворд «Многогранники. Тіла обертання » / Г.

Брославська // Математика. Шкільний світ. – 2009. – № 24. – С. 22 .

3. Бурда М. І. Геометрія: Підручник для 9 класу загальноосвіт. навч. закл. /

М. І. Бурда., Н. А. Тарасенко – К.: Зодіак-ЕКО, 2009

4. Брославська . Г. Кросворди / Г. Брославська // Математика. Шкільний світ. – 2012. – № 4. – С. 17 -23.

5. Брославська . Г. Кросворд до теми "Многогранники. Тіла обертання" / Г.

Брославська // Математика. Шкільний світ. – 2008. – № 3. – С. 24.

6. Брославська Г. Кросворди до теми "Многогранники. Тіла обертання" / Г.

Брославська // Математика. Шкільний світ. – 2007. – № 8. – C. 24 .

7. Брославська, Г. Кросворди до теми "Многогранники. Тіла обертання" / Г.

Брославська // Математика. Шкільний світ. – 2007. – № 12. – С. 22 -23.

8. Брославська, Г. Кросворд"Функція " / Г. Брославська // Математика.

Шкільний світ. – 2012. – № 1 -2. – С. 36 -37.

9. Демчук . О . Кросворди / О . Демчук // Математика. Шкільний світ. – 2011.

– № 45. – С. 20 -23.

10. Думанська Г.О. Застосування комп’ютерних технологій у навчальному процесі /Г. О. Думанська // Математика в школах України. – 2009.- № 4. – с.2.

11. Іванців . О. Кросворд з геометрії / О. Іванців // Математика. Шкільний світ. – 2009. – № 14. – С. 17 .

12. Корнієнко Т. Л. Тиждень математики в школі 5 – 11 класи / Т. Л.

Корнієнко, В. Л. Фіготіна. – 3-тє вид. – Х.: Веста, 2010. – 176 с.

13. Кулага Г. С. Угорські кросворди на уроках геометрії в 7 класі / Г. С.

Кулага // Математика в школах України. – 2014. - №34-36. – С. 96-98.

14. Лисенко . О. Математичні кросворди 5 клас / О. Лисенко, Ю. Юхта // Математика. Шкільний світ. – 2008. – № 9. – C. 24 .

15. Лисенко, О. Математичні кросворди /О.Лисенко, Ю.Юхта // Математика.

Шкільний світ. – 2008. – № 39. – С. 22 .

16. Литвиненко Т . Математика в кросвордах / Т . Литвиненко // Математика.

Шкільний світ. – 2011. – № 29. – С. 18 -22.

17. Мерзляк А. Г., Полонський В. Б., Якір М. С. Алгебра: Підручник для 9 класу. – Х.: Гімназія, 2009.

18. Наконечна А . Математичні кросворди / А. Наконечна // Математика.

Шкільний світ. – 2008. – № 10. – С. 21 .

19. Пушкіна З. П. Математичні кросворди / Пушкіна З.П // Математика в школах України – 2014.– № 3. – С. 32.

20. Хохлова Н. І. Математичні кросворди / Хохлова Н.І // Математика в школах України . – 2014. – № 22 -23. – С. 73 - 76.

21. http:// rebus1.com

Для нотаток

Для нотаток Для нотаток Не помиляється лише той, хто нічого не робить. Але й нічого не робити — помилка.

Еміль КРОТКІЙ

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 2

Оцінки та відгуки

Шмагун Наталія 02.06.2023 в 22:24

Щиро дякую!

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Нєборська Олена Анатоліівна 02.03.2021 в 09:46

Дуже цікава розробка, реальна допомога в організації заходів до Тижня математики

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

pdf

Завантажити

Зберегти на потім

Додав(-ла)

Юхно Мирослава Анатоліївна

Пов’язані теми

Математика, Методичні рекомендації

Додано

12 лютого 2019

Переглядів

24950

Оцінка розробки

5.0 (2 відгука)

З	М	Е	Н	Ш	У	В	А	Н	Е
Д	Н	У	М	Е	Р	А	Ц	І	А
О	Ц	И	Ф	Р	А	С	У	М	Я
Д	Н	А	+	В	=	В	+	А	О
А	У	А	Л	М	М	L	А	Т	Д
Н	Р	Н	Ь	І	Н	У	Л	Ь	И
К	В	І	Д'	Є	М	Н	И	К	Н
И	П	О	Р	І	В	Н	Я	Т	И

О	П	О	К	А	З	Н	И	К	Н	С	К
С	К	В	А	Д	Р	А	Т	К	У	Б	Н
Н	Д	І	Л	Ь	Н	И	К	О	Н	Д	С
О	Н	Е	П	А	Р	Н	Е	Ь	С	Т	Д
В	П	А	Р	Н	Е	К	Р	А	Т	Н	Е
А	С	Т	Е	П	І	Н	Ь	Л	І	І	П

С	В	І	Д	Н	О	Ш	Е	Н	Н	Я
Е	П	Р	О	П	О	Р	Ц	І	Я	К
Р	Р	І	В	Н	І	С	Т	Ь	А	Р
Е	Ч	Д	І	А	Г	Р	А	М	А	А
Д	К	Л	І	Н	І	Й	Н	А	С	Й
Н	Т	С	Е	К	Т	О	Р	Н	А	Н
І	С	Т	О	П	Ч	А	С	Т	А	І
В	Л	А	С	Т	И	В	І	С	Т	Ь

Г	Е	О	О	И	Н	Ь	Т	Я
Т	О	М	Д	Й	Ч	Т	Р	І
К	Ч	Е	И	Н	И	И	И	Р
А	П	Т	Р	І	Я	Ж	Е	Т
О	Р	Р	І	З	О	А	Л	Е
М	І	Д	М	А	К	Н	А	М
І	В	Р	Я	О	Щ	И	Н	І
Н	Ь	П	П	Л	П	Л	А	Н

К	К	В	А	Н	Ь	К	Ш
У	Б	А	Т	Т	Н	И	В
А	Р	Д	С	У	К	Д	И
Т	В	І	Д	К	І	К	О
П	Р	Я	М	О	С	О	Л
К	Р	И	И	К	Т	А	С
Р	Т	К	Н	П	Ь	Ч	А
У	Г	У	Т	Р	И	З	М

Г	С	У	Н	М	І	Н	І
О	Е	К	Д	А	І	У	Н
С	Т	Р	И	Й	Н	Т	Ь
Т	С	У	М	І	Ж	А	Л
У	В	Е	Р	Т	И	К	А
П	И	Й	И	Н	И	С	А
П	Г	О	Ш	А	Р	Р	О
Р	З	Р	Р	Б	Т	Т	П
Я	О	Н	Е	І	К	И	С
М	Р	У	В	С	Е	Р	Н
И	Й	Т	И	Й	Т	Р	А

П	П	Е	Р	П	Е	Н	Д	И	К
Е	С	О	З	Я	В	И	С	Н	У
Р	І	Т	Н	Н	Е	В	К	О	Л
П	Ч	Е	А	Н	М	О	Л	В	Я
Е	Н	О	Ч	Е	У	В	І	О	Р
Н	А	Р	А	К	С	А	Д	К	Н
Д	І	Е	М	А	І	О	М	А	І
И	Н	Ь	Л	Е	Л	А	Р	А	П
К	У	Л	Я	Р	Н	І	С	Т	Ь

М	Е	Д	І	С	Е	К	Т
П	Т	І	Б	В	И	С	Р
Р	Р	А	Н	А	Й	О	И
Я	И	У	Т	Н	И	Т	С
М	О	К	О	Б	Е	А	А
Р	І	В	Н	К	Д	Р	Е
Р	Г	І	Н	А	Т	Е	Н
І	І	Ш	В	О	З	Т	И
В	П	Н	І	Й	З	А	Й
Н	О	Т	Е	Н	У	Й	І
О	С	Т	О	Р	О	Н	Н

Т	Р	І	В	Н	О	Б	Е	Д
Р	Ц	Е	Н	Т	П	Е	Р	Р
И	К	У	Т	Р	Е	Н	И	Е
О	Е	Н	Н	О	Ц	Т	М	Н
Р	Ц	Т	И	Ї	Н	Р	Е	И
Т	О	Р	К	Д	І	Р	Т	Й

К	Р	А	Д	К	О	Н	Ц
О	Л	О	І	О	Т	И	Е
Х	О	Р	У	Д	С	Ч	Н
М	Е	Д	С	Ь	І	Н	Т
А	Т	А	У	Л	Ч	А	Р
І	Р	Р	К	А	Н	А	И
Д	Ц	И	Д	В	І	Н	Ч

З	М	Е	Н	Ш	У	В	А	Н	Е
Д	Н	У	М	Е	Р	А	Ц	І	А
О	Ц	И	Ф	Р	А	С	У	М	Я
Д	Н	А	+	В	=	В	+	А	О
А	У	А	Л	М	М	L	А	Т	Д
Н	Р	Н	Ь	І	Н	У	Л	Ь	И
К	В	І	Д'	Є	М	Н	И	К	Н
И	П	О	Р	І	В	Н	Я	Т	И

О	П	О	К	А	З	Н	И	К	Н	С	К
С	К	В	А	Д	Р	А	Т	К	У	Б	Н
Н	Д	І	Л	Ь	Н	И	К	О	Н	Д	С
О	Н	Е	П	А	Р	Н	Е	Ь	С	Т	Д
В	П	А	Р	Н	Е	К	Р	А	Т	Н	Е
А	С	Т	Е	П	І	Н	Ь	Л	І	І	П

С	В	І	Д	Н	О	Ш	Е	Н	Н	Я
Е	П	Р	О	П	О	Р	Ц	І	Я	К
Р	Р	І	В	Н	І	С	Т	Ь	А	Р
Е	Ч	Д	І	А	Г	Р	А	М	А	А
Д	К	Л	І	Н	І	Й	Н	А	С	Й
Н	Т	С	Е	К	Т	О	Р	Н	А	Н
І	С	Т	О	П	Ч	А	С	Т	А	І
В	Л	А	С	Т	И	В	І	С	Т	Ь

Г	Е	О	О	И	Н	Ь	Т	Я
Т	О	М	Д	Й	Ч	Т	Р	І
К	Ч	Е	И	Н	И	И	И	Р
А	П	Т	Р	І	Я	Ж	Е	Т
О	Р	Р	І	З	О	А	Л	Е
М	І	Д	М	А	К	Н	А	М
І	В	Р	Я	О	Щ	И	Н	І
Н	Ь	П	П	Л	П	Л	А	Н

К	К	В	А	Н	Ь	К	Ш
У	Б	А	Т	Т	Н	И	В
А	Р	Д	С	У	К	Д	И
Т	В	І	Д	К	І	К	О
П	Р	Я	М	О	С	О	Л
К	Р	И	И	К	Т	А	С
Р	Т	К	Н	П	Ь	Ч	А
У	Г	У	Т	Р	И	З	М

Г	С	У	Н	М	І	Н	І
О	Е	К	Д	А	І	У	Н
С	Т	Р	И	Й	Н	Т	Ь
Т	С	У	М	І	Ж	А	Л
У	В	Е	Р	Т	И	К	А
П	И	Й	И	Н	И	С	А
П	Г	О	Ш	А	Р	Р	О
Р	З	Р	Р	Б	Т	Т	П
Я	О	Н	Е	І	К	И	С
М	Р	У	В	С	Е	Р	Н
И	Й	Т	И	Й	Т	Р	А

П	П	Е	Р	П	Е	Н	Д	И	К
Е	С	О	З	Я	В	И	С	Н	У
Р	І	Т	Н	Н	Е	В	К	О	Л
П	Ч	Е	А	Н	М	О	Л	В	Я
Е	Н	О	Ч	Е	У	В	І	О	Р
Н	А	Р	А	К	С	А	Д	К	Н
Д	І	Е	М	А	І	О	М	А	І
И	Н	Ь	Л	Е	Л	А	Р	А	П
К	У	Л	Я	Р	Н	І	С	Т	Ь

М	Е	Д	І	С	Е	К	Т
П	Т	І	Б	В	И	С	Р
Р	Р	А	Н	А	Й	О	И
Я	И	У	Т	Н	И	Т	С
М	О	К	О	Б	Е	А	А
Р	І	В	Н	К	Д	Р	Е
Р	Г	І	Н	А	Т	Е	Н
І	І	Ш	В	О	З	Т	И
В	П	Н	І	Й	З	А	Й
Н	О	Т	Е	Н	У	Й	І
О	С	Т	О	Р	О	Н	Н

Т	Р	І	В	Н	О	Б	Е	Д
Р	Ц	Е	Н	Т	П	Е	Р	Р
И	К	У	Т	Р	Е	Н	И	Е
О	Е	Н	Н	О	Ц	Т	М	Н
Р	Ц	Т	И	Ї	Н	Р	Е	И
Т	О	Р	К	Д	І	Р	Т	Й

К	Р	А	Д	К	О	Н	Ц
О	Л	О	І	О	Т	И	Е
Х	О	Р	У	Д	С	Ч	Н
М	Е	Д	С	Ь	І	Н	Т
А	Т	А	У	Л	Ч	А	Р
І	Р	Р	К	А	Н	А	И
Д	Ц	И	Д	В	І	Н	Ч

З	М	Е	Н	Ш	У	В	А	Н	Е
Д	Н	У	М	Е	Р	А	Ц	І	А
О	Ц	И	Ф	Р	А	С	У	М	Я
Д	Н	А	+	В	=	В	+	А	О
А	У	А	Л	М	М	L	А	Т	Д
Н	Р	Н	Ь	І	Н	У	Л	Ь	И
К	В	І	Д'	Є	М	Н	И	К	Н
И	П	О	Р	І	В	Н	Я	Т	И

О	П	О	К	А	З	Н	И	К	Н	С	К
С	К	В	А	Д	Р	А	Т	К	У	Б	Н
Н	Д	І	Л	Ь	Н	И	К	О	Н	Д	С
О	Н	Е	П	А	Р	Н	Е	Ь	С	Т	Д
В	П	А	Р	Н	Е	К	Р	А	Т	Н	Е
А	С	Т	Е	П	І	Н	Ь	Л	І	І	П

С	В	І	Д	Н	О	Ш	Е	Н	Н	Я
Е	П	Р	О	П	О	Р	Ц	І	Я	К
Р	Р	І	В	Н	І	С	Т	Ь	А	Р
Е	Ч	Д	І	А	Г	Р	А	М	А	А
Д	К	Л	І	Н	І	Й	Н	А	С	Й
Н	Т	С	Е	К	Т	О	Р	Н	А	Н
І	С	Т	О	П	Ч	А	С	Т	А	І
В	Л	А	С	Т	И	В	І	С	Т	Ь

Г	Е	О	О	И	Н	Ь	Т	Я
Т	О	М	Д	Й	Ч	Т	Р	І
К	Ч	Е	И	Н	И	И	И	Р
А	П	Т	Р	І	Я	Ж	Е	Т
О	Р	Р	І	З	О	А	Л	Е
М	І	Д	М	А	К	Н	А	М
І	В	Р	Я	О	Щ	И	Н	І
Н	Ь	П	П	Л	П	Л	А	Н

К	К	В	А	Н	Ь	К	Ш
У	Б	А	Т	Т	Н	И	В
А	Р	Д	С	У	К	Д	И
Т	В	І	Д	К	І	К	О
П	Р	Я	М	О	С	О	Л
К	Р	И	И	К	Т	А	С
Р	Т	К	Н	П	Ь	Ч	А
У	Г	У	Т	Р	И	З	М

Г	С	У	Н	М	І	Н	І
О	Е	К	Д	А	І	У	Н
С	Т	Р	И	Й	Н	Т	Ь
Т	С	У	М	І	Ж	А	Л
У	В	Е	Р	Т	И	К	А
П	И	Й	И	Н	И	С	А
П	Г	О	Ш	А	Р	Р	О
Р	З	Р	Р	Б	Т	Т	П
Я	О	Н	Е	І	К	И	С
М	Р	У	В	С	Е	Р	Н
И	Й	Т	И	Й	Т	Р	А

П	П	Е	Р	П	Е	Н	Д	И	К
Е	С	О	З	Я	В	И	С	Н	У
Р	І	Т	Н	Н	Е	В	К	О	Л
П	Ч	Е	А	Н	М	О	Л	В	Я
Е	Н	О	Ч	Е	У	В	І	О	Р
Н	А	Р	А	К	С	А	Д	К	Н
Д	І	Е	М	А	І	О	М	А	І
И	Н	Ь	Л	Е	Л	А	Р	А	П
К	У	Л	Я	Р	Н	І	С	Т	Ь

М	Е	Д	І	С	Е	К	Т
П	Т	І	Б	В	И	С	Р
Р	Р	А	Н	А	Й	О	И
Я	И	У	Т	Н	И	Т	С
М	О	К	О	Б	Е	А	А
Р	І	В	Н	К	Д	Р	Е
Р	Г	І	Н	А	Т	Е	Н
І	І	Ш	В	О	З	Т	И
В	П	Н	І	Й	З	А	Й
Н	О	Т	Е	Н	У	Й	І
О	С	Т	О	Р	О	Н	Н

Т	Р	І	В	Н	О	Б	Е	Д
Р	Ц	Е	Н	Т	П	Е	Р	Р
И	К	У	Т	Р	Е	Н	И	Е
О	Е	Н	Н	О	Ц	Т	М	Н
Р	Ц	Т	И	Ї	Н	Р	Е	И
Т	О	Р	К	Д	І	Р	Т	Й

К	Р	А	Д	К	О	Н	Ц
О	Л	О	І	О	Т	И	Е
Х	О	Р	У	Д	С	Ч	Н
М	Е	Д	С	Ь	І	Н	Т
А	Т	А	У	Л	Ч	А	Р
І	Р	Р	К	А	Н	А	И
Д	Ц	И	Д	В	І	Н	Ч