Міністерство освіти і науки, молоді та спорту України

Донецький національний університет економіки і торгівлі

імені  Михайла Туган-Барановського

 

Краматорський коледж

 

 

 

 

Методична розробка

практичного заняття

 

Дисципліна: Вища математика

 

Тема: «Дослідження функції за допомогою похідної і побудова її графіка»

Спеціальність: 076 «Підприємництво, торгівля та біржова діяльність»

за ОПП  «Економіка підприємства»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2020

 

                                    

ЗМІСТ

 

1. Вступ………………………………………………………………………………...3
2. Методика проведення практичного заняття за темою  «Дослідження функції за допомогою похідної і побудова її графіка»
   • План заняття…………………………………………………………………………4
   • Зміст  заняття …………………………………………………………….………….5
   • Методичне обґрунтування проведення заняття…………………………………...6
   • Література…………………………………………………………………………....7

3. Додатки

1.          Талон самоконтролю…………………………………………………………..8
2.          Інструкційна карта……………………………………………………………..9
3.          Інтелектуальна карта……………………………………………………….....17
4.          Зразок домашнього завдання………………………………………………...19
5.          Таблиця-тест  для перевірки знань………………….……………………….20
6.          Графік швидкості змінення попиту при зміні ціни…………………………21
7.          Завдання щодо проведення  самостійної роботи…………………………...22
8.          Критерії  оцінки знань студентів ……………………………………………23

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

 

Аналіз сучасних тенденцій розвитку методів навчання показує, що усі вони поєднуються давно відомими принципами. Відповідно до принципів активності, нічого не може бути «вкладено» у голову студента викладачем. Методика повинна бути побудована так, щоб стимулювати студентів до власних активних дій, спрямованих на процес засвоєння.  «Звичайний викладач підносить істину, гарний − учить їх знаходити», − дані слова А. Дистервега актуальні і сьогодні.

Традиційні принципи, форми, методи і технології у вищих навчальних закладах залишаються основними і використовуються в повсякденній роботі викладача. Активні й інтенсивні технології навчання визначаються інтенсивністю подачі матеріалу, активною позицією і самостійністю студентів, постійним самоконтролем і самокорекцією, проблемністю.

Використання комп’ютерних програм  сприяє активізації уваги і мислення студентів, виховує відповідальність і  навички колективної роботи.  Безперечною перевагою розв’язання задач за допомогою комп’ютера , як і  іншого методу активного навчання,   є змушена активність студентів, що сприяє поліпшенню якості практичної підготовки, тобто більш ефективному досягненню кінцевої мети навчального процесу.

Немаловажними факторами у виборі форм  проведення  практичних занять з предмету «Вища математика» при підготовці молодших фахівців зі спеціальності   «Економіка підприємства» є не тільки тема, мета, навчальний матеріал, але і рівень підготовленості студентів.   Актуальним  залишається підбір завдань з урахуванням особливостей  професії. Важливо показати студентам, що при рішенні економічних задач може бути застосовано математичний апарат. Іншими словами при вивченні різних тем вищої математики формується у студентів уміння застосовувати математичне моделювання при рішенні економічних задач.

Проведення практичного заняття з використанням комп’ютерних програм дозволяє активізувати мислення, втягнути в роботу більшу частину студентів групи, сприяє розвитку інтересу до досліджуваного предмета, додає навчальному процесу розмаїтість. 

Мета  методичної розробки показати методику проведення  практичного заняття з теми  «Дослідження функції і побудова її графіка за допомогою похідної» з використанням пакету прикладних програм MathCAD .

 

 

 

 

 

 

 

 

План заняття

 

Дисципліна:   Вища математика.

Тема заняття:  «Дослідження функції за допомогою похідної

і побудова її графіка».

Вид заняття:   практичне  з використанням пакету прикладних

          програм MathCAD.

Тип заняття: Узагальнення та систематизації знань.

Дата проведення:   12.12.2011р.

Група:   ЕП-11-Б.

 

Мета проведення заняття:

 

методична:  Показати використання адаптивної системи навчання на занятті узагальнення та систематизації знань.

 

дидактична: Узагальнити та систематизувати знання студентів з теми «Дослідження функції і побудова її графіка за допомогою похідної». Ознайомити студентів з можливостями ППП MathCAD у  дослідженні функцій. Розвивати світогляд студентів, інтерес до математики; сприяти розвиткові логічного мислення; навчати прийомів самоконтролю та взаємоконтролю.

 

виховна: Виховувати культуру математичної мови, ерудованість та наполегливість, взаємодопомогу, відповідальність.

 

Міждисциплінні зв'язки:

 

 Забезпечуючі:  математика, інформатика та комп’ютерна техніка.

 

 Забезпечувані:  економіка підприємства, бухгалтерський облік.

 

Матеріально-технічне та методичне забезпечення заняття:

 

Технічне забезпечення: персональний комп’ютер, документ-камера, пакет прикладних програм MathCAD, мультимедійний проектор.

 

Методичне забезпечення: картки самоконтролю, інструкційні карти,  інтелектуальні картки.

 

 

Зміст заняття

1.  Організаційний момент

 

1.       Перевірка наявності студентів в аудиторії.
2.       Перевірка готовності студентів до проведення заняття.
3.       Підготовка дощки до проведення заняття.
4.       Роздача  інструкційних та  інтелектуальніих  карток  та  карток  самоконтролю.  (Додаток 1, 2, 3).

 

2.  Повідомлення теми заняття й ознайомлення з порядком проведення

Тема: «Дослідження функції і побудова її графіка за допомогою похідної».

 

3.  Мотивація пізнавальної діяльності студентів

Поняття похідної-фундаментальне поняття математичного аналізу, за допомогою якого досліджуються процеси і явища в природних, соціальних і економічних науках.

Однією із основних задач математики є дослідження функції. Використання похідної значно полегшує задачу дослідження функції, а разом з тим і побудови її графіка.

При застосуванні ППП MathCAD студенти получають можливість використовувати знання, одержані при вивченні дисципліни «Інформатика».  ППП MathCAD  дає можливість будувати графіки, обчислювати похідну та ін .

Правильність розв’язання можливо перевірити у MathCAD. Для цього необхідно скористатися  правилами знаходження экстремуму функції, засобами математичного аналізу. Знайти похідну функції і розв’язати одержане рівняння допоможуть панелі “Калькулус” і “Символіка”. На занятті ми будемо досліджувати і будувати функції не тільки за допомогою диференціального числення, але й за допомогою можливостей MathCAD. 

 

4.  Проведення практичного заняття

Заняття проводиться з використанням інструкційних карт (додаток 2).

 

4.1. Підготовчий етап

1.              Перевірка  домашнього завдання за допомогою документ-камери (додаток 4) та відповіді на запитання, що виникли у студентів під час виконання домашнього завдання.
2.              Актуалізація опорних знань (додаток 5) .

4.2. Узагальнення та систематизація знань (додаток 2).  

4.3. Розв’язування задач (додаток 2). 

4.4. Виконання самостійної роботи (додаток 7).

 

5.   Завершальний етап:

         5.1. Підведення підсумків заняття.

         5.2. Оцінювання діяльності студентів на занятті.

Методичне обґрунтування проведення практичного заняття

 

 Сучасні роботодавці зацікавлені в такому працівнику, що не тільки добре володіє необхідним теоретичним матеріалом, уміє застосувати отримані знання на практиці, але здатен сам «добувати» знання, орієнтуватися в нестандартній ситуації, а також може працювати в колективі. Ці якості особливо коштовні щодо випускників економічних спеціальностей.

Застосування   комп’ютерних  програм для розв’язання математичних задач  сприяють  розвитку відповідальності,самостійності, акуратності.

На попередньому занятті студенти  розглянули як за допомогою похідної знаходять проміжки зростання та спадання функції, екстремуми функції, проміжки опуклості функції, точки перегину. Отримані знання допоможуть студентам закріпити навички дослідження та побудови графіків. На початку заняття  пропонується  повторити вивчений матеріал. 

За допомогою документ-камери на дошці з’являється зразок домашнього завдання. За правильну відповідь студенти виставляють 1бал в талон самоконтролю.

Наступним кроком перевірки засвоєних знань є запропонована таблиця, в якій треба встановити відповідність похідної та її графіку. Вірність заповнення таблиці студенти перевіряють самостійно за допомогою зображення заповненої таблиці на дошці.

Фронтальне опитування, також як виконання завдань в таблиці оцінюється в 1 бал. Результати заносяться в талон самоконтролю. Завдяки даним формам перевірки знань, студенти набувають навички  самостійності,  самоконтролю і самокорекції, займають активну позицію. Відповіді коментуються викладачем.

 Безпосередньо практична робота виконується згідно інструкційної карти. В ППП MathCAD студенти будують графік згідно вказаному алгоритму. Практична робота складається з трьох завдань.

Перше та друге завдання виконується колективно за допомогою викладача. В економіці часто користуються середніми величинами: обчислюють середню собівартість продукції, середню продуктивність  праці. Проте, при вивченні деяких процесів в економці зустрічають і такі задачі, де потрібно з’ясувати, на яку величину зростуть витрати виробництва, якщо збільшити  обсяг продукції, і, навпаки, наскільки зменшаться витрати виробництва, якщо скоротити обсяг продукції;  з’ясувати залежність попиту на товар від ціни на нього. Середні величини відповіді на такі  питання не дають.  Такі питання розв’язують задачі графічного характеру, а тому варто розглянути приклад. Наприкінці нашого заняття пропоную всім студентам виконати самостійну роботу.

 

 

 

 

ЛІТЕРАТУРА

 

1. Алгебра и начала анализа.Ч.1.Учебник для средних специальных учебных заведений.−/ Под ред. Яковлева Г.Н.,  М.: Наука, 1987. − 463с.
2.  Богомолов В.Н. Практические занятия по математике. − М.: Наука, 1982.-564с.
3. Колєсніков А.Н Краткий курс математики для экономистов.М.:

«ИНФРА-М», 1999. − 207с.

4. Кутепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функціям. М., 1974. −567с.
5. Сергиенко Л.Ю., Самойленко П. И. Планирование учебного процесса по математике: Учеб. − метод. пособие для преподавателей серед. спец. учеб. заведений. − М.: Высш. Шк., 1987. − 424 с.: ил.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

 

Талон самоконтролю

 

Прізвище, ім’я ____________________________________________________

Група___________________

 

1.	Домашнє завдання          (1б)
2.	Таблиця-тест                    (1б)
3.	Усна робота                     (1б)
4.	Самостійна робота          ( 2б)
5.	Всього

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2

Інструкційна карта

до практичного заняття

з дисципліни “Вища математика”

Тема: “ Диференціальне числення функції однієї змінної ”

Тема практичного заняття: “Дослідження функції за допомогою похідної і побудова її графіка”

Мета: Сформувати вміння та навички обстеження функції за допомогою диференціального числення та побудови її графіка.

Методичне забезпечення: інструкційна карта

Методичні вказівки: Загальна схема дослідження функції і побудова їх графіків.

   Для побудови графіку зручно користуватись схемою, в якій узагальнено матеріал даного розділу.

1.         Знайти область визначення функції.
2.         Визначити чи функція є парна, непарна та періодичність функції.
3.         Знайти точки перетину графіка функції з осями координат.
4.         Знайти проміжки монотонності і екстремуми функції.
5.         Знайти напрямки опуклості і точки перетину функції.
6.         Побудувати графік функції, використовуючи всі одержані результати досліджень.  Якщо їх виявилось недостатньо, то потрібно знайти ще декілька точок графіка функції, виходячи з її рівняння.

 

1. Актуалізація опорних знань.
   1.  Перевірка домашнього завдання за допомогою документ-камери

(додаток 4).

2. Заповнити таблицю, у клітках якої потрібно знаком «+» указати відповідність «функція – графік похідної цієї функції».

 

 

 

 

Графік   Функція похідна
у' =
у' =
у' =
у' =
у = 2х – 7 у' =
у = 2х + х4 у' =

 

3. Відповісти на контрольні запитання.

1. Сформулюйте умови зростання та спадання функції.
2. Сформулюйте необхідну умову існування екстремуму функції.
3. Сформулюйте достатні умови існування екстремуму функції.
4. Як знайти точку екстремуму функції?
5. Сформулюйте  необхідну умову опуклості кривої.
6. Сформулюйте достатню умову опуклості кривої.
7. Як знайти напрямки опуклості і точки перегину кривої?
8. Які види асимптот ви знаєте?
9. Як знайти похилу, вертикальну та горизонтальну асимптоти?

2. Порядок виконання практичної роботи

 

1.  Колективне розв’язування задачі.

За допомогою програми MathCAD дослідити та побудувати графік функції  .

1. Запустити програму MathCAD.
2. Послідовно відкрити вказані нижче вікна програми та виконати наступні дії.

 

 

 

 

 

 

 

 

 

 

 

 

                  

 

 

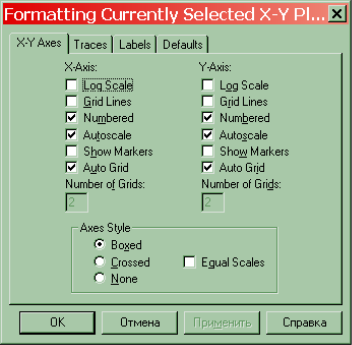
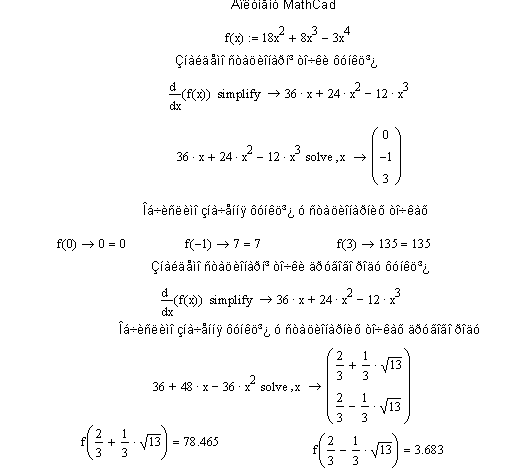
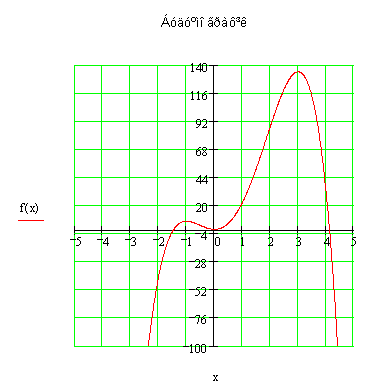
2.       Розв’язування економічної задачі

 

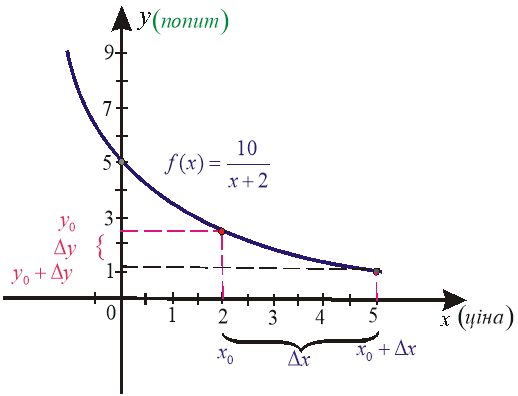
Нехай фірма планує збільшити ціну на товар. Необхідно дослідити, як при цьому зміниться попит на цей товар. Під попитом ми розуміємо обсяг суспільної потреби, яка виражається в грошах (іншими словами, попит – це кількість грошей, яки покупці спроможні заплатити за товар при певному рівні ціни на нього). При підвищенні ціни на товар зменшується попит, а при зниженні – збільшується. Отже, попит  на товар є функцією ціни  , де   − ціна, − попит. Відомо, що функція попиту для даного ринку має вигляд: . Ставиться задача: з якою швидкістю змінюється попит при зміні ціни за умови, що початкова його ціна становить 2 грн.

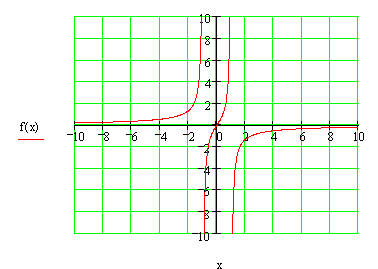
Графік функції має вигляд (додаток 6).

 

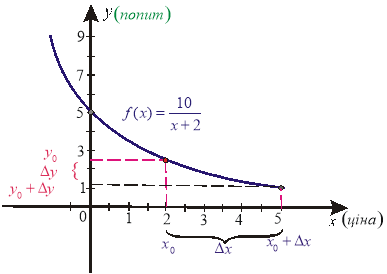
Оскільки залежність попиту від ціни продукції виражається функцією  , то при зміні ціни від    до попит змінюється від значення  до . Треба звернути увагу, що >0, оскільки попит зменшився. Отже,

.

Швидкість зміни попиту в момент ціни x₀ можна визначити як граничне значення відношення  при  , тобто визначити, як швидко зменшиться попит на товар при надзвичайно малому підвищені ціни, тобто миттєву швидкість зміни попиту.

 

 

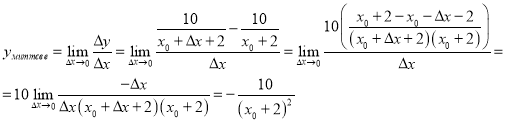
Функція      є похідною функції .

Для  , .

 

Отже, миттєве значення зниження попиту становить 0,625 одиниці.

 

Графік  побудований  у пакеті прикладних програм MathCAD.

 

 

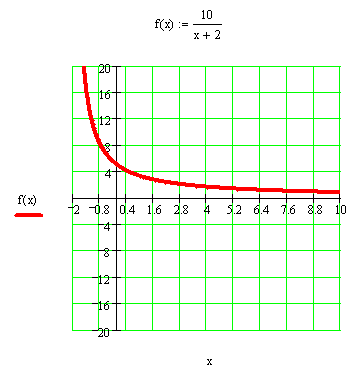
2.3. Самостійна робота студентів (додаток 6).

        

 

 

 

 

 

 

 

 

Зразок розв’язання самостійної роботи

 Дослідити та побудувати графік функції  . За допомогою пакета MathCAD зробити перевірку.

 

Розв’язання.

1. .

2.  функція непарна.

3.  .

4.   - вертикальні асимптоти.

    де   

                          

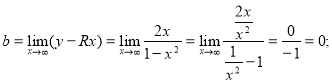
                           горизонтальна асимптота.

5.

      

Отже, критичних точок нема.

         >0

  >0

         >0

 

Функція зростає  при  .

 

6.

коли

  <0,  >0,  <0, >0.

 

 

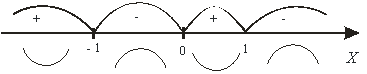
Графік функції повернутий опуклістю вниз на интервалі

і вгору  ;

  − точка перегину, 

 

                

 

  

3. Домашнє завдання  

Дослідити функцію та побудувати її графік     .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 3

Інтелектуальна картка

 

Тема:  “Дослідження функції та побудова її графіки”

 

Зростання та спадання  графіка функції

Якщо для x₁>x₂, де x₁, x₂ належать (a, b) виконується умова f(x₁)>f(x₂), то функція f(x) зростає на (a;b); якщо ж виконується умова f(x₁)<f(x₂), то функція f(x) спадає на (a; b).

Необхідна та достатня умова монотонності функції на проміжку

Якщо диференційована функція  y=f(x), x(a; b), зростає (спадає) на (a; b), то f'(x)0(f’(x)0)для будь-якого х з цього проміжку. Справедливе і обернене твердження: якщо f'(x)0 (f'(x)0) то функція зростає (спадає) на цьому проміжку.

Опуклість   та точки перегину кривої

На проміжку a<x<b графік функції є опуклий вгору, якщо він лежить нижче дотичної, яка проведена в будь-якій його точці.

На проміжку b<x<c графік функції є опуклий вниз, якщо він лежить вище дотичної, яка проведена в будь-якій точці.

\ Достатня умова опуклості кривої

Графік двічі диференційованої функції y=f(x) є опуклим вгору на проміжку f<x<b? якщо друга похідна функції від’ємна в кожній точці цього проміжку:                                                        f''(x)<0 для a<x<b.

Графік двічі диференційованої функції y=f(x) є опуклим вниз на проміжку b<x<c, якщо друга похідна функції додатня в кожній точці цього проміжку:                                                        f''(x)>0 для b<x<c.

Необхідна умова існування точки перегину

Якщо функція y=f(x) має неперервну похідну до другого порядку включно на інтервалі (a;b) і точка (x₀;f(x₀)) є точкою перегину графіку функції y=f(x), то f''(x)=0.

Достатня умова існування точки перегину

Нехай функція y=f(x) двічі диференційована на (a; b) і при переході через точку x₀ її друга похідна змінює знак. Тоді точка кривої з абсцисою x=x₀ є точкою перегину.

Точками підозрілими на перегини є точки, в яких друга похідна дорівнює нулю, або не існує. Такі точки називаються критичними точками ІІ роду.

 

 

Щоб знайти напрямки опуклості і критичні точки другого роду потрібно:

1.   Знайти область визначення функції.
2.   Знайти другу похідну функції і критичну точку другого роду.
3.   Відмітити границі області визначення і критичні точки другого роду на числовій прямій.
4.   Дослідити знак другої похідної в кожному із одержаних інтервалів.
5.   Встановити проміжки опуклості.
6.   Визначити абсцису точки перегину і обчислити її ординату.

Екстремум функції  

Необхідна умова існування екстремуму диференційованої функції (теорема Ферма): якщо f(x) в т. x=a має екстремум, то її похідна в цій точці рівна нулю, або не існує.

Достатньою умовою існування екстремуму в точці х=а  є зміна знаку похідної при переході через дану точку.

Схема дослідження функції

на екстремум за допомогою першої похідної

   Неважко виділити основні моменти дослідження функції на екстремум:

1. Встановити область визначення заданої функції f(x);

2. Визначити критичні точки функції.

          а) знайти похідну функції f(x);

          б) встановити, при яких значеннях аргументу y'=0 або y' не існує.

3. Встановити проміжки монотонності:

          а) розбити область визначення функції критичними точками на проміжки;

          б) встановити знак похідної на кожному проміжку;

          в) зробити висновок про характер монотонності функції на кожному з проміжків.

4. Визначити екстремальні точки.

Загальна схема дослідження функції і побудова їх графіків

   Для побудови графіку зручно користуватись схемою, в якій узагальнено матеріал даного розділу.

1. Знайти область визначення функції.
2. Визначити чи функція є парна, непарна та періодичність функції.
3. Знайти точки перетину графіка функції з осями координат.
4. Знайти проміжки монотонності і екстремуми функції.
5. Знайти напрямки опуклості і точки перетину функції.
6. Побудувати графік функції, використовуючи всі одержані результати досліджень.  Якщо їх виявилось недостатньо, то потрібно знайти ще декілька точок графіка функції, виходячи з її рівняння.

 

Додаток  4

 

Зразок домашнього завдання

№ 1.  Дослідити функцію на монотонність, екстремум, опуклість та знайти точки перегину.

Розв’язання.

Область визначення є множина всіх дійсних чисел.

Знайдемо стаціонарні точки функції: ,  . Відмітимо критичні точки  першого роду на числовій прямій і досліджуємо знак похідної в кожному із одержаних проміжків:

                                     

   

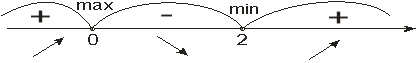                             x

Функція зростає при , спадає при  ;

−точка максимуму,   − точка мінімуму, .

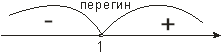
За допомогою другої похідної знаходимо напрямки опуклості і точки перегину графіка функції: , - критична точка другого роду, . Досліджуєм знаки другої похідної:

                                       

 x

Графік функції повернутий опуклістю вниз на интервалі; і вгору ;

− точка перегину,  .

 

№ 2.  Знайти найбільше та найменше значення функції на відрізку:

                                          

 Розв’язання.

Знайдемо похідну функції і критичні точки першого роду з умови  .

                                             

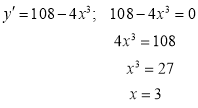
Знайдемо значення функції на кінцях відрізку та у  критичних точках:

                                 ;       

 таким чином,

                            .

Додаток 5

Таблиця тест для перевірки знань

 

У комірках таблиці-тесту  потрібно знаком «+» указати відповідність «функція – графік похідної цієї функції».

 

Графік     Функція похідна
у' = 2 – 3х2	+
у' = х2 + 2			+
у' = х		+
у' = 2 - х				+
у = 2х – 7 у' = 2						+
у = 2х + х4 у' = 2 + 4х3					+

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 6

 

Графік швидкості змінення попиту при зміні ціни

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 7

Завдання щодо проведення самостійної  роботи студентів

  

Дослідити функцію та побудувати графік функції

 

1. .                                                  2. .

3. .                                                 4. .

5. .                                                6. .

7.                                                   8. .

9. .                                                10. .

11. .                                            12. .

13.                                           14. . 

15. .                                             16. .

 17. .                                             18.   

19. .                                            20. .                                                                               

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 8

Критерії оцінки знань студентів

 

При виставленні оцінки студенту враховується :

 

1) правильність виконання домашнього завдання;

2) правильність виконання завдань із таблиці-тесту;

3) грамотність відповідей на теоретичні питання;

4) самостійність роботи;

6) уміння застосувати знання в нестандартній ситуації.

 

Знання студентів оцінюються з урахуванням самостійної оцінки студентів за домашнє завдання, тесту та усних відповідей, а також оцінки за самостійну роботу, яку оцінює викладач.

 

Оцінка «відмінно» виставляється якщо студент:

 

•         Відмінно виконав домашнє завдання;
•         Правильно вказав зв’язки між похідною і її графіком.
•         дає повні, правильні і логічні усні відповіді;
•         повною мірою володіє  методикою дослідження функції;
•         відмінно виконав самостійну роботу.

 

 Оцінка «добре» виставляється якщо студент:

 

•         не допускав істотних неточностей у відповідях і при розв’язанні завдань.
•         добре або відмінно виконав самостійну роботу.
•         не досить активно брав участь у  колективній роботі та фронтальному опитуванні.

 

 Оцінка «задовільно» виставляється якщо студент:

 

•         пасивно брав участь у проведенні  практичного заняття та окремих його частин;
•         добре або задовільно виконав самостійну роботу;
•         добре володіє теоретичними знаннями;
•         непевно застосовує схему дослідження функції.

 

 Оцінка «незадовільно» виставляється якщо студент:

 

•         не брав участь у проведенні  практичного заняття;
•         давав неправильні відповіді на теоретичні питання;
•         не володіє методикою рішення жодного з типів диференціальних рівнянь;
•         одержав незадовільну оцінку за самостійну роботу.