Методична розробка на тему: «Методика розв’язування задач з геометрії»

Вище професійне училище № 25 смт Демидівка

Методична розробка

 на тему:

 «Методика розв’язування

задач

з геометрії»

Підготувала

викладач математики

спеціаліст першої категорії

Волошин Світлана Володимирівна

2019 р

Методика розв’язування задач з геометрії

Пам’ятайте: якщо ви хочете навчитися плавати, то сміливо заходьте у воду, а якщо хочете навчитися розв’язувати задачі, то розв’язуйте їх!

Д. Пойа

Основним засобом навчання математики є задачі. Вони виконують навчальну, розвивальну, виховну та контролюючу функції.

При розв’язуванні конкретної задачі у якості головного для вчителя виступає провідна функція, заради якої розв’язувалась задача:

- навчальна функція задач спрямована на формування в учнів систем математичних знань, умінь і навичок на різних етапах їх засвоєння;

- виховна функція задач визначається цілями виховання і спрямована на виховання пізнавального інтересу, самостійності у здобутті знань і навичок навчальної праці, моральних якостей, культури;

- розвивальна функція задач спрямована на розвиток мислення учнів, на їх навчання ефективним прийомам розумової діяльності, наприклад, навчання вмінню виділяти головне, суттєве в задачах та їх розв’язуванні;

- контролююча функція спрямована на встановлення рівня навченості, математичного розвитку учнів, здібностей до самостійного вивчення математики, сформованості пізнавальних інтересів учнів тощо.

Для формування умінь розв’язувати задачі з геометрії необхідно навчати учнів спеціальним знанням про задачі та їх розв’язування. Без них ці уміння формуються стихійно і можуть виникнути лиш при розв’язуванні великої кількості задач. Багато учителів на розв’язування задач відводять більше половини навчального часу, але результати такої роботи не завжди значні.

Під час розв’язування задачі учитель, як правило, основну увагу приділяє пошуку розв’язання та його запису. Це, без сумніву, правильно. Однак, як свідчить практика, на висновки після знайденого розв’язання задачі часто не залишається ні сил, ні часу. Технічна сторона розв’язування часто закриває більш важливу – навчально-пізнавальну ціль, те головне, для чого розв’язувалась задача. Важливо збагатити учнів загальними методами розв’язування задач, бо не кількість розв’язаних задач, а метод їх розв’язання визначає навчальний ефект.

Важливими умовами, що визначають вибір основного, суттєвого під час розв’язування задач, ми вважаємо формування в учнів загального підходу до розв’язування будь-яких задач і засвоєння знань, необхідних для цього. Такими є знання:

•       про структуру задачі та структуру розв’язування задачі;
•       про основні типи задач;
•       про етапи їх розв’язування;
•       про основні методи розв’язування задач;
•       про ознаки застосування методів.

Учителю слід ознайомити учнів із загальною структурою розв’язування задачі. Цей процес можна розділити на 8 етапів. Його структуру можна зобразити такою схемою:

Головним в умові задачі є математичні залежності між даними, між даними і шуканими величинами та теоретичні відомості, що відображені в умові, чи слідують із розв’язування. Так у підручнику з геометрії                     О. В. Погорєлова до задач віднесено багато теорем, які часто застосовуються під час розв’язування задач. Це, наприклад:

• задача про властивість бісектриси трикутника;
• задача про властивість відрізка дотичних, проведених до кола з однієї точки;
• задачі про властивості паралелограма;
• задачі про властивості вписаного і описаного чотирикутників;
• окремі формули площі трикутника, чотирикутників та ін.

Тому і вчитель, і учні завжди мають знати, для чого вони розв’язують ту чи іншу задачу, розуміти, що із розв’язування слід виділяти такі знання та уміння, які важливі для подальшого навчання.

Учителю треба вчити учнів шукати способи розв’язування задач. Основними методами пошуку розв’язування є аналітичний та синтетичний. Нагадаємо, що аналітичний – це метод міркувань від невідомих, шуканих до даних величин. Синтез – це метод міркувань від даних до шуканих, невідомих величин. Синтетичний метод доцільно використовувати тоді, коли задача легка або вже відомий спосіб її розв’язування. Йому треба надавати перевагу в молодших класах. Спосіб розв’язування більшості задач, зокрема складніших, треба шукати аналітичним методом, виходячи з вимоги задачі. Тоді кожний крок учня цілеспрямований, він шукає тільки те, що треба знайти, а не те, що можна (як при синтетичному методі). Звичайно, і при розв’язуванні аналітичним іноді доводиться вдаватися до синтезу. Коли розв’язують важку задачу, то користуються аналітико-синтетичним методом: прокладають шлях і від вимоги, і від умови, поки не буде знайдено зв’язку між ними. Здійснювати пошук розв’язування задачі аналітико-синтетичним методом учителю слід у формі евристичної бесіди, продумавши систему цілеспрямованих запитань до учнів.

Учнів треба вчити розв’язувати задачі окремих типів. Якщо встановлений тип задачі, то зроблений важливий крок у пошуку плану її розв’язування. Розпізнавання типу задачі вимагає від учнів уміння виділяти головне в умові задачі, бо тип задачі визначається характером її вимоги або основними співвідношеннями між даними й шуканими величинами.

За характером вимоги розрізняють чотири основних види задач:

• задачі на обчислення;
• задачі на доведення;
• задачі на дослідження;
• задачі на побудову.

Більшість конкретних типів задач шкільного курсу математики мають алгоритмічний або напівевристичний характер. Існують алгоритми розв’язування різних типів рівнянь, нерівностей, задач на рух, на спільну роботу, на відсотки тощо. Тому при розв’язуванні стандартних задач, тобто задач, що мають певний алгоритм розв’язування, важливим є навчання учнів складати і застосовувати алгоритми та схеми розв’язування. Наприклад, при розв’язуванні геометричних задач на обчислення можна використати такий алгоритм:

1. зробити схематичний малюнок;
2. позначити одну з невідомих величин через х;
3. виразити через х невідомі величини;
4. записати і розв’язати рівняння;
5. записати і перевірити відповідь.

Розв’яжемо для прикладу задачу, яку можна запропонувати учням І–го курсу на уроці геометрії, і разом з тим пригадати вивчений шкільний матеріал.

ЗАДАЧА 1

Периметр ромба дорівнює 20 см, а сума його діагоналей – 14 см. Знайти площу ромба.

Розв’язання

.

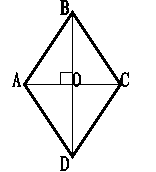
Нехай .

Тоді ;

.

Оскільки діагоналі ромба взаємно перпендикулярні:

то .

За умовою см, отже см.

Тоді ; ; , .

Значить см, см (або см, см).

Отже, площа ромба обчислюється см.

Відповідь: 24 см.

На прикладі розв’язування задачі-моделі певного типу, доцільно виділяти основну ідею, суттєві сторони способу розв’язування, а потім застосовувати його до окремих задач. Тоді дією і прямим результатом дій учнів буде спосіб розв’язування, а розв’язування окремих задач – побічним результатом навчання.

Учнів доцільно ознайомити з ознаками, за якими можна встановити, яким із основних методів – алгебраїчним (метричним), координатним, векторним, методом геометричних перетворень – краще всього розв’язувати геометричну задачу.

Розглянемо, за якими ознаками можна співвіднести задачі із певним методом розв’язування.

 Види геометричних задач, які можна розв’язувати координатним методом:

1. Задачі на відшукання геометричних місць точок (ГМТ).
2. Задачі на доведення залежностей між лінійними елементами геометричних фігур.

Розв’язуючи задачу координатним методом виконують три кроки:

1. записуємо геометричну задачу мовою координат;
2. перетворюємо алгебраїчний вираз;
3. переводимо знайдений результат на мову геометрії.

Розглянемо задачу.

ЗАДАЧА 2

Довести, що сума квадратів діагоналей трапеції дорівнює сумі квадратів бічних сторін, доданій до подвоєного добутку основ.

Розв’язання

Зобразимо трапецію у системі координат, як на рисунку.

Вершини трапеції мають координати:

А(0;0), В(с;d), C(a;b), D(d;0).

Тоді:       (1).

             (2).

З рівностей (1) і (2) маємо:

, що й треба було довести.

Відповідь: задачу доведено.

Види геометричних задач, які можна розв’язувати векторним методом:

1. Задачі, пов’язані з доведенням паралельності прямих;
2. Задачі, в яких треба довести, що деяка точка ділить відрізок у певному відношенні, зокрема, є його серединою;
3. Задачі, в яких треба довести, що три точки А, В, С лежать на одній прямій;
4. Задачі, в яких треба довести, що даний чотирикутник АВСD – паралелограм;
5. Задачі на знаходження довжини відрізка;
6. Задачі на знаходження величини кута;
7. Задачі, в яких лінійні елементи та кути розміщенні в різних площинах і звести їх в одну площину неможливо або недоцільно та ін.

Алгоритм застосування векторного методу до розв’язування задачі такий:

1) сформулювати задачу на мові векторів. Для цього спочатку слід розглянути деякі з даних у задачі відрізків як вектори і записати векторну рівність;

2) перетворити векторну рівність, користуючись законами дій над векторами, відомими векторними рівностями;

3) перекласти знайдений результат на мову геометрії.

Розв’яжемо векторним методом задачу.

ЗАДАЧА 3

Довести, що середини сторін чотирикутника є вершинами паралелограма.

Розв’язання

Нехай E, F, M, N – середини сторін чотирикутника ABCD. Достатньо довести, що . Якщо О – довільна точка площини, то:

       ,   ,       ,  .

,  .        

Значить, , що й треба було довести.

Відповідь: задачу доведено.

Види геометричних задач, які можна розв’язувати методом геометричних перетворень:

Щоб розв’язати задачу методом геометричних перетворень треба:

1) розглянути поряд з даними фігурами нові фігури, які дістали з даних за допомогою певного перетворення (симетрії, повороту чи паралельного перенесення);

2) з’ясувати властивості нових фігур;

3) перенести ці властивості на дані фігури.

Розглянемо приклад розв’язування задачі.

ЗАДАЧА 4

Дано гострий кут АВС і точку М у середині його. Побудувати на сторонах кута такі точки Х  і Y, щоб ∆МХY мав найменший периметр.

Розв’язання

Аналіз. Припустимо, що ∆МХ₁Y₁ – шуканий. Одна вершина трикутника відома – точка М. Точки Х₁ і Y₁ – треба знайти. Встановимо, які умови задовольняють ці точки.

Перша: Х₁ і Y₁ лежать відповідно на сторонах ВА і ВС кута АВС. Для знаходження другої умови будуємо точки М₁ і М₂ симетричні відносно сторін кута. Будуємо відрізки МХ₁, МY₁, М₁М₂. Периметр трикутника дорівнює сумі МХ₁+ Х₁Y₁+МY₁. Він має бути найменшим. Довжина ламаної М₁Х₁Y₁М₂ буде найменшою тоді, коли точки М₁, Х₁, Y₁, М₂ лежатимуть на прямій М₁М₂. Отже, шукані точки Х₁ і Y₁ є точками перетину сторін кута ВА і ВС з прямою М₁М₂.

Побудова. Будуємо:

1) точки М₁ і М₂, симетричні точці М відносно сторін даного кута;

2) пряму М₁М₂;

3) точки Х  і Y перетині прямої М₁М₂ із сторонами ВА і ВС кута.

∆МХY – шуканий.

Відповідь: задачу виконано.

Потрібно учнів вчити розуміти, яким методом краще і зручніше розв’язувати геометричну задачу. Для прикладу розглянемо задачу на обчислення, яку можна розв’язати 3-ма методами: геометричним, алгебраїчним і тригонометричним.

ЗАДАЧА 5

В рівнобедреному трикутнику основа дорівнює 12см., а бічна сторона 10см. Знайти висоту, проведену до бічної сторони?

Розв’язання

1. Геометричний метод.

Використаємо геометричну властивість – теорему Піфагора.

 Із подібності трикутників випливає відношення .

Звідси маємо, що

2. Алгебраїчний метод.

Нехай . Тоді з ∆ALB маємо, що AL²=AB²-BL².

Аналогічно з трикутника ∆ALС маємо, що AL²=AС²-СL².

Звідси, AB²-BL²=AС²-СL², тобто 10²-(10-х)²=12²-х².

100-100+20х-х²=144-х²,

20х=144,

х=7,2 , тобто . Звідси

3. Тригонометричний  метод.

З ∆ALC маємо, що . Отже AL=AC∙sinC=12∙0,8=9,6 .

Відповідь: 9,6 см.

Уміння учнів розв’язувати математичні задачі суттєво залежать від організаційних прийомів і способів навчання, які використовує у своїй роботі вчитель. Найчастіше використовують колективне (фронтальне)  та індивідуальне розв’язування задач.

Колективне розв’язування задач – це розв’язування однієї і тієї ж задачі всіма учнями групи в один і той самий час. Організація колективного розв’язування задач може бути різною.

Письмове розв’язування задач із записом на класній дощці найчастіше застосовують у таких випадках:

а) при розв’язуванні перших після показу вчителем задач, спрямованих на закріплення нових понять, теорем, методів розв’язування тощо;

б) при розв’язуванні задач, самостійно з якими можуть справитися не всі учні групи;

в) при розгляді різних способів розв’язування однієї і тієї ж задачі, для порівняння і вибору раціональнішого;

г) для аналізу помилок, що їх допустили деякі учні групи, розв’язуючи задачу самостійно тощо.

Як показують спостереження, під час колективного розв’язування задач із записом на дошці частина учнів розв’язують задачі в своїх зошитах самостійно, звіряючи свої відповіді з тими, що на дошці, а частина списує з дошки. У цьому цінність такої роботи, бо ті учні, які не зрозуміли пояснення вчителя або забули попередній матеріал, списуючи з дошки, вчаться розв’язувати задачі. Але в цьому і недолік такої роботи, бо завжди є такі учні, які при цьому вчаться тільки списувати. Тому час від часу треба пропонувати задачі для самостійного розв’язування.

Ефективним є письмове самостійне розв’язування учнями задач.

По-перше, воно розвиває розумові здібності, підвищує навчальну активність учнів, пробуджує в них інтерес до розв’язування задач, стимулює творчу ініціативу. Таким чином, підвищується ефективність уроку.

По-друге, не маючи можливості переписувати розв’язання задачі з дошки, учень змушений самостійно шукати його, краще готуватися до уроків з математики.

По-третє, дає можливість скоротити час, необхідний для перевірки знань і умінь учнів.

По-четверте, вчитель отримує можливість спрямувати індивідуальну роботу учнів, попереджувати і виявляти помилки, вказувати шляхи їх виправлення.

Учителю треба заздалегідь визначити цілі самостійного розв’язування учнями задач:

• Формування нових знань і вмінь;
• Закріплення і застосування вивченого матеріалу;
• Перевірка рівня знань і вмінь учнів тощо.

Під час навчальних самостійних робіт учитель має допомагати учням порадами, підказками. Учням, які розв’язали задачу швидше від інших, учитель може запропонувати іншу задачу, або просить допомогти сусідові, або пропонує помінятися зошитами з іншим учнем, який також розв’язав задачу, для взаємної перевірки розв’язання тощо.

Перед початком письмового самостійного розв’язання учнями задач учителю потрібно провести інструктаж стосовно змісту, форми і часу виконання. Після перевірки правильності самостійних розв’язань доцільно проаналізувати з учнями отримані результати.

Коментоване розв’язування задач полягає в тому, що всі учні самостійно розв’язують одну і ту ж задачу в зошиті, а один із них послідовно пояснює (коментує) розв’язання. Кожний учень має уважно слухати пояснення, бо учитель у будь-який момент може запропонувати продовжити пояснювати розв’язання йому. При коментованому розв’язуванні задачі головним є не швидкість розв’язання, а його обгрунтування. Коментованому розв’язанню задач або самостійній роботі має передувати колективне розв’язування учнями задач із записом на дошці.

 Під час вивчення всіх без винятку розділів математики є можливість і потреба розв’язувати задачі усно. Доцільно не тільки планувати спеціальні «п’ятихвилинки» усного розв’язування задач, а й використовувати його під час письмового розв’язування. Способи усного розв’язування задач учні мають шукати як самостійно, так і за допомогою вчителя.

Вправи, які легко розв’язати усно, але важко запам’ятати, треба записувати на дошці або проектувати за допомогою діапроектора. Ефективним є усне розв’язування геометричних вправ за готовими малюнками. Їх можна використовувати при фронтальному опитуванні і перевірці домашнього завдання, перед поясненням нового матеріалу чи після нього, під час повторення і закріплення тощо. Розв’язуючи задачі усно, вчителю потрібно максимально стимулювати мислення учнів, вчити їх критично ставитись до формулювання та обґрунтування своїх відповідей.

Розглянемо для прикладу кілька усних задач. При вивчені на І-му курсі теми «Перпендикуляр і похила» для розвитку просторової уяви актуальною є така малюнок-задача.

ЗАДАЧА 6

Радіощогла висотою 30м кріпиться трьома тросами на висоті 16м від землі. Місця кріплення знаходяться на відстані 12м від основи щогли. Знайти довжину тросів?

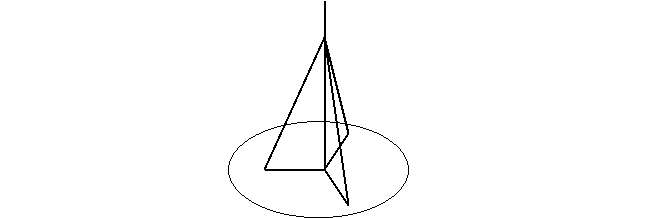
Розв’язання

Зрозуміло, що тут дані три рівні прямокутні трикутники з відомими катетами. Треба знайти гіпотенузу, що є довжиною тросів. Отже м.

Відповідь: задачу розв’язано.

Під час вивчення теми «Декартові координати» варто перевірити вміння учнів розв’язувати усні задачі, які також допомагають розвивати логічне мислення.

ЗАДАЧА 7

Яка з точок А(5; -6; 8), В(-2; 0; 11), С(-7; 3; 8) найближча до початку координат?

Розв’язання

Зрозуміло, що такою точкою буде точка  В(-2; 0; 11), бо вона вже має одну координату, що рівна 0.

Відповідь: задачу розв’язано.

ЗАДАЧА 8

Доведіть, що трикутник з координатами вершин (-5; 0; 0), (0; -5; 0) і         (0; 0; -5) – рівносторонній.

Розв’язання

Вершини цього трикутника лежать на координатних осях, довжини сторін якого рівні по 5 одиниць. Отже трикутник рівносторонній.

Відповідь: задачу розв’язано.

Колективне розв’язування задач не завжди приводить до бажаних результатів у навчанні математики. Для одних учнів задача може виявитись досить легкою, а для інших навпаки, викличе помітні труднощі. Завдання вчителя полягає в тому, щоб визначити рівень навчальних досягнень, можливостей і здібностей кожного учня до вивчення математики і у відповідності до цього організувати індивідуальне розв’язування задач.

Учителю потрібно пропонувати для самостійного розв’язування не однакові, а різні задачі, добираючи їх для груп учнів з приблизно однаковим рівнем навчальних досягнень з математики: низьким (рецептивно-продуктивним), середнім (репродуктивним), достатнім (конструктивно-варіативним), високим (творчим). З цією метою на уроках доцільно використовувати диференційовані дидактичні матеріали. При такій організації навчання «слабші» учні, розв’язавши задачу самостійно або з допомогою вчителя, набувають віри у свої сили, а «сильніші» учні мають можливість розвивати свої здібності.

Оскільки учні мають різну підготовку з геометрії, а в цілому з математики, слід індивідуалізувати домашні завдання. За допомогою індивідуальних домашніх завдань (паралельно з роботою на уроці) можна виявити нахили окремих учнів, виховувати в них захоплення математикою.

Насамкінець, підкреслю, що уміння розв’язувати задачі є мистецтво, яке здобувається практикою. Щоб задачі були засобом формування особистості учня, після розв’язування кожної з них слід поставити запитання: «Для чого розв’язувалась дана задача? Чому ми навчились при її розв’язуванні? Що головне потрібно взяти із задачі для подальшої роботи?» Як вважають психологи, цей етап роботи із уже розв’язаною задачею найцінніший для розумового розвитку учнів.