Пакет контрольних робіт з дисципліни "Математика"
Укладач: Вдовиченко Олена Володимирівна – викладач математики коледжу Подільського ДАТУ, спеціаліст І категорії.
Рецензент: Зваричук Валентина Іванівна – викладач математики коледжу Подільського ДАТУ, спеціаліст вищої категорії.
Пакет контрольних робіт призначений для поточного тематичного контролю рівня засвоєння студентами знань, сформованості умінь і навичок, передбачених програмними вимогами.
Запропоновано 13 тем, кожна з яких містить по 4 варіанти завдань, які охоплюють весь матеріал програми з дисципліни «Математика». Пакет контрольних робіт призначений для студентів спеціальності № 5.09010103 “Виробництво і переробка продукції рослинництва ”.
Рекомендовано цикловою комісією фізико-математичних дисциплін
Протокол №____________ від “_____”_______________2015 р.
ЗМІСТ
Вступ……………………………………………………….....................................4
Тема 1. Функції, їх властивості і графіки………………………………………..5
Тема 2. Степенева, показникова і логарифмічна функції ……………………...7
Тема 3. Тригонометричні функції……………………………..............................9
Тема 4. Рівняння, нерівності та їх системи…………….....................................11
Тема 5. Похідна та її застосування ……………….............................................13
Тема 6. Інтеграл та його застосування…………………....................................15
Тема 7. Систематизація та узагальнення фактів і методів планіметрії ……...17
Тема 8. Вектори і координати ………………………………….........................19
Тема 9. Паралельність прямих і площин у просторі…………..........................21
Тема 10. Перпендикулярність прямих і площин у просторі …………………23
Тема 11. Многогранники. Об’єми та площі поверхонь многогранників ……25
Тема 12. Тіла обертання. Об’єми та площі тіл обертання ………………........27
Тема 13. Елементи теорії ймовірностей та математичної статистики……….29
Список використаних джерел…………………………………………………..31
ВСТУП
Запропонований пакет контрольних робіт з дисципліни «Математика» створений з метою проведення тематичного контролю знань студентів І-ІІ курсів за спеціальністю № 5.09010103 "Виробництво і переробка продукції рослинництва".
Оцінювання навчальних досягнень учнів – невід’ємна і важлива складова навчального процесу. Оцінка, як кількісне вираження результату оцінювання, кваліфікує виконану учнем роботу, рівень його досягнень, сприяє усвідомленню ним помилок, формує почуття відповідальності, породжує бажання краще вчитися, стимулює до подальшої роботи.
Контроль знань студентів є важливим елементом наукової організації педагогічної праці. Системний, масовий і об’єктивний контроль рівня застосування студентами знань значно сприяє підвищенню ефективності та якості підготовки майбутніх спеціалістів.
Складені завдання охоплюють основні питання усіх тем дисципліни «Математика». Такі завдання спрямовані на перевірку ступеню засвоєння студентами навчального матеріалу. Запропоновані завдання відповідають чинній навчальній і робочій програмі.
На вивчення дисципліни «Математика» за навчальним планом передбачено 280 годин, у тому числі аудиторних 238 годин, самостійного вивчення 42 години.
Для кожної із 13 тем розроблено по 4 варіанти контрольної роботи. Кожний варіант містить завдання різних рівнів складності, які охоплюють весь матеріал по даній темі. Виконання тематичної контрольної роботи розраховано на 45 хв.
Всі варіанти контрольних робіт розглянуто і схвалено цикловою комісією фізико-математичних дисциплін.
Контрольна робота №1
« Функції, їх властивості і графіки»
Варіант 1
- Обчисліть абсолютну та відносну похибки чисел: (1бал)
![]() ,
, ![]()
- Знайдіть область визначення функції: (4бали)
а) ![]() б)
б) ![]() = 3
= 3![]() 2 –
2 – ![]() + 1
+ 1
в)![]() =
=![]() г)
г) ![]()
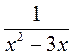
-
Розв’язати рівняння: (
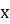 - 3)2 - (
- 3)2 - (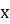 + 1)2 =12 (2бали)
+ 1)2 =12 (2бали)
- Дослідіть на парність функцію: (3бали)
![]() б)
б) ![]() в)
в) ![]()
- Знайдіть множину розв’язків нерівності: (2бали)
![]()
Варіант 2
- Обчисліть абсолютну та відносну похибки чисел: (1бал)
А = 200000, а = 199996
- Знайдіть область визначення функції: (4бали)
а) ![]() б)
б)![]()
![]() г)
г) ![]()
- Розв’язати рівняння: 25у2 – 4=0 (2бали)
- Дослідіть на парність функцію: (3бали)
![]() б)
б) ![]() в)
в) ![]()
- Знайдіть множину розв’язків нерівності: (2бали)
![]()
Варіант 3
- Обчисліть абсолютну та відносну похибки чисел: (1бал)
![]() ,
, ![]()
- Знайдіть область визначення функції: (4бали)
а) ![]() б)
б) ![]() = 3
= 3![]() 2 –
2 – ![]() + 5
+ 5
в)![]() =
= ![]() г)
г) ![]()
![]()
-
Розв’язати рівняння: (
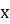 - 4)2 - (
- 4)2 - (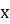 + 2)2 =14 (2бали)
+ 2)2 =14 (2бали)
- Дослідіть на парність функцію: (3бали)
![]() б)
б) ![]() в)
в) ![]()
- Знайдіть множину розв’язків нерівності: (2бали)
![]()
Варіант 4
- Обчисліть абсолютну та відносну похибки чисел: (1бал)
А = 300000, а = 299994
- Знайдіть область визначення функції: (4бали)
а) ![]() б)
б)![]()
![]() г)
г) ![]()
- Розв’язати рівняння: 36у2 – 9=0 (2бали)
- Дослідіть на парність функцію: (3бали)
![]() б)
б) ![]() в)
в) ![]()
- Знайдіть множину розв’язків нерівності: (2бали)
![]()
Контрольна робота №2
« Степенева, показникова і логарифмічна функції»
Варіант 1
- Знайдіть значення виразу: (2бали)
![]() б)
б)![]()
- Розв’яжіть рівняння: (3бали)
а)![]() б)
б)![]()
- Знайдіть корені рівняння: (4бали)
![]() б)
б)![]() 2-х+1)=0
2-х+1)=0
в) ![]() г)
г)![]()
- Розв’яжіть рівняння: (3бали)
а) ![]() б) 34х+1=81 в) 22х=512
б) 34х+1=81 в) 22х=512
Варіант 2
- Знайдіть значення виразу: (2бали)
![]() б)
б) ![]()
- Розв’яжіть рівняння: (3бали)
а) ![]() б)
б) ![]()
- Знайдіть корені рівняння: (4бали)
![]() б)
б)![]() 2+4х+3)=3
2+4х+3)=3
в) ![]() г)
г)![]()
- Розв’яжіть рівняння: (3бали)
а) ![]() б) 22х-1=32 в) 32х=729
б) 22х-1=32 в) 32х=729
Варіант 3
1. Знайдіть значення виразу: (2бали)
![]() б)
б) ![]()
- Розв’яжіть рівняння: (3бали)
а)![]() б)
б)![]() 3
3
- Знайдіть корені рівняння: (4бали)
![]() б)log3 х – 2
б)log3 х – 2![]() х = 3
х = 3![]()
в) ![]() г)
г)![]()
- Розв’яжіть рівняння: (3бали)
а) ![]() б) 34х+1=27 в) 22х=256
б) 34х+1=27 в) 22х=256
Варіант 4
1. Знайдіть значення виразу: (2бали)
![]() б)
б) ![]()
- Розв’яжіть рівняння: (3бали)
а) ![]() б)
б)![]()
- Знайдіть корені рівняння: (4бали)
![]() б)
б)![]() log4 х – 3
log4 х – 3![]() х = 8
х = 8![]()
в) ![]() г)
г)![]()
- Розв’яжіть рівняння: (3бали)
а) ![]() б) 22х-1=64 в) 32х=2187
б) 22х-1=64 в) 32х=2187
Контрольна робота №3
« Тригонометричні функції»
Варіант 1
- Спростіть вираз: (2бали)
![]() б)
б) ![]()
-
Доведіть тотожність:
 (3бали)
(3бали)
![]()
- Обчисліть: (2бали)
а) соs 240° б) tg 105°
- Знайдіть значення виразів: (3бали)
а) соs 32° соs 13° – sіn 32°sіn 13°
б) sіn 12° соs 18° + соs 12° sіn 18°
в) 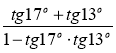
5. Обчисліть: (2бали)
а) соs 75° + соs 15° б) sin 150° + sin 30°
Варіант 2
- Спростіть вираз: (2бали)
![]() б)
б) ![]()
- Доведіть тотожність: (3бали)
![]()
- Обчисліть: (2бали)
а) sіn 240° б) tg 135°
- Знайдіть значення виразів: (3бали)
а) соs 156° соs 24° – sіn 156° sіn 24°
б) sіn 37° соs 53° + соs 37° sіn 53°
в) 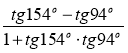
5. Обчисліть: (2бали)
а) sin 75° – sin 15° б) соs 150° + соs 30°
Варіант 3
- Спростіть вираз: (2бали)
![]() sіn
sіn![]() б)
б) ![]()
-
Доведіть тотожність:
 (3бали)
(3бали)
1+![]()
- Обчисліть: (2бали)
а) соs 150° б) tg 210°
- Знайдіть значення виразів: (3бали)
а) sіn 68° соs 8° – sіn 8° соs 6°
б) sіn 54° sіn 24°– соs 66° соs 126°
в) 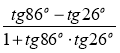
5. Обчисліть: (2бали)
а) соs 22° – соs 38°; б) sin 5° + sin 55°.
Варіант 4
- Спростіть вираз: (2бали)
![]()
![]() б)
б)![]()
- Доведіть тотожність: (3бали)
1 – ![]()
- Обчисліть: (2бали)
а) sіn 150° б) tg 120°
- Знайдіть значення виразів: (3бали)
а) соs 10° соs 35° – sіn 10° sіn 35°
б) соs 21° соs 24° + соs 69° соs 66°
в) 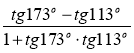
5. Обчисліть: (2бали)
а) sin 140° – sin 80° б) соs 130° + соs 50°
Контрольна робота №4
« Рівняння, нерівності та їх системи»
Варіант 1
- Розв’яжіть рівняння: (3бали)
а)![]() б)
б) ![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
- Розв’яжіть систему рівнянь методом підстановки: (4бали)
а)![]() б)
б)![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
-
Розв’яжіть систему нерівностей: (1бал)
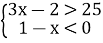
Варіант 2
- Розв’яжіть рівняння: (3бали)
![]() б)
б) ![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
- Розв’яжіть систему рівнянь методом підстановки: (4бали)
а)![]() б)
б)![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
-
Розв’яжіть систему нерівностей: (1бал)
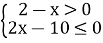
Варіант 3
- Розв’яжіть рівняння: (3бали)
а)![]() б)
б) ![]() .
.
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
- Розв’яжіть систему рівнянь методом підстановки: (4бали)
а)![]() б)
б)![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
-
Розв’яжіть систему нерівностей: (1бал)
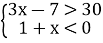
Варіант 4
- Розв’яжіть рівняння: (3бали)
![]() б)
б) ![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
- Розв’яжіть систему рівнянь методом підстановки: (4бали)
а)![]() б)
б)![]()
- Розв’яжіть нерівність методом інтервалів: (2бали)
![]()
-
Розв’яжіть систему нерівностей: (1бал)
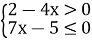
Контрольна робота №5
«Похідна та її застосування»
Варіант 1
- Знайдіть похідну функції: (6балів)
а) ![]() г)
г) ![]()
![]() д)
д)![]()
![]() = (7х
= (7х ![]() 6)52 е)
6)52 е)![]()
- Знайдіть екстремуми функції: (3бали)
![]()
- Знайдіть проміжки монотонності функції: (3бали)
![]()
Варіант 2
- Знайдіть похідну функції: (6балів)
а) ![]() г)
г) ![]()
![]() д)
д)![]()
![]() = (9х + 10)82 е)
= (9х + 10)82 е)![]()
- Знайдіть екстремуми функції: (3бали)
![]()
- Знайдіть проміжки монотонності функції: (3бали)
![]()
Варіант 3
- Знайдіть похідну функції: (6балів)
а) ![]() г)
г) ![]()
![]() д)
д)![]()
![]() = (4х
= (4х ![]() 9)72 е)
9)72 е)![]()
- Знайдіть екстремуми функції: (3бали)
![]()
- Знайдіть проміжки монотонності функції: (3бали)
![]()
Варіант 4
- Знайдіть похідну функції: (6балів)
а) ![]() г)
г) ![]()
![]() д)
д)![]()
![]() = (3х + 25)45 е)
= (3х + 25)45 е)![]()
- Знайдіть екстремуми функції: (3бали)
![]()
- Знайдіть проміжки монотонності функції: (3бали)
![]()
Контрольна робота №6
«Інтеграл та його застосування»
Варіант 1
- Обчисліть невизначений інтеграл: (4бали)
![]()
- Обчисліть визначений інтеграл: (3бали)

3. Знайдіть загальний вигляд первісних для функцій: (3бали)
a) f(x) = 2х5 ![]() 3x + 5х 2
3x + 5х 2 ![]()
![]() +
+ ![]()
б) f(x)= 5cos х![]() 3sin x +
3sin x + ![]()
![]()
![]()
4. Розв'яжіть диференціальне рівняння: (2бали)
у'=2х + 6 ![]() cos х +12х5+ еx
cos х +12х5+ еx
Варіант 2
- Обчисліть невизначений інтеграл: (4бали)
![]()
- Обчисліть визначений інтеграл: (3бали)

3. Знайдіть загальний вигляд первісних для функцій: (3бали)
a) f(x) = 10x +2х3 ![]() 3х 4
3х 4 ![]()
![]() +
+ ![]()
б) f(x)=cos х ![]() 9sin x +
9sin x + ![]()
![]()
![]()
4. Розв'яжіть диференціальне рівняння: (2бали)
у'=3х2 + 4 ![]() sin х +21х6+
sin х +21х6+ ![]()
Варіант 3
- Обчисліть невизначений інтеграл: (4бали)
![]()
- Обчисліть визначений інтеграл: (3бали)
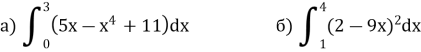
3. Знайдіть загальний вигляд первісних для функцій: (3бали)
a) f(x) = 8х5 ![]() 11x + 5х 4
11x + 5х 4 ![]()
![]() +
+ ![]()
б) f(x)= 10cos х![]() sin x +
sin x + ![]()
![]()
![]()
4. Розв'яжіть диференціальне рівняння: (2бали)
у'=5х + 6 ![]() cos х +3х8+ еx
cos х +3х8+ еx
Варіант 4
- Обчисліть невизначений інтеграл: (4бали)
![]()
- Обчисліть визначений інтеграл: (3бали)

3. Знайдіть загальний вигляд первісних для функцій: (3бали)
a) f(x) = 8x +9х3 ![]() 3х5
3х5 ![]()
![]() +
+ ![]()
б) f(x)=6cos х ![]() 2sin x +
2sin x + ![]()
![]()
![]()
4. Розв'яжіть диференціальне рівняння: (2бали)
у'=8х2 + 6х ![]() sin х +11х6+
sin х +11х6+ ![]()
Контрольна робота №7
«Систематизація та узагальнення фактів і методів планіметрії»
Варіант 1
- Діагоналі ромба дорівнюють 8 см і 6 см. Знайдіть периметр ромба. (2бали)
2. Сторона квадрата рівна 7 см. Визначте довжину діагоналі. (2бали)
3. Більша діагональ і більша основа прямокутної трапеції дорівнюють відповідно 8 см і 6 см. Знайдіть довжину меншої бічної сторони трапеції. (2бали)
4. Знайдіть основу трапеції, якщо її інша основа і середня лінія відповідно дорівнюють: 9 см і 5 см. (3бали)
5. Сторони трикутника дорівнюють 12 см, 16 см і 20 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника. (3бали)
Варіант 2
- Діагоналі ромба дорівнюють 12 см і 16 см. Знайдіть периметр ромба. (2бали)
2. Сторона квадрата рівна 9 см. Визначте довжину діагоналі. (2бали)
3. Більша діагональ і більша основа прямокутної трапеції дорівнюють відповідно 6 см і 4 см. Знайдіть довжину меншої бічної сторони трапеції. (2бали)
4. Знайдіть основу трапеції, якщо її інша основа і середня лінія відповідно дорівнюють: 3 см. і 7 см. (3бали)
5. Сторони трикутника дорівнюють 10 см, 14 см і 18 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника. (3бали)
Варіант 3
- Діагоналі ромба дорівнюють 4 см і 3 см. Знайдіть периметр ромба. (2бали)
- Сторона квадрата рівна 12 см. Визначте довжину діагоналі. (2бали)
3. Більша діагональ і більша основа прямокутної трапеції дорівнюють відповідно 10 см і 8 см. Знайдіть довжину меншої бічної сторони трапеції. (2бали)
4. Знайдіть середню лінію трапеції, якщо її основи дорівнюють: 7 см і 9см. (3бали)
5. Сторони трикутника дорівнюють 14 см, 18 см і 22 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника. (3бали)
Варіант 4
- Діагоналі ромба дорівнюють 10 см і 8 см. Знайдіть периметр ромба. (2бали)
- Сторона квадрата рівна 14 см. Визначте довжину діагоналі. (2бали)
3. Більша діагональ і більша основа прямокутної трапеції дорівнюють відповідно 12 см і 10 см. Знайдіть довжину меншої бічної сторони трапеції. (2бали)
4. Знайдіть середню лінію трапеції, якщо її основи дорівнюють: 2см і 14см. (3бали)
5. Сторони трикутника дорівнюють 8 см, 12 см і 16 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника. (3бали)
Контрольна робота №8
«Вектори і координати»
Варіант 1
-
Знайдіть координати вектора
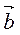 =
= 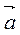 – 2
– 2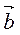 , якщо
, якщо 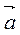 (1; 1),
(1; 1), 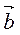 (3; 1). (3бали)
(3; 1). (3бали)
2. Дано три вершини паралелограма ABCD: A(-2; 1), В(-1; 1), С(1; 1). Знайдіть координати вершини D. (3бали)
3. Дано вектори ![]() (4; 2) і
(4; 2) і ![]() (x; -4). При якому значенні х ці вектори колінеарні? (3бали)
(x; -4). При якому значенні х ці вектори колінеарні? (3бали)
4. Трикутник ABC задано координатами його вершин: А(-1; 1), В(0; 2), С(1; 1). Знайдіть зовнішній кут при вершині А. (3бали)
Варіант 2
-
Знайдіть координати вектора
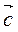 = 2
= 2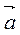 –
– 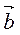 , якщо
, якщо 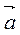 (1; 1),
(1; 1), 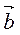 (3; 1). (3бали)
(3; 1). (3бали)
2. Дано три вершини паралелограма ABCD: A(1; -3), В(2; -1), D(3; -3). Знайдіть координати вершини С. (3бали)
3. Дано вектори ![]() (4; 2) і
(4; 2) і ![]() (x; -4). При якому значенні х ці вектори перпендикулярні? (3бали)
(x; -4). При якому значенні х ці вектори перпендикулярні? (3бали)
4. Трикутник ABC задано координатами його вершин: А(3; 5), В(4; 6), С(5; 5). Знайдіть зовнішній кут при вершині А. (3бали)
Варіант 3
-
Знайдіть координати вектора
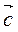 =
= 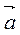 – 3
– 3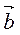 , якщо
, якщо 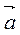 (-1; 2),
(-1; 2), 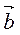 (1; -2). (3бали)
(1; -2). (3бали)
2. Дано три вершини паралелограма ABCD: A(-4; 1), В(-1; 3), D(-2; 1). Знайдіть координати вершини С. (3бали)
3. Дано вектори ![]() (2; 5) і
(2; 5) і ![]() (-6; у). При якому значенні у ці вектори перпендикулярні? (3бали)
(-6; у). При якому значенні у ці вектори перпендикулярні? (3бали)
4. Трикутник ABC задано координатами його вершин: А(1; 3), В(2; 4), С(3; 3). Знайдіть зовнішній кут при вершині А. (3бали)
Варіант 4
-
Знайдіть координати вектора
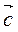 = 3
= 3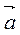 –
– 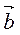 , якщо
, якщо 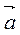 (-1; 2),
(-1; 2), 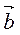 (1; -2). (3бали)
(1; -2). (3бали)
2. Дано три вершини паралелограма ABCD: В(1; 3), С(-1;4), D(-2;2). Знайдіть координати вершини А. (3бали)
-
Дано вектори
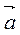 (2; 5) і
(2; 5) і 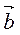 (-6; у). При якому значенні у ці вектори колінеарні? (3бали)
(-6; у). При якому значенні у ці вектори колінеарні? (3бали)
- Трикутник ABC задано координатами його вершин: А(0; 2), В(1; 3), С(2; 2). Знайдіть зовнішній кут при вершині А. (3бали)
Контрольна робота №9
«Паралельність прямих і площин у просторі»
Варіант 1
-
Дано дві паралельні площини
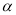 і
і 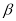 . Точки А і В належать площині
. Точки А і В належать площині 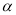 , а точки C і D – площині
, а точки C і D – площині 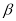 . Відрізки AD і BC перетинаються в точці S. Знайдіть довжину відрізка CD, якщо АВ = 12 см, BS = 4 см, CS = 1 см.
. Відрізки AD і BC перетинаються в точці S. Знайдіть довжину відрізка CD, якщо АВ = 12 см, BS = 4 см, CS = 1 см.
(3бали)
-
Зобразіть куб
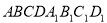 . Позначте точку М – середину ребра DD1. Побудуйте переріз куба площиною, яка проходить через точки А, В1 і М. Знайдіть периметр побудованого перерізу, якщо ребро куба дорівнює 2 см.
. Позначте точку М – середину ребра DD1. Побудуйте переріз куба площиною, яка проходить через точки А, В1 і М. Знайдіть периметр побудованого перерізу, якщо ребро куба дорівнює 2 см.
(3бали)
- Доведіть, що всі точки квадрата лежать в одній площині.
(3бали)
- Скільки площин можна провести через точки А, В, С, якщо АВ = 10 см, ВС = 6 см, АС = 8 см ? (3бали)
Варіант 2
-
Дано дві паралельні площини
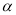 і
і 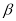 . Точки А і В належать площині
. Точки А і В належать площині 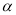 , а точки C і D – площині
, а точки C і D – площині 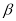 . Відрізки AD і BC перетинаються в точці S. Знайдіть довжину відрізка АВ, якщо CD = 3 см, BS = 4 см, CS = 1 см.
. Відрізки AD і BC перетинаються в точці S. Знайдіть довжину відрізка АВ, якщо CD = 3 см, BS = 4 см, CS = 1 см.
(3бали)
-
Зобразіть куб
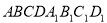 . Позначте точку К – середину ребра DD1. Побудуйте переріз куба площиною, яка проходить через точки С, А1 і К. Знайдіть периметр побудованого перерізу, якщо ребро куба дорівнює 2 см.
. Позначте точку К – середину ребра DD1. Побудуйте переріз куба площиною, яка проходить через точки С, А1 і К. Знайдіть периметр побудованого перерізу, якщо ребро куба дорівнює 2 см.
(3бали)
- Доведіть, що всі точки трикутника лежать в одній площині.
(3бали)
- Скільки площин можна провести через точки А, В, С, якщо АВ = 10 см, ВС = 6 см, АС = 4 см ? (3бали)
Варіант 3
- Дано дві паралельні площини α і β. Промінь SC перетинає площину α в точці А, а площину β – в точці С; промінь SD перетинає площину α в точці В, а площину β – в точціD; SA = 14 см, SC = 42 см, CD = 18 см. Знайти довжину відрізка АВ. (3 бали)
2. Зобразіть куб ![]() . Нехай діагональ грані куба дорівнює 4 см. Побудуйте переріз куба, який проходить через середини ребер AB, ВС i ВВ1 та знайдіть його периметр.
. Нехай діагональ грані куба дорівнює 4 см. Побудуйте переріз куба, який проходить через середини ребер AB, ВС i ВВ1 та знайдіть його периметр.
3.Основа AD трапеції ABCD лежить у площині α, а точки В і С не належать цій площині. Доведіть, що пряма ВС паралельна площині α.
4. Скільки площин можна провести через точки А, В, С? Відповідь обґрунтуйте.
Варіант 4
- Дано паралельні площини α і β. Через точку S, яка не належить жодній із них, проведено прямі а і b, які перетинають площину α в точках A1 і B1, а площину β — в точках А2 і B2, причому SA1 = 8 cm, А1А2 = 12 cm, A2B2 = 25 cм. Знайдіть А1 B1.
(3бали)
-
Зобразіть куб
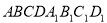 . Нехай діагональ грані куба дорівнює 4 см. Побудуйте переріз куба, який проходить через середини ребер AB, AD i AA1 та знайдіть його периметр.
. Нехай діагональ грані куба дорівнює 4 см. Побудуйте переріз куба, який проходить через середини ребер AB, AD i AA1 та знайдіть його периметр.
(3бали)
-
Доведіть, що всі сторони чотирикутника
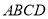 лежать в одній площині, якщо діагоналі цього чотирикутника перетинаються.
лежать в одній площині, якщо діагоналі цього чотирикутника перетинаються.
(3бали)
- Скільки площин можна провести через точку В і пряму α ? Відповідь обґрунтуйте. (3бали)
Контрольна робота №10
«Перпендикулярність прямих і площин у просторі»
Варіант 1
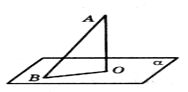
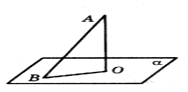
-
Із точки А до площини
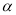 проведено
проведено
похилу АВ і перпендикуляр АО.
Знайдіть ОВ, якщо АВ = ![]() см, АО =
см, АО = ![]() см.
см.
 (3бали)
(3бали)
- В точку О перетину діагоналей прямокутника
ABCD проведено перпендикуляр SO до площини
ABC. Знайдіть SA, якщо SO = 6 см, BD = 16 см.
(3бали)
- Площини квадратів ABCD і ABC1D1 перпендикулярні, АВ=6см. Знайти відстань C1D.
(3бали)
-
З точки М до площини проведено перпендикуляр МО і похилі МА та МВ.
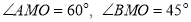 . Знайдіть довжини похилих, якщо проекція меншої похилої дорівнює 8 см. (3бали)
. Знайдіть довжини похилих, якщо проекція меншої похилої дорівнює 8 см. (3бали)
 Варіант 2
Варіант 2
-
Із точки А до площини
 проведено
проведено
похилу АВ і перпендикуляр АО.
Знайдіть АВ, якщо ВО = ![]() см, АО = 1 см.
см, АО = 1 см.
 (3бали)
(3бали)
- В точку О перетину діагоналей прямокутника
ABCD проведено перпендикуляр SO до площини
ABC. Знайдіть SО, якщо SА = 13 см, BD = 10 см.
(3бали)
- Площини квадратів ABCD і ABC1D1 перпендикулярні, АB=8см. Знайти відстань CD1.
(3бали)
-
З точки М до площини проведено перпендикуляр МО і похилі МА та МВ.
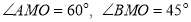 . Знайдіть довжини похилих, якщо проекція меншої похилої дорівнює 6 см. (3бали)
. Знайдіть довжини похилих, якщо проекція меншої похилої дорівнює 6 см. (3бали)
Варіант 3
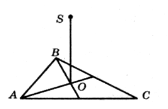
- Із точки О правильного трикутника АВС проведено
перпендикуляр SO до площини трикутника.
Знайдіть ![]() , якщо АО = 10 см, SO = 10 см.
, якщо АО = 10 см, SO = 10 см.
а) 00 б) 300 в) 450 г) 600 д) 900
 (3бали)
(3бали)
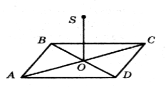
- В точку О перетину діагоналей прямокутника
ABCD проведено перпендикуляр SO до площини
ABC. Знайдіть SA, якщо SO = 8 см, BD = 18 см.
(3бали)
- Відстань від точки S до кожної з вершин квадрата АВСD дорівнює 10 см. Знайдіть відстань від точки S до площини квадрата АВСD, якщо його діагональ дорівнює 12 см.
(3бали)
- Точка S розташована на відстані 6 см від кожної з вершин прямокутника АВСD і віддалена від його площини на 4 см. Знайдіть сторони прямокутника, якщо одна з них удвічі більша за другу.
(3бали)
 Варіант 4
Варіант 4
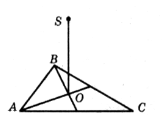
- Із точки О правильного трикутника АВС проведено
перпендикуляр SO до площини трикутника.
Знайдіть ![]() , якщо SC = 10 см, SO = 5 см.
, якщо SC = 10 см, SO = 5 см.
а) 00 б) 300 в) 450 г) 600 д) 900
 (3бали)
(3бали)
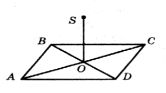
- В точку О перетину діагоналей прямокутника
ABCD проведено перпендикуляр SO до площини
ABC. Знайдіть SО, якщо SА = 15 см, BD = 12 см.
(3бали)
- Відстань від точки S до кожної з вершин квадрата АВСD дорівнює 10 см. Знайдіть діагональ квадрата АВСD, якщо відстань від точки S до його площини дорівнює 6 см.
(3бали)
- Точка S розташована на відстані 6 см від кожної з вершин прямокутника АВСD і віддалена від його площини на 4 см. Знайдіть сторони прямокутника, якщо одна з них на 4 см більша за другу.
(3бали)
Контрольна робота №11
«Многогранники. Об’єми та площі поверхонь многогранників»
Варіант 1
- Знайдіть площу бічної поверхні правильної трикутної призми, сторона основи якої дорівнює 3 см, а бічне ребро – 5 см. (2бали)
2. Знайдіть об'єм правильної чотирикутної піраміди, сторона основи якої дорівнює 2 см, а висота піраміди – 6 см. (2бали)
3. У правильній трикутній піраміді сторона основи дорівнює 8 см, а апофема – 3 см. Знайдіть бічне ребро піраміди. (4бали)
4. Бічні ребра трикутної піраміди попарно перпендикулярні й мають довжини 3 см, 4 см і 5 см. Знайдіть її об'єм. (4бали)
Варіант 2
- Знайдіть площу бічної поверхні правильної трикутної піраміди, якщо сторона основи дорівнює 12 см, а апофема 10 см. (2бали)
2.Знайдіть об'єм правильної чотирикутної призми, сторона основи якої дорівнює 3 см, а бічне ребро – 5 см. (2бали)
3.У правильній чотирикутній піраміді висота дорівнює 6 см, а діагональ основи – 16 см. Знайдіть бічне ребро піраміди. (4бали)
4.В основі піраміди лежить квадрат зі стороною 5 см. Обчисліть об'єм піраміди, якщо її висота дорівнює 6 см. (4бали)
Варіант 3
- Знайдіть площу бічної поверхні правильної чотирикутної піраміди, якщо сторона основи дорівнює 16 см, а бічне ребро – 10 см. (2бали)
- Знайдіть об'єм прямої чотирикутної призми, в основі якої лежить ромб з діагоналями 12 см і 16 см, а бічне ребро – 10 см. (2бали)
3. В основі правильної призми лежить трикутник із стороною 4 см, а її бічне ребро дорівнює 10 см. Знайдіть площу бічної поверхні цієї призми. (4бали)
4. В основі правильної піраміди лежить квадрат зі стороною 10 см. Висота піраміди дорівнює 12 см. Знайдіть площу поверхні та об'єм піраміди. (4бали)
Варіант 4
- Знайдіть площу бічної поверхні правильної трикутної піраміди, кожне ребро якої дорівнює 2 см. (2бали)
2. Знайдіть об'єм правильної чотирикутної піраміди, сторона основи якої дорівнює 6 см, а висота – 10 см. (2бали)
- В основі прямої призми лежить прямокутний трикутник з катетами 6 см і 8 см. Бічне ребро дорівнює найбільшому ребру основи. Знайдіть площу поверхні та об'єм призми. (4бали)
4. В основі піраміди лежить ромб з діагоналями 6 см і 8 см. Висота піраміди дорівнює 10 см. Знайдіть об'єм піраміди. (4бали)
Контрольна робота №12
«Тіла обертання. Об’єми та площі тіл обертання»
Варіант 1
1. Осьовий переріз циліндра – квадрат, площа його дорівнює 100 см2. Знайти площу основи циліндра. (2бали)
2. Якщо радіус кулі дорівнює 15 см, а точка А знаходиться від центра кулі на відстані 20 см, то точка А лежить: (1бал)
а) всередині кулі б) на поверхні кулі в) поза кулею
3. Якщо висота конуса дорівнює 3 см, а діаметр основи – 8 см, то площа бічної поверхні конуса дорівнює: (2бали)
а) 24π см2 б) 20π см2 в) 15π см2 г) 12π см2
4. Висота циліндра АВ=6см, радіус основи СВ=8см. Знайдіть довжину відрізка АС. (3бали)
5. Якщо кулю радіуса 5 см перетнути площиною, яка знаходиться на відстані 3 см від центра кулі, то площа круга перерізу дорівнюватиме: (4бали)
а) 25π см2 б) 9π см2 в) 16 см2 г) 16π см2
Варіант 2
1. Осьовий переріз циліндра – квадрат, периметр його дорівнює 16см. Знайти площу основи циліндра. (2бали)
2. Якщо радіус кулі дорівнює 15 см, а точка А знаходиться від центра кулі на відстані 10 см, то точка А лежить: (1бал)
а) поза кулею б) на поверхні кулі в) всередині кулі
3. Якщо висота осьового перерізу циліндра дорівнює 10 см, а діаметр основи дорівнює 8 см, то площа бічної поверхні циліндра дорівнює: (2бали)
а) 24π см2 б) 48π см2 в) 60π см2 г) 80π см2
4. Радіус основи конуса 3м, висота 4м. Знайдіть твірну. (3бали)
5. Якщо кулю радіуса 5 см перетнути площиною, яка знаходиться на відстані 4 см від центра кулі, то площа круга перерізу дорівнюватиме: (4бали) а)25π см2 б) 9π см2 в) 16 см2 г) 16π см2
Варіант 3
1. Осьовий переріз циліндра – квадрат, площа його дорівнює 1000 см2. Знайти площу основи циліндра. (2бали)
2. Якщо радіус кулі дорівнює 12 см, а точка А знаходиться від центра кулі на відстані 18 см, то точка А лежить: (1бал)
а) всередині кулі б) на поверхні кулі в) поза кулею
3. Обчисліть площу бічної поверхні конуса, в якому твірна дорівнює 13 см, а висота становить 12 см. (2бали)
а) ![]() см2 б)
см2 б) ![]() см2 в)
см2 в) ![]() см2 г)
см2 г) ![]() см2 д)
см2 д) ![]() см2
см2
4. Висота циліндра АВ=8см, радіус основи СВ=10см. Знайдіть довжину відрізка АС. (3бали)
5. В кулі проведено січну площину на відстані 1 см від її центра. Знайдіть радіус перерізу, якщо радіус кулі дорівнює ![]() см. (4бали)
см. (4бали)
а) 1 см б) ![]() см в)
см в) ![]() см г) 2 см д)
см г) 2 см д) ![]() см
см
Варіант 4
1. Осьовий переріз циліндра – квадрат, периметр його дорівнює 32см. Знайти площу основи циліндра. (2бали)
2. Якщо радіус кулі дорівнює 8 см, а точка А знаходиться від центра кулі на відстані 10 см, то точка А лежить: (1бал)
а) поза кулею б) на поверхні кулі в) всередині кулі
3. Знайдіть об'єм конуса, осьовим перерізом якого є рівносторонній трикутник зі стороною 12 см. (2бали)
а) ![]() см3 б)
см3 б) ![]() см3 в)
см3 в) ![]() см3 г)
см3 г) ![]() см3 д)
см3 д) ![]() см3
см3
4. Радіус основи конуса 5м, висота 6м. Знайдіть твірну. (3бали)
5. В кулі проведено січну площину на відстані 1 см від її центра. Знайдіть радіус кулі, якщо радіус перерізу дорівнює ![]() см. (4бали) а) 1 см б)
см. (4бали) а) 1 см б) ![]() см в)
см в) ![]() см г) 2 см д)
см г) 2 см д) ![]() см
см
Контрольна робота №13
«Елементи теорії ймовірностей та математичної статистики»
Варіант 1
- Дано: А = {1,3,5,7}, B = {1,5,7,9}. Знайдіть АВ, АВ. (1бал)
-
В ящику 50 куль: 36 жовтих і 14 синіх. З ящика навмання виймають одну кулю. Визначити ймовірність того, що ця куля: (3бали)
а) жовта б) синя. - Скількома способами можна вишикувати на фізичному вихованні 13 студентів? (2бали)
- До складу профкому обрано 12 осіб. Серед них потрібно вибрати голову, його заступника і секретаря. Скількома способами можна це зробити? (3бали)
-
Знайти моду і середнє значення вибірки:
6; 9; 8; 7; 5; 4; 4; 32; 9; 8; 4; 1 (1бал) - У нас є 9 різних книг із серії «Цікава математика». Скількома способами можна розставити їх на полиці? (2бали)
Варіант 2
- Дано: А = {1,4,6,8}, B = {1,6,8,9}. Знайдіть АВ, АВ. (1бал)
- У ящику лежать 6 червоних, 4 синіх, 18 зелених олівців. Ви навмання виймаєте олівець. Яка ймовірність того, що це червоний олівець? жовтий олівець? синій олівець? (3бали)
- Скількома способами можна розмістити 17 автомобілів різного кольору в один ряд? (2бали)
- Скількома способами можна вибрати 3 різні фарби із 15 різних фарб? (3бали)
-
Знайти моду і середнє значення вибірки: (1бал)
13; 12; 12; 13; 17; 15; 18; 18; 11; 18 - Скількома способами 5 людей можуть стати в чергу до квиткової каси? (2бали)
Варіант 3
- Дано: А = {2,3,11 ,4}, B = {2,11,4,9}. Знайдіть АВ, АВ. (1бал)
-
В ящику 60 куль: 46 жовтих і 14 синіх. З ящика навмання виймають одну кулю. Визначити ймовірність того, що ця куля: (3бали)
а) жовта б) синя. - Скількома способами можна розташувати 8 гостей за круглим столом? (2бали)
- До складу профкому обрано 17 осіб. Серед них потрібно вибрати голову, його заступника і секретаря. Скількома способами можна це зробити? (3бали)
-
Знайти моду і середнє значення вибірки: (1бал)
2; 11; 8; 7; 3; 5; 5; 32; 11; 8; 5; 1 - У нас є 7 різних книг із серії «Цікава математика». Скількома способами можна розставити їх на полиці? (2бали)
Варіант 4
- Дано: А = {10,4,6,8}, B = {10,6,8,9}. Знайдіть АВ, АВ. (1бал)
- У ящику лежать 4 червоних, 6 синіх, 12 зелених олівців. Ви навмання виймаєте олівець. Яка ймовірність того, що це червоний олівець? жовтий олівець? синій олівець? (3бали)
- Скількома способами можна розмістити 15 автомобілів різного кольору в один ряд? (2бали)
- Скількома способами можна вибрати 4 різні чашки із 20 різних чашок? (3бали)
-
Знайти моду і середнє значення вибірки: (1бал)
3; 8; 8; 3; 17; 15; 5; 5; 11; 5 - Скількома способами 6 студентів можуть стати в чергу в столовій? (2бали)
Список використаних джерел
- Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики (навчальний посібник для студентів ВНЗ І-ІІ р.а.) – К.: Вища школа, 2001.
- Афанасьєва О.М. та інші. Дидактичний матеріал з геометрії, 10-11 кл. – Тернопіль: Навчальна книга – Богдан, 2003.
- Бевз Г.П. Алгебра і початки аналізу (підручник для шкіл, ліцеїв, гімназій гуманітарного напряму), 10-11 кл. – К.: ТОВ «Бліц», 2005.
- Бевз Г.П. Алгебра і початки аналізу: Підручник для 10-11 класу загальноосвітніх навчальних закладів – К.: Освіта, 2005.
- Бевз Г.П. та ін. «Геометрія 10 клас», К. Генеза, 2010.
- Богомолов М.В. «Практичні заняття з математики».
- Бродський Я.С., Павлов О.Л. Математика. Тести для самостійної роботи та контролю знань, 10-11 кл. – Тернопіль: Навчальна книга – Богдан, 2003.
- Бродський Я.С. Тести із стереометрії, 10-11 кл. – Тернопіль: Навчальна книга – Богдан, 2004.
- Бурда М.І., Дубинчук О.С., Мальований Ю.І. Математика (підручник для навчальних закладів освіти гуманітарного профілю), 10-11 кл. – К.: Освіта, 2001.
- Гап’юк Я., Гричишин Я. і ін. «Математика 10» рівень стандарту, Тернопіль. 2010 .
- Збірник завдань для державної підсумкової атестації з математики. Алгебра та початки аналізу. За ред. Слєпкань З.І. 11 кл. – Х.: Гімназія, 2005.
- Збірник завдань для державної підсумкової атестації з математики. Геометрія. За ред. Слєпкань З.І. 11 кл. – Х.: Гімназія, 2005.
- Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 10-11 кл. загальноосвітніх навчальних закладів – К.: Школяр, 2004, Освіта, 2001.
- Прокопенко Н.С., Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика. Збірник завдань для тематичного оцінювання знань, 10, 11 кл. – К.: КІМО, 2001.
- Роєва Т.Г. Завдання для поточного оцінювання. Алгебра. Книга для вчителя. 11 кл. – К.: Країна мрій, 2005.
- Роєва Т.Г. Завдання для поточного оцінювання. Геометрія. Книга для вчителя. 11 кл. – К.: Країна мрій, 2005.
- Роєва Т.Г., Адруг Л.М. Алгебра і початки аналізу. Завдання для тематичного оцінювання. 10, 11 кл. – К.: Країна мрій, 2007.
- Роєва Т.Г., Адруг Л.М. Геометрія Завдання для тематичного оцінювання. 10, 11 кл. – К.: Країна мрій, 2007.
- Роєва Т.Г., Адруг Л.М. Математика. Інтегровний курс. Тематичне оцінювання. 10, 11 кл. – К.: Країна мрій, 2007.
- Слєпкань З.І., Грохольська А.В. Збірник задач з алгебри і початків аналізу, 10-11 кл. – К.: Підручники і посібники, 2003.
- Стадник Л.Г., Гальперина А.Р. Варіанти завдань для тематичного оцінювання навчальних досягнень учнів. Алгебра. Геометрія. 10 кл. – Х.: Ранок, 2003.
- Стадник Л.Г., Маркова І.С. Варіанти завдань для тематичного оцінювання навчальних досягнень учнів. Алгебра. Геометрія. 11 кл. – Х.: Ранок, 2003.
- Хроленко Н.Ф., Леонова С.Ю. Завдання для поточного оцінювання. Алгебра. Книга для вчителя. 10 кл. – К.: Країна мрій, 2003.
- Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник) , 10-11 кл. – К.: Зодіак – ЕКО, 2002.
1


про публікацію авторської розробки
Додати розробку
