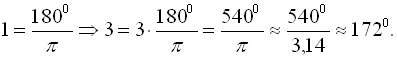Навчальний посібник з математики "Тригонометрія"
1.ТРИГОНОМЕТРИЧНІ ПЕРЕТВОРЕННЯ
1.1. Радіанна система вимірювання кутів і дуг
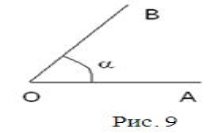
Кут – це геометрична фігура, утворена двома променями, які виходять з однієї точки, названої вершиною кута (рис. 9). Слово “кут” заміняють символом ∠: ∠АОВ=∠ВОА=∠α.
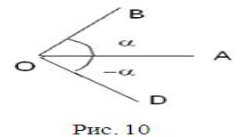
Кут можна розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки О. Промінь можна обертати навколо своєї початкової точки у двох напрямках: за годинниковою стрілкою і проти годинникової стрілки. Напрям обертання проти годинникової стрілки умовно називають додатним, а за годинниковою стрілкою – від’ємним.
Відповідно до цього кути і дуги, отримані обертанням променя проти годинникової стрілки, вважаються додатними, а кути і дуги, отримані обертанням променя за годинниковою стрілкою, вважаються від’ємними (рис. 10).
Якщо сторони кута утворюють пряму, то такий кут називається розгорнутим.
Якщо промінь робить повний оберт навколо своєї початкової точки, то отриманий кут називається повним.
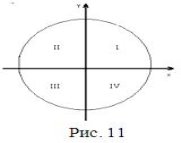
Осі абсцис (Ох) і ординат (Оу) ділять повний кут (коло) на чотири чверті (I - IV), або чотири квадранта (рис. 11).
Кути вимірюються в градусах і радіанах. Кут в 1 градус – це кут, що його опише промінь, зробивши 1/360 частину повного оберту навколо своєї початкової точки проти годинникової стрілки.
1/60 частина градуса називається хвилиною (позначка ![]() ).
).
1/60 частина хвилини називається секундою (позначка ![]() ).
).
Центральним кутом у колі називається кут, вершина якого знаходиться в його центрі.
Кут в 1 радіан – це центральний кут, який спирається на таку дугу кола, довжина якої дорівнює радіусу цього кола. Слово “радіан” звичайно не пишуть. Таким чином, якщо |АВ|=R, |OA|=|OB|=R, то ∠АОВ=∠α=1, тобто кут α дорівнює одному радіану (рис. 12).
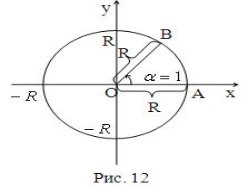
Оскільки довжина всього кола дорівнює 2πR, то повний кут складає ![]() радіан, тому що
радіан, тому що 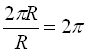 . Оскільки повний кут дорівнює 360˚, то
. Оскільки повний кут дорівнює 360˚, то ![]() 360˚. Звідси 1 радіан =
360˚. Звідси 1 радіан = 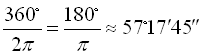 (57 градусів, 17 хвилин, 45 секунд).
(57 градусів, 17 хвилин, 45 секунд).
Таким чином, користуючись співвідношеннями ![]() ,
,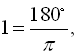
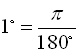 , можна переходити від градусів до радіанів і навпаки.
, можна переходити від градусів до радіанів і навпаки.
Приклад 1
а) Виразити в радіанах кут у 45°;
б) Виразити в градусах кут у 3 радіана.
Розв’язання:
а) 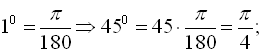
1.2. Визначення тригонометричних функцій
Розглянемо спочатку тригонометричні функції гострого кута, які можна ввести за допомогою прямокутного трикутника (рис. 13).
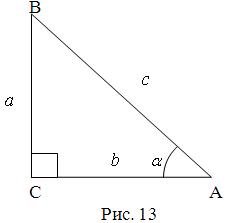
Нехай у прямокутному трикутнику ∠ACB = 90˚ , |BC|=a, |AC|=b, |AB|=c.
Синусом кута називається відношення протилежного катета до гіпотенузи:
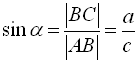
Косинусом кута називається відношення прилеглого катета до гіпотенузи:
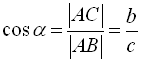
Тангенсом кута називається відношення протилежного катета до прилеглого:
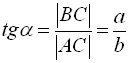
Котангенсом кута називається відношення прилеглого катета до протилежного:
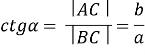
Розглянемо тригонометричні функції довільних значень аргументу.
Маємо прямокутну систему координат x0y на площині і коло одиничного радіуса, що має центр у початку координат (рис. 14).
Таке коло називається одиничним колом чи тригонометричним колом.
Синусом кута називається відношення ординати точки ![]() до радіуса.
до радіуса.
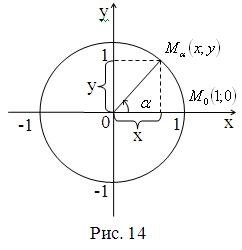
Косинусом кута називається відношення абсциси точки ![]() до радіуса.
до радіуса.
Таким чином, ![]() ,
, 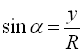 . Оскільки
. Оскільки 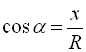 , то
, то ![]() ,
, ![]() .
.![]() і
і ![]() можна розглядати як проекції на осі координат одиничного вектора
можна розглядати як проекції на осі координат одиничного вектора ![]() . Таким чином, можна стверджувати, що синус кута
. Таким чином, можна стверджувати, що синус кута ![]() дорівнює ординаті, а косинус – абсцисі вектора одиничної довжини, що виходить з початку координат і утворює з додатним напрямом осі
дорівнює ординаті, а косинус – абсцисі вектора одиничної довжини, що виходить з початку координат і утворює з додатним напрямом осі ![]() кут
кут ![]() . Оскільки
. Оскільки ![]() , то
, то
співвідношення ![]() (1) називається основною тригонометричною тотожністю.
(1) називається основною тригонометричною тотожністю.
Тангенсом кута ![]() називається відношення ординати точки
називається відношення ординати точки ![]() до її абсциси:
до її абсциси: ![]() .
. 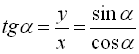 (2)
(2)
Котангенсом кута називається відношення абсциси точки ![]() до її ординати:
до її ординати: ![]() .
. 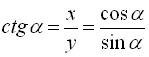 (3)
(3)
Обернені тригонометричні функції відповідно позначаються:
arcsin, arccos, arctg, arcctg.
Знаки тригонометричних функцій наведені на рис. 15.
![]()
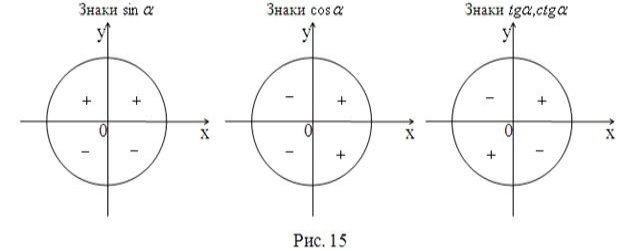
Зобразимо таблицю значень тригонометричних функцій деяких кутів, які найбільш часто використовуються на практиці (табл. 1).
Таблиця 1
Значення тригонометричних функцій для деяких значень аргументу
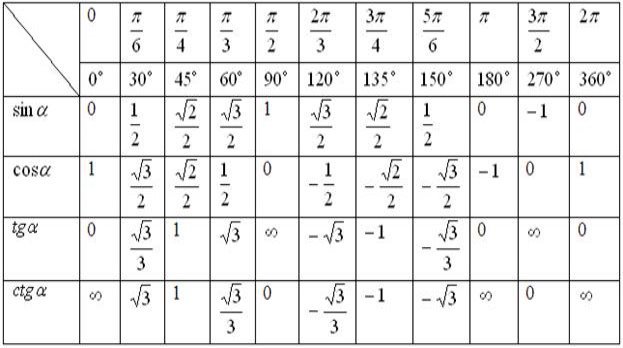
Символ (нескінченність) означає, що ![]() або
або ![]() при відповідних значеннях аргументу не визначені і набувають великих значень за модулем.
при відповідних значеннях аргументу не визначені і набувають великих значень за модулем.
Основні співвідношення між тригонометричними функціями того самого аргументу
З означення тангенса та котангенса кута, ми отримали тригонометричні тотожності 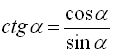 ;
; 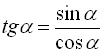 .
.
Перемноживши їх між собою, отримаємо:
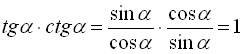 . (6)
. (6)
Розділивши почленно основну тригонометричну тотожність (1) на ![]() , отримаємо:
, отримаємо:
![]()
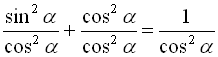
![]() (7)
(7)
Розділимо почленно 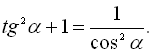 на
на ![]() і отримаємо
і отримаємо ![]() . (8)
. (8)
1.3. Вираження одних тригонометричних функцій через інші
З основної тригонометричної тотожності випливає, що ![]() , тоді
, тоді
![]() , (9)
, (9)
а отже ![]() . (10)
. (10)
У формулах (9) і (10) знаки «+» або «–» вибираються в залежності від того, у якій чверті закінчується кут ![]() . Так, якщо
. Так, якщо ![]() закінчується в І або ІІ чверті, то беремо знак «+», якщо в ІІІ або ІV чверті, то знак «–» у формулі (9). У формулі (10) для кутів, що закінчуються в І або ІV чвертях, потрібно взяти знак «+», а якщо кути закінчуються в ІІ або ІІІ чвертях, то знак «–».
закінчується в І або ІІ чверті, то беремо знак «+», якщо в ІІІ або ІV чверті, то знак «–» у формулі (9). У формулі (10) для кутів, що закінчуються в І або ІV чвертях, потрібно взяти знак «+», а якщо кути закінчуються в ІІ або ІІІ чвертях, то знак «–».
Виразимо ![]() через
через ![]() з формули (8):
з формули (8):
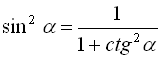
![]()
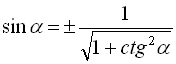 . (11)
. (11)
З формули (6) випливає, що 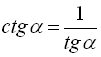 , тоді формулу (11) можна записати через
, тоді формулу (11) можна записати через ![]() :
:
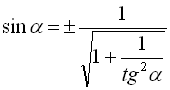
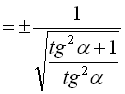
![]()
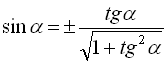 . (12)
. (12)
З формули (7) слідує, що 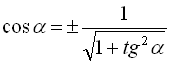 , (13)
, (13)
або ![]() через
через ![]() буде мати вигляд
буде мати вигляд
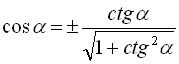 . (14)
. (14)
Приклад 2
Визначити знаки виразів: а) ![]() ; б)
; б) ![]() .
.
Розв’язання:
Зазначимо, що ![]() , але, з іншого боку,
, але, з іншого боку, ![]() радіан. Тому
радіан. Тому 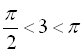 ,
, 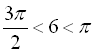 . Звідси кут
. Звідси кут ![]() закінчується в ІІ чверті, а кут
закінчується в ІІ чверті, а кут ![]() закінчується в ІV чверті. Тоді за таблицею знаків тригонометричних функцій,
закінчується в ІV чверті. Тоді за таблицею знаків тригонометричних функцій, ![]() ,
, ![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() .
.
Приклад 3
Обчислити значення усіх тригонометричних функцій кута ![]() , якщо
, якщо 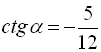 ,.
,.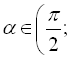
![]()
Розв’язання:
Застосовуючи формули (8), (12), (10), (6), (4), (5), маємо 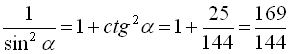 , звідки
, звідки 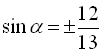 , а оскільки у другій чверті синус додатний, то знаходимо
, а оскільки у другій чверті синус додатний, то знаходимо 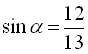 . Далі
. Далі 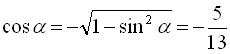 (оскільки косинус від’ємний у другій чверті),
(оскільки косинус від’ємний у другій чверті), 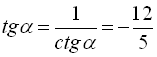 .
.
Відповідь: 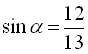 ;
; 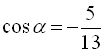 ;
; 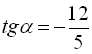 .
.
Приклад 4
Спростити вираз ![]() .
.
Розв’язання:
Розкладемо суму кубів і, застосовуючи формулу (1), дістаємо 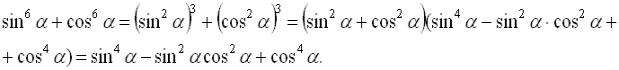
Далі маємо ![]()
![]() .
.
Відповідь: ![]() .
.
Приклад 5
Спростити вираз 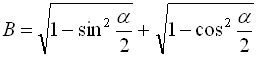 , якщо
, якщо ![]() .
.
Розв’язання:
З основної тригонометричної тотожності випливає, що 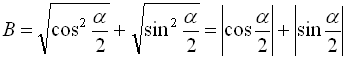 .
.
Оскільки ![]() , то
, то 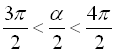 , отже кут
, отже кут ![]() закінчується в ІV чверті, тоді
закінчується в ІV чверті, тоді 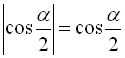 ,
, 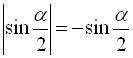 . Звідси
. Звідси 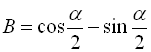 .
.
Відповідь: 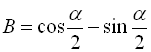 .
.
Приклад 6
Дано: ![]() .
.
Знайти: а) ![]() ; б)
; б) ![]() .
.
Розв’язання:
а) Піднесемо обидві частини початкового виразу до квадрата: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
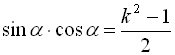 ;
;
б) ![]()
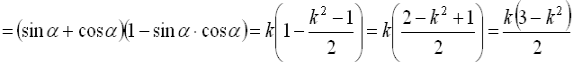 .
.
В даному прикладі ми врахували, що якщо ![]() , то
, то 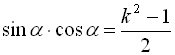 відповідно до висновку пункту а).
відповідно до висновку пункту а).
Відповідь: а) 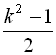 ; б)
; б) 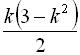 .
.
1.4. Формули додавання і віднімання аргументів
Для будь-яких дійсних чисел ![]() і
і ![]() справедливі формули:
справедливі формули:
![]() ; (15)
; (15)
![]() ; (16)
; (16)
![]() ; (17)
; (17)
![]() ; (18)
; (18)
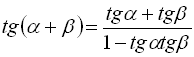 ; (19)
; (19)
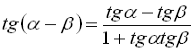 . (20)
. (20)
Формула (19) справедлива при ![]()
![]()
![]() відмінних від
відмінних від 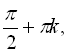
![]() . Формула (20) справедлива при
. Формула (20) справедлива при ![]()
![]()
![]() відмінних від
відмінних від 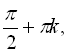
![]() .
.
Приклад 7
Обчислити ![]() .
.
Розв’язання:
Для початку ![]() можна розписати, як
можна розписати, як ![]() .
.
Скориставшись формулою (16), при ![]() ,
, ![]() отримаємо
отримаємо
![]() .
.
Користуючись таблицею значень тригонометричних функцій, маємо
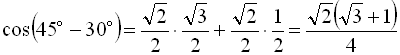 .
.
Отже, ![]()
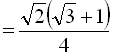 .
.
Відповідь: 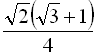 .
.
Приклад 8
Знайти 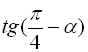 , якщо
, якщо 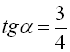 .
.
Розв’язання:
Скористаємося формулою (20) і врахуємо, що 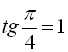 . Маємо
. Маємо 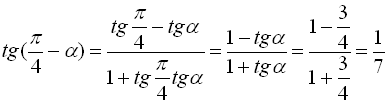 .
.
Відповідь: ![]() .
.
1.5. Основні формули тригонометрії
Крім тригонометричних формул, з якими ми познайомилися раніше, існує ряд формул, що їх відносять до основних формул тригонометрії, а саме:
* Формули подвійного і потрійного аргументів:
![]() ; (21)
; (21)
![]() ; (22)
; (22)
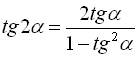
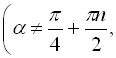
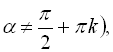
![]()
![]() ; (23)
; (23)
![]() ; (24)
; (24)
![]() ; (25)
; (25)
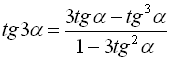 . (26)
. (26)
* Формули пониження степеня:
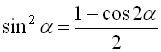 ; (27)
; (27)
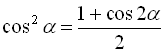 . (28)
. (28)
* Формули перетворення добутку тригонометричних функцій у суму:
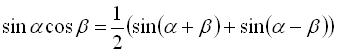 ; (29)
; (29)
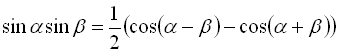 ; (30)
; (30)
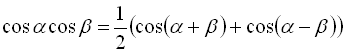 . (31)
. (31)
* Формули перетворення суми і різниці однойменних тригонометричних функцій:
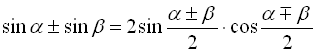 ; (32)
; (32)
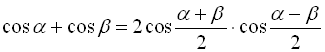 ; (33)
; (33)
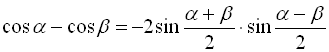 ; (34)
; (34)
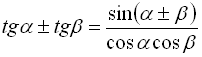
![]()
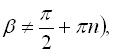
![]() ; (35)
; (35)
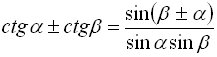
![]()
![]()
![]() . (36)
. (36)
* Формули, які дають раціональний вираз тригонометричних функцій через тангенс половинного аргументу:
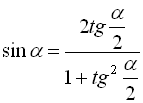 ; (37)
; (37)
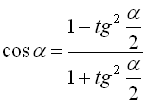
![]()
![]() ; (38)
; (38)
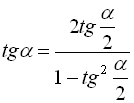
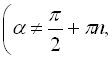
![]()
![]()
![]() . (39)
. (39)
* Формули тригонометричних функцій половинного аргументу:
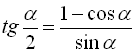
![]()
![]() ; (40)
; (40)
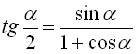
![]()
![]() ; (41)
; (41)
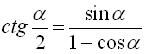
![]()
![]() ; (42)
; (42)
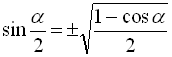 ; (43)
; (43)
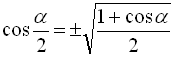 ; (44)
; (44)
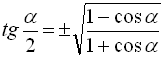 . (45)
. (45)
Знак перед радикалом в останніх трьох формулах залежить від того, в якій координатній чверті знаходиться кут ![]() .
.
1.6. Формули зведення
Формулами зведення називаються співвідношення, за допомогою яких значення тригонометричних функцій аргументів 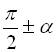 ,
, ![]() ,
,
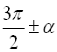 ,
, ![]() виражаються через значення
виражаються через значення ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для полегшення запам’ятовування формул зведення можна користуватися такими правилами:
1) якщо у формулах містяться кути ![]() і
і ![]() , то найменування функції не змінюється; якщо ж у формулах містяться кути
, то найменування функції не змінюється; якщо ж у формулах містяться кути ![]() і
і ![]() , то найменування функції змінюється на подібне (синус – на косинус, тангенс – на котангенс і навпаки);
, то найменування функції змінюється на подібне (синус – на косинус, тангенс – на котангенс і навпаки);
2) щоб визначити знак у правій частині формули («+» або « –»), досить, вважаючи кут ![]() гострим, визначити знак виразу, який стоїть у лівій частині формули; при цьому перед функцією кута
гострим, визначити знак виразу, який стоїть у лівій частині формули; при цьому перед функцією кута ![]() ставлять такий знак, який має зведена функція кутів
ставлять такий знак, який має зведена функція кутів 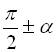 ,
, ![]() ,
, 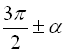 ,
, ![]() .
.
Наприклад, 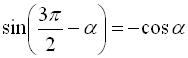 ;
; ![]() .
.
Приклад 9
Звести до тригонометричної функції гострого кута:
а) ![]() ; б)
; б) 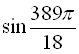 .
.
Розв’язання:
Врахуємо, що період для ![]() і
і ![]() дорівнює
дорівнює ![]() або
або ![]() .
.
а)![]() ;
;
б) 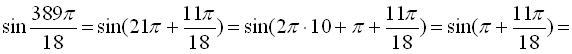
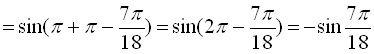 .
.
Відповідь: а) ![]() ; б)
; б) 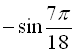 .
.
Приклад 10
Обчислити ![]() .
.
Розв’язання:
Виконаємо перетворення, враховуючи періодичність:
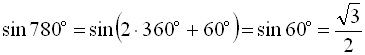 ;
;
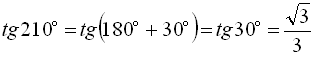 ;
;
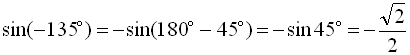 ;
;
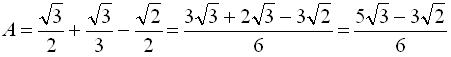 .
.
Відповідь: 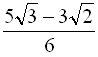 .
.
1.7. Приклади на доведення тригонометричних тотожностей
При доведенні тотожностей звичайно використовують такі способи:
1) Вираз, який стоїть в одній частині тотожності, за допомогою тотожних перетворень приводять до виразу, який стоїть в іншій частині тотожності;
2) вираз, який стоїть у лівій і правій частинах тотожності, приводять до одного і того ж виду;
3) доводять, що різниця між лівою і правою частинами тотожності дорівнює нулю.
Приклад 11
Довести тотожність:
![]() .
.
Розв’язання:
Перетворимо ліву частину даної тотожності:
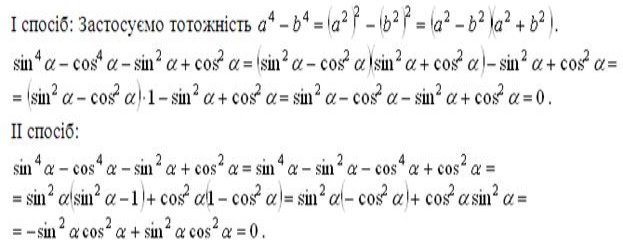
Приклад 12
Довести тотожність:
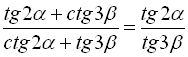 .
.
Розв’язання:
Позначимо ліву частину рівності А, а праву – В:
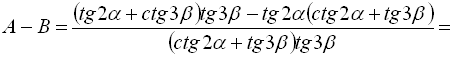
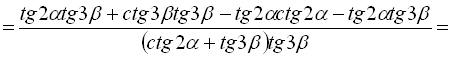
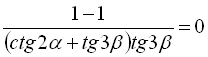 , тобто
, тобто ![]() . Тотожність доведено.
. Тотожність доведено.
Приклад 13
Довести тотожність:
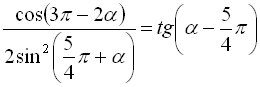 .
.
Розв’язання:
Спростимо ліву частину тотожності, яку потрібно довести:
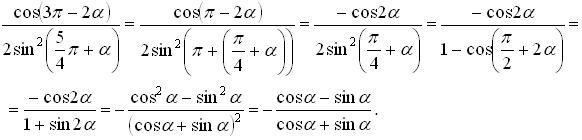 .
.
Тепер спростимо праву частину даної тотожності:
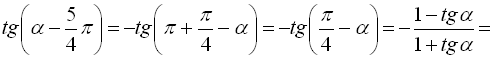
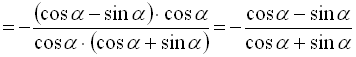 .
.
Як бачимо, ліва і права частини однакові.
Тотожність доведено.
1.8. Розв’язування прикладів на спрощення тригонометричних виразів
Приклад 14
Спростити вираз ![]() .
.
Розв’язання:
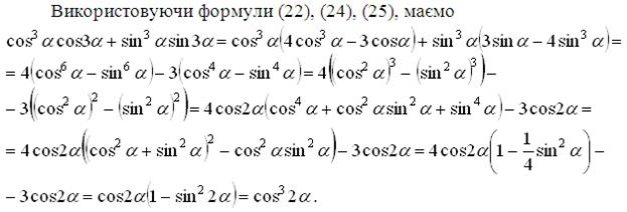 Відповідь:
Відповідь: ![]() .
.
Приклад 15
Спростити та обчислити
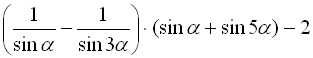 , якщо
, якщо ![]() .
.
Розв’язання:
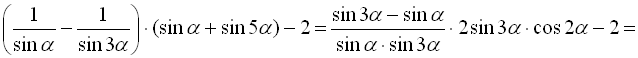
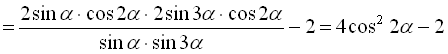 . Якщо
. Якщо ![]() , тоді
, тоді
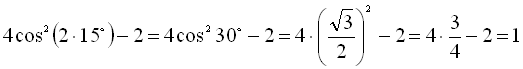 .
.
Відповідь: 1.
Приклад 16
Спростити та обчислити
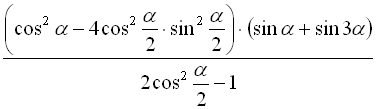 , якщо
, якщо 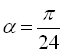 .
.
Розв’язання:
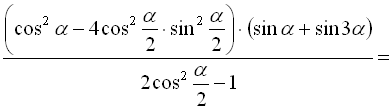
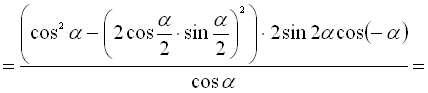
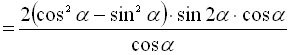
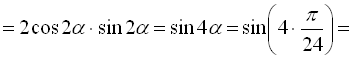
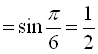 .
.
Відповідь: 0,5.
Приклад 17
Перетворити у добуток вираз 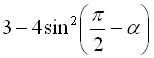 .
.
Розв’язання:
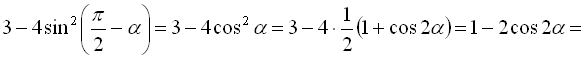
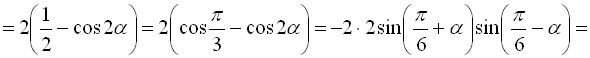
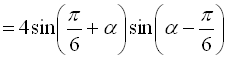 .
.
Відповідь: 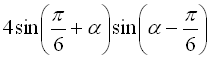 .
.
Приклад 18
Обчислити ![]() .
.
Розв’язання:
За формулами зведення маємо
![]() ;
; ![]() ;
;
![]() ;…;
;…;
![]() .
.
Тоді вираз можна записати в такий спосіб:
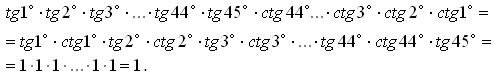
Відповідь: 1.
1.9. Властивості тригонометричних функцій
1.9.1. Парність і непарність тригонометричних функцій
Якщо при повороті навколо точки О на кут![]() початковий радіус ОА переходить у радіус ОВ, то при повороті на кут
початковий радіус ОА переходить у радіус ОВ, то при повороті на кут ![]() початковий радіус ОА перейде у радіус
початковий радіус ОА перейде у радіус ![]() , симетричний ОВ відносно осі абсцис (рис. 16).
, симетричний ОВ відносно осі абсцис (рис. 16).
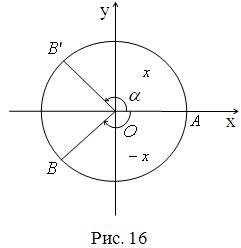
Абсциси точок В і ![]() рівні, а ординати рівні за модулем, але протилежні за знаком. Це означає, що
рівні, а ординати рівні за модулем, але протилежні за знаком. Це означає, що![]() ,
, ![]() ,
,
![]() ,
, ![]() . Таким чином, функції
. Таким чином, функції
![]() ,
, ![]() ,
, ![]() непарні, а функція
непарні, а функція ![]() парна.
парна.
Приклад 19
Дослідити на парність функції: а) ![]() ;
;
б) 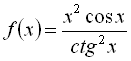 ; в)
; в) ![]() .
.
Розв’язання:
а)![]()
![]()
![]()
![]()
![]() функція
функція ![]() є непарною.
є непарною.
б)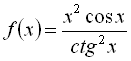
![]()
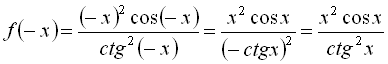
![]()
![]() функція
функція 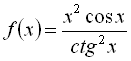 є парною.
є парною.
1.9.2. Періодичність тригонометричних функцій
Для періодичної функції ![]() виконується рівність
виконується рівність ![]() , де Т – відмінне від нуля число, назване періодом функції. Кожна періодична функція має велику кількість періодів, тобто якщо Т – період, то пТ – період, де
, де Т – відмінне від нуля число, назване періодом функції. Кожна періодична функція має велику кількість періодів, тобто якщо Т – період, то пТ – період, де ![]() ,
, ![]() . Звичайно, говорячи про період, мають на увазі найменший додатний період, який називається основним.
. Звичайно, говорячи про період, мають на увазі найменший додатний період, який називається основним.
Основними періодами для тригонометричних функцій є: ![]() для функцій
для функцій ![]() ,
, ![]() ;
; ![]() для функцій
для функцій ![]() ,
, ![]() .
.
У більш загальному вигляді можемо записати:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Якщо кути виражаються в радіанах, то:
![]() – основний період функцій
– основний період функцій ![]() ,
, ![]() ;
;
![]() – основний період функцій
– основний період функцій ![]() ,
, ![]() .
.
Відомо, що періоди функцій
![]() і
і ![]()
обчислюються за формулою 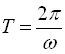 ,
,
а періоди функцій ![]() і
і ![]()
обчислюються за формулою 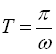 .
.
Якщо період функції ![]() дорівнює
дорівнює ![]() , а період функції
, а період функції ![]() дорівнює
дорівнює ![]() , то період функції
, то період функції ![]()
і ![]() дорівнює найменшому числу, при діленні якого на
дорівнює найменшому числу, при діленні якого на ![]() і
і ![]() дістаємо цілі числа.
дістаємо цілі числа.
Приклад 20
Знайти період функції: а) 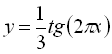 ; б)
; б) ![]() ;
;
в) 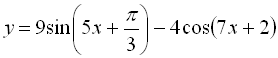 .
.
Розв’язання:
а) Період функції 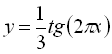 дорівнює
дорівнює 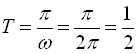 .
.
б) Для того, щоб знайти період функції ![]() , потрібно застосувати формули пониження степеня:
, потрібно застосувати формули пониження степеня: 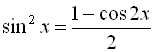 , тобто
, тобто 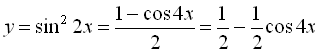 .
.
Період функції 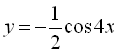 , а отже і даної функції
, а отже і даної функції ![]() є число
є число 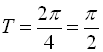 .
.
в) Знаходимо періоди доданків.
Період функції 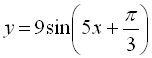 дорівнює
дорівнює 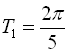 ,
,
а період функції ![]() дорівнює
дорівнює 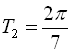 .
.
Очевидно, що період заданої функції дорівнює ![]() .
.
1.10. Властивості функцій ![]() і
і ![]() та їх графіки
та їх графіки
Таблиця 2
Властивості функцій ![]() і
і ![]()
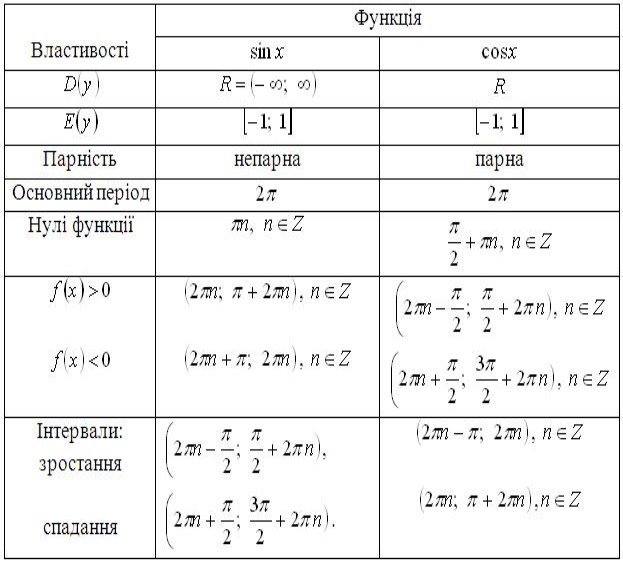
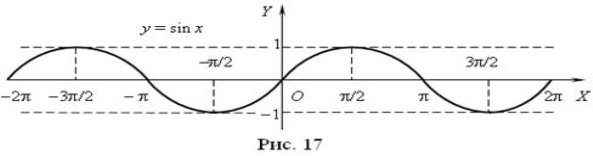
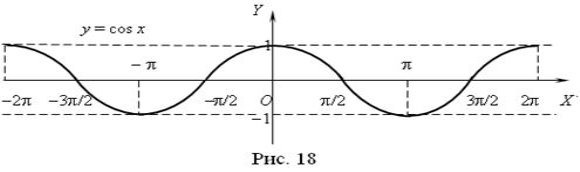
Графік функції ![]() називається синусоїдою (рис. 17), а графік функції
називається синусоїдою (рис. 17), а графік функції ![]() – косинусоїдою (рис. 18).
– косинусоїдою (рис. 18).
1.11. Властивості функцій ![]() і
і ![]() та їх графіки
та їх графіки
Таблиця 3
Властивості функцій ![]() і
і ![]()

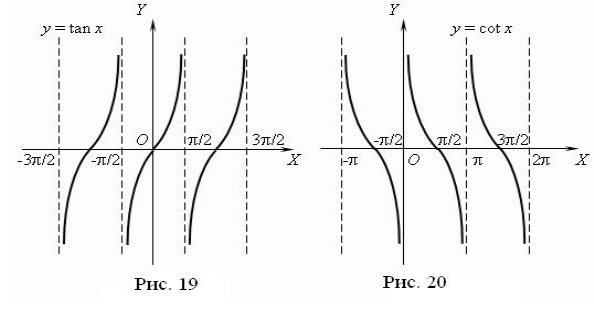
Графік функції ![]() називається тангенсоїдою (рис. 19), а графік функції
називається тангенсоїдою (рис. 19), а графік функції ![]() – котангенсоїдою (рис. 20).
– котангенсоїдою (рис. 20).
1.12. Поняття оборотної та оберненої функцій
Функція, яка приймає кожне своє значення в єдиній точці області визначення, є оборотною.
У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає.
Інакше кажучи, якщо функція ![]() є оборотною й число а належить до її області значень
є оборотною й число а належить до її області значень ![]() , то рівняння
, то рівняння ![]() має розв’язок, причому єдиний.
має розв’язок, причому єдиний.
Оберненою до даної оборотної функції ![]() називається така функція
називається така функція ![]() , яка кожному із множини значень функції
, яка кожному із множини значень функції ![]() ставить у відповідність єдине число x з області визначення.
ставить у відповідність єдине число x з області визначення.
Функції, обернені функціям ![]() ,
, ![]() ,
, ![]() ,
, ![]() на відповідних інтервалах, називаються оберненими тригонометричними.
на відповідних інтервалах, називаються оберненими тригонометричними.
Вони позначаються ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Тригонометричні функції ![]() ,
, ![]() не є монотонними у всій області їх визначення. Тому для утворення обернених функцій виділяють інтервали монотонності.
не є монотонними у всій області їх визначення. Тому для утворення обернених функцій виділяють інтервали монотонності.
1.12.1. Функція ![]() та її графік
та її графік
Функція ![]() на відрізку
на відрізку 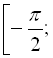
![]() зростає і набуває всіх значень з відрізка
зростає і набуває всіх значень з відрізка ![]()
![]() . Тому функція
. Тому функція ![]() на відрізку
на відрізку 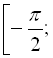
![]() оборотна, тобто має обернену функцію, що називається арксинусом і позначається
оборотна, тобто має обернену функцію, що називається арксинусом і позначається ![]() . Таким чином, арксинусом числа х називається число
. Таким чином, арксинусом числа х називається число ![]() з відрізка
з відрізка 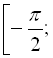
![]() таке, що його синус дорівнює х. Математично це можна записати так:
таке, що його синус дорівнює х. Математично це можна записати так: ![]()
![]()
![]() ,
,
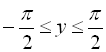 ,
, ![]() .
.
Наприклад, 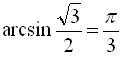
(оскільки 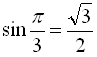 ,
, 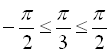 ),
), ![]() ,
,
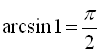 ,
, 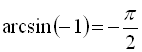 .
.
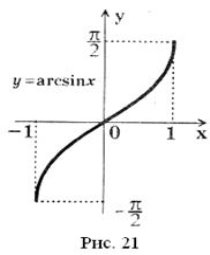
Графік функції ![]() , який зображений на рисунку 21, симетричний графіку функції
, який зображений на рисунку 21, симетричний графіку функції ![]() ,
, 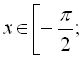
![]() відносно прямої
відносно прямої ![]() .
.
Основні властивості функції ![]()
1) ![]()
![]() .
.
2) 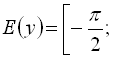
![]() .
.
3) ![]() , тобто
, тобто ![]() – непарна функція.
– непарна функція.
4) Функція зростаюча.
5) ![]() при
при ![]() .
.
Функція ![]() на відрізку
на відрізку ![]()
![]() спадає і набуває всіх значень з відрізка
спадає і набуває всіх значень з відрізка ![]()
![]() . Тому функція
. Тому функція ![]() на відрізку
на відрізку ![]()
![]() оборотна, тобто має обернену функцію, що називається арккосинусом і позначається
оборотна, тобто має обернену функцію, що називається арккосинусом і позначається ![]() . Таким чином, арккосинусом числа х називається число
. Таким чином, арккосинусом числа х називається число ![]() з відрізка
з відрізка ![]()
![]() таке, що його косинус дорівнює х. Математично це можна записати так:
таке, що його косинус дорівнює х. Математично це можна записати так: ![]()
![]()
![]() ,
, ![]() ,
, ![]() .
.
Наприклад, 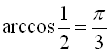 (оскільки
(оскільки 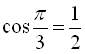 ,
, 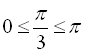 ),
),
![]() ,
, ![]() і т.д.
і т.д.
Графік функції зображено на рисунку 22. Цей графік симетричний графіку функції ![]() відносно прямої
відносно прямої ![]() .
.
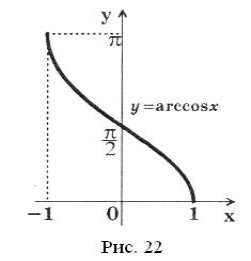
Основні властивості функції ![]()
-
-
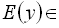
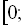
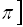
-
функція
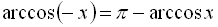 є функцією загального виду.
є функцією загального виду.
4) Функція є спадною.
1.12.3. Функція ![]() та її графік
та її графік
Функція ![]() на інтервалі
на інтервалі ![]()
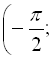
![]() зростає і набуває всіх числових значень .
зростає і набуває всіх числових значень .
Тому функція ![]() оборотна, тобто має обернену функцію, що називається арктангенсом .
оборотна, тобто має обернену функцію, що називається арктангенсом .
Таким чином, арктангенсом числа х називається число ![]() з інтервалу
з інтервалу 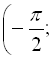
![]() таке, що його тангенс дорівнює х. Математично це можна записати так:
таке, що його тангенс дорівнює х. Математично це можна записати так: ![]()
![]() ,
, ![]() ,
, 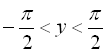 .
.
Наприклад, ![]()
(оскільки 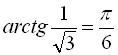 ,
, 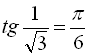 ),
),
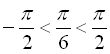 ,
, 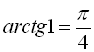 ,
, ![]() і т.д.
і т.д.
Графік функції 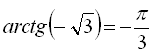 зображений на рисунку 23. Цей графік симетричний графіку функції
зображений на рисунку 23. Цей графік симетричний графіку функції ![]() ,
, ![]()
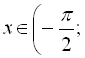
![]() , відносно прямої .
, відносно прямої .
1) 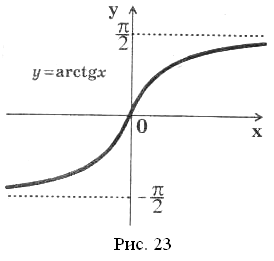 .
.
Основні властивості функції ![]()
2) ![]()
![]() .
.
3) 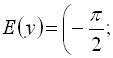
![]() дана функція є непарною.
дана функція є непарною.
4) Функція є зростаючою.
5) ![]() при
при ![]()
![]() .
.
Функція ![]() на інтервалі
на інтервалі ![]()
![]() спадає і набуває усіх числових значень, оскільки .
спадає і набуває усіх числових значень, оскільки .
Тому функція ![]() оборотна, тобто має обернену функцію, що називається арккотангенсом і позначається .
оборотна, тобто має обернену функцію, що називається арккотангенсом і позначається .
Таким чином, арккотангенсом числа х називається число ![]() з інтервалу
з інтервалу![]()
![]() таке, що його котангенс дорівнює х. Математично це можна записати так:
таке, що його котангенс дорівнює х. Математично це можна записати так: ![]() ,
, ![]() ,
, ![]() .
.
Наприклад, ![]() (оскільки
(оскільки ![]() ,
, 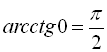 ),
),
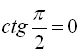 ,
, 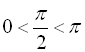 ,
, 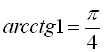 і т.д.
і т.д.
Графік функції 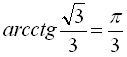 зображено на рисунку 24. Цей графік симетричний графіку функції
зображено на рисунку 24. Цей графік симетричний графіку функції 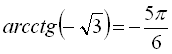 відносно прямої .
відносно прямої .
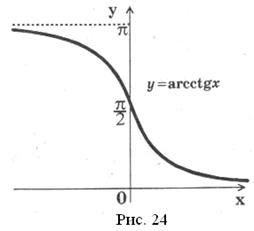
Основні властивості функції ![]()
1) ![]()
![]() .
.
2) ![]()
![]()
![]() .
.
3) функція є функцією загального виду.
4) Функція спадна.
5) ![]() при
при ![]()
![]() .
.
Виходячи з означення тригонометричних функцій, запишемо декілька співвідношень між цими функціями:
при ![]()
![]()
![]() ,
, ![]() ,
, 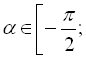
![]()
![]()
![]() ,
,
для кутів ![]()
![]()
![]() ;
; ![]() .
.
Аналогічні співвідношення зв’язують ![]() і
і ![]() :
:
для всіх ![]()
![]() ;
; ![]() ,
,
для всіх 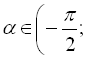
![]()
![]() ,
,
для всіх ![]()
![]()
![]() .
.
1.13. Приклади перетворень виразів, що містять обернені тригонометричні функції
Приклад 21
Спростити вираз ![]() , де
, де ![]() .
.
Розв’язання:
Припустимо, ![]() . Тоді
. Тоді ![]() ,
, ![]() .
.
Треба знайти ![]() . Відомо, що
. Відомо, що ![]() ,
, ![]() , а на відрізку
, а на відрізку ![]()
![]() синус набуває лише невід’ємного значення. Тому
синус набуває лише невід’ємного значення. Тому ![]() , тобто
, тобто ![]() .
.
Приклад 22
Обчислити 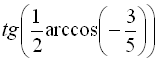 .
.
Розв’язання:
Припустимо 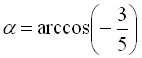 . Тоді
. Тоді 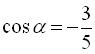 ,
, 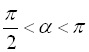 .
.
Треба обчислити ![]() .
.
Маємо 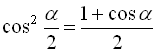 , значить
, значить 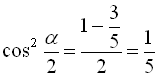 .
.
Оскільки далі 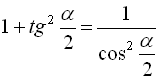 , то
, то 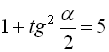 , звідки
, звідки 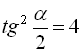 , тобто
, тобто 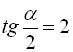 або
або 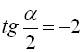 .
.
За умовою 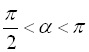 означає
означає 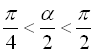 , а в інтервалі
, а в інтервалі ![]()
![]() маємо
маємо 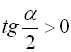 .
.
Отже, 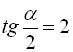 , тобто
, тобто 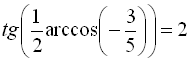 .
.
Відповідь: 2.
Приклад 23
Обчислити 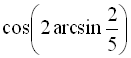 .
.
Розв’язання:
Припустимо, 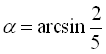 . Тоді
. Тоді 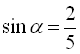 ,
, 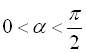 .
.
Потрібно обчислити ![]() . Виразимо формулу косинуса подвійного кута через синус кута:
. Виразимо формулу косинуса подвійного кута через синус кута: ![]() .
.
Тоді, підставляючи значення ![]() , будемо мати
, будемо мати 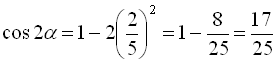 . Отже,
. Отже, 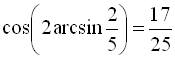 .
.
Відповідь: ![]() .
.
Приклад 24
Обчислити 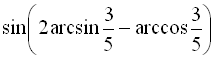 .
.
Розв’язання:
Позначимо 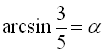 , а
, а 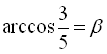 , тоді
, тоді 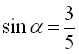 ,
, 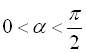 , а
, а
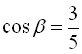 ,
, 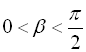 . Потрібно обчислити
. Потрібно обчислити ![]() . Для цього скористаємося формулою (18), отже
. Для цього скористаємося формулою (18), отже
![]() . (*)
. (*)
Згідно з формулою (21) маємо ![]() .
.
Знайдемо ![]() :
: ![]() , тобто
, тобто 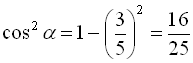 , то
, то 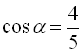 або
або 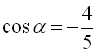 . За умовою
. За умовою 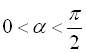 маємо, що
маємо, що ![]() . Тобто
. Тобто 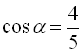 , а отже
, а отже 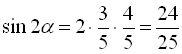 .
.
![]() будемо шукати як у попередньому прикладі, тобто
будемо шукати як у попередньому прикладі, тобто 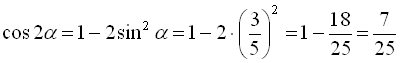 . Значить,
. Значить, 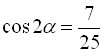 .
.
Знайдемо ![]() з формули
з формули ![]() , підставляючи
, підставляючи 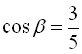
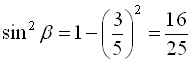 ,
, 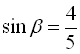 або
або 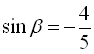 .
.
За умовою 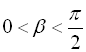 маємо, що
маємо, що ![]() , тобто
, тобто 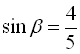 .
.
Знайдені значення підставимо у рівність (*):
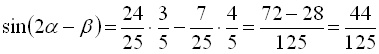 .
.
Відповідь: ![]() .
.
1.14. Побудова графіків тригонометричних функцій
Приклад 25
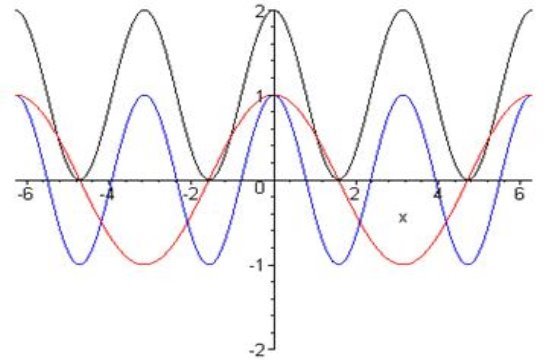
Побудувати графік функції ![]() .
.
Розв’язання:
Шляхом елементарних перетворень будуємо графіки таких функцій:
1) ![]() ;
;
2) ![]() (стиснути графік
(стиснути графік ![]() вздовж осі
вздовж осі ![]() до осі
до осі ![]() у 2 рази);
у 2 рази);
3) ![]() (зсунути графік
(зсунути графік![]() вздовж осі
вздовж осі ![]() на 1 одиницю вгору).
на 1 одиницю вгору).
Приклад 26
Побудувати графік функції 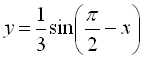 .
.
Розв’язання:
І спосіб: Перетворимо 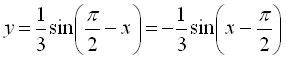 .
.
Шляхом елементарних перетворень будуємо графіки таких функцій:
1) ![]() ;
;
2) 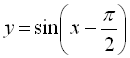 (зсуваємо графік
(зсуваємо графік ![]() на
на ![]() вправо вздовж осі
вправо вздовж осі ![]() );
);
3) 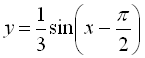 (стискаємо графік
(стискаємо графік 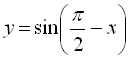 до осі
до осі ![]() у 3 рази);
у 3 рази);
4) 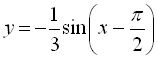 (перевертаємо графік
(перевертаємо графік 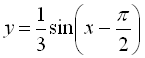 відносно осі
відносно осі ![]() ).
).
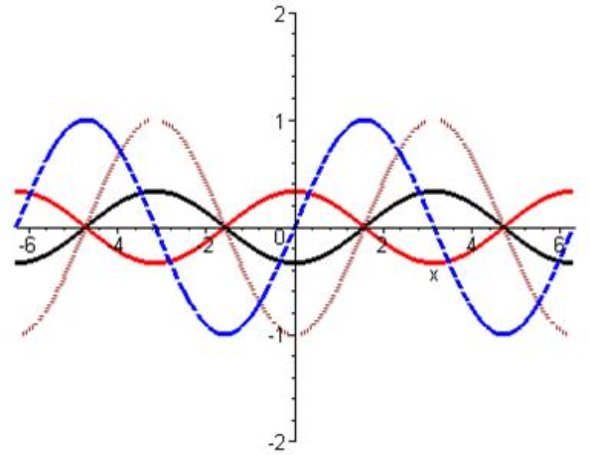
ІІ спосіб: Перетворимо функцію 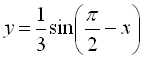 за допомогою фор-
за допомогою фор-
мул зведення: 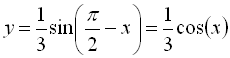 .
.
Приклад 27
Побудувати графік функції ![]() .
.
Розв’язання:
Спочатку будуємо графік функції ![]() . Для того, щоб утворився графік функції
. Для того, щоб утворився графік функції ![]() , потрібно ту частину графіка
, потрібно ту частину графіка ![]() , яка вище осі
, яка вище осі ![]() , залишити без змін, а ту, що нижче осі
, залишити без змін, а ту, що нижче осі ![]() , симетрично відобразити на верхню півплощину.
, симетрично відобразити на верхню півплощину.
Приклад 28
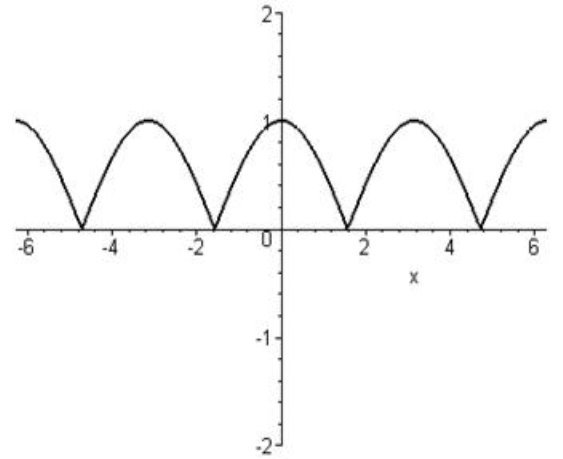
Побудувати графік функції ![]() .
.
Розв’язання:
Будуємо графік функції ![]() . Ту частину побудованого графіка, яка в лівій півплощині відносно осі OY, відкидаємо, а ту, що в правій, – залишаємо і симетрично відображаємо на ліву півплощину.
. Ту частину побудованого графіка, яка в лівій півплощині відносно осі OY, відкидаємо, а ту, що в правій, – залишаємо і симетрично відображаємо на ліву півплощину.
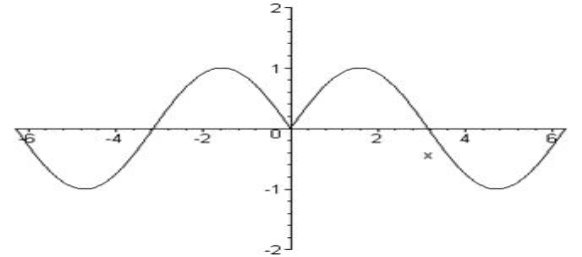
Приклад 29
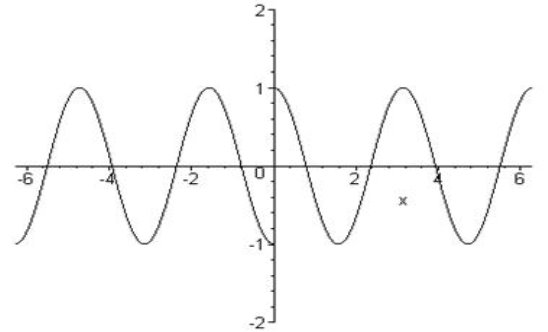
Побудувати графік функції 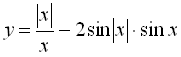 .
.
Розв’язання
![]()
![]()
![]() .
.
Оскільки підмодулевий вираз це х, то розглянемо два випадки:
Якщо ![]() :
: 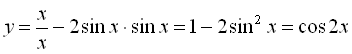 .
.
Якщо ![]() :
: 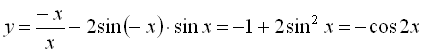 .
.
Шляхом елементарних перетворень будуємо відповідні графіки функцій.
1.15. Тренувальні вправи
Завдання 1. У яких координатних чвертях закінчуються кути:
1. 80? і -80?; 3. 300? і -300?; 5. 1000? і -1000?;
2. 170? і -170?; 4. 250? і -250?; 6. 5200? і -5200?.
Завдання 2. Виразити в радіанах дані кути:
1. 20?; 4. 240?; 7. 135?;
2. 50?; 5. 330?; 8. 315?;
3. 150?; 6. 210?; 9. 120?.
Завдання 3. Виразити в градусах дані кути:
1. ![]() 3.
3. ![]() 5.
5. ![]()
2. 3π; 4. ![]() 6.
6. ![]()
Завдання 4. Визначити знак виразу без використання таблиць і калькулятора.
1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() .
.
Завдання 5. Обчислити без використання таблиць і калькулятора значення тригонометричних виразів.
1. ![]() ; 3.
; 3. 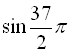 ; 5.
; 5. ![]() ;
;
2. ![]() ; 4.
; 4. 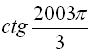 ; 6.
; 6. 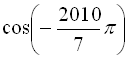 .
.
Завдання 6. Знайти значення інших тригонометричних функцій кута ![]() за такими даними:
за такими даними:
1. ![]() при
при ![]() ; 3.
; 3. ![]() при
при 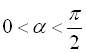 ;
;
2. ![]() при
при 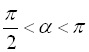 ; 4.
; 4. ![]() при
при ![]() .
.
Завдання 7. Обчислити значення виразу.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() , якщо
, якщо ![]() ;
;
5. 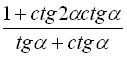 , якщо
, якщо 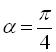 ;
;
6. ![]() , якщо
, якщо 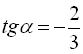 ;
;
7. ![]() , якщо
, якщо ![]() ;
;
8. ![]() , якщо
, якщо 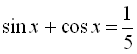 ;
;
9. 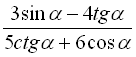 , якщо
, якщо 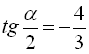 ,
, 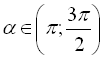 ;
;
10. 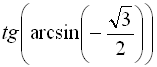 ;
;
11. 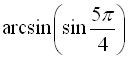 ;
;
12. 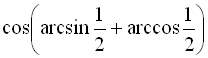 ;
;
13. 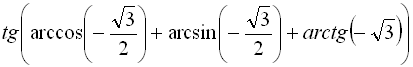 ;
;
14. 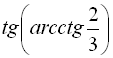 ;
;
15. ![]() ;
;
16. 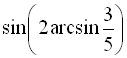 ;
;
17. 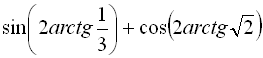 .
.
Завдання 8. Довести тотожності.
1. ![]() ;
;
2. 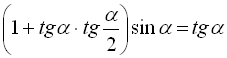 ;
;
3. ![]() ;
;
4. 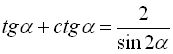 ;
;
5. 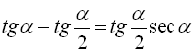 ;
;
6. 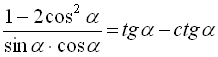 ;
;
7. ![]() ;
;
8. 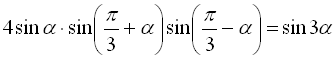 ;
;
9. ![]() ;
;
10. ![]() ;
;
11. ![]() ;
;
12. 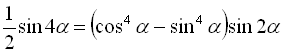 ;
;
13. 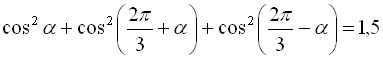 ;
;
14. ![]() ;
;
15. ![]() ;
;
16. 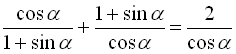 ;
;
17. 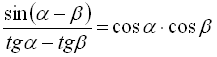 ;
;
18. 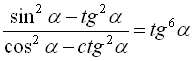 ;
;
19. 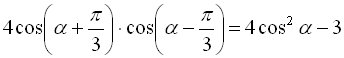 ;
;
20. ![]() .
.
Завдання 9. Спростити вирази.
1. ![]() ;
;
2. ![]() ;
;
3. 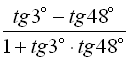 ;
;
4. 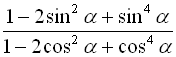 ;
;
5. ![]() ;
;
6. ![]() ;
;
7. 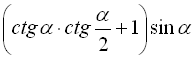 ;
;
8. 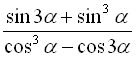 ;
;
9. 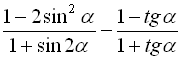 ;
;
10. 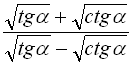 ;
;
11. 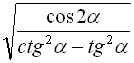 ,
, ![]() ;
;
12. 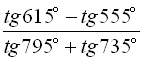 ;
;
13. 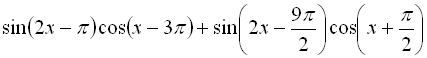 ;
;
14. ![]() .
.
Завдання 10. Перетворити у добуток.
1. ![]() ;
;
2. ![]() ;
;
3. 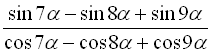 ;
;
4. ![]() ;
;
5. ![]() .
.
Завдання 11. Дослідити функції на парність (непарність).
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. 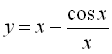 .
.
Завдання 12. Знайти основний період функції.
1. 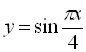 ;
;
2. 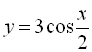 ;
;
3. 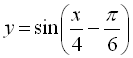 ;
;
4. 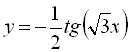 ;
;
5. ![]() ;
;
6. ![]() ;
;
7. 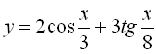 ;
;
8. 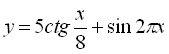 ;
;
9. ![]() ;
;
10. ![]() .
.
Завдання 13. Побудувати графік функції.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. ![]() ;
;
8. 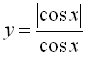 ;
;
9. ![]() ;
;
10. ![]() ;
;
11. 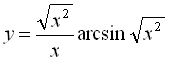 ;
;
12. ![]() .
.
2. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
2.1. Найпростіші тригонометричні рівняння
Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення ![]() тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
![]() ,
, ![]() (оскільки
(оскільки ![]() ). Корені рівняння
). Корені рівняння ![]() можна розглядати як абсциси точок перетину синусоїди
можна розглядати як абсциси точок перетину синусоїди ![]() з прямою
з прямою ![]() .
.
Всі розв’язки рівняння ![]() записуються у вигляді
записуються у вигляді ![]() ,
, ![]() . Однак в трьох таких випадках, коли
. Однак в трьох таких випадках, коли![]()
![]()
![]() , розв’язки рівнянь зображуються такими формулами:
, розв’язки рівнянь зображуються такими формулами:
при ![]()
![]() ,
, ![]() ;
;
при ![]()
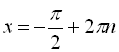 ,
, ![]() ;
;
при ![]()
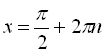 ,
, ![]() .
.
Рівняння ![]() . Оскільки
. Оскільки ![]() , то рівняння має розв’язок тільки при
, то рівняння має розв’язок тільки при ![]() . Корені рівняння
. Корені рівняння ![]() можна розглядати як абсциси точок перетину косинусоїди
можна розглядати як абсциси точок перетину косинусоїди ![]() з прямою
з прямою ![]() .
.
Всі розв’язки рівняння
![]() записуються у вигляді
записуються у вигляді ![]() ,
, ![]() .
.
Для окремих випадків ![]() ,
, ![]() маємо:
маємо:
а) ![]()
![]()
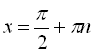 ,
, ![]() ;
;
б) ![]()
![]()
![]() ,
, ![]() ;
;
в) ![]()
![]()
![]() ,
, ![]() .
.
Всі корені рівняння
![]() ,
, ![]() задаються формулою
задаються формулою ![]() ,
, ![]() .
.
У випадку ![]() розв’язок записується у вигляді
розв’язок записується у вигляді ![]() ,
, ![]() .
.
Всі корені рівняння
![]() ,
, ![]() визначаються співвідношенням
визначаються співвідношенням ![]() ,
,![]()
При ![]() розв’язок має вигляд
розв’язок має вигляд 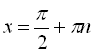 ,
, ![]() .
.
При використанні формул для розв’язування тригонометричних рівнянь враховують, що
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Розглянемо на прикладах найпростіші тригонометричні рівняння.
Приклад 1
Розв’язати рівняння 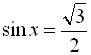 .
.
Розв’язання:
Оскільки 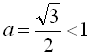 , то скористаємось формулою
, то скористаємось формулою ![]() ,
, ![]() .
.
Отже, 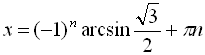 ,
, ![]()
![]()
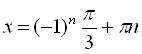 ,
, ![]() .
.
Відповідь: 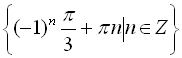 .
.
Приклад 2
Розв’язати рівняння 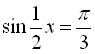 .
.
Розв’язання:
![]() (
(![]() ), отже, рівняння розв’язків не має.
), отже, рівняння розв’язків не має.
Відповідь: ![]() .
.
Приклад 3
Розв’язати рівняння 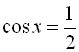 .
.
Розв’язання:
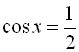
![]()
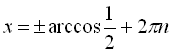 ,
, ![]()
![]()
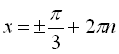 ,
, ![]() .
.
Відповідь: 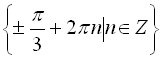 .
.
Приклад 4
Розв’язати рівняння 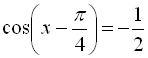 .
.
Розв’язання:
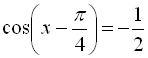
![]()
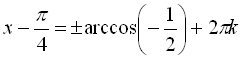 ,
, ![]()
![]()
![]()
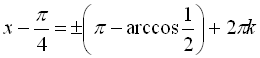 ,
,![]()
![]()
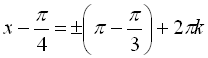 ,
, ![]()
![]()
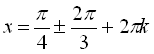 ,
, ![]()
![]()
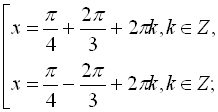
![]()
![]()
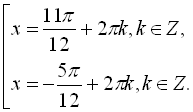
Відповідь: 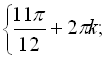
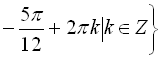 .
.
Приклад 5
Розв’язати рівняння 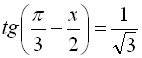 .
.
Розв’язання:
Запишемо дане рівняння у вигляді 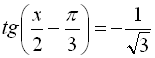 , тоді скористаємось формулою
, тоді скористаємось формулою ![]() ,
, ![]() , тобто
, тобто 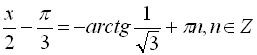
![]()
![]()
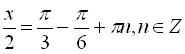
![]()
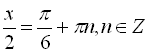
![]()
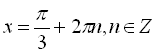 .
.
Відповідь: 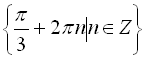 .
.
Приклад 6
Розв’язати рівняння 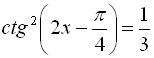 .
.
Розв’язання:
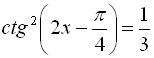
![]()
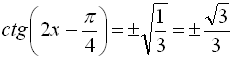
![]()
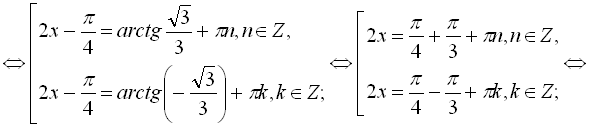
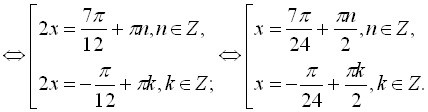
Відповідь: 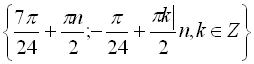 .
.
Відзначимо, що при ![]() ,
, ![]() загальними формулами для тригонометричних рівнянь також можна користуватися, вони дають правильний результат, однак найчастіше ці формули не мають компактного вигляду. Наприклад, якщо використовувати окремі випадки, то
загальними формулами для тригонометричних рівнянь також можна користуватися, вони дають правильний результат, однак найчастіше ці формули не мають компактного вигляду. Наприклад, якщо використовувати окремі випадки, то ![]()
![]()
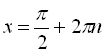 ,
, ![]() . Якщо ж скористатися спільною формулою, то
. Якщо ж скористатися спільною формулою, то ![]()
![]()
![]() ,
, ![]() .
.
Покажемо, що 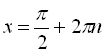 ,
, ![]() і
і ![]() ,
, ![]() – це та сама множина.
– це та сама множина.
Дійсно, при ![]()
![]()
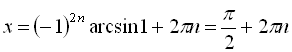 ,
, ![]() ; при
; при ![]()
![]()
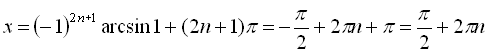 ,
, ![]() .
.
Таким чином, множини розв’язків, отримані двома способами, збігаються.
Зауваження
При розв’язуванні тригонометричних рівнянь з однаковим успіхом можна користуватися і радіанною, і градусною мірами. Так, наприклад, відповідь у прикладі № 5, яка записана за допомогою радіанної міри 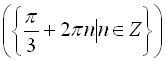 , можна записати, використовуючи градусну міру, так:
, можна записати, використовуючи градусну міру, так: 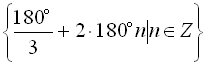
![]()
![]() . При цьому слід знати, що можна використовувати або тільки радіанну, або тільки градусну міру, тобто не можна використовувати в тому самому розв’язку частково радіанну і частково градусну міру.
. При цьому слід знати, що можна використовувати або тільки радіанну, або тільки градусну міру, тобто не можна використовувати в тому самому розв’язку частково радіанну і частково градусну міру.
Приклад 8
Вказати найменший додатний розв’язок рівняння (у градусах): 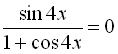 .
.
Розв’язання:
Дане рівняння є дробово-раціональним, тому його можна записати у вигляді системи: 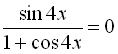
![]()
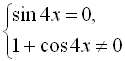
![]()
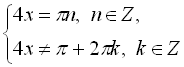
![]()
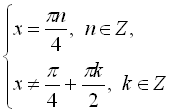 . Звідси
. Звідси 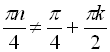
![]()
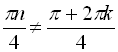
![]()
![]() , тобто підходить лише
, тобто підходить лише ![]() . Таким чином,
. Таким чином, 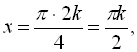
![]() .
.
Найменший додатний розв’язок рівняння при ![]() буде
буде 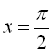 або
або ![]() .
.
Відповідь: ![]() .
.
2.2. Загальний принцип розв’язування тригонометричних рівнянь
Цей принцип полягає в тому, що всі тригонометричні функції, які входять в рівняння, виражають через яку-небудь одну тригонометричну функцію, яка залежить від одного і того ж аргументу. Розглянемо даний принцип на прикладах:
Приклад 9
Розв’язати рівняння ![]() .
.
Розв’язання:
Замінивши ![]() на
на ![]() ,
,
отримаємо ![]()
![]()
![]()
![]() .
.
Замінимо ![]() через
через ![]() :
: ![]()
![]()
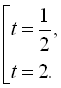
Повертаючись до заміни, отримаємо 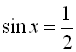 або
або ![]() .
.
Перше рівняння системи є найпростішим тригонометричним і його розв’язком буде 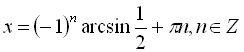
![]()
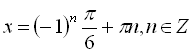 . У другому рівнянні системи права його частина
. У другому рівнянні системи права його частина ![]() , тому рівняння
, тому рівняння ![]() розв’язків не має.
розв’язків не має.
Відповідь: 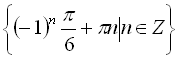 .
.
Приклад 10
Розв’язати рівняння 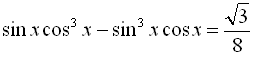 .
.
Розв’язання:
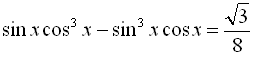
![]()
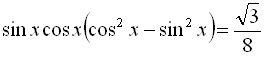
![]()
![]()
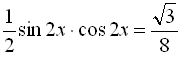
![]()
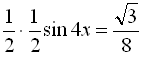
![]()
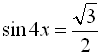
![]()
![]()
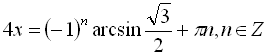
![]()
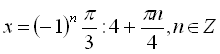
![]()
![]()
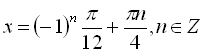 .
.
Відповідь: 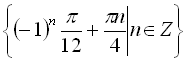 .
.
2.3. Розв’язування тригонометричних рівнянь методом групування
Шляхом групування доданків рівняння зводяться до вигляду, коли ліва частина розкладена на множники, а права рівна нулю.
Приклад 11
Розв’язати рівняння
![]() .
.
Розв’язання:
Згрупуємо доданки в лівій і правій частинах рівняння: ![]() . За формулою перетворення суми синусів, а також за формулою косинуса подвійного кута, отримаємо
. За формулою перетворення суми синусів, а також за формулою косинуса подвійного кута, отримаємо ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Звідси
. Звідси 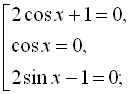
![]()
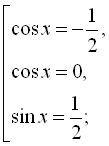
![]()
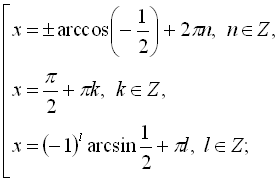
![]()
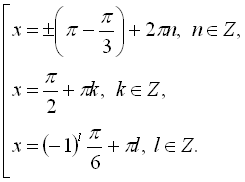
Відповідь: 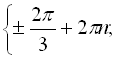
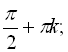
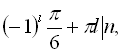
![]()
![]() .
.
Приклад 12
Розв’язати рівняння 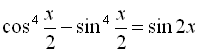 .
.
Розв’язання:
За формулою різниці квадратів розпишемо ліву частину рівняння 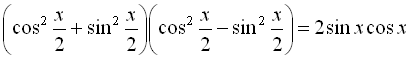
![]()
![]()
![]()
![]()
![]()
![]()
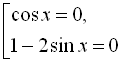
![]()
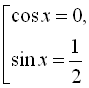
![]()
![]()
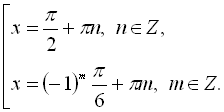
Відповідь: 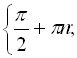
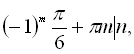
![]() .
.
2.4. Рівняння, які розв’язуються пониженням степеня
Якщо тригонометричні рівняння містять ![]() ,
, ![]() в парному степені, то застосовують формули пониження степеня:
в парному степені, то застосовують формули пониження степеня:
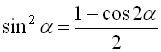 ,
, 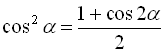 .
.
Приклад 13
Розв’язати рівняння ![]() .
.
Розв’язання:
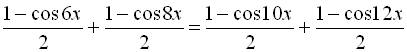
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Кожний множник отриманого рівняння прирівнюємо до нуля і знаходимо його корені: ![]()
![]()
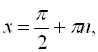
![]() ;
; ![]()
![]()
![]()
![]()
![]()
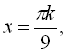
![]()
![]()
![]()
![]()
![]()
![]()
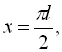
![]() .
.
Відповідь: 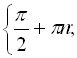
![]()
![]()
![]()
![]() .
.
2.5. Розв’язування однорідних тригонометричних рівнянь, а також рівнянь, які зводяться до однорідних тригонометричних
Однорідні тригонометричні рівняння – це рівняння виду
![]() (1)
(1)
і ![]() . (2)
. (2)
Розв’язуються вони шляхом ділення обох частин рівняння на ![]() для рівняння виду (1) і на
для рівняння виду (1) і на ![]() для рівняння виду (2).
для рівняння виду (2).
Приклад 14
Розв’язати рівняння ![]() .
.
Розв’язання:
Поділимо обидві частини рівняння на ![]()
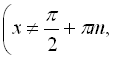
![]() :
:
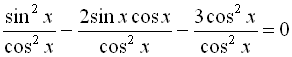
![]()
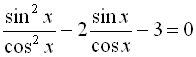
![]()
![]()
![]()
![]()
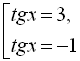
![]()
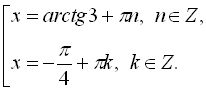
Перевіримо, чи 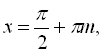
![]() не є коренем початкового рівняння:
не є коренем початкового рівняння: 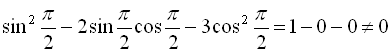 . Отже
. Отже 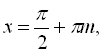
![]() не є коренем нашого рівняння.
не є коренем нашого рівняння.
Відповідь: ![]()
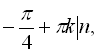
![]() .
.
Приклад 15
Розв’язати рівняння ![]() .
.
Розв’язання:
![]()
![]()
![]()
![]()
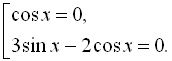
Розв’яжемо перше рівняння сукупності: ![]()
![]()
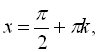
![]() .
.
Друге рівняння сукупності є однорідним тригонометричним, тому поділимо обидві частини рівняння ![]() на
на ![]()
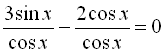
![]()
![]()
![]()
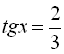
![]()
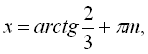
![]() .
.
Оскільки права частина рівняння дорівнює нулю, а ліву частину розглянути як функцію, то графічно розв’язками рівняння будуть абсциси точок перетину графіка функції ![]() з віссю ОХ.
з віссю ОХ.
Відповідь: 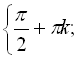
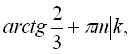
![]() .
.
2.6. Розв’язування тригонометричних рівнянь за допомогою універсальної підстановки 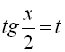
При розв’язуванні рівнянь виду ![]() зручно застосову-вати універсальну підстановку
зручно застосову-вати універсальну підстановку 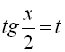 . Тоді функції
. Тоді функції ![]() ,
, ![]() нескладно виражаються через
нескладно виражаються через 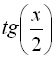 за такими формулами:
за такими формулами:
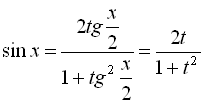 ,
, 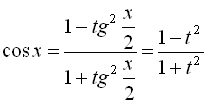 .
.
Оскільки використання універсальної підстановки можливе лише при ![]()
![]() , то потрібно перевіряти, чи не є числа виду
, то потрібно перевіряти, чи не є числа виду ![]()
![]() розв’язками початкового рівняння.
розв’язками початкового рівняння.
Приклад 16
Розв’язати рівняння ![]() .
.
Розв’язання:
Зробимо підстановку 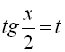 ,
, 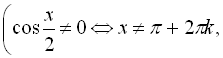
![]() .
.
Тоді 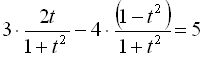
![]()
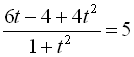
![]()
![]()
![]()
![]() .
.
Значить 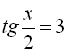
![]()
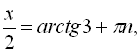
![]()
![]()
![]()
![]() .
.
Перевіримо, чи не є розв’язком даного рівняння ![]()
![]() ,
, ![]() .
.
Відповідь: ![]() .
.
Приклад 17
Розв’язати рівняння ![]() .
.
Розв’язання:
Можна замінити ![]() через х, а потім зробити підстановку
через х, а потім зробити підстановку 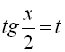 ,
,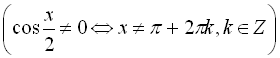 . Тоді
. Тоді 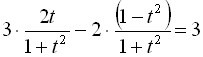
![]()
![]()
![]()
![]() або
або ![]() . Повернувшись до підстановки
. Повернувшись до підстановки 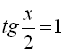 (а) або
(а) або 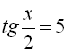 (б), розв’яжемо по черзі рівняння (а) і (б):
(б), розв’яжемо по черзі рівняння (а) і (б):
(а): 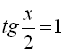
![]()
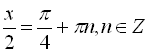
![]()
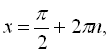
![]()
![]()
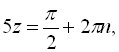
![]()
![]()
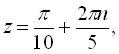
![]() ;
;
(б): 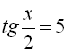
![]()
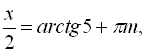
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
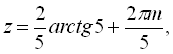
![]() .
.
Перевіримо, чи не є розв’язком даного рівняння ![]()
![]() :
:![]() .
.
Відповідь: 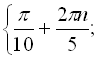
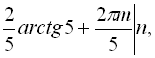
![]() .
.
2.7. Метод введення допоміжного кута
Іноді при розв’язуванні тригонометричних рівнянь корисно скористатися формулою ![]() ,
,
де 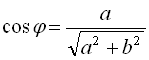 ,
, 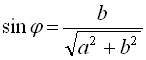 .
.
У цьому випадку ![]() називається допоміжним аргументом або допоміжним кутом.
називається допоміжним аргументом або допоміжним кутом.
Сенс методу полягає в тому, що деяку величину подають як тригонометричну функцію відповідного аргументу ![]() , а потім роблять тригонометричні перетворення.
, а потім роблять тригонометричні перетворення.
Приклад 18
Розв’язати рівняння 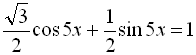 .
.
Розв’язання:
1-й спосіб:
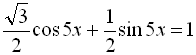
![]()
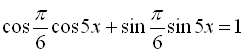
![]()
![]()
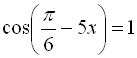
![]()
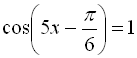
![]()
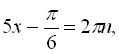
![]()
![]()
![]()
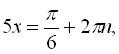
![]()
![]()
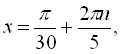
![]() .
.
У процесі розв’язування ми врахували той факт,
що якщо 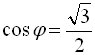 ,
, 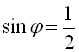 , то
, то ![]() можна покласти таким, що дорівнює
можна покласти таким, що дорівнює ![]() .
.
2-й спосіб:
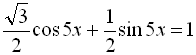
![]()
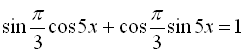
![]()
![]()
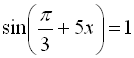
![]()
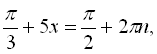
![]()
![]()
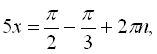
![]()
![]()
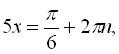
![]()
![]()
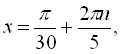
![]() .
.
Відповідь: 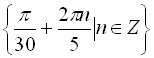 .
.
Приклад 19
Розв’язати рівняння ![]() .
.
Розв’язання:
Оскільки ![]() , то поділимо обидві частини нашого рівняння на 2 і введемо допоміжний кут:
, то поділимо обидві частини нашого рівняння на 2 і введемо допоміжний кут: 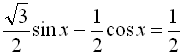
![]()
![]()
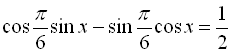
![]()
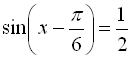
![]()
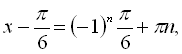
![]()
![]()
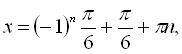
![]() . Даний розв’язок можна розписати як
. Даний розв’язок можна розписати як 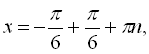
![]()
![]()
![]()
![]() , якщо п – непарне або
, якщо п – непарне або 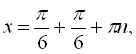
![]()
![]()
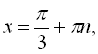
![]() , якщо п – парне.
, якщо п – парне.
Відповідь: 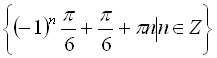 .
.
2.8. Розв’язування тригонометричних рівнянь способом підстановки
У деяких раніше розглянутих рівняннях застосовувалася заміна змінної, коли ці рівняння зводилися до алгебраїчних відносно однієї з тригонометричних функцій. Розглянемо більш складні випадки заміни змінних.
Приклад 20
Розв’язати рівняння 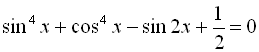 .
.
Розв’язання:
Скористаємося формулою ![]() , тоді
, тоді 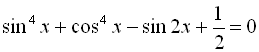
![]()
![]()
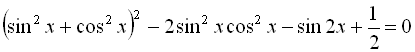
![]()
![]()
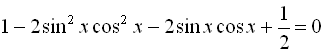
![]()
![]()
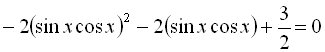 . Зробимо заміну
. Зробимо заміну ![]() :
:
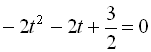
![]()
![]()
![]()
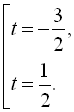 Повернемось до заміни:
Повернемось до заміни:
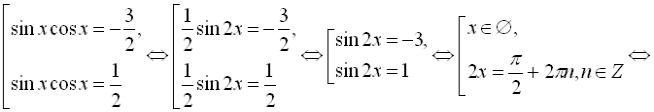
![]()
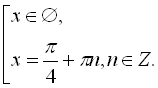 Відповідь:
Відповідь: 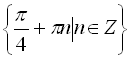 .
.
Приклад 21
Розв’язати рівняння ![]() .
.
Розв’язання:
Позначивши ![]() , дістанемо
, дістанемо ![]()
![]()
![]()
![]() .
.
Тоді початкове рівняння запишеться у вигляді ![]()
![]()
![]()
![]()
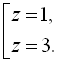 Повернемось до заміни:
Повернемось до заміни:
![]() (1)
(1)
або ![]() . (2)
. (2)
Найпростішим методом розв’язування рівняння (1) є метод введення допоміжного кута:
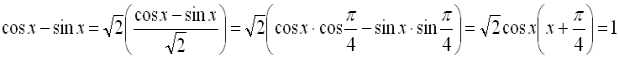
![]()
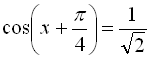
![]()
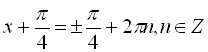
![]()
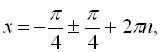
![]() .
.
Друге рівняння сукупності (2) розв’язків не має, оскільки 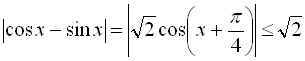 , а число
, а число ![]() .
.
Відповідь: 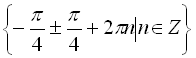 .
.
2.9. Розв’язування тригонометричних рівнянь із застосуванням комбінованих способів
Приклад 22
Розв’язати рівняння ![]() .
.
Розв’язання:
Наведемо дві форми запису розв’язання вихідного рівняння.
І форма запису розв’язання.
ОДЗ: ![]()
![]()
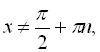
![]() .
.
Знаходимо значення х, що задовольняють рівняння ![]() і
і ![]() ; якщо
; якщо ![]()
![]()
![]()
![]()
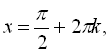
![]() ; якщо
; якщо ![]()
![]()
![]()
![]()
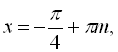
![]() .
.
Оскільки через ОДЗ 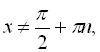
![]() , то серія розв’язків
, то серія розв’язків 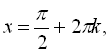
![]() непридатна, вона не входить в ОДЗ, і, відповідно, є лише друга серія розв’язків
непридатна, вона не входить в ОДЗ, і, відповідно, є лише друга серія розв’язків 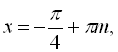
![]() .
.
Відповідь: 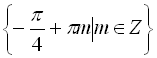 .
.
ІІ форма запису розв’язання.
![]()
![]()
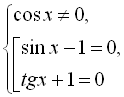
![]()
![]()
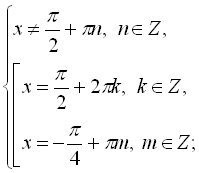
![]()
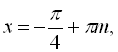
![]() .
.
Відповідь: 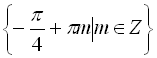 .
.
Приклад 23
Розв’язати рівняння 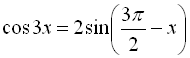 . У відповіді зазначте кількість розв’язків на проміжку
. У відповіді зазначте кількість розв’язків на проміжку ![]()
![]() .
.
Розв’язання:
Скористаємось формулами зведення для правої частини рівняння. 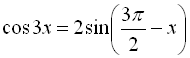
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
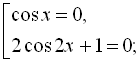
![]()
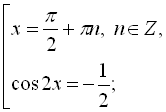
![]()
![]()
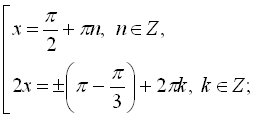
![]()
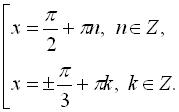
Для ![]()
![]()
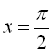 ;
; 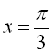 .
.
Отже розв’язків на відрізку ![]()
![]() два.
два.
Відповідь: 2.
Приклад 24
Розв’язати рівняння ![]() .
.
Розв’язання:
![]()
![]()
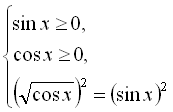
Перші дві тригонометричні нерівності нашої комбінованої системи розв’язуємо з урахуванням властивостей тригонометричних функцій. Тоді маємо: 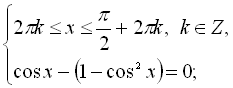
![]()
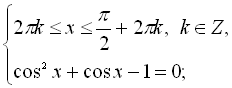
![]()
![]()
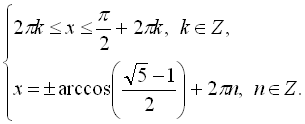
![]()
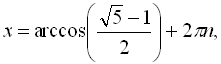
![]() , оскільки друга серія розв’язків зі знаком «–» не задовольняє нерівність
, оскільки друга серія розв’язків зі знаком «–» не задовольняє нерівність 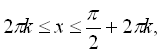
![]() .
.
Відповідь: 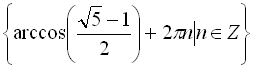 .
.
Приклад 25
Розв’язати рівняння ![]() .
.
Розв’язання:
Оскільки ![]() ,
, ![]() , то
, то
![]() . Знак «=» з урахуванням наведених нерівностей може мати місце тільки у тому випадку, коли
. Знак «=» з урахуванням наведених нерівностей може мати місце тільки у тому випадку, коли
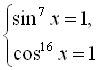
![]()
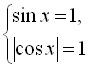
![]()
![]() (оскільки
(оскільки ![]() ).
).
Відповідь:![]() .
.
2.10. Розв’язування тригонометричних рівнянь з параметрами та завдань із застосуванням тригонометричних функцій підвищеної складності
Приклад 26
Визначити кількість цілих значень параметра а, при яких рівняння ![]() має розв’язки.
має розв’язки.
Розв’язання:
![]()
![]()
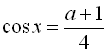 . За властивістю функції
. За властивістю функції ![]() –
– ![]() , тому
, тому 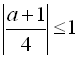
![]()
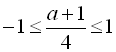
![]()
![]() . Цілими значеннями, які належать отриманому проміжку, є:
. Цілими значеннями, які належать отриманому проміжку, є:
–5; –4; –3; –2; –1; 0; 1; 2; 3. Їх кількість – 9.
Відповідь: 9.
Приклад 27
Розв’яжіть систему рівнянь 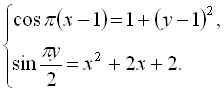
У відповідь запишіть добуток ![]() , якщо
, якщо ![]()
![]() – розв’язок системи рівнянь.
– розв’язок системи рівнянь.
Розв’язання:
Згідно з властивостями тригонометричних функцій, що ![]() та
та 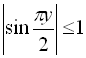 , отримаємо:
, отримаємо: 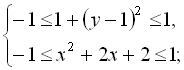 звідки
звідки 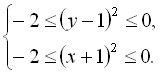 Дана система нерівностей виконується лише при
Дана система нерівностей виконується лише при ![]() ;
; ![]() .
.
Тоді добуток ![]() .
.
Відповідь: ![]() .
.
Приклад 28
Зазначте кількість розв’язків рівняння
![]() на проміжку
на проміжку 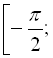
![]() .
.
Розв’язання:
ОДЗ: ![]()
![]()
![]()
![]() .
.
Кожний множник вихідного рівняння прирівняємо до нуля:
![]()
![]()
![]()
![]()
![]() або
або ![]()
![]()
![]()
![]()
![]()
![]()
![]()
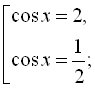
![]()
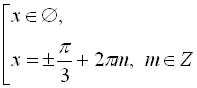
![]()
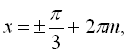
![]() .
.
Отже загальний розв’язок можна записати у вигляді сукупності
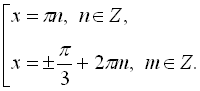 А, враховуючи ОДЗ, коренями на проміжку
А, враховуючи ОДЗ, коренями на проміжку
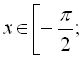
![]() є
є ![]() і
і ![]() .
.
Відповідь: 2 розв’язки.
Приклад 29
Знайдіть усі дійсні значення параметра а, при яких рівняння ![]() має розв’язок.
має розв’язок.
Розв’язання:
Замінимо ![]() через
через ![]() , тоді
, тоді ![]()
![]()
![]()
![]()
![]()
![]() , звідси
, звідси ![]() .
.
Отже, рівняння набуває вигляду ![]()
![]()
![]()
![]() . Розв’яжемо квадратне рівняння відносно змінної
. Розв’яжемо квадратне рівняння відносно змінної ![]() :
:
![]() ;
; 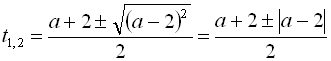
![]()
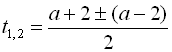
![]()
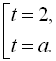
Зробимо оцінку ![]() , для цього розділимо обидві частини рівності
, для цього розділимо обидві частини рівності ![]() на
на ![]() :
: 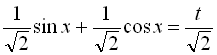 ; за допомогою введення допоміжного кута
; за допомогою введення допоміжного кута 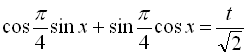
![]()
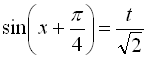 (І). Оскільки
(І). Оскільки 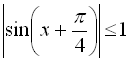 , то й
, то й 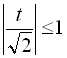 , тобто
, тобто 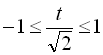
![]()
![]() , або
, або ![]() .
.
Отже, ![]() не задовольняє наші умови, тому
не задовольняє наші умови, тому ![]() , а оскільки
, а оскільки ![]() , то і
, то і ![]() , і з рівності (І)
, і з рівності (І) ![]()
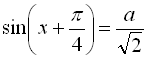
![]()
![]()
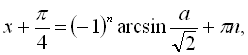
![]()
![]()
![]()
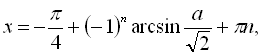
![]() .
.
Відповідь: для 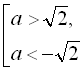 розв’язків немає;
розв’язків немає;
для ![]()
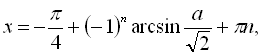
![]() .
.
Приклад 30
Зазначте усі дійсні значення параметра а, при яких рівняння 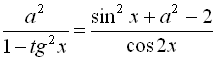 має розв’язки.
має розв’язки.
Знайдіть ці розв’язки.
Розв’язання:
Знайдемо ОДЗ:
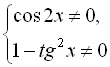
![]()
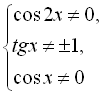
![]()
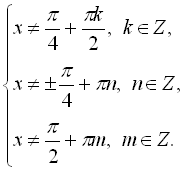
Оскільки перше й друге значення однакові, то в ОДЗ входять будь-які х, окрім 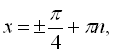
![]() (І) і
(І) і 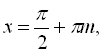
![]() (ІІ).
(ІІ).
Перетворимо вихідне рівняння за допомогою тригонометричних формул: 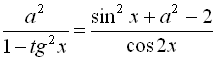
![]()
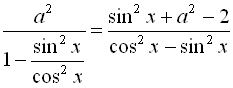
![]()
![]()
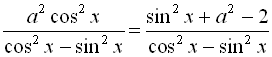 .
.
Врахувавши ОДЗ: ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Оскільки
. Оскільки ![]() для будь-яких а, то
для будь-яких а, то 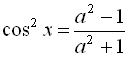 ; згідно з формулою пониження степеня
; згідно з формулою пониження степеня
маємо 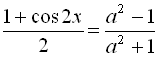
![]()
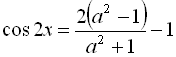
![]()
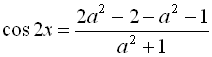
![]()
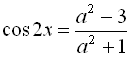 . Оскільки
. Оскільки ![]() , то й
, то й 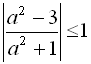 або
або 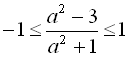
![]()
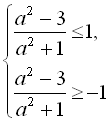
![]()
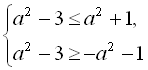
![]()
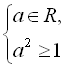
![]()
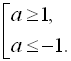 Крім того, згідно з (І) і (ІІ), отримане рівняння
Крім того, згідно з (І) і (ІІ), отримане рівняння 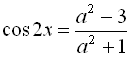 має розв’язок, якщо
має розв’язок, якщо 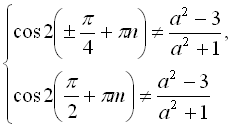
![]()
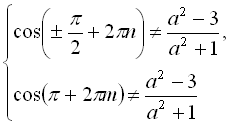
![]()
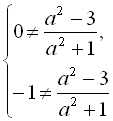
![]()
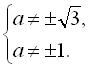
Отже, 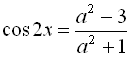 для
для ![]() ,
, ![]() ,
, 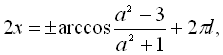
![]()
![]()
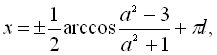
![]() .
.
Відповідь: для ![]() і
і ![]() розв’язків немає.
розв’язків немає.
для ![]() і
і ![]()
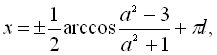
![]() .
.
2.11. Тренувальні вправи
Завдання 1. Розв’язати найпростіші тригонометричні рівняння.
1. ![]() ;
;
2. 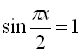 ;
;
3. ![]() ;
;
4. 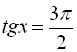 ;
;
5. 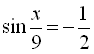 ;
;
6. ![]() ;
;
7. 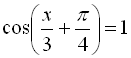 ;
;
8. 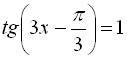 ;
;
9. 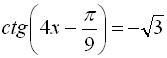 ;
;
10. 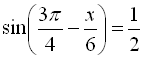 ;
;
11. 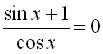 ;
;
12. 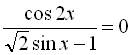 ;
;
13. 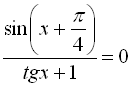 ;
;
14. ![]() ;
;
15. 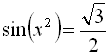 .
.
16. Визначити найменший розв’язок рівняння 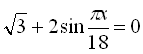 , який належить проміжку (20; 60).
, який належить проміжку (20; 60).
Завдання 2. Розв’язати рівняння способом приведення до однієї з функцій.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. 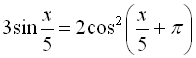 ;
;
6. 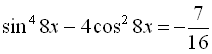 .
.
Завдання 3. Розв’язати однорідні рівняння і ті, що до них зводяться.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() .
.
Завдання 4. Розв’язати рівняння за допомогою універсальної підстановки.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
Завдання 5. Розв’язати рівняння методом введення допоміжного аргументу.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. 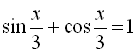 ;
;
5. 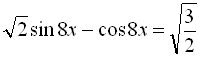 ;
;
6. 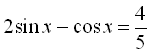 .
.
Завдання 6. Розв’язати рівняння, застосовуючи формули пониження степеня.
1. 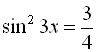 ;
;
2. 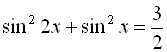 ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. 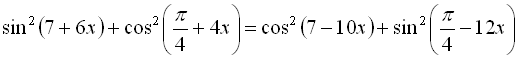 .
.
7. Вказати кількість розв’язків рівняння 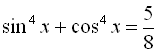 на проміжку
на проміжку ![]()
![]() .
.
Завдання 7. Розв’язати рівняння, використовуючи заміну змінної.
1. ![]() ;
;
2. 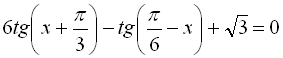 ;
;
3. ![]() ;
;
4. ![]() ;
;
5. 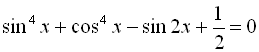 ;
;
6. 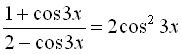 .
.
Завдання 8. Розв’язати тригонометричні рівняння, використовуючи різні методи.
1. 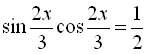 ;
;
2. 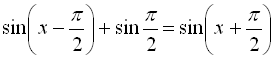 ;
;
3. 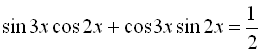 ;
;
4. 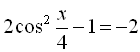 ;
;
5. ![]() ;
;
6. ![]() ;
;
7. ![]() ;
;
8. ![]() ;
;
9. ![]() ;
;
10. ![]() ;
;
11. ![]() ;
;
12. ![]() ;
;
13. ![]() ;
;
14. ![]() ;
;
15. ![]() ;
;
16. 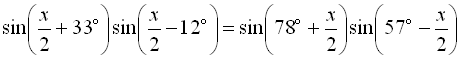 ;
;
17. ![]() ;
;
18. ![]() ;
;
19. Зазначте кількість розв’язків рівняння
![]() на проміжку
на проміжку ![]()
![]() ;
;
20. Зазначте кількість розв’язків рівняння ![]() на проміжку
на проміжку ![]()
![]() ;
;
21. 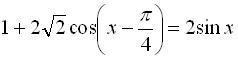 ;
;
22. 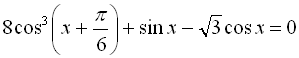 ;
;
23. ![]() ;
;
24. ![]() ;
;
25. ![]() ;
;
26. ![]() ;
;
27. ![]() ;
;
28. ![]() ;
;
29. ![]() ;
;
30. ![]() .
.
Список використаної літератури
- Алєксєєв В. М. Математика. Довідковий повторювальний курс : навч. посібник / Алєксєєв В. М., Ушаков Р. П. ; за ред. М. Й. Ядренка. – К. : Вища шк., 1992. – 295 с.
- Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики (навчальний посібник для студентів ВНЗ І-ІІ р.а.) – К.: Вища школа, 2001.
- Бондаренко М. Ф. Математика для вступників до вузів : навч. посібник / М. Ф. Бондаренко, В. А. Дікарєв, О. Ф. Мельников та інші. – Харків : «Компанія СМІТ», 2002. – 1120 с.
- Гальперіна А. Р. Математика. Типові тестові завдання : збірник /
А. Р. Гальперіна, О. Я. Михєєва. – Х. : Веста, 2009. – 128 с. + Додат.
(16 с.). – (Серія журналу «Вісник ТІМО»).
- Егоров В. К. Сборник задач по математике для поступающих в вузы /В. К. Егоров, В. В. Зайцев, Б. А. Кордомский ; под ред. М. И. Сканави. – М. : Высшая школа, 1992. – 528 с.
- Литвиненко В. И. Практикум по элементарной математике / В. И. Литвиненко. – М. : Просвещение, 1991. – 352 с.
- Письменный Д. Т. Готовимся к экзамену по математике : домашний репетитор / Письменный Д. Т. – М. : Рольф, 1999. – 288 с.
- Роєва Т.Г., Адруг Л.М. Математика. Інтегровний курс. Тематичне оцінювання. 10, 11 кл. – К.: Країна мрій, 2007.
- Слєпкань З.І., Грохольська А.В. Збірник задач з алгебри і початків аналізу, 10-11 кл. – К.: Підручники і посібники, 2003.
- Титаренко О. М. Форсований курс шкільної математики : навчальний посібник / Титаренко О. М. – Харків : ТОРСІНГ ПЛЮС, 2005. – 368 с.
- Титаренко О. 5770 задач з математики з відповідями. / Титаренко О. М. – Харків : ТОРСІНГ ПЛЮС, 2005. – 336 с.
1


про публікацію авторської розробки
Додати розробку