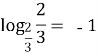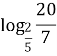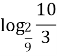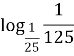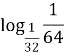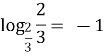Методична розробка відкритого заняття з теми "Тотожні перетворення логарифмічних виразів"
МЕТОДИЧНА РОЗРОБКА
ВІДКРИТОГО ЗАНЯТТЯ
Логарифми. Тотожні перетворення логарифмічних виразів
з навчальної дисципліни «Математика»
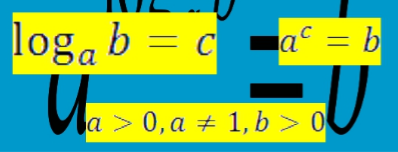
ЗМІСТ
|
Структура заняття |
|
Хід заняття |
|
Додаток А. Самостійна робота «Знайди помилку» |
|
Додаток Б. Математичний диктант |
|
Додаток В. Виступ-доповідь студентки з теми «Історія виникнення логарифмів» |
|
Додаток Г. Самостійна робота студентів на порівняти логарифмічних виразів з нулем |
|
Додаток Д. Виступ-доповідь студентки з теми «Практичне використання логарифмів» |
|
Додаток Е. Самостійна робота |
|
Додаток Ж. Картка-план заняття та оцінювання студента |
|
Додаток З. Буклет з опорним конспектом |
|
Додаток І. Таблиця для зарахування балів студенту |
СТРУКТУРА ЗАНЯТТЯ
1. Організаційна частина
2. Ознайомлення студентів із умовами проведення заняття
3. Ознайомлення студентів з темою, метою заняття. Мотивація вивчення теми
4. Актуалізація опорних знань
4.1Виконання усних вправ:
4.2 Означення логарифму
4.3 Розв’язування вправ за двома варіантами
4.4 Математичний диктант
4.5.Виступ-доповідь студентки з теми «Історія виникнення логарифмів»
5. Практичне заняття.
5.1 Розв'язання задач на закріплення означення логарифма
5.2 Розв'язання задач на застосування логарифмічних тотожностей та властивостей
5.3 Виступ-доповідь студентки з теми «Практичне використання логарифмів»
6. Розв'язання задач.
6.1 Колективне розв’язання вправи на закріплення
6.2 Самостійна робота по варіантам
7. Підсумок заняття
7.1 Повторення основних понять
7.2 Виставлення балів за заняття.
8. Домашнє завдання
Хід заняття
1.Організаційний момент
1.1Привітання студентів
1.2Підготовка аудиторії до заняття, перевірка наявності студентів
2. Ознайомлення студентів із умовами проведення заняття
Викладач. Сьогодні на занятті ми спробуємо об’єктивно оцінити свої знання, вміння та навички з теми «Логарифми». Для цього спочатку подивимося на парту: в нас є аркуш з планом-заняття та прикладами, які ми будемо розв’язувати колективно та індивідуально. Жовтим кольором помічені завдання, які треба розв’язати самостійно згідно свого варіанта. А оцінювати та перевіряти їх буде ваш сусід по парті. Звісно, як і ви його. У кінці кожний получить оцінку. Побачимо рівень підготовки кожного.
3. Мотивація навчання
У житті існують такі процеси, які не піддаються опису за допомогою простих алгебраїчних функцій (які ми вивчали у курсі середньої школи), але з достатньою точністю характеризуються більш складними функціями. Серед цих функцій важливе значення має логарифмічна. Вона служить математичною формою вираження процесів природного зростання або спадання величин. Вивчення властивостей логарифмічної функції має значимість не тільки в математичній освіті, а й у формуванні нашого мислення, щодо розуміння зв'язку навчання математики з життям. Тому треба чітко знати означення, формули, правила обчислення та вміти їх застосовувати на практиці.
4. Актуалізація опорних знань
4.1Виконання усних вправ:
Для початку, щоб ліпше налаштуватися, усі разом, піднімаючи руку, знайдемо значення кореня для записаних рівнянь:
1) 7х = 49 2) 196х = 1 3) 5х = 
4) 3х = 
5) 2х = - 8 6) 10х = 0,001 7) 2х = 3
х = 2 х = 0 х= -1 х= 
х= 
х= -3 х= 
( прийом «мозковий штурм» )
4.2 Означення логарифму
Логарифм (
- число х (показник степеня, степінь), яке показує, до якого степеня слід піднести число a (основу), щоб одержати число b.
При чому a – основа, a
, b
№1. Знайти логарифми чисел за основою 3:
|
|
|
|
0 |
1 |
3 |
9 |
27 |
81 |
|
|
-2 |
-1 |
|
0 |
1 |
2 |
3 |
4 |
4.3 Розв’язування вправ за двома варіантами
Знайти помилки у відповідях: (Додаток А)
|
Варіант 1 |
Варіант 2 |
||||
|
1 |
|
|
1 |
|
|
|
2 |
|
|
2 |
|
+ |
|
3 |
|
+ |
3 |
|
|
|
4 |
|
|
4 |
|
+ |
|
5 |
lg 0,001= 4 |
+ |
5 |
|
+ |
|
6 |
|
+ |
6 |
lg1000 = 3 |
|
(Самоперевірка – викладач промовляє уголос відповіді з коментарем студентів.
За кожну правильну відповідь – 1 бал, всього 3 бали)
4.4 Математичний диктант (Додаток Б)
- самостійна робота студентів
|
№ |
Завдання |
Відповідь |
|
1 |
|
|
|
2 |
lg1 |
|
|
3 |
|
|
|
4 |
|
|
|
5 |
lg |
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
(Взаємоперевірка - студенти обмінюються зошитами з відповідями з сусідом по парті. За кожну правильну відповідь – 1 бал, всього 10 балів)
4.5.Виступ-доповідь студентки з теми «Історія виникнення логарифмів»
(додається презентація) (Додаток В)
5. Практичне заняття.
5.1 Розв'язання задач на закріплення означення логарифма
- усі студенти разом (не на оцінку, це підготовчий етап)
№2. Заповнити таблицю значеннями згідно свого варіанту:
|
Варіант 1 |
Варіант 2 |
||||||||||||||
|
|
|
|
1 |
2 |
4 |
8 |
16 |
|
|
|
1 |
2 |
4 |
8 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповіді:
|
Варіант 1 |
Варіант 2 |
||||||||||||||
|
|
|
|
1 |
2 |
4 |
8 |
16 |
|
|
|
1 |
2 |
4 |
8 |
16 |
|
|
-2
|
-1 |
0 |
1 |
2 |
3 |
4 |
|
2 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
Висновки: Коли a
значення зростають, а коли 
a
значення спадають.
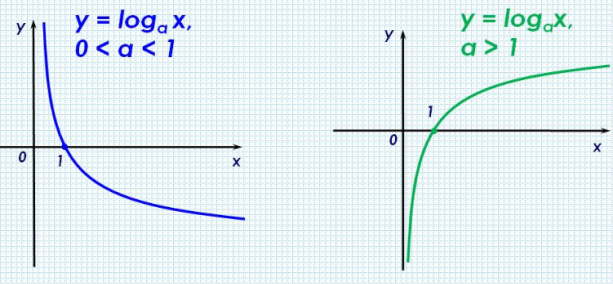
Властивість логарифмічної функції у = 
:
– якщо a
- функція зростаюча,
- якщо a - функція спадаюча.
№3. Порівняти вирази:
1) 
та 
2) 
та 
3) 
та 
4) 
та 
5) 
та 
- самостійна робота студентів (Додаток Г)
№4. Порівняти з нулем вирази: Варіант 1
|
№ |
вираз |
знак |
|
№ |
вираз |
знак |
№ |
|
1 |
|
|
0 |
5 |
|
|
0 |
|
2 |
|
|
0 |
6 |
|
|
0 |
|
3 |
|
|
0 |
7 |
|
|
0 |
|
4 |
|
|
0 |
8 |
|
|
0 |
Варіант 2
|
№ |
вираз |
знак |
|
№ |
вираз |
знак |
№ |
|
1 |
|
|
0 |
5 |
|
|
0 |
|
2 |
|
|
0 |
6 |
|
|
0 |
|
3 |
|
|
0 |
7 |
|
|
0 |
|
4 |
|
|
0 |
8 |
|
|
0 |
(Взаємоперевірка - студенти обмінюються зошитами з відповідями з сусідом по парті. За кожну правильну відповідь – 1 бал, всього 8 балів)
- колективна робота студентів, 1 студент біля дошки:
№5. Обчислити логарифми:
5.2 Розв'язання задач на застосування логарифмічних тотожностей та властивостей
5.2.1 Викладач. Згадаємо ще дві важливі формули. Знаючи, логарифмічна функція обернена до показникової, робимо висновок, що з формули
слідує формула 
слідує формула 
№6. Знайти значення виразів:
1) 
2) 
3) 
5.2.2 Викладач. З означення логарифму числа слідує основна логарифмічна
тотожність: 
Приклади:
№7.(усно) 1) 
2) (
3) 
5.2.3 Викладач. Час нагадати формулу про ступені: 
Приклади:
№8. 1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
5.2.4 Викладач. Як розв’язати завдання, коли зустрічаються декілька логарифмів і усі з різними основами?
Згадуємо формулу переходу до нової основи: 
№9. Обчислити:
1)
5.3 Виступ-доповідь студентки з теми «Практичне використання логарифмів» (Додаток Д)
6. Розв'язання задач.
Викладач. А тепер відпрацюємо отримані знання на практиці
- колективне розв’язання вправи на закріплення: на дошці
№10. Знайти значення виразів:
1) 
2) lg(
)
3) 
- Самостійна робота (Додаток Е)
|
№ |
Варіант 1 |
№ |
Варіант 2 |
|
1 |
2 |
1 |
|
|
2 |
|
2 |
|
|
3 |
|
3 |
|
|
4 |
|
4 |
|
|
5 |
|
5 |
|
(Взаємоперевірка - студенти обмінюються зошитами з відповідями з сусідом по парті. За кожну правильну відповідь – 1 бал, всього 5 балів)
7. Підсумок заняття. .
7.1 Повторення основних понять
1. Логарифми.
2. Властивості та тотожності логарифмів.
7.2 Виставлення балів за заняття.
- провести нарахування балів за кожний етап заняття (Додаток І)
8. Домашнє завдання.
- Розв’язати вправи:
№1. Обчислити:
1) 
2) 
3) 
4) 
5) 
Додаток А
Знайти помилки у відповідях:
|
Варіант 1 |
Варіант 2 |
||||
|
1 |
|
|
1 |
|
|
|
2 |
|
|
2 |
|
|
|
3 |
|
|
3 |
|
|
|
4 |
|
|
4 |
|
|
|
5 |
lg 0,001= 4 |
|
5 |
|
|
|
6 |
|
|
6 |
lg1000 = 3 |
|
Відповіді:
|
Варіант 1 |
Варіант 2 |
||||
|
1 |
|
|
1 |
|
|
|
2 |
|
|
2 |
|
+ |
|
3 |
|
+ |
3 |
|
|
|
4 |
|
|
4 |
|
+ |
|
5 |
lg 0,001= 4 |
+ |
5 |
|
+ |
|
6 |
|
+ |
6 |
lg1000 = 3 |
|
Додаток Б
Математичний диктант
|
№ |
Завдання |
Відповідь |
|
1 |
|
|
|
2 |
lg1 |
|
|
3 |
|
|
|
4 |
|
|
|
5 |
lg |
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
Відповіді:
|
№ |
Завдання |
Відповідь |
|
1 |
|
9 |
|
2 |
lg1 |
0 |
|
3 |
|
4 |
|
4 |
|
-1 |
|
5 |
lg |
-2 |
|
6 |
|
-4 |
|
7 |
|
-2 |
|
8 |
|
6 |
|
9 |
|
|
|
10 |
|
0 |
Додаток В
Виступ-доповідь студентки з теми «Історія виникнення логарифмів»
Історія логарифмів, як алгебраїчного поняття, простежується з античних часів. Ідейним джерелом і стимулом застосування логарифмів послужив той факт, що при перемножуванні ступенів з однаковою основою їх показники складаються: 
.
У 1614 році шотландський математик-аматор Джон Непер опублікував твір під назвою «Опис дивовижної таблиці логарифмів». У ньому був короткий опис логарифмів і їх властивостей, а також 8-значні таблиці логарифмів синусів, косинусів і тангенсів, з кроком 1'. Термін логарифм, запропонований Непером, утвердився в науці. Теорію логарифмів Непер виклав в іншій своїй книзі «Побудова дивовижної таблиці логарифмів», виданої посмертно, в 1619 році його сином Робертом.
З властивостей логарифма випливає, що замість трудомісткого множення багатозначних чисел досить знайти (за таблицями) і скласти їх логарифми, а потім з тих же таблиць виконати потенцювання, тобто знайти значення результату за його логарифмом. Виконання ділення відрізняється тільки тим, що логарифми віднімаються.
Судячи з документів, технікою логарифмування Непер володів вже до 1594 року. Безпосередньою метою її розробки було полегшити складні астрологічні розрахунки, саме тому в таблиці було включено тільки логарифми тригонометричних функцій.
Як згодом виявилось, через помилки в алгоритмі усі значення таблиці Непера містили невірні цифри після шостого знака. Однак це не завадило новій методиці обчислень отримати найширшу популярність, і складанням логарифмічних таблиць зайнялись багато європейських математиків. Йоганн Кеплер у 1624 році опублікував свій варіант логарифмічних таблиць. Використання логарифмів дозволило Кеплеру відносно швидко завершити багаторічну працю по складанню Рудольфінських таблиць, які закріпили успіх геліоцентричної астрономії.
Через кілька років після книги Непера з'явилися логарифмічні таблиці, що використовують більш близьке до сучасного розуміння логарифма. Лондонський професор Генрі Брігс видав 14-значні таблиці десяткових логарифмів (1617), причому не для тригонометричних функцій, а для довільних цілих чисел до 1000. В 1619 лондонський вчитель математики Джон Спайделл перевидав логарифмічні таблиці Непера, виправлені і доповнені так, що вони фактично стали таблицями натуральних логарифмів.
У 1617 году Оксфордський професор математики Генрі Брігс опублікував таблиці, які вже включали десяткові логарифми самих чисел, від 1 до 1000, з 8 (пізніше — з 14) знаками. Але і в таблицях Брігса виявилися помилки. Перше безпомилкове видання на основі таблиць Георга Веги (1783) з'явилося тільки в 1857 році в Берліні.
У 1620-і роки Едмунд Уінгейт і Вільям Отред винайшли першу логарифмічну лінійку, до появи кишенькових калькуляторів вона служила незамінним розрахунковим знаряддям інженера.
За допомогою цього компактного інструменту можна швидко робити всі алгебраїчні операції, в тому числі за участю тригонометричних функцій. Точність розрахунків — близько 3 значущих цифр.
Незабаром з'ясувалося, що місце логарифмів в математиці не обмежується розрахунковими зручностями.
На думку багатьох істориків, поява логарифмів значно вплинула на багато математичних концепцій, в тому числі на:
1.Формування і визнання загального поняття ірраціональних і трансцендентних чисел.
2.Поява показової функції і загального поняття числової функції, числа Ейлера, розвиток теорії різницевих рівнянь
3.Початок роботи з нескінченними рядам.
4.Загальні методи рішення диференціальних рівнянь різних типів.
5.Істотний розвиток теорії чисельних методів, необхідних для обчислення точних логарифмічних таблиць.
Додаток Г
Самостійна робота студентів на порівняти логарифмічних виразів з нулем
Варіант 1
|
№ |
вираз |
знак |
|
№ |
вираз |
знак |
№ |
|
1 |
|
|
0 |
5 |
|
|
0 |
|
2 |
|
|
0 |
6 |
|
|
0 |
|
3 |
|
|
0 |
7 |
|
|
0 |
|
4 |
|
|
0 |
8 |
|
|
0 |
Відповіді:
|
№ |
вираз |
знак |
|
№ |
вираз |
знак |
№ |
|
1 |
|
|
0 |
5 |
|
|
0 |
|
2 |
|
|
0 |
6 |
|
|
0 |
|
3 |
|
|
0 |
7 |
|
|
0 |
|
4 |
|
|
0 |
8 |
|
|
0 |
Самостійна робота студентів на порівняти логарифмічних виразів з нулем
Варіант 2
|
№ |
вираз |
знак |
|
№ |
вираз |
знак |
№ |
|
1 |
|
|
0 |
5 |
|
|
0 |
|
2 |
|
|
0 |
6 |
|
|
0 |
|
3 |
|
|
0 |
7 |
|
|
0 |
|
4 |
|
|
0 |
8 |
|
|
0 |
Відповіді:
|
№ |
вираз |
знак |
|
№ |
вираз |
знак |
№ |
|
1 |
|
|
0 |
5 |
|
|
0 |
|
2 |
|
|
0 |
6 |
|
|
0 |
|
3 |
|
|
0 |
7 |
|
|
0 |
|
4 |
|
|
0 |
8 |
|
|
0 |
Додаток Д
Виступ-доповідь студентки з теми «Практичне використання логарифмів»
Споконвіку метою математичної науки було допомогти людям дізнатися більше про навколишній світ, пізнати його закономірності та таємниці. Ряд явищ природи допомагає описати саме логарифмічна залежність.
Одним з найбільш наочних прикладів є логарифмічна спіраль.
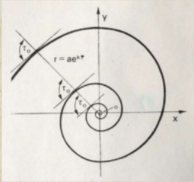Спіралі - плоскі криві лінії, багаторазово обходять одну з точок на площині, яка називається полюсом спіралі.
Логарифмічна спіраль — особливий вид спіралі. Логарифмічна спіраль є траєкторією точки, яка рухається вздовж прямої, що рівномірно обертається, віддаляючись від полюса зі швидкістю, пропорційною пройденій відстані.
Спіраль називається логарифмічною тому, що логарифм відстані ( 
) ) пропорційний куту поворота.
У полярних координатах рівняння кривої може бути записано як
або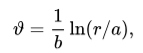 
що пояснює назву «логарифмічна».
Логарифмічна спіраль часто зустрічається в природі.
Можна сказати, що спіраль є математичним символом співвідношення форми i зростання.
Наприклад, раковини морських тварин можуть рости лише в одному напрямку. Щоб не дуже витягуватися в довжину, їм доводиться скручуватися, причому кожен наступний виток подібний до попереднього. А таке зростання може відбуватися лише за логарифмічною спіралі або її аналогій. Тому раковини багатьох молюсків, равликів, закручені за логарифмічною спіралі.
Хижі птахи кружляють над видобутком за логарифмічною спіралі. Справа в тому, що вони краще бачать, якщо дивляться не прямо на видобуток, а трохи вбік.
Один з найбільш поширених павуків Епейра, сплітаючи павутину, закручує нитки навколо центра за логарифмічною спіраллю.
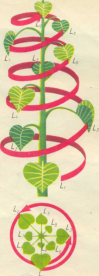
Спірально закручуються вусики рослин, по спіралі відбувається зростання тканин в стовбурах дерев.
Роги таких рогатих ссавців, як архари (гірські козли), закручені за логарифмічною спіралі.
У соняшнику насіння розташовані по дугам, близьким до логарифмічною спіралі.
За логарифмичними спіралями закручені і багато галактик, зокрема Галактика, якій належить Сонячна система.
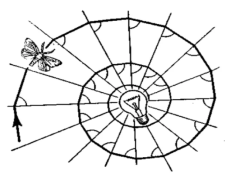
Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельних промінням місяця, інстинктивно зберігають постійний кут між напрямком польоту і променем світла.
Якщо вони орієнтуються на точкове джерело світла (полум'я свічки) то інстинкт їх підводить, и метелики потрапляють в полум'я по логарифмічної спіралі, що скручується.
Логарифми широко використовуються в різних областях наук:
Фізика - інтенсивність звуку (децибели) оцінюється рівнем інтенсивності за шкалою децибел:
число децибел N = 10lg (I / I0), де I - інтенсивність даного звуку
Подібним чином оцінюється і гучність шуму. Гучність шуму виражена у белах дорівнює десятковому логарифму його фізичної сили.
Астрономія
Астрономи розподіляють зірки за ступенями видимої яскравості на світила першої, другої, третьої величини і так далі. Величина зірки являє собою логарифм її фізичної яркості. Оценівая видиму яскравість зірок астроном оперує таблицями логарифмів, складеними по основі 2.
Якщо відома видима зоряна величина і відстань до об'єкта, можна обчислити абсолютну зоряну величину за формулою:
Хімія Водневий показник, "pH", - це міра активності іонів водню в розчині, кількісно виражає його кислотність.
Водневій показник - це від'ємній десятковій логарифм концентрації водневих йонів, вираженої в молях на літр:
рН = - lg С (Н +)
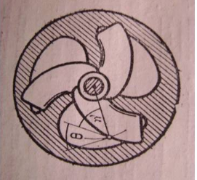
У техніці: застосовують обертові ножі. Для сталості тиску потрібно, щоб кут різання зберігав постійне значення, це відбувається в тому випадку, якщо леза ножів окреслені по дузі логарифмічною спіралі.
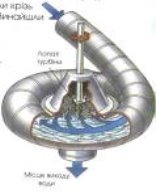У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними, і напір води використовується з максимальною продуктивністю.
У будівництві: Під час будівництва ставків необхідно враховувати кількість води, що буде прибувати у ставок у період повені. Розрахунки проводяться за допомогою логарифмів.
У сейсмології:
При обчисленні магнітуди. Магнітуда землетрусу - величина, що характеризує енергію, що виділилася при землетрусі у вигляді сейсмических волн.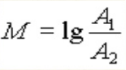 
У музиці:
В основі пристрою музичної гами лежать певні закономірності. Для побудови гами набагато зручніше користуватися, виявляється, логарифмами відповідних частот: log 2w0, log 2w1 ... log 2wm
Номери клавіш рояля є логарифми чисел коливання відповідніх звуків. Ми даже можемо сказати, що номер октави є характеристикою, а номер звуку в даній октаві - мантіс (дробова частина логарифма числа) цього логарифма.
Логарифмічна функція моделює такі процеси:
- закон зміни роботи газу;
- закон зміни сили відчуття від сили збудження (психофізичний закон Вебера);
- закон зміни тиску від зміни висоти;
- тривалість хімічної реакції;
- залежність збільшення величини банківського вкладу від пройденого часу.
Додаток Е
Самостійна робота
|
№ |
Варіант 1 |
№ |
Варіант 2 |
|
1 |
2 |
1 |
|
|
2 |
|
2 |
|
|
3 |
|
3 |
|
|
4 |
|
4 |
|
|
5 |
|
5 |
|
Відповіді:
|
№ |
Варіант 1 |
№ |
Варіант 2 |
|
1 |
14 |
1 |
-5 |
|
2 |
1,5 |
2 |
1,2 |
|
3 |
2 |
3 |
3 |
|
4 |
|
4 |
|
|
5 |
20,5 |
5 |
100,1 |
Додаток Ж
Картка-план заняття та оцінювання студента (на кожній парті)
Прізвище____________________________ Варіант 1
Тема: Логарифми. Тотожні перетворення логарифмічних виразів
№1. Знайти логарифми чисел за основою 3:
|
|
|
|
0 |
1 |
3 |
9 |
27 |
81 |
|
|
|
|
|
|
|
|
|
|
- Знайти помилки у відповідях
|
Варіант 1 |
|||
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
lg 0,001= 4 |
|
|
|
6 |
|
|
|
- Математичний диктант
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Заповнити таблицю значеннями згідно свого варіанту:
|
Варіант 1 |
|||||||
|
|
|
|
1 |
2 |
4 |
8 |
16 |
|
|
|
|
|
|
|
|
|
№3. Порівняти вирази: УСНО
1) __ 
4) __ 5) __
- самостійна робота студентів
№4. Порівняти з нулем вирази: Варіант 1
|
№ |
вираз |
знак |
|
|
№ |
вираз |
знак |
№ |
|
|
1 |
|
|
0 |
|
5 |
|
|
0 |
|
|
2 |
|
|
0 |
|
6 |
|
|
0 |
|
|
3 |
|
|
0 |
|
7 |
|
|
0 |
|
|
4 |
|
|
0 |
|
8 |
|
|
0 |
|
- колективна робота студентів, 1 студент біля дошки:
№5. Обчислити логарифми:
-
= ______________________________________________
-
= ________________________________________________
-
= ____________________________________________
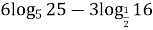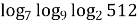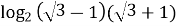№6. Знайти значення виразів:
1) = _____________________________________________________
2) = ___________________________________________________
3) = ______________________________________________________
№7. УСНО 1) 2) ( 
3)
№8. 1) = ____ 2) = ____ 3) = ____ 4) = ____
5) = _________________________ 6) 
= ________________________
7) 
8) 
9) = ________
? №9. Як розв’язати завдання, коли зустрічаються декілька логарифмів і усі з різними основами?
= ______________________________________________
№10. Знайти значення виразів:
1) = _________________________________________
2) lg() = _______________________________________________
3) = _________________________________________________________
- самостійна робота студентів
|
№ |
Варіант 1 |
Відповідь |
Перевірка |
|
|
1 |
2 |
|
|
1 |
|
2 |
|
|
|
1 |
|
3 |
|
|
|
1 |
|
4 |
|
|
|
2 |
|
5 |
|
|
|
2 |
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Всього балів: ___________ Оцінка: ________________
Картка-план заняття та оцінювання студента (на кожній парті)
Прізвище____________________________ Варіант 2
Тема: Логарифми. Тотожні перетворення логарифмічних виразів
№1. Знайти логарифми чисел за основою 3:
|
|
|
|
0 |
1 |
3 |
9 |
27 |
81 |
|
|
|
|
|
|
|
|
|
|
- Знайти помилки у відповідях
|
Варіант 2 |
|||
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
lg1000 = 3 |
|
|
- Математичний диктант
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Заповнити таблицю значеннями згідно свого варіанту:
|
Варіант 2 |
|||||||
|
|
|
|
1 |
2 |
4 |
8 |
16 |
|
|
|
|
|
|
|
|
|
№3. Порівняти вирази: УСНО
1) __ 4) __ 5) __
- самостійна робота студентів
№4. Порівняти з нулем вирази: Варіант 2
|
№ |
вираз |
знак |
|
|
№ |
вираз |
знак |
|
|
|
1 |
|
|
0 |
|
5 |
|
|
0 |
|
|
2 |
|
|
0 |
|
6 |
|
|
0 |
|
|
3 |
|
|
0 |
|
7 |
|
|
0 |
|
|
4 |
|
|
0 |
|
8 |
|
|
0 |
|
- колективна робота студентів, 1 студент біля дошки:
№5. Обчислити логарифми:
-
= ______________________________________________
-
= ________________________________________________
-
= ____________________________________________
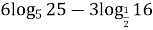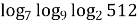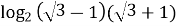№6. Знайти значення виразів:
1) = _____________________________________________________
2) = ___________________________________________________
3) = ______________________________________________________
№7. УСНО 1) 2) ( 3)
№8. 1) = ____ 2) = ____ 3) = ____ 4) = ____
5) = _________________________ 6) = ________________________
7) 8) 9) = ________
? №9. Як розв’язати завдання, коли зустрічаються декілька логарифмів і усі з різними основами?
= ______________________________________________
№10. Знайти значення виразів:
1) = _________________________________________
2) lg() = _______________________________________________
3) = _________________________________________________________
- самостійна робота студентів
|
№ |
Варіант 2 |
Відповідь |
Перевірка |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
1 |
|
3 |
|
|
|
1 |
|
4 |
|
|
|
2 |
|
5 |
|
|
|
2 |
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Всього балів: ___________ Оцінка: ________________
Додаток З
Додаток І
Таблиця для зарахування балів студенту
|
Бали |
15-16 |
17-18 |
19-20 |
21-22
|
23-24
|
25-26
|
27-28
|
29-30
|
31-32
|
|
Оцінка
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Оцінювання:
- усі завдання – по 1 балу
окрім останньої самостійної роботи, в ній 4) та 5) по 2 бали
- 2 бали за №8 або №10 (розв’язаний раніше ніж на дошці)
- у дошки – 2 бали
-
як обчислити 5 завдання домашньої роботи?
про публікацію авторської розробки
Додати розробку