Визначений інтеграл та його властивості.
Тема уроку: Приклади задач, що приводять до поняття інтеграла. Означення інтеграла
Мета уроку: Познайомити учнів з задачами, які приводять до поняття інтеграла: задача про площу криволінійної трапеції. Формування поняття інтеграла.
І. Перевірка домашнього завдання.
Перевірити правильність виконання домашніх завдань за записами, зробленими до початку уроку:
№ 3 (розділ IX).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
№ 3 (розділ X)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
II. Самостійна робота.
Варіант 1
1. Для функції f(x) = 3х2 знайдіть первісну, графік якої проходить через точку А(0; 1). (4 бали)
2. Знайдіть загальний вигляд первісних для. функцій:
a) f(x) = cos 2x + sin Зх; б) f(x) = ![]() . (4 бали)
. (4 бали)
3. Знайдіть невизначені інтеграли: a) ![]() ; б)
; б) ![]() . (4 бали) Варіант 2
. (4 бали) Варіант 2
1. Для функції f(x) = 4х3 знайдіть первісну, графік якої проходить через точку А(0; 1). (4 бали)
2. Знайдіть загальний вигляд первісних для функцій:
a) f(x) = ![]() ; б) f(x) =
; б) f(x) = ![]() . (4 бали)
. (4 бали)
3. Знайдіть невизначені інтеграли: a) ![]() ; б)
; б) ![]() . (4 бали)
. (4 бали)
Відповідь: В-1. 1. F(x) = x3 + 1. 2. a) F(x) = ![]() sin2x –
sin2x – ![]() cos3x + C;
cos3x + C;
б) ![]() . 3. а)
. 3. а) ![]() ; б) tg(3x - 1) + С.
; б) tg(3x - 1) + С.
В-2. 1. F(x) = х4 + 1, 2. a) F(x) = ![]() tg 2х + ctg х + С;
tg 2х + ctg х + С;
б) ![]() . 3. a)
. 3. a) ![]() ; б) sin (3х + 2) + С.
; б) sin (3х + 2) + С.
III. Сприймання і усвідомлення матеріалу про криволінійну трапецію та її площу.
 У попередніх класах ви навчилися обчислювати площі прямокутника, трикутника, паралелограма, трапеції, довільного многокутника, а також площі круга та його частин.
У попередніх класах ви навчилися обчислювати площі прямокутника, трикутника, паралелограма, трапеції, довільного многокутника, а також площі круга та його частин.
У математиці розроблено методи, що дозволяють обчислювати площі фігур, межа яких складається з кривих ліній.
Тепер, використовуючи знання про первісну функції, ми навчимося знаходити площі фігур, які називаються криволінійними трапеціями.
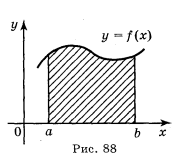
Криволінійною трапецією називається фігура, обмежена графіком неперервної функції у = f(x), яка не змінює знак на відрізку [а; b], прямими x = а, х = b і відрізком [а; b] (рис. 88).
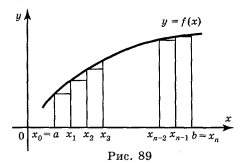 Нехай треба обчислити площу криволінійної трапеції, обмеженої зверху графіком неперервної функції у = f(x), яка приймає додатні значення, з боків відрізками прямих x = а, х = b, знизу відрізком [а; b], який лежить на осі ОХ (рис. 89).
Нехай треба обчислити площу криволінійної трапеції, обмеженої зверху графіком неперервної функції у = f(x), яка приймає додатні значення, з боків відрізками прямих x = а, х = b, знизу відрізком [а; b], який лежить на осі ОХ (рис. 89).
Розіб'ємо відрізок [a; b] на л рівних частин й позначимо абсциси точок поділу через х1, x2 ..., xn-1, a = xo, b = xn: а = xo < х1 <x2 < ... < xn-1 < xn= b.
 На кожному із цих відрізків побудуємо прямокутники, як показано на рисунку 89. Висота прямокутника, побудованого на відрізку [хо, х1], дорівнює уо = f(xo); висота прямокутника, побудовано на відрізку [x1, х2], дорівнює у1 = f(x1) і т. д.; висота прямокутника, побудованого на відрізку [xn-1, хn], дорівнює f(xn-1)·
На кожному із цих відрізків побудуємо прямокутники, як показано на рисунку 89. Висота прямокутника, побудованого на відрізку [хо, х1], дорівнює уо = f(xo); висота прямокутника, побудовано на відрізку [x1, х2], дорівнює у1 = f(x1) і т. д.; висота прямокутника, побудованого на відрізку [xn-1, хn], дорівнює f(xn-1)·
Довжина основи кожного прямокутника дорівнює ![]() . Слід зазначити, що
. Слід зазначити, що
x1 – xo = x2 – x1 = x3 – x2 = …= xn – xn-1 = ![]() x
x
Об'єднання всіх n прямокутників є східчаста фігура. Позначимо її площу через S , тоді
Sn = f(xo) ·Δx + f(x1)·Δx + f(x2)·Δx + ... +f(xn-1)·Δx =(f(xо)+f(x1)+···+f(xn-1))Δx.
Якщо n→![]() , то Δx→ 0 і, оскільки функція у = f(х) неперервна, то східчаста фігура буде все менше відрізнятися від криволінійної трапеції. А тому площа S криволінійної трапеції буде все менше відрізнятися від Sn, тобто Sn
, то Δx→ 0 і, оскільки функція у = f(х) неперервна, то східчаста фігура буде все менше відрізнятися від криволінійної трапеції. А тому площа S криволінійної трапеції буде все менше відрізнятися від Sn, тобто Sn ![]() S. При досить великих п ця наближена рівність справджується з будь-якою точністю. Природно вважати, що Sn при цьому буде наближатися до числа, яке й приймемо за значення площі криволінійної трапеції.
S. При досить великих п ця наближена рівність справджується з будь-якою точністю. Природно вважати, що Sn при цьому буде наближатися до числа, яке й приймемо за значення площі криволінійної трапеції.
Отже, ![]() .
.
Розглянемо деякі приклади:
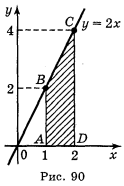
Приклад 1. Обчисліть площу трапеції, обмеженої лініями у = 2х, у=0, х=1, х=2 (рис. 90).
Розв'язання
Площу цієї трапеції можна обчислити за відомою формулою із курсу геометрії
![]() .
.
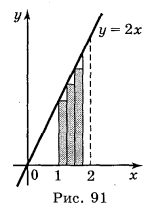
Для обчислення площі цієї трапеції скористуємося способом, який описаний вище. Розіб'ємо відрізок [1; 2] на n рівних частин:
1 = xo < x1 < x2 < ... < хn-1 < хn = 2.
На кожному з цих відрізків (рис. 91) побудуємо прямокутники, як це показано на рисунку. Об'єднання всіх n прямокутників є східчаста фігура, площу якої позначимо через Sn. Тоді ![]()
![]() .
.
У дужках ми одержали суму членів арифметичної прогресії (аn), у якій а1 = 1, d = ![]() , n — число членів, тоді:
, n — число членів, тоді:
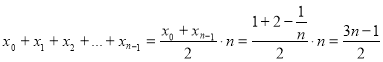 .
.
Таким чином, ![]()
Площа S даної трапеції виражається формулою ![]() .
.
Отже,  .
.
Як бачимо, результати обчислення площі трапеції різними способами співпали.
Відповідь: 3.
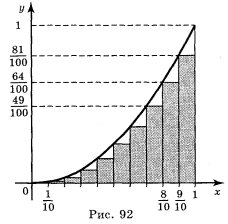 Приклад 2. Обчисліть приблизно площу криволінійної трапеції, обмеженої лініями у = х2, у = 0, x = 1, розділивши відрізок [0; 1] на 10 рівних частин і побудувавши вписану східчасту фігуру із прямокутників (рис. 92).
Приклад 2. Обчисліть приблизно площу криволінійної трапеції, обмеженої лініями у = х2, у = 0, x = 1, розділивши відрізок [0; 1] на 10 рівних частин і побудувавши вписану східчасту фігуру із прямокутників (рис. 92).
Розв'язання
Довжина основи кожного прямокутника дорівнює ![]() ; висоти прямокутників дорівнюють:
; висоти прямокутників дорівнюють: ![]() ,
, ![]() , …,
, …, ![]() або
або ![]() ,
, ![]() , …,
, …, ![]() . Площа східчастої фігури дорівнює:
. Площа східчастої фігури дорівнює:
![]()
![]() = =
= =![]() = 0,285
= 0,285
Площа S криволінійної трапеції приблизно дорівнює 0,285:
Відповідь: " 0,285.
Виконання вправ________________________________
1. Які із заштрихованих на рисунку 93 фігур є криволінійними трапеціями, а які — ні?
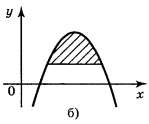
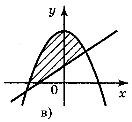

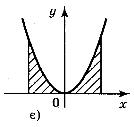
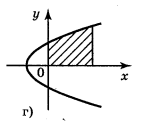
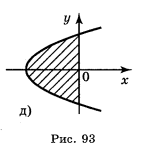
Відповідь: а), г), є) — зображення криволінійних трапецій.
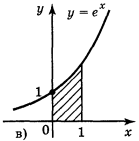
2. Побудуйте криволінійні трапеції:
а) у = x2, x = 1, x = 2, у = 0; б) у = sin х, x = 0, x = π, y = 0;
в) у = е·*", x = 0, x = 1, y = 0; r) y = ![]() , x = 0, x = 4, у = 0.
, x = 0, x = 4, у = 0.
 Відповідь: рис. 94
Відповідь: рис. 94
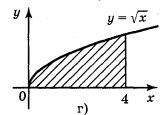
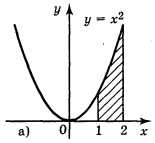
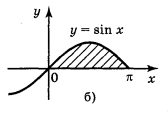
Рис. 94
3. Обчисліть приблизно площу криволінійної трапеції, обмеженої лініями у = 2х''1, х = 0, х = 4, у = 0, розділивши відрізок [0; 4] на чотири рівні частини і побудувавши східчасту фігуру із прямокутників.
Відповідь: 7,5.
4. Обчисліть приблизно площу криволінійної трапеції, обмеженої лініями
у=![]() , x = l, x = 4, y = 0, розділивши відрізок [1; 4] на 6 рівних частин і побудувавши східчасту фігуру із прямокутників.
, x = l, x = 4, y = 0, розділивши відрізок [1; 4] на 6 рівних частин і побудувавши східчасту фігуру із прямокутників.
Відповідь: ![]() 3,186.
3,186.
IV. Сприймання і усвідомлення задачі про знаходження шляху, пройденого тілом.
 Математика вивчає різні зв'язки між величинами. Важливі приклади таких зв'язків дає механічний рух. Ми вже багато разів зверталися до прикладу руху матеріальної точки по осі. Між положенням x(t) (координатою) точки і її швидкістю v(t) існує зв'язок:
Математика вивчає різні зв'язки між величинами. Важливі приклади таких зв'язків дає механічний рух. Ми вже багато разів зверталися до прикладу руху матеріальної точки по осі. Між положенням x(t) (координатою) точки і її швидкістю v(t) існує зв'язок:
v(t) = x’(t).
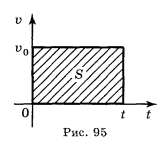
Почнемо знову із задачі про механічний рух. Нехай точка рухається з постійною швидкістю υ = υ0 . Графіком швидкості в системі координат (t; υ) буде пряма υ = υ0, паралельна осі часу t. Якщо вважати, що в початковий момент часу t = 0 точка знаходилась в початку координат, то шлях її s, пройдений за час t обчислюється за формулою s = υ0 t. Величина υ0 t являє собою площу прямокутника, обмеженого графіком швидкості, віссю t і двома вертикальними прямими, тобто шлях точки можна обчислити як площу криволінійної трапеції (рис. 95). Звернемося до випадку нерівномірного руху. Тепер швидкість можна вважати постійною тільки на маленькому проміжку часу.
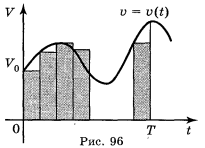 Розіб'ємо проміжок часу (рис. 96) [0;Τ] на n рівних частин
Розіб'ємо проміжок часу (рис. 96) [0;Τ] на n рівних частин ![]() ;
;
0 = t0 < t1 < t2 < ... < tn-1 < tn = Τ,
t1 - t0 = t2 – t1 = …= tn – tn-1 = Δt.
Шлях, пройдений тілом за проміжок часу [tk; t+Δt], де k = 0, 1, ..., n - 1 приблизно дорівнює добутку υ(tk)·Δt, а шлях, пройдений тілом за проміжок часу [0; Τ], приблизно дорівнює
![]() .
.
Якщо n → ![]() , то Δt → 0, і тоді шлях, пройдений тілом за проміжок часу [0; T], який позначимо через S, дорівнює
, то Δt → 0, і тоді шлях, пройдений тілом за проміжок часу [0; T], який позначимо через S, дорівнює ![]() .
.
Отже, S = ![]() .
.
V. Сприймання і усвідомлення поняття інтеграла.
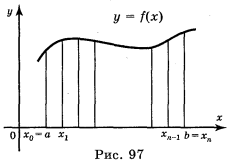 Обидві задачі, які ми розглянули, розв'язувалися одним і тим самим методом, яким розв'язують багато інших задач (знаходження роботи змінної сили, знаходження маси неоднорідного стержня і т. д.). Узагальнемо цей метод. Розглянемо неперервну функцію у = f(x), невід'ємну на відрізку [а; b] (рис. 97). Розіб'ємо відрізок [а; b] на n рівних частин а = x0 < x1 < x2 < … < xn-1 < хn = b, довжина кожної частини дорівнює
Обидві задачі, які ми розглянули, розв'язувалися одним і тим самим методом, яким розв'язують багато інших задач (знаходження роботи змінної сили, знаходження маси неоднорідного стержня і т. д.). Узагальнемо цей метод. Розглянемо неперервну функцію у = f(x), невід'ємну на відрізку [а; b] (рис. 97). Розіб'ємо відрізок [а; b] на n рівних частин а = x0 < x1 < x2 < … < xn-1 < хn = b, довжина кожної частини дорівнює ![]() = Δx.
= Δx.
Утворимо суму S добутків f(xi)·Δx, де і = 0; 1; ... ; n - 1, яка називається інтегральною сумою: Sn = f(xo)·Δx + f(x1)·Δx + f(x2)·Δx + ... + f(xn-1)·δx·.
Знайдемо S = ![]() .
.
За означенням цю границю називають інтегралом функції y = f(x) від a до b і позначають 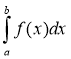 (читають так: «інтеграл від a до b еф від x де ікс»).
(читають так: «інтеграл від a до b еф від x де ікс»).
У позначенні інтеграла все вказує на спосіб його утворення. Знак інтеграла нагадує видовжену латинську букву S — першу букву слова summa (сума). Підінтегральний вираз f(x)dx нагадує вигляд кожного окремого доданка f(x1)·Δx інтегральної суми. Множник dx в математиці називають диференціалом. Число а називається нижньою межею інтегрування, а число b — верхньою межею інтегрування. Таким чином, ![]() =
=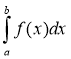 .
.
Отже, 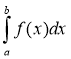 , якщо f(x)
, якщо f(x) ![]() 0 для всіх x є [а;b], являє собою площу криволінійної трапеції обмеженої лініями: у = f(x), x = а, х = b, y = 0.
0 для всіх x є [а;b], являє собою площу криволінійної трапеції обмеженої лініями: у = f(x), x = а, х = b, y = 0.
Виконання вправ
1. Побудуйте схематично фігури, площі яких виражаються такими інтегралами:
a) ![]() ; б)
; б) 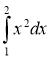 ; в)
; в) 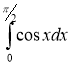 ; r)
; r) ![]() .
.
Відповідь: рис. 98.
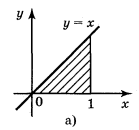
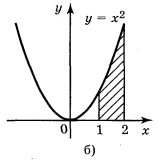
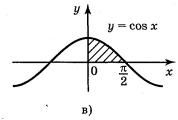
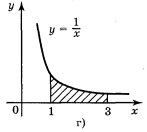
Рис. 98
2. Запишіть за допомогою інтеграла площі фігур, зображених на рисунку 99.
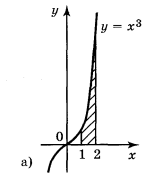
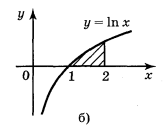
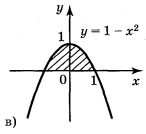
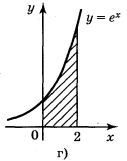
Рис. 99
Відповіді: а)![]() ; б)
; б) 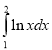 ; в)
; в) 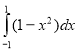 ; г)
; г) ![]()
Слід зазначити, що в означенні інтеграла відрізок [a; b] можна було б ділити на n не обов'язково рівних частин. Але в цьому разі довжина найбільшого з відрізків розбиття повинна прямувати до 0, коли n → ![]() .
.
VI. Підведення підсумків уроку.
VII. Домашнє завдання.
Розділ IX § 4 (1—2). Запитання і завдання для повторення розділу IX № 9, 10.
Знайдіть площу криволінійної трапеції, обмеженої лініями:
у = ![]() ; x = 1, x = 2, у = 0, розбивши відрізок [1; 2] на десять рівних частин і побудувавши східчасту фігуру із прямокутників.
; x = 1, x = 2, у = 0, розбивши відрізок [1; 2] на десять рівних частин і побудувавши східчасту фігуру із прямокутників.
1


про публікацію авторської розробки
Додати розробку
