ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ ФУНКЦІЙ ДО РОЗВ’ЯЗУВАННЯ РІВНЯНЬ

                       

                         Яцейко Галина                                 викладач математики

Херсонський морський фаховий коледж

                                                    Херсонська державна морська академія

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

1.     Вступ  ------------------------------------------------------------------------------- 3

2.     Розділ 1. Врахування області визначення функції ------------------------- 5

     

3.     Розділ 2. Використання поняття множини значень функції при

розв’язуванні рівнянь ------------------------------------------------------------- 9

4.     Розділ 3. Використання монотонності функцій при розв’язуванні

   рівняння ----------------------------------------------------------------------------- 12

5.     Висновок --------------------------------------------------------------------------- 14

6.     Використані джерела ------------------------------------------------------------ 15

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

   Ще у першому тисячолітті до нашої ери давні вавилоняни та єгиптяни вміли розв’язувати рівняння, а у ІХ ст. видатний узбецький математик Мухаммед аль Хорезмі зібрав і систематизував  способи розв’язування рівнянь і написав свій твір «Кітаб ал-джебр ал-мукабела» (книга про відновлення і протиставлення). Що означають ці слова? Назву «ал-джабра» носила операція перенесення членів із однієї частини рівняння в другу, а слово «ал-мукабала» означало зведення подібних доданків. Наприклад, коли при розв’язуванні рівняння 5х + 4 = 2х - 3, ми замінюємо його на 5х - 2х = -3-4, то робимо операцію «ал-джабра», а коли після цього міняємо зліва 5х-2х на 3х, а -3-4 справа на -7, то робимо «алмукабалу» (тепер це називається зведенням подібних доданків). На відміну від слова «ал-джабра», яке трансформувалось в слово «алгебра», про «ал-мукабалу» пам’ятають тільки історики. 

   Велике значення рівнянь підкреслював А. Ейнштейн. Він сказав: «Мені доводилось ділити свій час між політикою і рівнянням. Проте рівняння, на мій погляд набагато важливіші, тому що політика існує тільки для даного часу, а рівняння будуть існувати вічно.” 

   Об’єкт дослідження: взаємозв’язок двох основних предметів вивчення алгебри — рівнянь і функцій.

    Предмет дослідження: процес застосування властивостей функцій як методу розв’язування рівнянь.

    Метою роботи є дослідження методів розв’язування рівнянь, що базуються на властивостях функцій, тобто функціонально-графічного метод

Завдання роботи: 

1)  розглянути теоретичні основи застосування властивостей функцій при розв’язуванні рівнянь; 

2)  проаналізувати використання області визначення, множини значень, монотонності функцій ; 

3)  підібрати систему завдань, при розв’язуванні яких використовуються певні властивості функцій; 

4)  показати на практиці ефективність та переваги функціонального методу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 1

Врахування області визначення функції

   Якщо область допустимих значень (ОДЗ) рівняння (нерівності або системи) складається із скінченного числа значень, то для розв’язування достатньо перевірити всі ці значення

У деяких рівняннях область визначення складається із скінченної кількості точок. Для розв’язання таких рівнянь достатньо перевірити, чи є знайдені числа з області визначення рівняння його коренями.

Приклад:

Розв’язати рівняння:

. 

Розв’язання

ОДЗ рівняння визначається системою:

2x−² −2x1 ≥ 0,   {x²2 ^≥≤ ¹1^,.  

                         {              ₂ ≥ 0;        x

Ця система виконується тільки при x² = 1, тоді x = ±1.

Корені рівняння можуть знаходитись тільки в його ОДЗ, тобто серед чисел x=1 і x = -1.  Перевірка показує, що число 1 є коренем даного рівняння.

Відповідь: 1.

Дослідимо доцільність використання області визначення функції при розв’язуванні рівнянь різних типів.

Рівняння 1.1  

. 

Розв’язання

Знайдемо ОДЗ рівняння:

                              ,        x ,

                                 ,               x ,

            x=2

 , ;       

Перевіркою встановлюємо, що x=2 є коренем рівняння.

Відповідь: 2.

Рівняння 1.2  

. 

Розв’язання

,      x,  ,  x  ,

ОДЗ:     

                                                                                                       ,          ,

;       ; x ⟺ x 

Розглянемо систему нерівностей із змінною x:

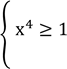
x, x,

,                         x=1

;

x;

x ,

Звідси маємо систему   

.

Отже, y,    

Таким чином, ОДЗ рівняння:   x .

Підставимо x = 1 у рівняння:

 , 

, 

, 

   |y − 1| = −2y + 1 

1)    y ≥ 1, y − 1 = −2y + 1 

         y   

2)    y < 1, 1 − y = −2y + 1

         y = 0 ∈ (−∞; 1) 

Відповідь: x=1, y=0.

Рівняння 1.3

  

                                              x − 3 ≥ 0                         x ≥ 3

ОДЗ: {6 − 2x ≥ 0.        Тоді {x ≤ 3.

Отже, ОДЗ: х=3 – корінь

.

Інших коренів немає, оскільки до ОДЗ входить тільки одне число.

Відповідь: х = 3.

Зауважимо, що в тому випадку, коли ОДЗ заданого рівняння – порожня множина (не містить жодного числа), ми навіть без перевірки можемо дати відповідь, що рівняння не має коренів. Наприклад, якщо потрібно розв’язати рівняння

                                                                                                                                   х − 3 ≥ 0,                 х ≥ 3,

                          5х,то його ОДЗ задається системою {                      тобто {             яка не має

                                                                                                                                   2 − х ≥ 0,                 х ≤ 2,

розв’язків. Отже, ОДЗ заданого рівняння не містить жодного числа, і тому це рівняння не має коренів.

Отже, врахування області визначення передбачає наступний алгоритм:

1) знайти ОДЗ рівняння (якщо ОДЗ не містить жодного числа, то рівняння розв’язків не має); 2) підібрати корінь з ОДЗ; 3) виконати перевірку.

Цей алгоритм значно спрощує розв’язування рівнянь.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Pозділ 2

Використання поняття множини значень функції при

розв’язуванні рівнянь

Одним з ефективних методів розв’язування рівнянь є метод, що ґрунтується на використанні обмеженості функцій. До найбільш відомих обмежених функцій належать тригонометричні функції; функції, що містять модуль, степінь, корінь парного степеня.

Теоретичне обґрунтування даного методу дають наступні теореми.

Теорема 1. Якщо на деякій множині M дійсних чисел справджуються нерівності f(x) ≤ a, φ(x) ≤ b, то на множині M рівняння f(x) + φ(x) = 𝑎 +

𝑏

f(x) = a,

                           рівносильне системі рівнянь   {                   

φ(x) = b.

Теорема 2.    f ²(x) + φ²(x) = 0 ⟺ { ^f(^x) ^{= 0,} φ(x) = 0.

Приклад 1.

Розв’язати рівняння     .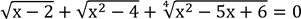

Розв’язання Дане рівняння рівносильне системі

,

                                                                                                       ,     

.

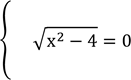З першого рівняння системи маємо x=2, що задовольняє друге і третє рівняння.

Отже, x=2 - розв’язок даного рівняння.

Відповідь: х = 2. 

Приклад 2.

𝑥² − 12𝑥 + 36 + |𝑥² − 4𝑥 − 12| = 0

(𝑥 − 6)² + |𝑥² − 4𝑥 − 12| = 0

     Оскільки, сума двох невід’ємних функцій може дорівнювати нулю тоді і тільки тоді, коли кожен з доданків дорівнює нулю, рівняння 

(𝑥 − 6)

² + |𝑥² − 4𝑥 − 12| = 0 рівносильне системі {|𝑥₂(−𝑥 −4𝑥6−)²12=|0= 0

      З першого рівняння маємо х=6, що задовольняє друге рівняння.

Отже, х = 6 - розв’язок даного рівняння.

Відповідь: х = 6.

Теорема 3.  Якщо f(x) ≥ a, φ(x) ≤ a, то

f(x) = a,

                          f(x) = φ(x) ⟺ {                    

φ(x) = a.

Приклад 1. Розв’язати рівняння     x⁴ + ¹₄ = 2 − (x − 1)². x

Розв’язання

ОДЗ:  x ≠ 0

      У лівій частині рівняння функція f(як сума двох x

взаємно обернених додатних чисел). 

      У правій частині функція  φ(x) = 2 − (x − 1)² ≤ 2. 

x⁴ +  = 2,

За теоремою 3             {          x    2 − (x − 1)² = 2.

      З другого рівняння одержуємо x=1, що задовольняє і перше рівняння системи.

Відповідь: х = 1.

Приклад 2.

  

Запишемо задане рівняння так:

 

 

𝑓,

g) = .

Отже, задане рівняння рівносильне системі

 

Із другого рівняння одержуємо х = 2, що задовольняє й першому рівнянню.

Відповідь: х = 2.

 

 

 

 

 

 

Розділ 3 Використання монотонності функцій при розв’язуванні рівнянь

Теоретичне обґрунтування використання монотонності функцій дають наступні теореми:

Теорема 1. Якщо функція f(x) зростає (або спадає) на деякому проміжку, то рівняння f(x) = a не може мати більше одного кореня на цьому проміжку.

Отже, для розв’язання такого рівняння достатньо показати монотонність функції f(x) та знайти цей корінь методом добору.

Приклад 1.

Розв’язати рівняння     x.

Розв’язання

Функція y  є зростаючою при x ≥ 0 як сума двох зростаючих функцій. Добираємо корінь рівняння:   x = 4.

За теоремою 1 цей корінь – єдиний.

Відповідь: х = 4.

Теорема 2. Якщо на деякому проміжку функція f(x) зростає, а функція g(x) спадає, то рівняння f(x) = g(x) має на цьому проміжку не більше одного кореня.

Приклад 1.

Розв’язати рівняння      .

Розв’язання

Функція f зростає на області визначення,

g- спадає як сума двох спадних функцій.

Тому рівняння може мати лише один корінь. Підбираємо x = 3.

Перевіркою встановлюємо, що це число задовольняє рівняння.

Відповідь: х = 3.

Дослідимо доцільність використання розглянутих теорем для розв’язування нестандартних рівнянь

Приклад 1. 

x⁹ + 3x − 4 = 0. 

Розв’язання

Запишемо рівняння у вигляді x⁹ = −3𝑥 + 4. У лівій частині рівняння зростаюча функція, у правій – спадна. Підбором знаходимо корінь x = 1.

Інших розв’язків рівняння не має.

Відповідь: х = 1.

Приклад 2. 

Розв’яжіть рівняння 𝑥. Якщо рівняння має єдиний коріть,

то запишіть ЙОГО у відповідь. Якщо рівняння має кілька коренів, то у відповідь запишіть БІЛЬШИЙ корінь.

Розв’язання

   Проаналізуємо задане рівняння. Ліва частина заданого рівняння на множині x  є зростаючою функцією як сума зростаючих функцій

f . Тому вона може набути значення 10 лише в одній точці. Підбором встановлюємо, що х = 2 є коренем рівняння. 

Відповідь: х = 2.

 

Висновок

У процесі проведеного дослідження мети роботи досягнуто, завдання виконано і отримано наступні результати і висновки:

1)    розглянуто теоретичні основи застосування властивостей функцій при розв’язуванні рівнянь.;

2)    підібрано систему завдань до кожної із розглянутих властивостей функцій (врахування області визначення, оцінка множини значень, монотонність);

3)    розкрито методику використання функціонального методу на конкретних  прикладах;

4)    доведено, що використання функціонального методу є раціональним та ефективним; він значно спрощує процес розв’язання, а в багатьох випадках є єдино можливим засобом досягнення результату;

5)    функціональний метод розв’язування рівнянь є універсальним, його можна використовувати при розв’язуванні різних типів рівнянь:

раціональних, дробово-раціональних, ірраціональних, тригонометричних.

 

 

 

 

 

 

 

 

Використані джерела

1.     Ю.В. Головчинська “Нестандартні методи розв’язування рівнянь” – Великі Бірки, 2010

2.     Ю.О. Захарійченко, В.К. Репета, І.С. Маркова, В.В. Карпік “МАТЕМАТИКА. Тренувальні матеріали. 2-ге видання” - Київ, 2016

3.     Є.П. Нелін “Алгебра і початки аналізу. Академічний рівень” – Харків, 2010

4.     Б.І. Юрченко “Застосування властивостей функцій до розв’язування рівнянь”

– Кобеляки, 2011