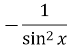конспект уроку "Правила диференціювання"

 

 

 

 

Конспект

 уроку з алгебри

проведеного в 10-А класі

на тему: Правила диференціювання.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  Тема уроку: Правила диференціювання.

  Мета уроку:

  навчальна: працювати над засвоєнням учнями: правил обчислення похідних; змісту основних правил диференціювання та формулювання їх математичною мовою, домогтися свідомого сприйняття учнями змісту понять  «диференційована функція», «диференціальне числення», сформувати вміння знаходити похідні функцій, використовуючи правила знаходження похідних; продовжити формувати вміння та навички учнів застосовувати набуті знання до розв’язування задач з даної теми;

  розвивальна: розвивати логічне  мислення,  комунікабельність, увагу, пам’ять, здатність до самостійності мислення; усне та писемне мовлення; розвивати інтерес до математики;

  виховна: виховувати в учнів бажання мати глибокі й міцні знання, працьовитість та уважність; сприяти розвитку всесторонньо розвинутої особистості;

  Тип уроку: засвоєння нових знань і вмінь

  Обладнання: підручник, конспект по темі уроку, роздатковий матеріал (картки із таблицею похідних елементарних функцій).

План уроку

І. Організаційний момент

II. Перевірка домашнього завдання

III. Актуалізація опорних знань

IV. Мотивація навчальної діяльності на уроці повідомлення теми уроку

V. Пояснення нового матеріалу

VІ. Первине застосування набутих знань, вмінь та навичок

VIІ. Підсумок уроку

VІІІ. Повідомлення домашнього завдання

Хід уроку

  І. Організаційний момент

Вітаюсь з учнями. Перевіряю готовність класу до уроку (чистоту дошки, наявність крейди, ганчірки), з’ясовую хто черговий, відмічаю відсутніх.

  ІІ. Перевірка домашнього завдання

  Домашнє завдання на 16.03.2020 р. за підручником Математика: алгебра і початки аналізу та геометрія, рівень стандарту: підруч. для 10 кл. закладів загальної середньої освіти / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. – Х. : Гімназія, 2018. – 256с. : іл.

Опрацювати §3 п.18, п.19, № 18.2, №18.8.

№18.2

Знайдіть приріст функції f  у точці х₀, якщо: 1) f(x)=4-3х, х₀=1,х=0,3;

                                                                             2) f(x)=0,5х², х₀=-2,х=0,8.

Розв’язання

1) f=f(x)- f(x₀); х= x₀+х=1+0,3=1,3;

f=(4-3х)-( 4-3х₀)=4-3х-4+3х₀=3х₀-3х=31-31,3=3-3,9=-0,9;

2) f=f(x)- f(x₀); х= x₀+х=-2+0,8=-1,2;

f=0,5х²-0,5=0,5(-1,2)²-0,5(-2)²=0,51,44-0,54=0,72-2=-1,28.

№18.8.

  Тіло рухається по координатній прямій за законом s (t) = 5t² (переміщення вимірюють у метрах, час — у секундах). Знайдіть:

1) середню швидкість тіла при зміні часу від t₀ = 1 с до t₁ = 3 с;

2) миттєву швидкість тіла в момент t₀ = 1 с.

Розв’язання

1) = = == = – середня швидкість; = t₁-t₀ = 3-1=2 (c).

(t₀)= 101+2=12 (м/с).

2) (t₀)===;(1)=101=10 (м/с).

ІІІ. Актуалізація опорних знань

1. Дайте означення похідної функції у точці х₀.

(Похідною функції у = f(x) в точці х_о називається границя відно­шення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля, а границя існує, тобто

)

2. Символом  ∆х позначають?  (приріст аргументу)

3. Символом  ∆ƒ, ∆у позначають ?  (приріст функції)

4. Сформулюйте геометричний зміст похідної? (кутовий коефіціент дотичної, проведеної до графіка функції f у точці з абсцисою х₀ , дорівнює значенню похідної функції f у точці х₀, тобто k(х₀)=f’(х₀))

5. Сформулюйте механічний зміст похідної? (якщо y = s (t) — закон руху матеріальної точки по координатній прямій, то її миттєва швидкість у момент часу t₀ дорівнює значенню похідної функції y = s (t) у точці t₀ , тобто v(t₀) = s’(t₀))

  IV. Мотивація навчальної діяльності на уроці повідомлення теми мети уроку

  Людина завжди прагне до комфорту й швидкого отримання результату. Не поїдете ви з Чернігова, наприклад, у Варшаву на велосипеді, чи не так? Це довго й незручно. Швидше за все, дістанетеся потягом, машиною або літаком.

Зазначимо, що похідна кожної функції y=2x-8, y=x³ або y=значно легше обчислити не за визначенням, а за формулами, тож спробуємо сьогодні вивчити таблицю елементарних функцій і правил диференціювання.

  V. Пояснення нового матеріалу

  Розглянемо таблицю похідних елементарних функцій (роздаю кожному на парту таблицю)

f(x)	f'(x)
C (const)	0
x	1
xn	n∙xn-1
	, (x≠0)
	, (x
	, (x≠0)
sin x	cos x
cos x	-sin x
tg x
ctg x

 

 

Ознайомимось із прикладами знаходження похідної різних елементарних функцій.

№19.2

Знайдіть похідну функції: 1) у=х⁴; 2) у=х^-15; 3) у= ; 4) у=.

Розв’язання

1) =(х⁴)=4х^4-1=4х³;

2) =( )=-1 х^-15-1=-15х^-16;

3) =()=х^-17=-17х^-17-1=-17х^-18=;

4) =()===.

№19.6

Продиференціюйте функцію: 1) у=; 2) y=; 3) y=; 4) y= .

Розв’язання

1) =()= ;

2) =()= ()===;

3) =()= ()===;

4) =()= ()= ==.

VІ. Первине застосування набутих знань, вмінь та навичок

  Для знаходження похыдних у складніших випадках доцільно пам’ятати спеціальні правила (правила диференціювання), за якими знаходять похідні від суми, різниці, добутку та частки тих функцій, для яких ми вже знаємо значення похідних, та похідну від складеної функції (функції від функції).

  А тепер запишемо в зошити правила знаходження похідної суми, різниці, добутку й частки фцнкцій. У запису приймемо значення функцій f та g та їх похідних у точках x: f(x₀)=f; g(x₀)=g; f (x₀)=f ; g (x₀)=g.

Правила диференціювання

1. (Cf)=Cf — сталий множник можна виносити за знак похідної.

2. (f±g) =f ±g — похідна суми (різниці) диференційованих функцій дорівнює сумі (різниці) їх похідних.

3. (f∙g)'=f g+gf – похідна добутку.

4. – похідна частки.

№3

Знайдіть похідну функції: 1) у=х⁷+х³; 2) у=х⁸(2х +х⁴); 3) у=.

Розв’язання

(Нагадаємо, що алгебраїчний вираз (чи формулу, яув задає функцію) називають за результатом останньої дії, яку потрібно виконати при знаходженні значення заданого виразу. Отже, у завданні 1 спочатку потрібно знайти похідну суми: (f+g) =f + g, у завданні 2 – похідну добутку: (f∙g)'=f g+gf, а в завданні 3 – похідну частки: . У завданнях 1 і 2 слід використати формулу (хⁿ)= nx^n-1, а в завданні 2 врахувати, що при обчисленні похідної від 2х постійний множник 2 можна винести за знак похідної. У завданні 2 краще спочатку розкрити дужки, а потім узяти похідну суми).

1) =(х⁷+х³)=(х⁷)+ (х³)= 7х⁶+3х².

2) =(х⁸(2х +х⁴))= (х⁸)(2х +х⁴)+(2х +х⁴) х⁸.

Ураховуючи, що (х⁸)=8х⁷;

                            (2х +х⁴)= (2х)+(х⁴)=2х+4х³=2+4х³,

маємо =8х⁷(2х +х⁴)+( 2+4х³) х⁸= 16 х⁸+8х¹¹+2 х⁸+4х¹¹=18 х⁸=12х¹¹.

3) =()=.

Ураховуючи, що (х+2)=х+2=1+0=1, (5-х)=5-х=0-1=-1,

маємо ===.

VIІ. Підсумок уроку

Час уроку добігає кінця, тому підведемо підсумки. Перевіримо, що ви за-пам’ятали за урок.

 Фронтальне опитуванння:

1. Як знайти похідну суми, добутку, частки двох функцій?

2. Назвіть формулу знаходження похідної степеневої функції хⁿ.

VІІІ. Повідомлення домашнього завдання

  Ви сьогодні добре попрацювали й домоглися успіху. А щоб закріпити свій успіх – одержуєте домашнє завдання.

Опрацювати §3 п.19, п.20, №19.7, №20.2(1,3), №20.4(3,4), №20.6(2,4) та вивчити табличку похідних елементарних  функцій.

(учні відкривають щоденники та записують домашнє завдання)

 

 

16 березня

Домашня робота

№19.7

Продиференціюйте функцію: 1) у=; 2) y=; 3) y= .

Розв’язання

1) =()= ;

2) =()= ()===;

3) =()= ()= ==.

№20.2 (1,3)

Знайдіть похідну функції: 1) у=2х⁵-х; 3) у=-3sin x+2cos x.

Розв’язання

1) =(2х⁵-х)=(2х⁵)- (х)= 10х⁴-1;

3) =(-3sin x+2cos x)=(-3sin x)+ (2cos x)=-3cos x-2sin x.

№20.4(3,4)

Знайдіть похідну функції: 3) у=х⁴cos x; 4) у=x tg x.

Розв’язання

3) =( х⁴cos x)=( х⁴)(cos x)+(cos x) х⁴=4x³cos x- х⁴sin x;

4) =( x tg x)=( х)( tg x)+x( tg x) = tg x +.

№20.6(2,4)

Знайдіть похідну функції: 1) у=; 4) у=.

Розв’язання

3) =()===;

4)=()==.