Проектна робота "Моделювання і розрахунок розміру сільськогосподарського підприємства"

 

Проектна  робота групи учнів 10 класу

 

 

 

 

 

 

Моделювання і розрахунок розміру сільськогосподарського підприємства

 

 

 

	Керівник роботи: Шептур Галина Євгенівна, учитель математики

 

ЗМІСТ
ВСТУП	4
РОЗДІЛ 1 ПОСТАНОВКА ЗАДАЧІ	6
1.1 Основні поняття та напрями дослідження	6
1.2 Апарат диференціального та інтегрального числення для побудови математичних моделей	7
РОЗДІЛ 2 МОДЕЛЮВАННЯ СІЛЬСЬКОГОСПОДАРСЬКОГО ПІДПРИЄМСТВА З МАКСИМАЛЬНИМ ПРИБУТКОМ	10
2.1   Обчислення загальних витрат сільськогосподарського виробництва	10
2.2   Прибуток сільськогосподарського підприємства	10
2.3 Визначення оптимальних розмірів сільськогосподарського підприємства	11
ВИСНОВКИ	17
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	18

 

 

ВСТУП

 

Математичні методи широко використовуються в різних галузях людської діяльності. Однією з найважливіших областей застосування математики є економіка. Математичне моделювання є важливим інструментом дослідження економічних процесів і об’єктів з метою побудови правильної політики і прийняття оптимальних рішень як на рівні окремих підприємств, так і на глобальному рівні. Розглянемо один з прикладів математичної моделі, на основі якої плануються розміри сільськогосподарського підприємства.

Об’єкт дослідження – сільськогосподарське підприємство.

Предметом дослідження є моделювання і розрахунок розміру сільськогосподарського підприємства.

Мета дослідження – змоделювати і розрахувати розмір сільськогосподарського підприємства, при якому його прибуток буде максимальним.

Об’єкт, предмет, мета дослідження обумовили наступні його завдання:

- ознайомитись із літературою за темою;

- розібрати нові математичні поняття: границя функції, похідні функції вищих порядків, невизначений та визначений інтеграли;

- встановити загальні витрати сільськогосподарського виробництва;

- обчислити чистий економічний прибуток сільськогосподарського підприємства;

- дослідити оптимальні розміри сільськогосподарського підприємства;

- зробити висновки.

Основними методами дослідження стали: опанування й осмислення літератури за темою, методи моделювання та оптимізації, синтез, співставлення і аналіз даних.

 

РОЗДІЛ 1 

ПОСТАНОВКА ЗАДАЧІ

 

1.1  Основні поняття та напрями дослідження

Під сільськогосподарським розуміємо таке підприємство [2], яке здійснює свою основну діяльність у вигляді вирощування (виробництва й переробки) сільськогосподарської продукції. Прикладами сільськогосподарських підприємств можна вважати: тваринницьку ферму разом із землею, на якій вирощується корм для тварин; цукровий завод разом із землею, на якій вирощується цукровий буряк, тощо. Під розміром сільськогосподарського підприємства розуміємо площу оброблюваних земель (площу оранки). Критерієм оптимізації розміру сільськогосподарського підприємства є максимізація його прибутку.

Отже, визначимо розмір сільськогосподарського підприємства,  при якому прибуток підприємства буде максимальним. Оптимальний розмір сільськогосподарського підприємства залежить від багатьох факторів. Зокрема, такі фактори, як використання високопродуктивної техніки, упровадження передових технологій вирощування і переробки сільськогосподарської продукції, поліпшення організації праці сприяють збільшенню розмірів господарства. Однак у результаті розширення площі оброблюваних земель значно зростають витрати на доставку вирощеної продукції на підприємство для переробки (ферма, цукровий завод тощо). Таким чином, транспортні витрати обмежують розміри господарства.

Розглянемо математичну модель сільськогосподарського підприємства, яка дозволить встановити його оптимальні розміри, виходячи з обмежень в результаті транспортних витрат. У моделі єдиним цілим є оброблювані землі і підприємство для переробки сільськогосподарської продукції. У зв’язку із цим умовно поділимо сільськогосподарське виробництво на три складові: 1) отримання первинної сільськогосподарської продукції (вирощування сільськогосподарських культур); 2) її доставка на підприємство для переробки; 3) переробка первинної сільськогосподарської продукції й отримання вторинної продукції (м'ясо, молоко, цукор тощо). У розділі 2 обчислимо загальні витрати сільськогосподарського виробництва, знайдемо прибуток сільськогосподарського підприємства та встановимо оптимальні розміри сільськогосподарського підприємства, виходячи з умови максимізації прибутку.

 

1.2 Апарат диференціального та інтегрального числення для побудови математичних моделей

Розглянемо поняття границі [1]. Кажуть, що змінна величина у деякому процесі прямує до кінцевої границі , якщо величина є постійною і у цьому процесі необмежено наближається до . Тоді записують

(lim – з латинської «limes», що означає границя).

Таким чином, кінцевою границею змінної величини, якщо вона існує, є величина постійна. Відповідно до даного визначення нескінченно малі величини – це величини, що прямують до нуля, тобто мають границею нуль. Нескінченно ж великі величини кінцевої границі не мають.

Якщо говорити, « необмежено наближається до » – це все одно, що сказати «різниця між та необмежено наближається до нуля», тобто є нескінченно мала. Останню рівність можна записати у вигляді

Змінна величина може прямувати до своєї границі , залишаючись менше за неї, тобто зі сторони менших значень, тоді умовно записують

(це, звичайно, умовний запис, адже ).

Якщо у процесі прямування до залишається більшим за , то пишуть . Нарешті, може прямувати до , то будучи більшим, то меншим за .

Розглянемо похідну функції [1]. Нехай задана функція . Тоді швидкість її зміни, що відноситься до одиниці зміни аргументу, при значенні аргументу дорівнює

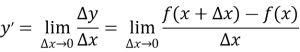
Ця швидкість називається похідною, що взята від змінної за змінною . Іншими словами, похідна – це границя приросту функції до приросту аргументу, коли останній прямує до нуля. З огляду на те, що при різних значеннях указана швидкість (якщо говорити взагалі) є різною, то похідна представляє собою нову функцію від , яку прийнято позначати .

Похідні вищих порядків. Нехай . Тоді похідна називається похідною першого порядку. Вона у свою чергу є функцією і тому від неї можна взяти похідну, яка називається похідною другого порядку від вихідної функції:

Аналогічно визначається похідна третього порядку

і наступні за нею.

Розглянемо функцію і будемо вважати, що як вона сама так і її похідна не мають розривів. З того, що  , випливає, що функція зростає у кожному інтервалі, в якому її похідна додатна. Іншими словами, якщо швидкість зміни якої-небудь величини додатна, то ця величина зростає, а якщо швидкість від’ємна, то величина спадає. Так як похідна при неперервному переході від додатних значень до від’ємних, має пройти через нульове значення, то точки, в яких інтервал зростання змінюється на інтервал спадання мають власну назву. Точки, в яких похідна дорівнює нулю, називаються стаціонарними. Стаціонарні точки і точки, в яких похідна першого порядку не існує, називаються критичними. З метою встановлення того, чи є дана критична точка точкою екстремуму (екстремальною точкою), необхідно проводити дослідження. Наприклад, якщо похідна при переході через критичну точку змінює знак, то така критична точка є точкою екстремуму, якщо знак похідної не змінюється, то точка, що розглядається, не є екстремальною. Можна також скористатись для дослідження і другою похідною.

Інтегрування [1]. Нехай функція є похідною від функції , тобто  ; тоді називають первісною функцією для . Наприклад, функція є похідною від , а є первісною для . Взагалі основна задача диференціального числення – це задача про знаходження похідної, основна задача інтегрального числення – це задача про знаходження первісної для заданої функції. Звернемо увагу, що будь-яка задана функція має не одну первісну, наприклад, , але і . Отже, будь-які дві первісні однієї і тієї ж самої функції відрізняються одна від одної на постійний доданок. Сукупність усіх первісних для функції називається невизначеним інтегралом від функції і позначається . Таким чином, якщо , то і навпаки. Іншими словами, невизначений інтеграл – це загальна первісна, яка містить довільну константу, при кожному численному значенні якої отримуємо частинну первісну.

При розв’язанні багатьох задач стає потреба сумувати нескінченно велику кількість нескінченно малих доданків. Це приводить до одного з центральних понять математики – поняттю визначеного інтеграла. Наприклад, нехай необхідно обчислити площу криволінійної трапеції, що обмежена прямими  ,  ,    та графіком функції  .

Якщо розбити увесь інтервал змін для на маленькі проміжки за допомогою точок ділення  і прийняти висоту на кожному з цих малих проміжків постійною, то отримаємо наближений вираз для площі криволінійної трапеції

,     де    ( ,     ).

Геометричний зміст правої частини – це площа ступінчатої фігури, що зображена на рис. 1.1 і отримана у результаті заміни кожного з    стовпчиків, на які розбита криволінійна трапеція, прямокутником з тією ж основою і з висотою, що дорівнює однієї з висот стовпчика. За граничного переходу, при нескінченному подрібненні розбиття, отримаємо

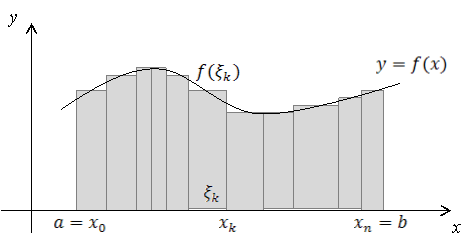
Рис. 1.1  Площа криволінійної трапеції

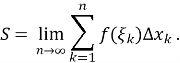
Як нам відомо, границя, до якої прямує інтегральна сума

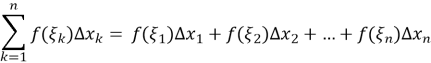
при нескінченому подрібненні проміжків розбиття, називається визначеним інтегралом від функції за інтервалом інтегрування і позначається

 

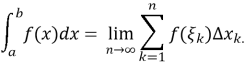
РОЗДІЛ 2 

МОДЕЛЮВАННЯ СІЛЬСЬКОГОСПОДАРСЬКОГО ПІДПРИЄМСТВА З МАКСИМАЛЬНИМ ПРИБУТКОМ

 

2.1 Обчислення загальних витрат сільськогосподарського виробництва

Загальні витрати сільськогосподарського виробництва [3] запишемо у вигляді суми трьох доданків , і :

                                      ,                         (1)

кожен з яких виражає загальні витрати відповідної складової сільськогосподарського виробництва. Розглянемо окремо кожен з доданків.

Припустимо, що загальні витрати на вирощування певної сільськогосподарської культури пропорційні площі посіву :

                                                                              (2)

де – загальні витрати на вирощування сільськогосподарської культури на одиницю площі.

Припустимо також, що загальні витрати на переробку первинної сільськогосподарської продукції пропорційні повній масі вирощеної продукції , а в підсумку – площі посіву:

                                                     (3)

де – загальні витрати на переробку одиниці маси первинної сільськогосподарської продукції, – урожайність сільськогосподарської культури.

Обчислимо загальні витрати на транспортування сільськогосподарської продукції з поля на підприємство для переробки . З метою спрощення розрахунків виберемо форму поля у вигляді кільця з внутрішнім і зовнішнім радіусами. Вважатимемо, що підприємство для переробки продукції розташоване в центрі кола (рис. 1.2). Для обчислення величини дане коло розіб’ємо на достатньо вузьких кілець концентричними колами, радіуси яких задовольняють умовам: (рис. 2.2). Розглянемо довільне -те кільце, внутрішній радіус якого дорівнює , а зовнішній . Припустимо, що ширина цього кільця значно менша від його зовнішнього радіуса, тобто

                                                .                           (4)

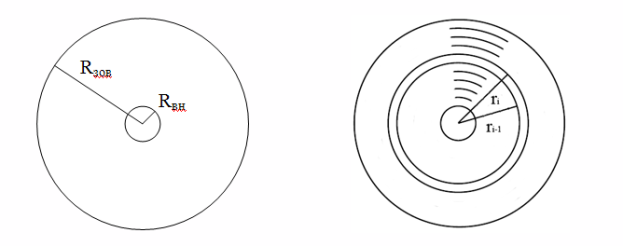
Рис. 2.1  Площа поля                           Рис. 2.2 Концентричні кола

Площа -го кільця дорівнює:        

.              (5)

Остання наближена рівність у формулі (5) буде тим точнішою, чим краще виконуватиметься нерівність (4). Обчислимо далі повну масу продукції, зібраної в -му кільці:             

   ,                (6)

і знайдемо вартість транспортування цієї продукції на підприємство для переробки. Для простоти припустимо, що доставка продукції з будь-якої точки -го кільця відбувається за відрізком прямої, яка з’єднує дану точку (в якій продукція зібрана) з центром кола – підприємством для переробки. Довжина цього відрізка наближено дорівнює зовнішньому радіусу кільця . У цьому випадку повна вартість транспортування всієї продукції з -го кільця на підприємство для переробки (повні витрати на транспортування) наближено дорівнює:

             ,         (7)

де – вартість транспортування одиниці маси вантажу на одиницю відстані.

Для визначення загальних витрат пов’язаних із транспортуванням сільськогосподарської продукції на підприємство для переробки зі всього поля необхідно підсумувати загальні витрати за всіма кільцями, від 1 до :

   .         (8)

Як відомо, ця сума являє собою інтегральну суму функції на проміжку . У граничному випадку нескінченно великої кількості розбивок кола () такого, що , дана сума дорівнює визначеному інтегралу від функції  у межах від до :

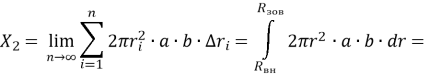
Отже, у рамках даної моделі загальні витрати на транспортування сільськогосподарської продукції на підприємство для переробки дорівнюють:

При підстановці співвідношень (2), (3) та (10) у формулу (1) з урахуванням того, що площа поля дорівнює , отримаємо формулу для обчислення загальних витрат сільськогосподарського виробництва:

 

 

 

 

2.2  Прибуток  сільськогосподарського  підприємства

Обчислимо чистий економічний прибуток , який сільськогосподарське підприємство отримає в результаті продажу своєї кінцевої  продукції (м'ясо, молоко, цукор тощо) [5]. Величину   визначимо  з формули:

де – загальний прибуток сільськогосподарського підприємства. Величина дорівнює добутку маси проданої кінцевої сільськогосподарської продукції  на ціну одиниці її маси :

Величину можна виразити через величину повної маси вирощеної продукції (3), а тому через розміри поля співвідношенням

де коефіцієнт c дорівнює масі кінцевої продукції, отриманої з одиниці маси первинної продукції (наприклад, масі цукру у тоннах, отриманого з тонни цукрових буряків). Підставивши співвідношення (14), (13) і (11) у (12), отримаємо величину чистого економічного прибутку як функцію розмірів поля:

 

2.3  Визначення оптимальних розмірів сільськогосподарського підприємства

Знайдемо оптимальні розміри сільськогосподарського підприємства [4] (радіус поля) з позиції максимально можливого значення чистого економічного прибутку (15). Для цього дослідимо функцію  на екстремум за змінною при незмінному значенні .  Похідна функції дорівнює:

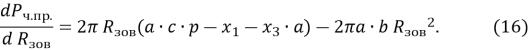
Прирівнявши похідну до нуля і розв’язавши рівняння відносно, знайдемо можливу точку екстремуму

Друга похідна функції   в точці дорівнює

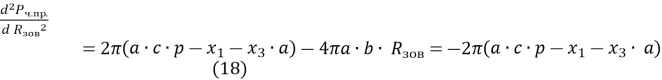
і є меншою за нуль. Тому у точці маємо максимум функції  .

У той же час переконуємося, що функція не має екстремуму за змінною . При цьому максимального значення величина досягає при .

 

Підставивши у формулу (15) , а також значення (17), отримаємо максимально можливу величину чистого економічного прибутку сільськогосподарського підприємства

Нехай у формулі (15) . Тоді чистий економічний прибуток дорівнює:

 

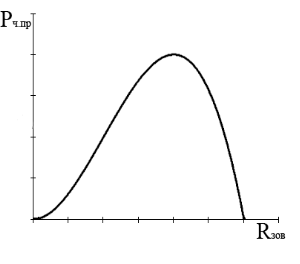
Схематичний графік даної функції представлений на рис. 2.3. Із графіка і формули (20) випливає, що прибуток сільськогосподарського підприємства є від'ємним, тобто підприємство становиться збитковим, якщо зовнішній радіус поля перебільшуватиме критичне значення , тобто Це пояснюється тим, що прибуток, отриманий від збільшення оброблюваної площі в цьому випадку не компенсує витрати на транспортування вирощеної сільськогосподарської з більш віддалених дільниць на підприємство для переробки.

 

 

ВИСНОВКИ

У даній роботі було розглянуто один із прикладів математичної моделі, на основі якої планувались розміри сільськогосподарського підприємства. Задля цього сільськогосподарське виробництво умовно було поділено на три складові: 1) отримання первинної сільськогосподарської продукції (вирощування сільськогосподарських культур); 2) її доставка на підприємство для переробки; 3) переробка первинної сільськогосподарської продукції й отримання вторинної продукції (м'ясо, молоко, цукор тощо). На основі даного розподілу було записано формулу загальних витрат сільськогосподарського виробництва, обчислено чистий економічний прибуток цього підприємства:

та досліджено оптимальні розміри сільськогосподарського підприємства, а саме:

   Описана модель є спрощеною. Вона не враховує такі фактори, як реальна форма поля, наявність доріг від поля на підприємство для переробки тощо. Але в той же час вона висвітлює характерний вплив транспортних витрат на прибуток і вказує на існування оптимального, а також критичного розмірів сільськогосподарського підприємства.

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1.               Мышкис А.Д. Лекции по высшей математике. – М.: Наука, 1972.
2.               Гудак В. В. Організаційно-економічни механізм забезпечення дохідності сільськогосподарського виробництва: суть та особливості / В. В. Гудак // Сталий розвиток економіки. – 2011. - № 2. – С.73-77.
3.               Огійчук М. Ф. Суть прибутку та підходи до методики його визначення / М. Ф. Огічук // Економіка АПК. – 2009. - № 6. – С. 31-45.
4.               Романова Т. В. Чинники, що впливають на збільшення прибутку підприємств України у сучасних умовах / Т. В. Романова // Електронне наукове фахове видання "Ефективна економіка". – 2015. - №4 [Електронний ресурс] – Режим доступу до ресурсу:

http://www.economy.nayka.com.ua/?op=1&z=3976

5.               Зубков Д. О. Планування підвищення прибутковості діяльності підприємства в ринкових умовах / Д. О. Зубков // Руснаука. – 2010. [Електронний ресурс]. – Режим доступу:

http://www.rusnauka.com/36_PWMN_2010/Economics/76729.doc.htm