Методична розробка "Застосування властивостей функцій до розв'язування ірраціональних рівнянь"

Застосування властивостей функцій

до розв'язування ірраціональних рівнянь

           Усе частіше в літературі зустрічаються рівняння, розв'язування яких стандартними способами важке, громіздке або неможливе. Тоді можна спробувати використовувати властивості функцій. Іноді такий підхід приводить до більш простого і раціонального розв'язання Досить часто знання властивостей функцій, що входять у рівняння допомагає знаходити їх розв’язки.

Отож, розглянемо такі властивості функцій, що входять в рівняння як його складові, які б привели до нестандартного їх розв’язування та продемонструємо їх практичне застосування.

1. Область допустимих значень

             У випадку, коли задано рівняння , спільна область визначення для функцій і називається областю допустимих значень (ОДЗ) цього рівняння. Зрозуміло, що кожен корінь заданого рівняння входить як до області визначення функції  так і до області визначення функції .  Отже, кожен корінь рівняння обов’язково входить до ОДЗ цього рівняння. Це дозволяє в деяких випадках за рахунок аналізу ОДЗ одержати розв’язки рівняння.

Приклад 1.   Розв’язати рівняння[V1][V2]:

 Розв'язання

 ОДЗ: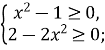  

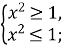
Перевірка:

– корінь, 

– не корінь, 

 Відповідь. 1.

 Розглядуваний приклад дозволяє виділити орієнтир для розв'язування аналогічних рівнянь:

            Якщо область допустимих значень (ОДЗ) рівняння складається із скінченного числа значень, то для розв’язування досить перевірити всі ці значення.

 У тому випадку, коли ОДЗ – порожня множина ( не містить жодного числа), ми можемо зразу дати відповідь, що задане рівняння не має коренів. Тому перед безпосереднім розв’язанням рівняння, потрібно його проаналізувати, прослідкувати за поведінкою окремих членів рівняння для допустимих значень невідомої змінної.

Приклад 2.         Розв’язати рівняння

Розв’язання.

ОДЗ:     

           Отже, ОДЗ заданого рівняння не містить жодного члена, і тому це рівняння не має коренів.

 Відповідь: рівняння розв’язку не має.

Приклад 3.            Розв’язати рівняння

Розв’язання.

ОДЗ:    .

         Область допустимих значень для змінної x складається тільки з числа 2. Легко перевірити, що х = 2 – корінь рівняння.

Відповідь:  2.

Приклад 4.            Розв’язати рівняння

Розв’язання.

ОДЗ:  

           Підстановкою кінцевих точок проміжку ОДЗ впевнюємося, що корінь, а не являється коренем заданого рівняння.

Нехай    Тоді очевидно,  що

          Одержано, що ліва частина заданого рівняння більша правої, тому рівняння коренів за зазначеної умови не має.

Відповідь: 

2. Оцінка лівої та правої частин рівняння (область значень функції)

        Деякі рівняння можна розв’язати за допомогою оцінки лівої та правої частин рівняння.

 Сутність методу оцінки – у використанні оцінки значень обох частин рівняння з метою переходу до рівносильної системи рівняння або обґрунтування відсутності коренів.

Даний прийом базується на такій властивості: нехай потрібно розв’язати рівняння виду і з’ясувалося, що то рівність між лівою і правою частинами можлива тоді і тільки тоді, коли і одночасно дорівнюють а. Тобто якщо

то  

Узагальнюючи теоретичне положення методу оцінки до різних видів ірраціональних рівнянь, доходимо висновку:

               1. Рівняння C.

Не має розв’язку, якщо:

2. Рівняння

2.1. Не має розв’язку, якщо:

          2.2. Рівносильне системі рівнянь

 якщо

Наведемо приклади розв’язання рівнянь.

Приклад 1. Розв’язати рівняння

Розв’язання.

Оцінюємо  ліву частину заданого рівняння

тому  що суперечить умові заданого рівняння.

Відповідь: рівняння коренів не має.

Приклад 2. Розв’язати рівняння

Розв’язання.

Оцінюємо праву і ліву частину заданого рівняння

     тому що

Отже, задане рівняння рівносильне системі рівнянь

                .

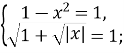
Відповідь: 0.

Приклад 3. Розв’язати рівняння

Розв’язання.

ОДЗ:   

Позначимо ,  g

Здійснимо оцінку кожної із введених функцій.

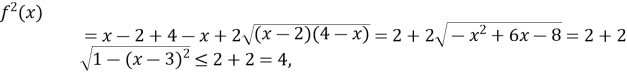
Тому

g

Рівність досягається, якщо

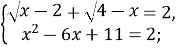
         Число є коренем другого рівняння системи, воно задовольняє і перше рівняння цієї ж системи рівнянь.

Відповідь:

Примітка.  Оцінити ліву частину заданого рівняння можна застосовуючи нерівність Коші-Буняковського:

  тоді

Приклад 4. Розв’язати рівняння

  Розв’язання.

Оцінюємо ліву частину заданого рівняння.

Рівність досягається за умови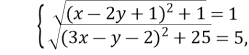

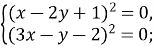
Відповідь:  

3. Використання зростання та спадання функцій

 В даному випадку спрацьовує така схема розв'язування:

● підбираємо один чи кілька коренів рівняння;

● доводимо, що інших коренів немає, при цьому використовуючи теореми про корені рівнянь або оцінку значень лівої та правої частини рівнянь.      

                                Теореми про корені рівняння

Теорема 1

у

           Якщо в рівнянні f(x) = а функція  f(x)

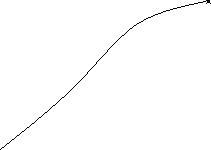                                                                 зростає (спадає) на даному проміжку

     у = а             у = f(x)                             то це рівняння може мати не більше

                                                                 ніж один корінь на цьому проміжку.

                 Функція неперервна.

 х

Теорема 2

             y=q(x) y=f(x)                 Якщо в рівнянні f(x) = q(x) функція f(x)       

                                                                 зростає  на деякому проміжку, а  q(x) -              

              а                                                 спадає на цьому самому проміжку (або 

                                                                 навпаки), то це рівняння може мати не      

                                                                 більше ніж один корінь на цьому     

                                                      х         проміжку. Обидві функції неперервні.      

       Справді , якщо функція монотонна, то таке рівняння має лише один корінь, бо для монотонної функції нерівним значенням аргументу відповідають нерівні значення функції. Графічно це означає, що пряма лінія, паралельна осі абсцис (графік функції – константи), не може перетинати графік монотонної функції більше, ніж в одній точці.

 Якщо – кусково-монотонна функція, то рівняння може мати не тільки більш як один корінь, але навіть нескінченне їх число, коли має нескінченне число проміжків монотонності. Проте їх не може бути більше, ніж число проміжків монотонності кусково-монотонної функції.

Приклад 1. Розв’язати рівняння

Розв’язання.

ОДЗ:  

Нехай gабсциса цієї параболи ,  тому функція на проміжку є зростаючою.  Так як функція   зростає на проміжку, а, значить , задане рівняння на області визначення має єдиний корінь

Відповідь: 

Приклад 2. Розв’язати рівняння

Розв’язання.

ОДЗ:  

Помножимо і поділимо ліву частину заданого рівняння на вираз

одержимо

спадає, а– зростає на області визначення, тому задане рівняння має не більше одного кореня. Шляхом добору, одержимо.

Відповідь: 

Приклад 3. Розв’язати рівняння

Розв’язання.

ОДЗ:  

Помножимо ліву та праву  частини заданого рівняння на вираз

a)

Ліва частина рівняння являє собою спадну функцію, а права – зростаючу.

Перевіркою встановлено, що числа  -2 та 1 – корені заданого рівняння.

Відповідь: -2; 1.

Приклад 4. Розв’язати рівняння

Розв’язання:

          ОДЗ: .   Функція    зростаюча, і при

Функція спадна на області допустимих значень, при

набуває найменшого значення – єдиний корінь.

Відповідь: 243.

Приклад 5. Розв’язати рівняння

                                       -

Розв’язання.

ОДЗ:

Записуємо рівняння дещо в іншому вигляді

             Функція є спадною на області визначення. Функція – зростаюча, але   - спадаюча на області визначення, тому функція  теж є спадною на ОДЗ.

Тому задане рівняння може мати не більше одного кореня.

Оскільки тому число 2 є коренем  заданого рівняння.

Відповідь: 2.

            Отже, застосування властивостей функцій  до розв’язування ірраціональних рівнянь на практиці сприяє розвитку критичного мислення здобувачів освіти, дозволяє на практиці показати внутрішньо предметні зв’язки, важливість кожної теми та поповнить скарбничку прийомів учнів нетрадиційними підходами, які можна використовувати в майбутньому. 

[V1]

[V2]