Розв'язання тригонометричних рівнянь методом розкладання на множники

Розкладання на множники.

Нехай маємо рівняння f(х) = 0, ліву частину якого можна розкласти на множники  ∙ f₂(x) ∙...∙ f_n(x) = 0.
  Оскільки добуток кількох множників дорівнює нулю, коли дорівнює нулю хоча б один із множників, то далі необхідно лише розв’язати кожне з рівнянь f₁(х) = 0; f₂(x) = 0...f_n(x) = 0 і перевірити отримані корені на предмет входження їх в область допустимих значень початкового рівняння.
  Нехай D_i ,i ∈ ℕ – область допустимих значень функції f_i(x) та D – ОДЗ функції f(х).Тоді

D= D₁ ∩…… ∩ D_n.

Позначемо X як множину коренів рівняння f(х) = 0.Тоді X_i i ∈ ℕ

-множина розв'язків рівняння f_i(х).Враховуючи все вищезазначене, отримаємо

X=( X₁ ∪ X₂ ∪ ….. ∪ X_n ) ∩ (D₁ ∩…… ∩ D_n ).

Приклад 1.   2x+2x-sin x = 1.

Розв’язання.Для початку зробимо так,щоб у правій частині нашого рівняння вийшов нуль.

                  2x+2x-sin x - 1= 0.

Ліву частину нашого рівння позначимо f(x).

f(x)= 2x+2x-sin x – 1.

Область визначення цієї функції-множина дійсних чисел.

Запишемо нашу функцію у вигляді добутку,використовуючи формули,які представлені у Додаток 1.

             f(x)= 2x+2x-sin x – 1=(2x- sin x)+(2x-1)=sin x(2x-1)+[2(1-x)-1]=sin x(2x-1)+(1-2x)= sin x(2x-1)- (1-2x) = (2x-1)( sin x-1).

Тепер наше рівнння набуває вигляду

(2x-1)( sin x-1)=0

Коренями даного рівняння будуть всі корені даної сукупності

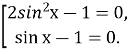
Коренями першого рівння сукупності будуть числа,які задовольняють найпростійші тригонометричні рівняння:sin x= або sin x= -.У першрму випадку

x=(-1)ⁿ arcsin + πn = (-1)ⁿ   + πn, n ∈ ℤ.

У іншому випадку

x=(-1)^k arcsin )+ πk = (-1)^k+1   + πk, k ∈ ℤ.

Об’єднання отриманих розв’язків

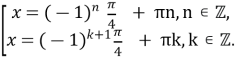⟺ l, l∈ ℤ,

дають корені рівняння .

Коренями другого рівняння сукупності будуть числа

.

Об’єднання коренів

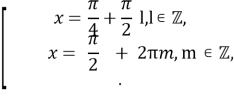
дасть нам розв’язки тригонометричного рівняння 2x+2x-sin x = 1.