Тригонометричні нерівності з параметром.

Тригонометричні нерівності з параметром.

Параметри у тригонометрії зустрічаються  при розв’язуванні тригонометричних рівнянь, нерівностей та їх систем.

Не існує загального методу розв’язування задач з параметрами у тригонометрії. Відповідний метод розв’язування кожної задачі залежить від її характерних особливостей.

Можна визначити наступні вміння при розв’язуванні задач з параметрами:

1)    вміти бачити природний хід розв’язування тригонометричних нерівностей;

2)    вміти розв’язувати алгебраїчні нерівності з параметрами;

3)    знати властивості квадратичної функції і умови розміщення її коренів на числовій осі;

4)    мати навички побудови та перетворення графіків функцій і не забувати про графічні способи розв’язання задач;

5)    пам’ятати, що |cosα |≤1,|sinα |≤1.

Розглянемо приклади:

1.При якому найменшому значенні параметра а нерівність має хоча б єдиний розв’язок?

Отже розглянемо такі випадки:

1 Випадок: а

Якщо а , то скористаємось наступними нерівностями:

;

.

Додавши ці нерівності,отримаємо,що

-1=-,

Тому при а < -1 нерівність не матиме розв'язків.

             2 Випадок: а

Якщо а

2.При яких значеннях параметра а нерівність arcsin x + arccos (a-x) має розв’язок?

аrcsin x + arccos (a-x)

arcsin x

Скористаємось тотожністю arcsin x + arccos x=Отримаємо arcsinxarcsin (a-x)

Так як функція у=arcsin x монотонно зростає на всій області визначення,то остання нерівність рівносильна системі нерівностей:

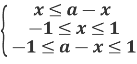
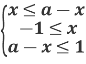
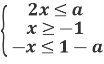
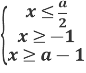
Потрібно розглянути питання взаємного розміщення на числовій прямій точок

 -1 ; ; а-1.

Отже, остання система має рішення , тоді і тільки тоді коли:

Тобто           

При -2аrcsin x + arccos (a-x)  матиме розв'язок.