Методичні матеріали для практичного заняття "Ряди"
РЯДИ
Практичне заняття
Розв’язування задач на ряди
Мета. Знати означення числового ряду, часткової суми ряду, збіжного ряду, необхідну та достатні ознаки збіжності числових рядів, мати поняття про знакозмінні та абсолютно та умовно збіжні числові ряди, знати ознаку Лейбніца та вміти досліджувати на збіжність числові ряди, використовуючи необхідну та достатні умови збіжності. Знати означення функціонального ряду, області збіжності функціонального ряду, степеневого ряду, знати означення ряду Тейлора та Маклорена, вміти розкладати елементарні функції в ряд Тейлора і Маклорена, знати означення тригонометричного ряду, ряду Фур’є, вміти розкладати простіші функції в ряд Фур’є.
Теоретичні відомості
Найпростіші властивості рядів
|
Завдання 1
- Знайти загальний член ряду:
а)![]()
б) ![]()
в) ![]()
- Записати перших п’ять членів ряду та перевірити необхідну умову збіжності ряду:
а) ![]()
б) ![]()
в) ![]()
Теоретичні відомості
Достатні умови збіжності знакододатніх рядів
|
то при
|
Для знакочергових рядів має місце достатня
ознака збіжності Лейбніца
|
Якщо в знакочерговому ряду |
Завдання 2
1. Дослідити на збіжність ряд за ознакою Даламбера:
а) ![]()
б) 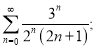
в) 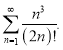
2. Дослідити на збіжність ряд з використанням радикальної ознаки Коші:
а) 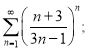
б) 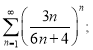
в) 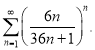
3. Дослідити на збіжність ряд, використовуючи інтегральну ознаку Коші:
а) ![]()
б) ![]()
в) ![]()
4. Записати перших шість членів ряду та дослідити його на збіжність:
а) 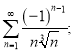
б) 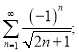
в) ![]()


про публікацію авторської розробки
Додати розробку