Презентація "Визначений інтеграл та його застосування"
Про матеріал
Презентація допоможе учням розвинути вміння застосовувати інтеграл до знаходження площ плоских фігур. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





![Визначений інтеграл, його фізичний та геометричний зміст Визначений інтеграл функції f на відрізку [a; b] позначають 𝒂𝒃𝒇𝒙ⅆ𝒙 (читають: «інтеграл від a до b еф від ікс де ікс»). Отже, 𝒂𝒃𝒇𝒙ⅆ𝒙=𝑭𝒃−𝑭𝒂 (1), де F — довільна первісна функції f на відрізку [a; b] Нехай F — первісна функції f на проміжку I, числа a і b, де a < b, належать проміжку I. Різницю F(b) – F(a) називають визначеним інтегралом функції f на відрізку [a; b]. Визначений інтеграл, його фізичний та геометричний зміст Визначений інтеграл функції f на відрізку [a; b] позначають 𝒂𝒃𝒇𝒙ⅆ𝒙 (читають: «інтеграл від a до b еф від ікс де ікс»). Отже, 𝒂𝒃𝒇𝒙ⅆ𝒙=𝑭𝒃−𝑭𝒂 (1), де F — довільна первісна функції f на відрізку [a; b] Нехай F — первісна функції f на проміжку I, числа a і b, де a < b, належать проміжку I. Різницю F(b) – F(a) називають визначеним інтегралом функції f на відрізку [a; b].](/uploads/files/1179621/302551/329569_images/5.jpg)

![Формула Ньютона-Лейбніца 𝒂𝒃𝒇𝒙ⅆ𝒙=𝑭𝒃−𝑭𝒂 Для обчислення визначеного інтеграла 𝑎𝑏𝑓𝑥ⅆ𝑥 за формулою Ньютона—Лейбніца потрібно: 1) знайти будь-яку первісну F функції f на відрізку [a; b]; 2) обчислити значення первісної F у точках x = b і x = a. 3) знайти різницю 𝐹𝑏−𝐹𝑎. Під час обчислення визначених інтегралів різницю F(b) – F(a) позначають 𝐹𝑥𝑎𝑏. Формула Ньютона-Лейбніца 𝒂𝒃𝒇𝒙ⅆ𝒙=𝑭𝒃−𝑭𝒂 Для обчислення визначеного інтеграла 𝑎𝑏𝑓𝑥ⅆ𝑥 за формулою Ньютона—Лейбніца потрібно: 1) знайти будь-яку первісну F функції f на відрізку [a; b]; 2) обчислити значення первісної F у точках x = b і x = a. 3) знайти різницю 𝐹𝑏−𝐹𝑎. Під час обчислення визначених інтегралів різницю F(b) – F(a) позначають 𝐹𝑥𝑎𝑏.](/uploads/files/1179621/302551/329569_images/7.jpg)
![Формула Ньютона—Лейбніца дає змогу встановити зв’язок між визначеним інтегралом і площею S криволінійної трапеції, обмеженої графіком функції y = f (x) та прямими y = 0, x = a і x = b (a < b). Використовуючи теорему 1, можна записати:𝑆=𝑎𝑏𝑓𝑥ⅆ𝑥 Ця рівність виражає геометричний зміст визначеного інтеграла. Зауважимо, що в наведеній формулі розглядаються неперервні функції f, які на відрізку [a; b] набувають тільки невід’ємних значень. Формула Ньютона—Лейбніца дає змогу встановити зв’язок між визначеним інтегралом і площею S криволінійної трапеції, обмеженої графіком функції y = f (x) та прямими y = 0, x = a і x = b (a < b). Використовуючи теорему 1, можна записати:𝑆=𝑎𝑏𝑓𝑥ⅆ𝑥 Ця рівність виражає геометричний зміст визначеного інтеграла. Зауважимо, що в наведеній формулі розглядаються неперервні функції f, які на відрізку [a; b] набувають тільки невід’ємних значень.](/uploads/files/1179621/302551/329569_images/8.jpg)
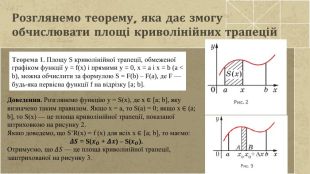
![Розглянемо теорему, яка дає змогу обчислювати площі криволінійних трапецій. Теорема 1. Площу S криволінійної трапеції, обмеженої графіком функції y = f(x) і прямими y = 0, x = a і x = b (a < b), можна обчислити за формулою S = F(b) – F(a), де F — будь-яка первісна функції f на відрізку [a; b]. Доведення. Розглянемо функцію y = S(x), де x ∈ [a; b], яку визначено таким правилом. Якщо x = a, то S(a) = 0; якщо x ∈ (a; b], то S(x) — це площа криволінійної трапеції, показаної штриховкою на рисунку 2. Якшо доведемо, що S’R(x) = f (x) для всіх x ∈ [a; b], то маємо: 𝜟𝑺 = S(𝒙𝑶 + 𝜟𝒙) – S(𝒙𝑶). Отримуємо, що 𝛥𝑆 — це площа криволінійної трапеції, заштрихованої на рисунку 3. Розглянемо теорему, яка дає змогу обчислювати площі криволінійних трапецій. Теорема 1. Площу S криволінійної трапеції, обмеженої графіком функції y = f(x) і прямими y = 0, x = a і x = b (a < b), можна обчислити за формулою S = F(b) – F(a), де F — будь-яка первісна функції f на відрізку [a; b]. Доведення. Розглянемо функцію y = S(x), де x ∈ [a; b], яку визначено таким правилом. Якщо x = a, то S(a) = 0; якщо x ∈ (a; b], то S(x) — це площа криволінійної трапеції, показаної штриховкою на рисунку 2. Якшо доведемо, що S’R(x) = f (x) для всіх x ∈ [a; b], то маємо: 𝜟𝑺 = S(𝒙𝑶 + 𝜟𝒙) – S(𝒙𝑶). Отримуємо, що 𝛥𝑆 — це площа криволінійної трапеції, заштрихованої на рисунку 3.](/uploads/files/1179621/302551/329569_images/9.jpg)
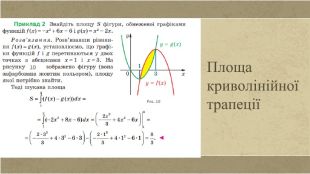
![Обчислення площ плоских фігур Якщо функції f і g є неперервними на відрізку [a; b] і для всіх x ∈ [a; b] виконується нерівність f(x)≥g(x), то площу S фігури, яка обмежена графіками функцій f і g та прямими x = a і x = b, можна обчислити за формулою:𝑺=𝒂𝒃𝒇𝒙−𝒈(𝒙)ⅆ𝒙 Обчислення площ плоских фігур Якщо функції f і g є неперервними на відрізку [a; b] і для всіх x ∈ [a; b] виконується нерівність f(x)≥g(x), то площу S фігури, яка обмежена графіками функцій f і g та прямими x = a і x = b, можна обчислити за формулою:𝑺=𝒂𝒃𝒇𝒙−𝒈(𝒙)ⅆ𝒙](/uploads/files/1179621/302551/329569_images/10.jpg)
![Нехай площина x = x0 перетинає тіло Ф по фігурі з площею S(x0), а проекцією тіла Ф на вісь абсцис є відрізок [a; b] (рис. 8). Якщо y = S(x) — неперервна на відрізку [a; b] функція, то об’єм тіла Ф можна обчислити за формулою𝑽=𝒂𝒃𝑺(𝒙)ⅆ𝒙 Якщо в результаті обертання навколо осі абсцис фігури, обмеженої графіком неперервної та невід’ємної на відрізку [a; b] функції f і прямими x = a, x = b, y = 0, утворюється тіло об’єму V (наприклад: рисунок 9), то𝑽=𝝅𝒂𝒃𝒇𝟐(𝒙)ⅆ𝒙 Обчислення об’ємів тіл обертання Нехай площина x = x0 перетинає тіло Ф по фігурі з площею S(x0), а проекцією тіла Ф на вісь абсцис є відрізок [a; b] (рис. 8). Якщо y = S(x) — неперервна на відрізку [a; b] функція, то об’єм тіла Ф можна обчислити за формулою𝑽=𝒂𝒃𝑺(𝒙)ⅆ𝒙 Якщо в результаті обертання навколо осі абсцис фігури, обмеженої графіком неперервної та невід’ємної на відрізку [a; b] функції f і прямими x = a, x = b, y = 0, утворюється тіло об’єму V (наприклад: рисунок 9), то𝑽=𝝅𝒂𝒃𝒇𝟐(𝒙)ⅆ𝒙 Обчислення об’ємів тіл обертання](/uploads/files/1179621/302551/329569_images/11.jpg)