Тема 1: Найпростіші тригонометричні нерівності

Мета: вивчити основні методи розв’язання тригонометричних нерівностей, пояснити розв’язання цих нерівностей за допомогою тригонометричного кола.

Література: [10] c. 126-133, [3] c. 137-146.

Методичні рекомендації

Нерівність називається тригонометричною, якщо вона містить змінну тільки під знаком тригонометричної функції.

Наприклад, sin 3x > 1,  cos x + tg x < 1 — тригонометричні нерівності.

Розв'язати тригонометричну нерівність означає знайти множину значень змінної, при яких нерівність виконується.

Розв'язування тригонометричних нерівностей зводиться до розв'язування нерівностей:

sin x > a,     sin x < a,     sin x a,      sin x а,

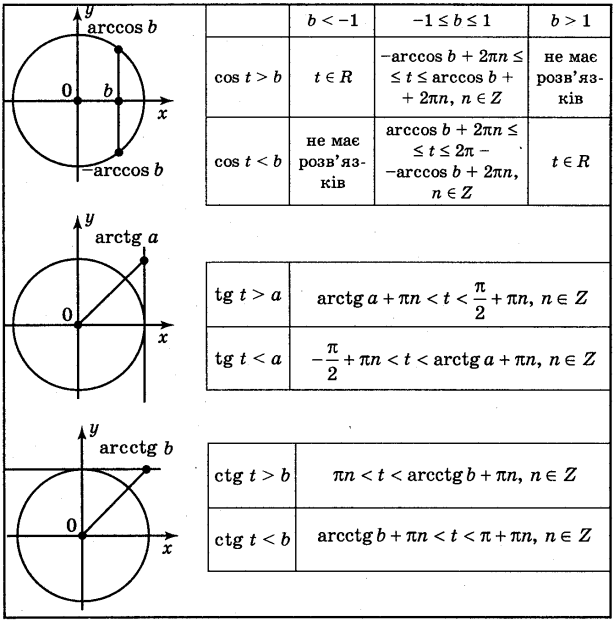
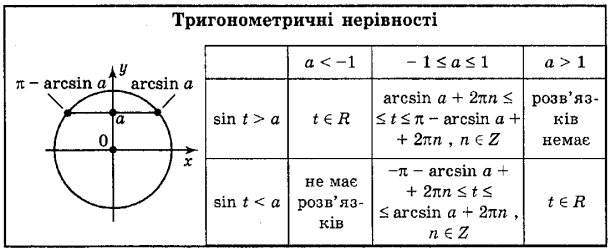
cos x > a,    cos x < a,    cos x a,     cos x a,

tg x > a,     tg x < a,     tg x a,      tg x a, які називаються найпростішими. Найпростіший способ розв’язання тригонометричні нерівності - використання одиничного кола.

Приклади розв’язання тригонометричних нерівностей.

1. Розв'яжіть нерівність sin t .

Розв'язання

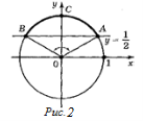
Будуємо одиничне коло (рис. 2) та пряму у = , яка перетинає одиничне коло в точках А і В. Знаходимо на одиничному колі точки, значення ординат яких не менші .

Цими точками є точки дуги АСВ, де А = , В = . Отже, розв'язком нерівності будуть усі значення t із проміжку . Враховуючи, що період функції sin t дорівнює 2π, маємо розв'язок даної нерівності

.

Відповідь:

2. Розв'язати нерівність cost > .

Побудуємо одиничне коло (рис. 4) та пряму х = , яка перетинає одиничне коло в точках А і В. Точки одиничного кола, абсциси яких більші за , лежать на дузі АР₀В, де А = , В = . Отже, розв'язком нерівності будуть усі значення t із проміжку 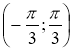. Враховуючи періодичність, маємо:                Відповідь:

3.Розв'яжіть нерівність tg t 1.

Розв'язання

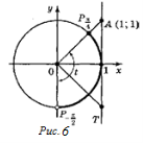
Побудуємо одиничне коло та лінію тангенсів (рис. 6). На осі тангенсів позначимо число 1. Якщо t є розв'язком нерівності, то ордината точки Т, рівна tg t, повинна бути не більша 1. Множина таких точок Т — промінь AT. Множина точок , що відповідають точкам променя АТ, — дуга , яка на рисунку виділена. (Зверніть увагу: точка належить, а точка не належить множині розв'язків). Отже, розв'язком нерівності будуть усі значення t із проміжку . Враховуючи, що період функції tg t дорівнює π, маємо розв'язок даної нерівності , n Z. Відповідь: , де n Z.

4. Розв'яжіть нерівність ctgt -.

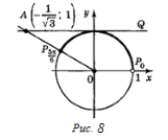На осі котангенсів позначи­мо число і множину (рис. 8) значень котангенсів, не менших за - (промінь AQ). На одиничному колі множина точок, що відповідають кутам, котангенс яких не менший від -, є дуга   Отже, розв'язки нерівності будуть усі значення t із проміжку . Враховуючи періодичність, маємо: , п Z.

Відповідь: , де п Z.

Питання для самоконтролю

1. Яка нерівність називається тригонометричною?
2. Що означає розв’язати тригонометричну нерівність?
3. Які тригонометричні нерівності називаються найпростішими?
4. Який метод використовується для розв’язання тригонометричних нерівностей?

Завдання для самоконтролю

1. Розв’язати нерівності:sin t -; cos x ;  tg t > -; ctgt .

2. Розв'яжіть нерівності:

а) 2sin – ;             б) 2sin l;    

в) 3ctg > – ;       г) sin 1