Автор:                       Л.М. Костенко – спеціаліст вищої категорії, викладач-методист,

Державного вищого навчального закладу «Київський енергетичний коледж»

 

 

 

 

 

 

 

 

 

 

Костенко Л.М. Застосування похідної для дослідження раціональних та трансцендентних функцій і побудови їх графіків. Методичні рекомендації до практичного заняття з навчальної дисципліни «Елементи вищої математики» – Київ, 2020. – 22 с.: іл.

 

 

 

Матеріал методичних рекомендацій містить достатню кількість прикладів на допомогу сту- дентам коледжів в опануванні теоретичного матеріалу, дозволить розширити та поглибити знання студентів з даної теми, навчити їх раціональним прийомам дослідження функцій та побудови їх графіків. Наприкінці кожного розділу наводяться приклади для самоперевірки, а також у розділі 7 запропоновано 30 варіантів для практичної роботи «Побудова графіків дробово-раціональної функції».

 

 

 

 

Розглянуто і схвалено на засіданні циклової предметної комісії природничо-математичних дисциплін (ЦПК № 2) Державного вищого навчального закладу «Київський енергетичний коледж». Протокол від «___» __________ 2020 р. № ______

 

Голова ЦПК ________ Л.М. Костенко

 

 

 

 

 

 

 

 

 

©Костенко Л.М. ©ДВНЗ «КЕК»

 

 

Зміст

 

Анотація................................................................................................................... 3

1  Асимптоти............................................................................................................ 4

2  Використання методу інтервалів для знаходження інтервалів   ............................

знакосталості функції та її похідних........................................................................ 8

  2.1 Знаходження інтервалів знакосталості функції................................................ 8

  2.2 Знаходження інтервалів знакосталості першої та   другої похідних функції... 9

3  Пошук областей розташування графіка функції................................................ 12

4  Загальна схема дослідження функцій і побудови їх графіків............................. 15

5  Дослідження дробово-раціональних функцій та побудова їхніх   .........................

графіків.................................................................................................................. 15

6  Дослідження трансцендентних функцій та побудова їхніх графіків.................. 18

7  Завдання для практичної роботи  «Побудова графіків дробово-   раціональної функції»............................................................................................................................... 21

Літературні джерела............................................................................................... 22

 

 

 

2

 

 

Анотація

 

Мета даних методичних рекомендацій така:

-            допомогти студентам опанувати теоретичний матеріал із використанням достатньої кількості прикладів;

-            розширити та поглибити знання студентів з даної теми;

-            навчити студентів раціональним прийомам дослідження функцій та побудови їх графіків, зокрема, використанню методу інтервалів при знаходженні інтервалів знакосталості, як функції, так і її похідних.

На першому курсі студенти навчалися досліджувати та будувати графіки алгебраїчних функцій, а саме многочленів 𝑦 = 𝑎₀𝑥^𝑛 + 𝑎₁𝑥^𝑛−1 + ⋯ + 𝑎_𝑛−1𝑥 + 𝑎_𝑛, де 𝑥 ∈ 𝑅, тобто функція існувала на всій множині дійсних чисел.

На другому курсі студенти продовжують цю роботу, але вже для такого класу алгебраїчних функцій як дробово-раціональні функції, а також вчаться досліджувати алгебраїчні функції, тобто трансцендентні функції. Такі функції, на відміну від многочленів, існують не при всіх дійсних значеннях незалежної змінної х, а також можуть поводити себе особливо на нескінченності та в околі деяких точок.

Це приводить до вивчення такого поняття як асимптоти.

До того ж дослідження таких функцій носить громіздкий характер. Спростити дослідження допоможе метод інтервалів.

У роботі пропонується знайти асимптоти перед використанням похідної. Це дає можливість на початку роботи у сукупності зі знаннями про точки перетину графіка функції з координатними осями та інтервали знакосталості функції вказати області на координатній площині, в яких будуть знаходитися частини графіка функції.

Наприкінці кожного розділу наводяться приклади для самоперевірки, а та-

кож пропонується 30 варіантів для практичної роботи з даної теми.

 

3

1. Асимптоти

 

Означення 1 Асимптотою графіка функції 𝑦 = 𝑓(𝑥) або кривої називають

таку пряму l, для якої відстань від точки (х; у) графіка функції до прямої l прямує до нуля, коли 𝑥 → ±∞ або 𝑦 → ±∞.

 

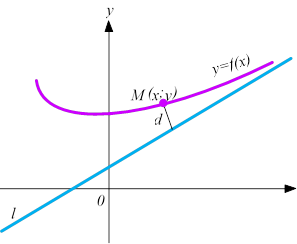Або асимптота графіка функції із нескінченними вітками – це пряма, до якої точка кривої необмежено наближається при віддаленні у нескінченність:

𝑑 → 0 або lim 𝑑 = 0

𝑥→∞

 

Існують три види асимптот:

-            вертикальні; _x

-            горизонтальні;

-            похилі асимтоти.

 

 

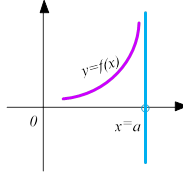
Означення 2 Пряма х=а називається вертикальною асимптотою, якщо має місце рівність:

 

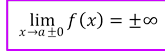
Іншими словами, наявність вертикальної асимптоти характеризує поведінку функції поблизу або в околі точки х=а при наближенні аргумента х як зліва від нуля (𝑥 → 𝑎 − 0), так і справа від нуля (𝑥 → 𝑎 + 0). Зокрема:

 

                                y                                                                                y

 x

           

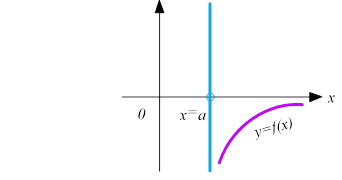
∞ ∞ 𝑥𝑥

 

 

4

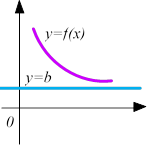
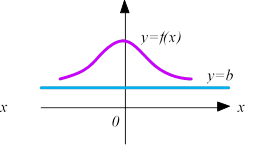
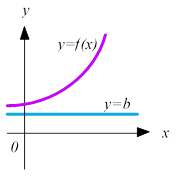
Означення 3 Пряма х=а називається горизонтальною асимптотою, якщо має місце рівність:

 

                                                              lim 𝑓(𝑥) = 𝑏

                                                            𝑥→±∞

 

Наявність горизонтальної асимптоти характеризує поведінку функції при достатньо великих або дуже малих значеннях аргумента х, тобто при 𝑥 → ±∞.  Зокрема:

 

lim 𝑓(𝑥) = 𝑏 𝑥→−∞

lim 𝑓(𝑥) = 𝑏 𝑥→+∞

lim 𝑓(𝑥) = 𝑏 𝑥→±∞

                        y                                                                y

Означення 4 Пряма 𝑦 = 𝑘𝑥 + 𝑏 називається похилою асимптотою, де 

 

𝑓(𝑥) 𝑘 = lim                            𝑥⟶∞      𝑥

𝑏 = lim (𝑓(𝑥) − 𝑘(𝑥)) = 𝑏 𝑥→∞

 

 

                                                 y                                                                                  𝑀𝑃               𝑑

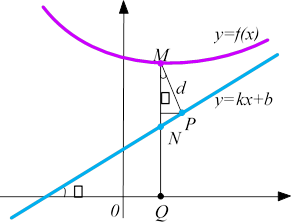Нехай d=MP, тоді 𝑀𝑁 = = . cos 𝜑 cos 𝜑

За означенням 1 lim 𝑑 = lim 𝑀𝑃 = 0.

                                                                                                                                                                    𝑥→∞              𝑥→∞

Якщо lim 𝑀𝑃 = 0, то і lim 𝑀𝑁 = 0 й

                                                                                                                                       𝑥→∞                                      𝑥→∞

навпаки. Проте, 𝑀𝑁 = 𝑀𝑄 − 𝑄𝑁 = 𝑓(𝑥) − (𝑘𝑥 + 𝑏) = 𝑓(𝑥) − 𝑘𝑥 − 𝑏. Отже, lim (𝑓(𝑥) − 𝑘𝑥 − 𝑏) = 0 або

𝑥→∞

𝑓(𝑥) − 𝑘𝑥 − 𝑏 = 𝛼(𝑥) – нескінченно мала величина. Знайдемо з останньої

                                                                                                           ^x     рівності k і b:

 𝑘 = 𝑓(𝑥) − 𝑏+𝛼(𝑥)_{, так як} lim 𝑏+𝛼(𝑥) = 0,

                                                                                                                                     𝑥                  𝑥                          𝑥→∞        𝑥

то 𝑘 , так як lim 𝛼(𝑥) = 0, то 𝑏 = lim (𝑓(𝑥) − 𝑘𝑥)

                   𝑥→∞     𝑥                                                                                     𝑥→∞                                                𝑥→∞

 

5

 

 

 Якщо k або b нескінченні, то похилих асимптот немає,

при k=0, 𝑏 = lim 𝑓(𝑥), а це – горизонтальна асимптота.

𝑥→∞

 

Приклади на знаходження асимптот.

 

1

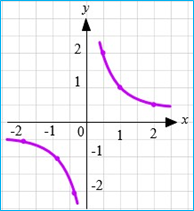
Приклад 1.1 𝑦 =  

𝑥

 

Це відома зі шкільного курсу гіпербола.

𝐷, отже х = 0 – верти-

𝑥→±0 𝑥

кальна асимптота.

𝑦 ≠ 0, так як , до того ж .

𝑥𝑥→±∞ 𝑥

Отже, у = 0 (сама вісь ОХ) – горизонтальна асимптота.

Похилої асимптоти немає.  

 

1

Приклад 1.2 𝑦 =  + 2

𝑥−3

 

Рекомендація: Для знаходження вертикальної асимптоти потрібно знаменник формули функції прирівняти до нуля і розв’язати утворене рівняння відносно х.

 

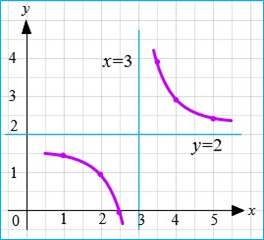𝑥 − 3 = 0 ⟺ 𝒙 = 𝟑 – вертикальна асимптота.

Дійсно, ,

                                                                                                                                                𝑥→3−0    𝑥−3

, до того ж 𝑥 = 3 – 

𝑥→3+0              𝑥−3 точка розриву ІІ-го роду, так як 𝑥 = 3 ∉ 𝐷(𝑦).

Для      знаходження        горизонтальної  асимптоти обчислимо lim 𝑓(𝑥):

𝑥→∞

             

lim ( + 2) = lim + lim 2 = 0 + 2 = 2 𝑥→∞ 𝑥 − 3 𝑥→∞ 𝑥 − 3 𝑥→∞

Отже, 𝒚 = 𝟐 – горизонтальна асимптота. Похилої асимптоти немає.

6

 

Приклад 1.3 

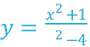𝑥

 

𝑥² − 4 = 0 ⟺ 𝑥⟺ 𝒙 𝟐– вертикальні асимптоти. Обчислимо 

 𝑓

                        𝑥→                      𝑥→       𝑥→

Отже, у = 1 – горизонтальна асимптота. Похилої асимптоти немає.

 

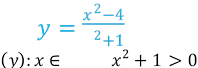                      Приклад 1.4                                 

𝑥

Так як 𝐷  𝑅, бо  при всіх 𝑥 𝑅, то точок розриву немає, а отже немає вертикальної асимптоти.

𝑥

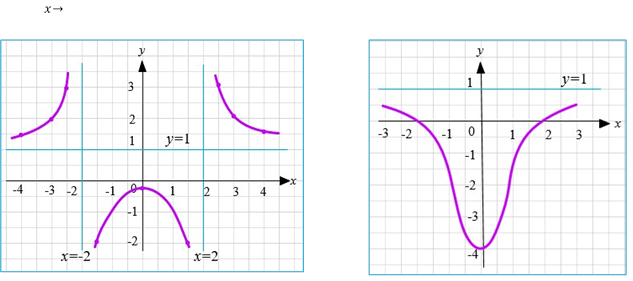
 ⟹ 𝒚 = 𝟏 – горизонтальна асимптота.

                                Графік до прикладу 1.3                                           Графік до прикладу 1.4

 

𝑙𝑛𝑥

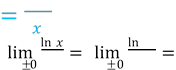
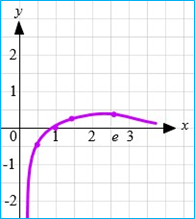
Приклад 1.5 у

′ 𝑥

                       𝐷 ⟹ 𝑥→          𝑥           𝑥→          𝑥_′

 

𝑥

Отже, 𝒙  𝟎 – вертикальна асимптота.

 ⟹ 𝒚 = 𝟎 – горизонта-

                        𝑥→   𝑥           𝑥→ 𝑥

льна асимптота.

Похилої асимптоти нема.  

 

7

 

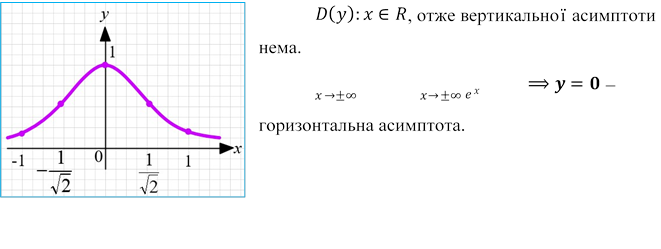
Приклад 1.6 𝑦 = 𝑒^−𝑥2 (крива Гауса)

Зауваження: при обчисленні границі в прикладах 1.5 та 1.6 використовується правило Лопіталя.

 

Приклади для самоперевірки

 

2 1)      𝑦 = 2−1 𝑥 𝑥−2 2)      𝑦 =      𝑥+4 𝑥 3)      𝑦 =

𝑥2+2𝑥−1 𝑦 =        𝑥 7) 𝑦 = 𝑒𝑥 𝑒𝑥𝑡

1+𝑥2 2𝑥2+𝑥+3 4)       𝑦 =      𝑥+6 𝑥2−1 5)       𝑦 =      4 𝑥

8) 𝑥 9)      𝑦 = arctg 𝑥 ln𝑥 10)  𝑦 =   𝑥

 𝑦 =

2. Використання методу інтервалів для знаходження інтервалів 

знакосталості функції та її похідних

2.1. Знаходження інтервалів знакосталості функції

 

Для знаходження інтервалів знакосталості функції будемо використовувати метод інтервалів, який базується на властивості неперервної функції зберігати свій знак у проміжку між точками 𝑥₁, 𝑥₂, … , 𝑥_𝑛 , в яких функція перетворюється в нуль.

8

 

Ті проміжки, в яких 𝑦 > 0, графік функції розташований над віссю (ОХ),

проміжки, в яких 𝑦 < 0, дають розташування графіка функції під віссю (ОХ).

 

𝑥2

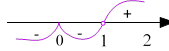
Приклад 2.1 𝑦 =  

𝑥−1

 

𝑥 = 0 – двократний корінь чисельника.

𝑥 = 1 – корінь знаменника.

22 при 𝑥 = 2, 𝑦 =  = 4 > 0, отже, «змійку» проводимо справа і зверху, при

2−1

переході через точку 𝑥 = 0 змійка не перетинає вісь (ОХ), а залишається там, де і була зверху або знизу.

 х

 

Отже, при 𝑥 < 1, 𝑦 < 0, графік функції знаходиться під віссю (ОХ), при всіх 𝑥 > 1, 𝑦 > 0 – графік над віссю (ОХ).

 

𝑥²+2𝑥−1 𝑥

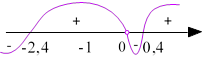
Приклад 2.2 𝑦 =  

Знайдемо корені чисельника: 𝑥² + 2𝑥 − 1 = 0

𝑥

𝑥₁ ≈ −2,4, 𝑥₂ ≈ 0,4 – корені чисельника,

𝑥 = 0 – корінь знаменника,

при 𝑥  

х

 

 

Отже, при ∀𝑥 ∈ (−∞; −2,4) ∪ (0; 0,4)  𝑦 < 0, а при ∀𝑥 ∈ (−2,4; 0) ∪ (0,4; +∞), 𝑦 > 0.

 

2.2. Знаходження інтервалів знакосталості першої та другої похідних функції.

 

Відомо, що за допомогою першої похідної знаходять інтервали монотонності функції, а за допомогою другої похідної шукають інтервали опуклості й точки перегину.

Приклад 2.3 Знайти проміжки монотонності та опуклості функції 

𝑦 =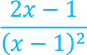  

Знайдемо першу похідну функції:

                                         2𝑥 − 1     ^′          (2𝑥 − 1)^′ ∙ (𝑥 − 1)² − (2𝑥 − 1) ∙ ((𝑥 − 1)²)^′

𝑦_′  

 

2𝑥

= − (𝑥 − 1)₃

 

Знайдемо критичні точки І-го роду. По-перше це 𝑥 = 1, точка в якій не існують як функція, так і перша похідна.

По-друге це точки, в яких похідна дорівнює нулю:

𝑦^′ = 0 ⟺ 𝑥 = 0 – критична точка І-го роду; при 𝑥  

Відкладемо критичні точки на числовій прямій і проведемо «змійку»

справа і знизу, проходячи через корені чисельника (𝑥 = 0) і знаменника (𝑥 = 1).

 

х

-

Таким чином інтервали зростання там, де 𝑦^′ > 0, а саме (0; 1) та інтервали спадання функції там, де 𝑦^′ < 0, тобто (−∞;0) і (1; +∞). Знайдемо другу похідну функції 𝑦^′′:

′′                             2𝑥         ^′                              𝑥          ^′                    𝑥^′ ∙ (𝑥 − 1)³ − 𝑥 ∙ ((𝑥 − 1)³)^′        

𝑦    

 

 

Знайдемо критичні точки ІІ-го роду:

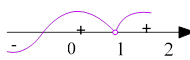
𝑦^′′ = 0 ⟹ 2𝑥 + 1 = 0 ⟹ 𝑥 = − , а також 𝑥 = 1 – парної кратності. При 𝑥 = 2,

𝑓′′

                                                                    12        х

 

при ∀𝑥 < −1 графік функції опуклий догори, а при всіх 𝑥 > 1 і −  < 𝑥 < 1 графік функції опуклий донизу.

Приклад 2.4 Знайти проміжки монотонності та опуклості для функції

𝑒𝑥

𝑦 =  

𝑥

^′ = (𝑒𝑥^𝑥)^′ = (𝑒^𝑥)^′ ∙ 𝑥𝑥−₂ 𝑒^𝑥 ∙ 𝑥^′ = 𝑒^𝑥 ∙ 𝑥_𝑥−2 𝑒^𝑥 ∙ 1 = 𝑒^𝑥(𝑥_𝑥2− 1)

                      𝑦          

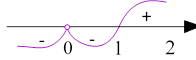
критичні точки І-го роду 𝑥 = 1 і 𝑥 = 0 – парної кратності; 𝑒^𝑥 > 0 при ∀𝑥 ∈ 𝑅, отже при 𝑥 = 2, 𝑓′(2) = 𝑒²(2−1) = 𝑒² > 0

                                                           4                 4

 х

 

При всіх 𝑥 < 0 і 0 < 𝑥 < 1 функція строго спадна, а при всіх 𝑥 > 1 – строго зростаюча.

^′′ = (𝑦^′)^′ = (𝑒^𝑥(𝑥𝑥₂− 1))^′ =

𝑦

((𝑒^𝑥)^′ ∙ (𝑥 − 1) + 𝑒^𝑥 ∙ (𝑥 − 1)^′) ∙ 𝑥² − 𝑒^𝑥 ∙ (𝑥 − 1) ∙ (𝑥²)^′

= 𝑥₄ =

          (𝑒^𝑥 ∙ (𝑥 − 1) + 𝑒^𝑥) ∙ 𝑥² − 𝑒^𝑥 ∙ (𝑥 − 1) ∙ 2𝑥          𝑒^𝑥 ∙ 𝑥((𝑥 − 1 + 1)𝑥 − 2(𝑥 − 1))

= 𝑥₄ =      _𝑥4                                                                                                         =

        𝑒^𝑥 ∙ (𝑥² − 2𝑥 + 2)         𝑒^𝑥 ∙ ((𝑥 − 1)² + 1)

= 𝑥3             =         _𝑥3          ;

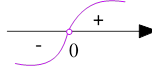
𝑒^𝑥 > 0 при ∀𝑥 ∈ 𝑅, вираз (𝑥 − 1)² + 1 > 0 при ∀𝑥 ∈ 𝑅, отже знак ІІ-ої похідної залежить тільки від знаменника.

 х

 

Очевидно, що при ∀𝑥 > 0, 𝑦^′′ > 0 , отже графік функції опуклий донизу, а при ∀𝑥 < 0, 𝑦^′′ < 0 – графік опуклий догори.

Для самоперевірки можна знайти інтервали монотонності та опуклості гра-

фіків функцій, вказаних до розділу 1.

 

3. Пошук областей розташування графіка функції

 

Інформація про область визначення функції, парність або непарність, точки перетину з координатними осями, інтервали знакосталості та асимптоти дозволяють вказати області, де будуть розташовані вітки графіка.

𝑥3

Приклад 3.1 𝑦 ⁼ 𝑥₂₋₄

𝐷(𝑦): 𝑥² − 4 ≠ 0 ⟺ 𝑥 ≠ ±2 або 𝑥 ∈ (−∞; −2) ∪ (−2; 2) ∪ (2; +∞).

𝐷(𝑦) – симетрична, знайдемо 𝑓(−𝑥):

𝑓 ⟹ 𝑓(−𝑥) = −𝑓(𝑥), отже, функція – непарна.

                          (−𝑥) −4                                       −4

При 𝑥  ⟹ графік функції проходить через початок координат т. О(0;0).

Знайдемо інтервали знакосталості функції: 𝑥 = 0 – корінь чисельника;   

33

𝑥 = ±2 – корені знаменника. При 𝑥 = 3, 𝑓(3) = 3₂₋₄ =  > 0.

 

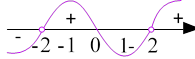х

 

 

При всіх 𝑥 < −2 і 0< 𝑥 < 2, 𝑦 < 0, а при всіх −2 < 𝑥 < 0 і 𝑥 > 2, 𝑦 > 0.

Знайдемо асимптоти: 𝑥 = ±2 – вертикальні асимптоти.

                                        𝑥³                                           𝑥           ±∞

⟹ горизонтальної асимптоти немає.

                      𝑥     ±∞ 𝑥_{2−𝑥         𝑥→                         1−0}

𝑥

                                              𝑓(𝑥)                           𝑥³                                               𝑥³                                          1               1

                       𝑘 = lim  𝑥 = lim 𝑥∙(𝑥2−4) = 𝑥lim→∞ 𝑥3−4𝑥 = 𝑥lim→∞ 1−𝑥42 = 1−0 = 1,       𝑘 = 1

                                  𝑥→∞                   𝑥→∞

                      Знайдемо b: 𝑥→∞     𝑥→∞                                                                                                               𝑥2−4 𝑥→∞ 𝑥2−4                          

                                           4𝑥                          4               4

= lim 𝑥2−4 = 𝑥lim→∞ 𝑥−4 = ∞−0 = 0. Отже, 𝑦 = 𝑥 – похила асимптота. 𝑥→∞

𝑥

 

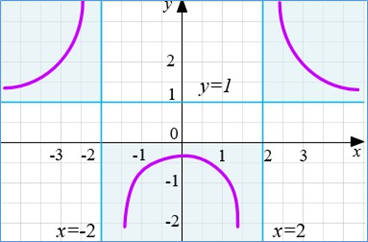
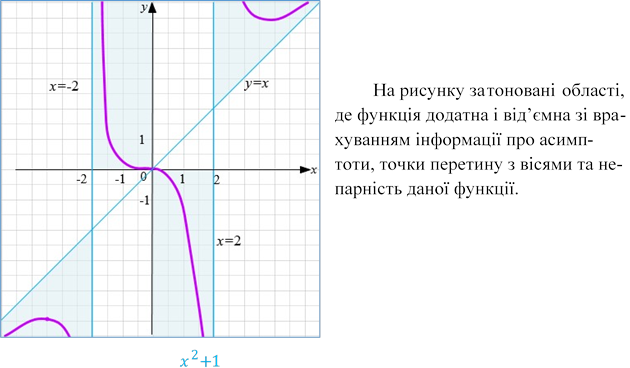Приклад 3.2 𝑦 (Дивись приклад 1.3)

𝐷(𝑦): 𝑥 = ±2 – симетрична, знайдемо 𝑓(−𝑥):

𝑓⟹ 𝑓(−𝑥) = 𝑓(𝑥), отже функція парна.

(−𝑥) −4

Так як 𝑥² + 1 > 0 при ∀𝑥 ∈ 𝑅, то 𝑦 ≠ 0, отже нема перетину з віссю (ОХ).

При 𝑥  ⟹  – точка перетину з віссю (ОУ)

Знайдемо інтервали знакосталості функції: 

при 𝑥 . Отже, при всіх 𝑥 ∈ (−2; 2), 𝑦 < 0, а на інтервалах (−∞; −2) і (2; +∞), 𝑦 > 0.

х

 

𝑥 = ±2 – вертикальні асимптоти. 𝑦 = 1 – горизонтальна асимптота

На рисунку також схематично показано графік функції.

 

 

 

 

𝑒𝑥

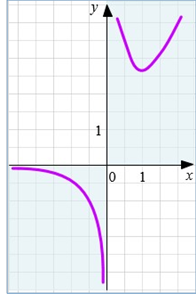
Приклад 3.3 𝑦 =  (Дивись приклад 2.4)

𝑥

𝐷(𝑦): 𝑥 ≠ 0

Функція загального типу ні парна, ні непарна. Перетину з вісями нема так

як 𝑥 ≠ 0 і 𝑒^𝑥 > 0 при ∀𝑥 ∈ 𝑅.

𝑒𝑥

Знак виразу  залежить тільки від знаменника, а саме при 𝑥 > 0,

𝑥 𝑒𝑥

𝑦 =  > 0, а при ∀𝑥 < 0, 𝑦 < 0. 𝑥 ≠ 0 – вертикальна асимптота, при цьому:

𝑥

                                    𝑒𝑥                                                                                   𝑒𝑥

lim  = +∞,    lim  = −∞. 𝑥→+0 𝑥            𝑥→−0 𝑥

Знайдемо горизонтальні асимптоти:

                        𝑥                                     ( 𝑥)′                                        𝑥                                                                             𝑥                                     ( 𝑥)′

                                                                                                         ,                                    ,

       𝑥→+∞ 𝑥           𝑥→+∞     𝑥^′                  𝑥→+∞ ¹                                    𝑥→−∞ 𝑥           𝑥→−∞     𝑥^′                  𝑥→−∞ 𝑒^𝑥

отже на проміжку (−∞; 0) горизонтальна асимптота існує, а саме 𝑦 = 0 (вісь (ОХ)), на проміжку від (0; +∞) горизонтальної асимптоти не існує.

З’ясуємо наявність похилої асимптоти, для цього знайдемо 𝑘:

𝑒𝑥

𝑥

                                       𝑘       𝑥→∞ 𝑥          𝑥→∞ 𝑥2         𝑥→∞ (𝑥2)′         𝑥→∞ 2𝑥       𝑥→∞ 2

Обчислимо окремо границю функції при 𝑥 → +∞ і при 𝑥 → −∞:

𝑒𝑥

𝑘₁ =    lim   ₂ = +∞, отже при 𝑥 → +∞ похилої асимптоти нема.

_𝑥→+∞

𝑥

𝑘₂ 𝑥→−∞ _{2 2 𝑥→−∞ 𝑒}𝑥 , а це говорить про те, що похила асимптота на інтервалі (−∞; 0) виродилася у горизонтальну 𝑦 = 0.

 

 

4. Загальна схема дослідження функцій і побудови їх графіків

 

При дослідженні функцій та побудові їхніх графіків можна використовувати таку схему:

1.       Знайти область визначення функції.

2.       Перевірити функцію на парність і непарність.

3.       Знайти координати точок перетину графіка функції з координатними осями.

4.       Знайти інтервали знакосталості функції.

5.       Знайти асимптоти графіка функції.

6.       Дослідити функцію на монотонність за допомогою першої похідної.

7.       Знайти точки екстремумів.

8.       Знайти інтервали опуклості та точки перегину.

9.       Знайти додаткові точки графіка функції, як правило, абсциси цих      точок є найближчими до критичних точок.

10.   Побудувати графік функції, враховуючи дослідження проведені в    пунктах 1-9.

 

Зауваження: в даних методичних рекомендаціях не розглядаються функції, для яких передбачено дослідження на періодичність. В зв’язку з цим із загальної схеми дослідження функції вилучено пункт про дослідження на періодичність.

 

5. Дослідження дробово-раціональних функцій та побудова їхніх 

графіків

𝑥²−4 𝑥−1

Приклад 5.1 𝑦 =  

1.        𝐷(𝑦): 𝑥 − 1 ≠ 0 ⟺ 𝑥 ≠ 1 або 𝑥 ∈ (−∞; 1) ∪ (1;+∞)

2.        𝐷(𝑦) – несиметрична, обчислимо 𝑓(−𝑥): 𝑥²−4

𝑓                                           ⟹ 𝑓(−𝑥) ≠ 𝑓(𝑥), 𝑓(−𝑥) ≠ −𝑓(𝑥), отже, функція загаль-

𝑥+1

ного типу, ні парна, ні непарна.

3.        При 𝑥 = 0: 𝑓(0) =  = 4 ⟹ (0; 4) – точка перетину графіка функції з віссю (ОУ).

4.        Знайдемо інтервали знакосталості функції 𝑥 = ±2 – корені чисельника,

𝑥 = 1 – корінь знаменника. При 𝑥 . Отже, при всіх 𝑥 < −2 і 1 < 𝑥 < 2, 𝑦 < 0, а при ∀𝑥 > 2, −2 < 𝑥 < 1, 𝑦 > 0.

х

 

 

5.        Знайдемо асимптоти графіка функції:

𝑥 = 1 – вертикальна асимптота (𝑥 − 1 = 0 ⟺ 𝑥 = 1).  ²−4 

∞ ⟹ горизонтальної асимптоти немає.

𝑥→∞ 𝑥−1            𝑥→

𝑥

Шукаємо похилу асимптоту:

                       𝑓(𝑥)                  𝑥² − 4                 𝑥² − 4

𝑘 = lim  = lim  = lim  = lim                      =              = 1;𝑘 = 1

            𝑥→∞      𝑥         

𝑥² − 4 𝑥² − 4 − 𝑥² + 𝑥 𝑥 − 4

𝑏 = lim (𝑓(𝑥) − 𝑘𝑥) = lim (− 𝑥) = lim  = lim  =

            𝑥→∞                                        𝑥→∞       𝑥 − 1                  𝑥→∞                𝑥 − 1                𝑥→∞ 𝑥 − 1

. Отже, 𝑦 = 𝑥 + 1 – похила асимптота

        𝑥→∞ 1−       1−0

𝑥

6. Дослідимо функцію на монотонність. Для цього знайдемо першу   по-

хідну функції

 

^′ = (𝑥𝑥²−−14)^′ = (𝑥² − 4)^′ ∙ (𝑥 −(1𝑥)−−1()𝑥₂² − 4) ∙ (𝑥 − 1)^′ =

𝑦

       2𝑥 ∙ (𝑥 − 1) − (𝑥² − 4) ∙ 1        2𝑥² − 2𝑥 − 𝑥² + 4        𝑥² − 2𝑥 + 4       (𝑥 − 1)² + 3

⁼                   (𝑥 − 1)^{2                         =}            (𝑥 − 1)^{2               =}     (𝑥 − 1)^{2       =}      (𝑥 − 1)²     

 

Знайдемо критичні точки І-го роду, по-перше це точки, в яких похідна не існує, тобто 𝑥 = 1. По-друге, це точки, в яких 𝑦^′ = 0, але таких точок не існує, так як (𝑥 − 1)² + 3 > 0 при всіх 𝑥 ∈ 𝑅.

Отже, знак похідної залежить від знаку знаменника, який завжди більший нуля. Це говорить про те, що при всіх 𝑥 ≠ 1,  𝑦^′ > 0, тобто при ∀𝑥 ≠ 1 функція є строго зростаючою.

 х

                                                                                            0        1

 

 

7.                Точок екстремума немає, так як 𝑥 = 1 не входить в область визначення функції і похідна при переході через точку 𝑥 = 1 не міняє знак.

8.                Дослідимо функцію на опуклість та точки перегину. Для цього знай-

демо похідну ІІ-го порядку:

𝑥2 − 2𝑥 + 4 ′

𝑦′′ = (𝑦′)′ = ( (𝑥 − 1)2        ) =  

(𝑥² − 2𝑥 + 4)^′ ∙ (𝑥 − 1)² − (𝑥² − 2𝑥 + 4)((𝑥 − 1)²)^′

 

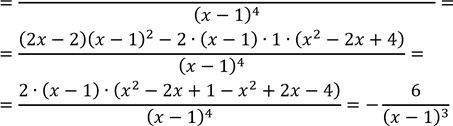
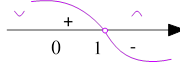
𝑦^′′ ≠ 0,   𝑥 = 1 – критична точка ІІ-го роду.

Очевидно, що при 𝑥 > 1, 𝑦^′′ < 0, 𝑥 < 1, 𝑦^′′ > 0.

При всіх 𝑥 ∈ (−∞; 1) графік функції опуклий донизу, а при всіх 𝑥 > 1 графік опуклий догори. Точки перегину нема, так як 𝑥 = 1 ∉ 𝐷(𝑦).

 х

 

9.                Знайдемо додаткові точки:

 

𝑥 = −4,                              16 − 4       12                                               (−4; −2,4)

                                            𝑓(−4) = = = −2,4

                                                                     −4 − 1      −5

𝑥 = −3,                               9 − 4            5                                              (−3; −1,25)

                                            𝑓(−3) =                 = −  = −1,25

4

1                    0,25 − 4        −3,75           375    (0,5; 7,5)

𝑥 =      ,                𝑓 ( ) = =   = = 7,5

2                    0,5 − 1           −0,5  50

𝑥 = 3,	9 − 4      5 𝑓(3) =              =     = 2,5                      3 − 1      2	(3; 2,5)
𝑥 = 4,	16 − 4      12 𝑓(4) = = = 4                       4 − 1         3	(4; 4)

 

10.           Враховуючи дослідження проведені в пунктах 1-9, побудуємо графік функції:

 

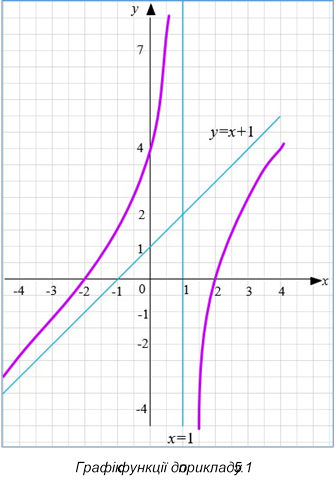
Завдання для самоперевірки:

𝑥

1. 𝑦 ⁼ 1+𝑥₂

4+𝑥

2. 𝑦 ⁼ 𝑥₂

𝑥

3.     𝑦 = 𝑥2−1

𝑥3

4.     𝑦 = 𝑥2+2𝑥+3 𝑥+2

5. 𝑦 ⁼ 𝑥₃

𝑥3

6. 𝑦 ⁼ 2(𝑥+1)₂ 6−𝑥³

                                                                                                                                                   7. 𝑦 ⁼ 𝑥₂

 

6. Дослідження трансцендентних функцій та побудова їхніх графіків

 

Приклад 6.1 Дослідити функцію 𝑦 = 𝑥 ∙ 𝑒^−𝑥 та побудувати її графік.

1.        𝐷(𝑦): 𝑥 ∈ 𝑅, так як 𝑒^−𝑥 > 0 при ∀𝑥 ∈ 𝑅.

2.        𝑓(−𝑥) = −𝑥 ∙ 𝑒^𝑥;  𝑓(−𝑥) ≠ 𝑓(𝑥) і 𝑓(−𝑥) ≠ −𝑓(𝑥), отже, функція загального типу, ні парна, ні непарна.

3.        При 𝑥 = 0 𝑓(0) = 0 ∙ 𝑒⁰ = 0 ∙ 1 = 0 ⟹ графік функції проходить через початок координат (0;0).

4.        Знак функції залежить від знака х, а саме: при 𝑥 > 0, 𝑦 > 0, а при 𝑥 < 0,𝑦 < 0. 5. Вертикальної асимптоти немає, так як 𝑥 ∈ 𝑅.

Визначимося щодо вертикальної асимптоти, обчислимо:

−𝑥 = lim 𝑒𝑥𝑥 = 𝑥lim→+∞ 𝑒1𝑥 = 0 lim 𝑓(𝑥) = lim 𝑥 ∙ 𝑒

𝑥→+∞                     𝑥→+∞                           𝑥→+∞

                          −𝑥             ∞.

𝑥

Отже, при 𝑥 → +∞ функція має горизонтальну асимптоту 𝑦 = 0 (сама вісь (ОХ)), при 𝑥 → −∞,𝑦 → −∞. Похилої асимптоти немає, так як 𝑘 = 0, а саме:

                       𝑓(𝑥)                𝑥 ∙ 𝑒^−𝑥                      1

𝑘 = lim  𝑥 = lim→∞ 𝑥 = lim 𝑥 = 0

            𝑥→∞                      𝑥                                   𝑥→∞ 𝑒

6.        Знайдемо інтервали монотонності:

𝑦^′ = (𝑥 ∙ 𝑒^−𝑥)^′ = 𝑥^′ ∙ 𝑒^−𝑥 + 𝑥 ∙ (𝑒^−𝑥)^′ = 1 ∙ 𝑒^−𝑥 + 𝑥 ∙ 𝑒^−𝑥 ∙ (−1) = 𝑒^−𝑥 ∙ (1 − 𝑥) 𝑦^′ = 0 ⟹ 1 − 𝑥 = 0 ⟺ 𝑥 = 1 – критична точка І-го роду.

Знак похідної залежить від знака виразу (1 − 𝑥), так як 𝑒^−𝑥 > 0 при всіх 𝑥 ∈ 𝑅. При 𝑥 > 1, 𝑦^′ < 0 ⟹ при 𝑥 ∈ (1; +∞) – функція строго спадна. При 𝑥 < 1,𝑦^′ > 0 ⟹ при 𝑥 ∈ (−∞; 1) – функція є строго зростаючою.

 

х

                                                                                     0       1

 

7.        𝑥 = 1 – точка максимуму. 𝑓. Отже, ма-

𝑒

ємо точку графіка (1; ¹).

𝑒

8.        Проведемо дослідження функції на опуклість та точку перегину:

𝑦^′′ = (𝑒^−𝑥 ∙ (1 − 𝑥))^′ = (𝑒^−𝑥)^′ ∙ (1 − 𝑥) + 𝑒^−𝑥 ∙ (1 − 𝑥)^′ = −𝑒^−𝑥 ∙ (1 − 𝑥) +

+𝑒^−𝑥 ∙ (−1) = −𝑒^−𝑥 ∙ (1 − 𝑥 + 1) = −𝑒^−𝑥 ∙ (2 − 𝑥) = 𝑒^−𝑥(𝑥 − 2) ⟹ 𝑥 = 2 – критична точка ІІ-го роду. Знак другої похідної залежить від знака виразу (𝑥 − 2).

При 𝑥 > 2, 𝑦^′′ > 0 ⟹ графік функції опуклий донизу. х При 𝑥 < 2, 𝑦^′′ < 0 ⟹ графік функції опуклий догори.

0 1 2                          𝑥 = 2 – абсциса точки перегину.

                                                                  𝑓 𝑒 , отже, (2; 𝑒²₂) – точка перегину.

9.        Обчислимо значення функції у додаткових точках:

 

                     𝑥 = −1,             𝑓(−1) = −1 ∙ 𝑒¹ = −𝑒 ≈ −2,7               (−1; −2,7)

(0,5; 0,3)

                       𝑥 =,                 𝑓

𝑥 = 1,5,	𝑓(1,5) = 1,5 ∙ 𝑒−1,5 ≈ 0,33	(1,5; 0,33)
𝑥 = 2,5,	𝑓(2,5) = 2,5 ∙ 𝑒−2,5 ≈ 0,21	(2,5; 0,21)
𝑥 = 3,	𝑓(3) = 3 ∙ 𝑒−3 ≈ 0,15	(3; 0,15)

10.    Побудуємо графік функції:

 

 

 

 

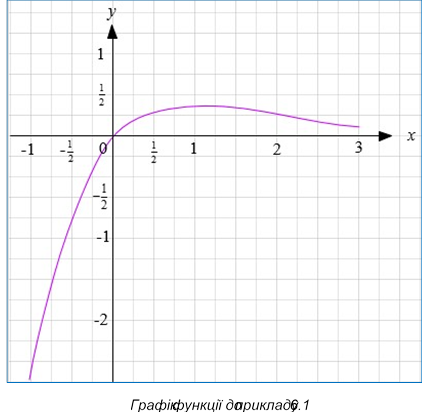
Завдання для самоперевірки:

 

1.                   y = 𝑥 ∙ 𝑒^𝑥

2.                   y = 𝑥 ∙ ln 𝑥

3.                   y = ln²𝑥

4.                   y = ln|cos 𝑥|

1+𝑥

5.                   y = ln ||

1−𝑥

6.                   𝑦 = sin 𝑥 + 𝑥

7.                   𝑦 = cos 𝑥 − 𝑥

8.                   𝑦 = 𝑥 + 𝑒^−𝑥

9.                   𝑦 = ln(𝑥² + 1)

10.       y = 𝑒^−𝑥2

7. Завдання для практичної роботи  «Побудова графіків дробово-раціональної функції»

 

 

𝑥²−1 𝑥−2

1. y =  

𝑥²+1

                              2.        y =  

2𝑥+3

𝑥²−𝑥+6

                              3.           y =  

𝑥−2

𝑥−2

                              4.      y ⁼ 𝑥₂

𝑥3

5.                   y = 𝑥₂₋₉

2𝑥+1

6.                   y = 𝑥2−1

𝑥3

7.                   y = 𝑥2−1

5(𝑥−2)

8.                   y ⁼   𝑥₂

𝑥3

                              9.        y =  

𝑥−1

𝑥2

                              10.      y =  

𝑥−3

𝑥3

11.              y = 𝑥2−4

6−𝑥³

12.              y ⁼   𝑥₂

𝑥²+9𝑥+9

                              13.       y =  

𝑥

𝑥

                              14. y = 𝑥2−4

𝑥²+1

                              15.      y =  

2𝑥+3

 

𝑥

        16. y ⁼ 1+𝑥₂

𝑥2−1

        17.    y ⁼ 𝑥₄

2

        18. y = 𝑥2−4

3𝑥²+1

        19.        y =  

𝑥

(𝑥−1)²

        20.       y =  

𝑥+2

𝑥

21.              y = 𝑥2+1

𝑥²−1

22.              y = 𝑥2−9

𝑥³+𝑥

23.              y = 𝑥2−1

𝑥²−3

        24.          y =  

𝑥

𝑥²+8

        25.          y =  

𝑥+1

𝑥3

26.              y = 3𝑥2−1

𝑥−1

27.              y ⁼ 𝑥₃

𝑥2

        28.      y =  

𝑥+3

𝑥²−4

        29. y = 𝑥2+1

𝑥3

        30.      y =  

𝑥+2

 

 

 

 

21

 

 

Літературні джерела

 

1.     П.П. Овчинников, Ф.П Яремчук, В.М. Михайленко. Вища математика,

ч. І. – К.: «Техніка», 2000, 590 с.

2.     Н.С. Пискунов. Дифференциальное и интегральное исчисление. – М. «Интеграл-пресс», 2009, 415 с.

3.     Л.І. Дюженкова, О.Ю. Дюженкова, Г.О. Михалін. Вища метематика.

Приклади і задачі. – К.: Академія, 2002, 622 с.

 

22