Методичні рекомендації "Побудова графіків складених функцій на основі поняття монотонності"
Проаналізувавши деякі вправи ЗНО, можна помітити, що досить значна увага приділяється побудові графіків функцій та графічному розв'язанню ряду завдань. Вміння будувати графіки функцій і їх читати, тобто визначати проміжки монотонності, екстремальні значення та інші характеристики функції по її графіку, – важливий елемент математичної культури.
У багатьох задачах побудова графіка є лише допоміжним елементом розв'язування. Тому з'являється необхідність познайомити учнів з різними прийомами побудови графіків. На тестуванні не завжди час працює на учня, а тому він повинен твердо знати, як впоратись із завданням, витративши на нього мінімум часу. На тестуванні не завжди час працює на учня, а тому він повинен твердо знати, як впоратись із завданням, витративши на нього мінімум часу.
У роботі наведена схема побудови графіків складених функцій елементарними способами без застосування похідної.
ПОБУДОВА ГРАФІКІВ СКЛАДЕНИХ ФУНКЦІЙ НА ОСНОВІ ПОНЯТТЯ МОНОТОННОСТІ
Проаналізувавши деякі вправи ЗНО, можна помітити, що досить значна увага приділяється побудові графіків функцій та графічному розв’язанню ряду завдань.
Вміння будувати графіки функцій і їх читати, тобто визначати проміжки монотонності, екстремальні значення та інші характеристики функції по її графіку, – важливий елемент математичної культури. Ці вміння необхідні майбутньому техніку, економісту, інженеру, лікарю. У багатьох задачах побудова графіка є лише допоміжним елементом розв’язування. Тому з’являється необхідність познайомити учнів з різними прийомами побудови графіків.
На тестуванні не завжди час працює на учня, а тому він повинен твердо знати, як впоратись із завданням, витративши на нього мінімум часу. Звичайно, в програмі є питання побудови графіків функцій із застосуванням похідної, але там обчислювальна, формальна сторона переважає над логічною та графічною.
Побудову графіка складеної функції ![]() в деяких випадках можна здійснити за такою схемою:
в деяких випадках можна здійснити за такою схемою:
-
Накреслити графіки внутрішньої
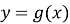 і зовнішньої
і зовнішньої 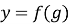 функцій та систему координат
функцій та систему координат 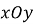
-
Визначити проміжки монотонності внутрішньої функції
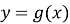 і відмітити їх на осі
і відмітити їх на осі 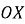
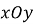
-
На кожному проміжку визначити границі зміни функції
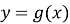 і вибрати ті значення
і вибрати ті значення 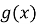 , які попадають в область визначення функції
, які попадають в область визначення функції 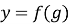 .
.
-
По графіку зовнішньої функції
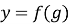 знайти характер її зміни.
знайти характер її зміни.
-
В системі координат
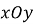
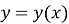
Працюючи за цією схемою, учні постійно звертаються до графіків основних елементарних функцій, вчаться по графіку слідкувати за зміною функції при зміні аргумента і навпаки по заданій зміні функції будувати її графік. При цьому графік сприймається не як статичний образ, а як відображення руху. Цей рух слід постійно підкреслювати, показуючи учням саме зростання чи спадання змінної величини.
Навчившись елементарними способами будувати графіки складених функцій, учні отримають великий запас ілюстрацій властивості неперервності, різних видів розривів, односторонніх границь. Володіючи цією методикою, найбільш підготовлені учні, тільки дивлячись на формулу, що задає функцію, відразу малюють ескіз її графіка.
Використовуючи схему побудови графіка функції ![]() , учні оволодівають також вмінням представляти складену функцію у вигляді композиції двох функцій – внутрішньої та зовнішньої, навичками «бачити» ці дві функції, без чого неможливо обійтися при вивченні диференціювання складених функцій.
, учні оволодівають також вмінням представляти складену функцію у вигляді композиції двох функцій – внутрішньої та зовнішньої, навичками «бачити» ці дві функції, без чого неможливо обійтися при вивченні диференціювання складених функцій.
Розглянемо деякі приклади.
-
Побудувати графік функції
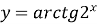 .
.
Дана функція є композицією двох функцій: зовнішньої ![]()
![]() . Внутрішня функція є строго зростаючою: при зростанні
. Внутрішня функція є строго зростаючою: при зростанні ![]()
![]()
![]()
![]() зростає від 0 до
зростає від 0 до ![]()
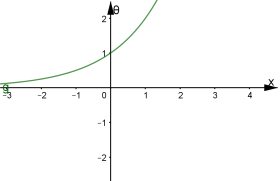
![]() По графіку зовнішньої функції визначаємо, що при такій зміні
По графіку зовнішньої функції визначаємо, що при такій зміні![]() відповідає зростання функції
відповідає зростання функції ![]()
![]() . Отже, при зростанні
. Отже, при зростанні ![]()
![]()
![]()
![]() . Контрольна точка (0;
. Контрольна точка (0;![]() )
)
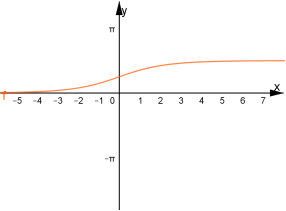
![]()
-
Побудувати графік функції
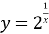 .
.
Будуємо графіки внутрішньої ![]() і зовнішньої
і зовнішньої ![]() функцій.
функцій.
![]()
![]()
Визначаємо проміжки монотонності внутрішньої функції: (![]()
![]()
![]()
![]()
![]() спадає від 0 до
спадає від 0 до ![]()
![]()
![]() від 1 до 0. Якщо ж
від 1 до 0. Якщо ж ![]()
![]()
![]()
![]()
![]() спадає від
спадає від ![]()
![]() спадає від
спадає від ![]()
Контрольні точки: ![]()
![]()
-
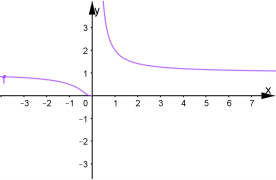
Побудувати графік функції
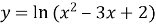 .
.
Зобразимо графіки внутрішньої ![]() та зовнішньої
та зовнішньої ![]() функцій.
функцій.
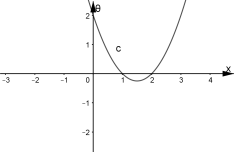
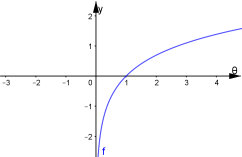
![]()
Якщо від![]()
![]()
![]() спадає від +
спадає від +![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() не визначена. Якщо ж
не визначена. Якщо ж ![]()
![]()
![]() зростає від 0 до +
зростає від 0 до +![]()
![]() при цьому зростає від
при цьому зростає від ![]()
![]()
-
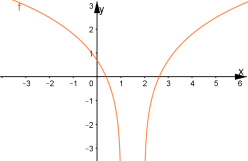
Побудувати графік функції
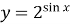 .
.
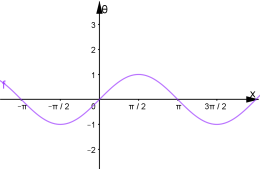
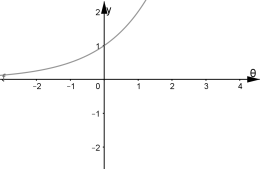
Зобразимо графіки внутрішньої ![]() та зовнішньої
та зовнішньої ![]() функцій.
функцій.
![]()
![]()
При зростанні ![]()
![]()
![]() зростає від 0 до 1, а
зростає від 0 до 1, а ![]()
![]()
![]() до
до ![]()
![]() спадає від 1 до 0, а
спадає від 1 до 0, а ![]()
![]()
![]()
![]()
![]() спадає від 0 до –1, а
спадає від 0 до –1, а ![]()
![]()
![]() до
до ![]()
![]() зростає від –1 до 0, а
зростає від –1 до 0, а ![]()
Функція є періодичною, тому досить побудувати графік на відрізку, довжина якого дорівнює періоду функції.
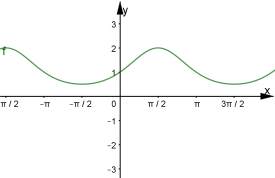
![]()
5. Побудувати графік функції ![]() .
.
В цьому завданні ![]() . Побудуємо графіки вказаних функцій.
. Побудуємо графіки вказаних функцій.
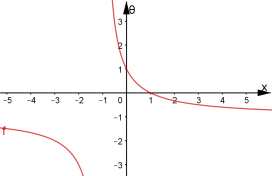
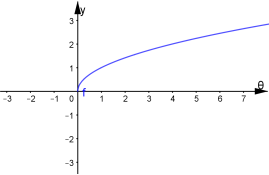
![]()
Якщо ![]() , тобто функція
, тобто функція ![]() не визначена при цих значеннях
не визначена при цих значеннях ![]()
![]() , то
, то ![]() спадає від
спадає від ![]()
![]()
![]()
![]()
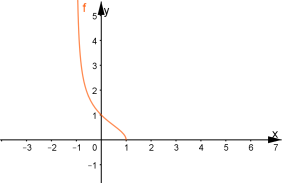
![]()
-
Побудувати графік функції
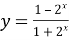 .
.
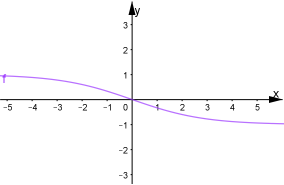
В даному випадку ![]() . Якщо
. Якщо ![]()
![]()
![]()
![]() зростає від 0 до +
зростає від 0 до +![]()
![]()
![]()
![]()
-
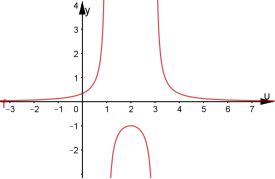
Побудувати графік функції
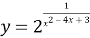 .
.
Дана функція є композицією трьох функцій ![]()
![]()
![]() .
.
![]()
![]()
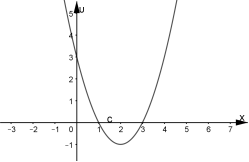
Без додаткових пояснень легко побудувати графік функції ![]() . Якщо
. Якщо ![]()
![]()
![]() зростає від 0 до +
зростає від 0 до +![]()
![]() зростає від 1 до +
зростає від 1 до +![]()
![]()
![]()
![]() спадає від
спадає від ![]()
![]() спадає від
спадає від ![]()
![]()
![]()
![]() зростає від
зростає від ![]()
![]()
![]()
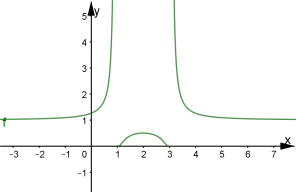
![]() спадає від –1 до
спадає від –1 до ![]()
![]()
![]()
-
Побудувати графік функції
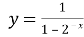 .
.
Дана функція є композицією трьох функцій ![]() .
.
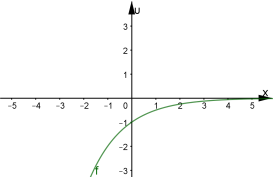
Побудуємо графіки перших двох функцій.
Очевидно ![]()
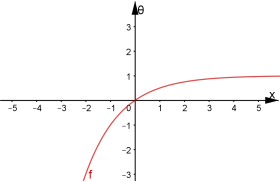
![]()
Якщо ![]()
![]()
![]() зростає від
зростає від ![]()
![]() спадає від 0 до
спадає від 0 до ![]()
![]()
![]()
![]() зростає від 0 до 1, а
зростає від 0 до 1, а ![]() спадає від
спадає від ![]()
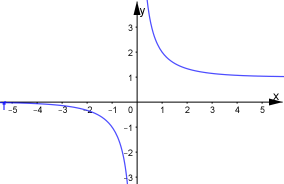
![]()
-
Побудувати графік функції
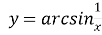 .
.
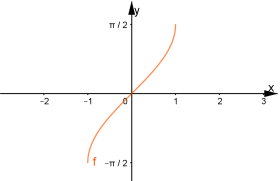
Дану функцію можна представити як композицію двох функцій ![]() ,
,
![]() . Функція
. Функція ![]()
![]() . Тобто
. Тобто ![]()
![]()
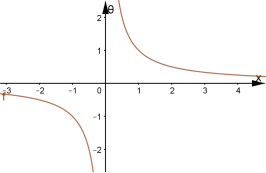
![]()
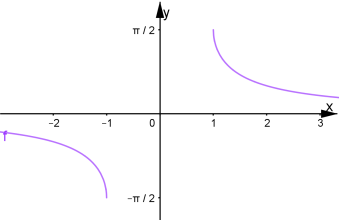
Якщо ![]()
![]()
![]()
![]() спадає від 0 до
спадає від 0 до ![]()
![]()
![]()
![]() . Якщо
. Якщо ![]()
![]()
![]() спадає від 1 до 0, а
спадає від 1 до 0, а ![]()
![]() до 0.
до 0.
![]()
-
Побудувати графік функції
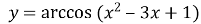 .
.
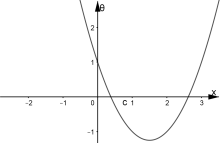
Дану функцію можна представити як композицію двох функцій
![]() ;
; ![]()
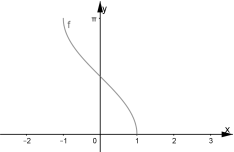
![]()
![]()
Функція ![]()
![]() . Тобто
. Тобто ![]() .
.
Звідси 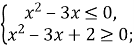
![]()
Отже, ![]() .
.
При зростанні ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
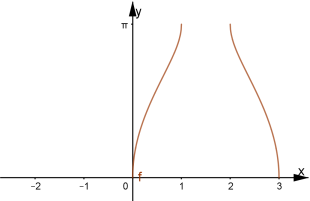
Побудувати графік функції
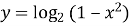
В даному випадку ![]() .
.
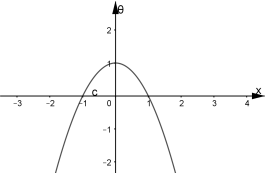
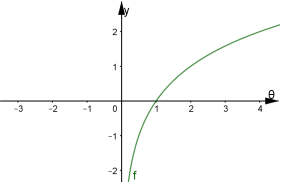
![]()
Побудуємо графік параболи![]() . На інтервалах
. На інтервалах ![]() та
та![]() графік
графік ![]() знаходиться під віссю ОХ, а, отже, там не існує графіка
знаходиться під віссю ОХ, а, отже, там не існує графіка![]() . В точках перетину графіка параболи з віссю віссю ОХ (0;1) та (0;
. В точках перетину графіка параболи з віссю віссю ОХ (0;1) та (0;![]()
![]() .
.
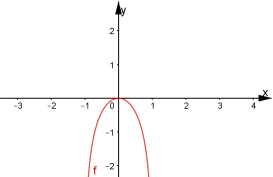
![]()
-
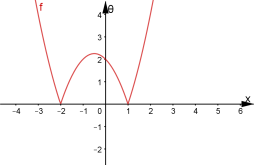
Побудувати графік функції
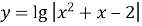 .
.
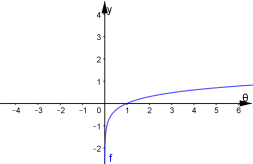
Дану функцію можна представити як композицію двох функцій
![]() ,
, ![]()
![]()
![]()
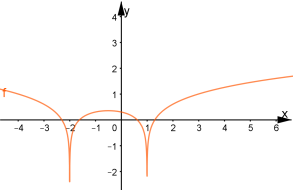
Знайдемо точки перетину графіка ![]() з прямою у=1. Абсциси цих точок – це точки перетину майбутнього графіка логарифмічної функції з віссю ОХ . Їх чотири. Прямі
з прямою у=1. Абсциси цих точок – це точки перетину майбутнього графіка логарифмічної функції з віссю ОХ . Їх чотири. Прямі ![]()
![]()
![]()
![]()
![]()
![]() спадає від
спадає від ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() зростає від 0 до 2,25, а
зростає від 0 до 2,25, а ![]()
![]()
![]()
![]()
![]()
![]() спадає від
спадає від ![]()
![]()
![]()
![]()
![]() зростає від 0 до
зростає від 0 до ![]()
![]()
![]()
![]()
![]()
![]()
Вправи для самостійної роботи
Побудувати графік функції:
-
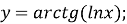
-
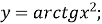
-
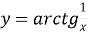 ;
;
-
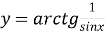 ;
;
-
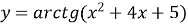 ;
;
-
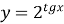 ;
;
-
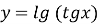
-
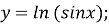
-
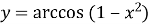 ;
;
-
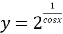 .
.


про публікацію авторської розробки
Додати розробку
