Методичні рекомендації "Розвиток математичної грамотності на уроках хімії. Розв’язування задач на розчини, суміші та сплави нестандартними способами."

Розвиток математичної грамотності на уроках хімії.

Розв’язування задач на розчини, суміші та сплави нестандартними способами.

  Зміни в характері освіти для кінця XX - початку XXI століття полягають в його спрямованості, цілях, змісті, які все більш явно орієнтують його на «вільний розвиток людини», на творчу ініціативу, самостійність учнів, конкурентоспроможність, мобільність майбутніх фахівців. 
У зв’язку з цим все більш актуальним стає компетентнісний підхід у освіті, формування ключових компетенцій людини є перспективним напрямком в науці і практиці освіти.  Однією з десяти компетенцій, якими повинен володіти випускник нової української школи є математична грамотність. Це - уміння застосовувати математичні (числові та геометричні) методи для вирішення прикладних завдань у різних сферах діяльності, здатність до розуміння і використання простих математичних моделей, уміння будувати такі моделі для вирішення проблем. Багато років тому славнозвісний математик Піфагор говорив своїм учням: «Ніколи не роби того, чого не знаєш, але навчись усьому, що треба знати». 

Розв’язування розрахункових задач з хімії – одна зі складових хімічної освіти поряд із вивченням і засвоєнням теоретичного матеріалу та опануванням технікою експерименту. Систематичне розв’язування задач сприяє формуванню глибоких і міцних знань, свідомих і стійких умінь, розвитку логічного мислення учнів.

Актуальною проблемою сьогодні є методики ефективного засвоєння різноманітної інформації. Постійне збільшення обсягу інформації у поєднанні з високою конкуренцією та вимогами суспільства, із одного боку, приводить до інтенсифікації освітнього процесу, а з другого – до цілої низки порушень психічного здоров’я школярів. Проте одним із завдань сучасної освіти є не лише надання високого рівня знань, а й збереження здоров’я  дитини.

 Думаю, треба пам’ятати  деякі основні поняття без яких неможливе  якісне навчання та засвоєння інформації. По-перше, одним із важливих наукових досягнень виявилось відкриття про спеціалізацію півкуль головного мозку. Вчені з’ясували, що права півкуля сприймає та обробляє інформацію з довкілля цілісно, а ліва – послідовно. Праву півкулю умовно називають «Художником», тому що вона найбільш активна при творчій діяльності, сприйнятті ритму, рими, інтонацій, просторовій орієнтації, розпізнаванні емоцій, запам’ятовуванні образів, у тому числі й людських обличь. Ліву півкулю умовно називають «Мислителем» і вона найбільш активна під час процесів логічного і абстрактного мислення, обчисленнях, вивченні мов (мова – це послідовність речень, які складаються з послідовності слів, які в свою чергу складаються з послідовності звуків).

Врахування функціональної асиметрії мозку – один із важливих факторів в організації навчання учнів   з переважанням правопівкулевого мислення, оскільки шкільні програми та підручники здебільшого розраховані на навчання школярів з домінуючою лівою півкулею. На жаль, в школі, починаючи з першого класу, прийнято смиренно сидіти, не рухатись, букви і числа вчити лінійно, читати і писати на дошці чи в зошиті, тобто лівопівкулевим способом. Таке навчання швидко перетворюється на дресирування дитини, приводить до зниження мотивації, стресів і неврозів. Зловживання термінами і абстрактними поняттями знижує пізнавальний інтерес дитини, формує звичку до зубріння.

По-друге, сприйняття нової інформації  та її запам’ятовування відбувається в трьох напрямках і, в залежності від активності аналізаторів, учнів можна розділити на три групи – «слухачі», «глядачі», «діячі». Пояснюючи нові поняття, терміни, типи задач обов’язково необхідно враховувати ці фактори і відкрити дітям нові можливості для сприйняття інформації. По-третє, нові стандарти освіти націлюють вчителів на розвиток у дітей різноманітних компетенцій, які адаптують їх до дорослого життя. Сучасні вимоги європейського рівня розвитку освіти сприяють вільному вибору засобів навчання та максимальній самореалізації в умовах психологічного комфорту.  Одним із важливих принципів сучасної освіти є оптимізація навчання через застосування новітніх освітніх психолого-педагогічних технологій.

Одне з першочергових завдань школи – забезпечення якості і міцності знань і умінь, розвиток розумових здібностей учнів. Використання задач у навчальному процесі допомагає реалізовувати це завдання.

  Хочу поділитися   інформацією про використання мнемотехнічних методів і прийомів  як  ефективного компетентнісного підходу для навчання  в умовах сучасної освіти. Мнемотехніка (від грецької – пам’ять і мистецтво) – це спосіб покращення нової інформації шляхом утворення асоціативних зв’язків за допомогою спеціальних методів і прийомів. Основними мнемічними процесами є: збереження, забування, відтворення і впізнавання. Відомо, що пам’ять – найбільш тренований пізнавальний процес. Головна умова розвитку пам’яті – вправи і тренування. Адже саме на пам’ять у процесі навчання припадає особливе навантаження.   Рівень розвитку мнемічних процесів   впливає на успішність навчання школярів. Мнемотехніка належить до здоров’язбережувальної технології, що забезпечує оптимізацію розумової діяльності в умовах сучасної освіти.  

Пропоную розглянути це на конкретному прикладі – під час вивчення теми «Розчини. Масова частка розчиненої речовини». Ці задачі характеризуються великою варіантністю, обсягом і складністю. Побачивши задачу на суміші, розчини чи сплави, учні не завжди поспішають її розв’язувати, вважаючи їх дуже важкими. Я пропоную розглянути   різні способи та методи розв’язування задач,  застосовуючи мнемотехніки, що дозволяє безпомилково запам’ятовувати будь-яку точну інформацію, яка вважається важкою для запам’ятовування, а також сприяє  підготовці учня до діяльності в умовах сучасного інформаційного суспільства.

  Починаю ознайомлення з задачами даного типу із розв’язування задач на обчислення масової частки розчиненої речовини.

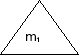  Похідні формули на визначення маси розчиненої речовини та маси розчину      можна записати в готовому вигляді і запропонувати для запам’ятовування. Але використання готових похідних формул не сприяє розвитку розумових здібностей учнів. Тому варто вдосконалювати математичні знання учнів, пропонуючи самим знайти ділене чи дільник.

m₁ – маса речовини;

m₂ – маса розчину;

 w – масова частка розчиненої речовини

Прямі й обернені задачі дають змогу дослідити здатність до зворотнього процесу мислення. Щоб виконати таке завдання, учень повинен не тільки змінити хід думки з прямого на зворотній, а й виконати цілу систему мислительних операцій.

Далі ускладню і пропоную учням задачу на обчислення масової частки розчиненої речовини у розчині під час його розведення і задачу на обчислення масової частки розчиненої речовини у розчині при збільшенні розчиненої речовини.

Наступна задача дещо вища за рівнем складності: обчислення масової частки речовини в розчині, що утворився з двох вихідних розчинів з відомими масами і масовими частками речовини в них.

Пропоную учням уявити собі, що вони приготували два розчини. Один з них надто солодкий, а другий - замало солодкий. При їх змішуванні виявилось, що саме такої концентрації розчин   підходить. Як дізнатися, якої концентрації цей розчин?

  Цю ж саму задачу можна представити дітям у вигляді малюнка з основними даними задачі та їх взаємодіями. Використовуючи   пропорції приходимо до того ж результату. 

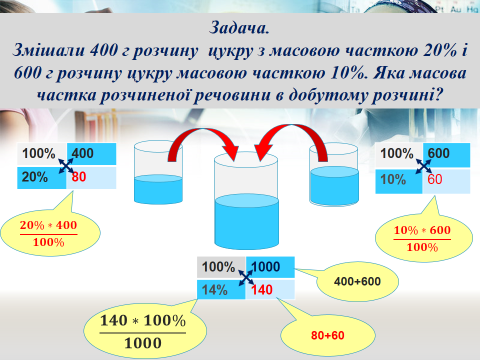
 Але при такому розв’язуванні працюють зорові рецептори, які збільшують обсяг інформації для мозку та  залучають  до роботи  інші центри. Інформація, отримана таким чином матиме більший діапазон та глибше сприйняття.

Розглянемо наступні задачі.

1.               Є два сплави міді зі свинцем (різновид бронзи). Один сплав містить 15% міді, а інший – 65%. Скільки треба взяти кожного сплаву, щоб отримати 200 грамів сплаву, який містить 30% міді?
2.               Скільки грамів 4% і 10% розчинів солі треба взяти, щоб отримати 180 грамів 6% розчину?
3.               В першому бідоні було молоко, масова частка жиру в якому становила 3%, а в другому – вершки, жирністю 18%. Скільки треба взяти молока і скільки вершків, щоб отримати 10літрів молока з масовою часткою жиру 6%.

Задачі подібні за змістом, хоча одна на сплави, друга на розчини, а третя на суміші, а значить і розв’язуватися будуть за одним алгоритмом.

Я пропоную учням раціональні, нестандартні способами розв’язування задач на суміші, розчини та сплави.

       1. Розв’язування задач «Методом чаш».

Суть методу  полягає в наступному: необхідно зобразити кожен сплав (розчин, суміш) у вигляді прямокутника, розбитого на фрагменти. Після заповнюємо отримані прямокутники відповідно до умови задачі:

1) Над кожним «маленьким» прямокутником вказуємо відповідні компоненти сплаву (суміші, розчину)

2) Всередині прямокутників вписуємо процентний вміст відповідного компонента. Якщо сплав (суміш, розчин) складається з двох компонентів, то досить вказати процентний вміст одного з них. В цьому випадку процентний вміст другого компонента дорівнює різниці 100% і процентного вмісту першого.

3) Під прямокутником записуємо масу (або  об’єм) відповідного сплаву (або компонента). І враховуючи, що маса сплаву (розчину, суміші) кількох речовин дорівнює сумі мас компонентів, складаємо рівняння.

         2. Табличний спосіб.   При розгляді задач даного змісту, зручно використовувати таблицю, оскільки зорове сприйняття розміщених величин в таблиці дає додаткову інформацію, яка полегшує процес розв’язування задачі та її перевірки. 

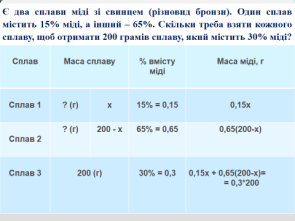
    3. «Правило хреста» або «Конверт Пірсона».

Даний спосіб запропонував англійський математик, статистик, біолог і філософ Карл Пірсон.

Це зручний і раціональний спосіб  розв’язування задач. Метод полягає в наступному: при розрахунках записуємо одну над іншою масові частки розчиненої речовини в початкових розчинах, праворуч між ними - його масову частку в розчині, який потрібно приготувати, і віднімаємо по діагоналі з більшого менше значення. Різниці  таких розрахунків показують масові частки для першого і другого розчинів, необхідні для приготування потрібного розчину.

    4. Розв’язування задач «Методом рибки»  або методом Магницького.                                                                                                                                                               Вперше   такий спосіб вирішення завдань був описаний в арифметиці 18 століття, автором якої був чудовий російський математик і педагог Леонтій Пилипович Магницький. При  розв’язуванні задач цим способом будується схема, схожа на рибку, ось тому він так і називається. Метод полягає в наступному: один під одним записуємо вмісту речовин наявних розчинів (сумішей, сплавів), ліворуч від них і приблизно посередині - вміст речовини в розчині (в суміші або в сплаві), який повинен вийти після змішування. З'єднуємо написані числа прямими. У кожній парі з більшого числа віднімаємо менше, і результат записуємо в кінці відповідної прямої. Отримані масові частки показують, в якому відношенні треба злити вихідні розчини (суміші, сплави). Записуємо пропорцію і  розв’язуємо її.

Пропонуючи учням різні шляхи розв’язання задач, я даю можливість вибору того способу, який буде зрозумілим і запам’ятається для подальшого використання, а значить створюю ситуацію успіху, віру у власні сили. Звичайно всі способи неможливо вивчити на одному уроці, тому я,  вважаю доцільним, використання сучасних методів навчання, наприклад кейс-урок, на якому можна розглянути й обговорити кілька способів розв’язування задач.

Література та інтернет джерела

1. О.В.Григорович. Формування ключових компетентностей на уроках хімії. https://www.slideshare.net/ippo-kubg/ss-74876188
2. Піскунова Наталія Юріївна Формування математичної компетентності учнів. http://www.eduwiki.uran.net.ua/wiki/index.php?title=Формуваня_математичної_компетентності_учнів&action=edit
3. За що відповідає ліве і праве півкуля головного мозку? http://poradumo.pp.ua/cikave/11723-za-scho-vdpovdaye-lve-prave-pvkulya-golovnogo-mozku.html
4. Мнемотехніка – технологія ефективного засвоєння інформації. https://www.slideshare.net/Aniram11/ss-44458472
5. Немченко Марина Германовна, Нестандартные способы решения задач на смеси и сплавы http://открытыйурок.рф/статьи/614626/
6. Хімія - Комплексна підготовка до зовнішнього незалежного оцінювання.  Розділ І.  Загальна хімія. 6. Суміші речовин. Розчини. http://www.subject.com.ua/chemistry/zno1/69.html
7. Решение задач на смеси и сплавы методом Магницкого. https://multiurok.ru/files/rieshieniie-zadach-na-smiesi-i-splavy-mietodom-mag.html
8. Метод Пирсона в решении задач на смеси и сплавы. https://easyen.ru/load/math/ege/metod_pirsona_v_reshenii_zadach_na_smesi_i_splavy/43-1-0-12300